基于探究式教学法的高职数学教学研究——以定积分概念教学为例

朱明娟

（江苏旅游职业学院，江苏 扬州 225000）

《国家中长期教育改革和发展规划纲要（2010—2020 年）》明确提出，创新人才培养模式，深化教育教学改革，创新教育教学方法。倡导启发式、探究式、讨论式、参与式教学，鼓励学生独立思考、自由探索、勇于创新。传统高职数学教学侧重于理论知识灌输，忽略对学生实践能力的培养，导致教学成效不佳。因此，各高职院校应结合高等数学学科特征，引入探究式教学方法，从而更好地培养学生形成科学思维，提高其解决实际问题的能力。

一、探究式教学法分析

（一）基本内涵

探究式教学法以多元智力理论、建构主义理论为基础，强调使学习者通过探究的过程完成知识结构建构，实现思维能力提升以及综合素质发展。将探究式教学法应用于教学领域，要求教师聚焦学科领域与现实生活进行情境创设与问题导入，使学生经由自主思考、调查分析、合作交流等方式开展学习探究活动，并且通过实验操作进行猜想与假设的验证，最终形成科学结论［1］。通过采用探究式教学方法，能够有效激发学生的学习兴趣与自主探究热情，使其在积极的学习态度与氛围中深化学习体验、巩固科学思维、锻炼应用能力，促进学生实践探索与创新思维能力的全面发展［2］。

（二）教学设计步骤

1. 问题导入

探究式教学模式以问题为核心，将学科知识内容与现实生活要素相结合，在学生既有认知与生活经验的基础上创设教学情境，提出具有启发性的问题，吸引学生形成探索意识，并主动参与到探究学习活动中，实现教学目标的顺利导入。

2. 思维探究

在引出探究问题的基础上，由学生基于既有认知经验对问题进行自主分析，初步形成问题解决的思路与方法，随后经由分组讨论、组内交流、集体讨论等方式进行问题分析与猜想假设，完成问题解决与验证方案的初步设计。

3. 问题解决

待提出问题解决方案后，由学生通过探究实践、小组合作等方式进行猜想与假设的验证。此环节主要考查学生团队协作与解决问题的能力。教师可通过适时介入、适当引导帮助学生纠正错误思路、理清思维逻辑，使学生在探究实践中深化学习体验、掌握知识规律、归纳学习方法，最终生成研究结论。

4. 知识建构

教师应指导学生基于既有知识经验与学习能力，将探究学习中生成的研究结论抽象为一般结论，通过回顾整体探究过程，从中提炼出学习经验与解决问题的方法，在实现新知内化的基础上进行自主反思、总结经验，并将所学知识与掌握的学习方法应用于其他问题的解决中，从而进一步拓宽学生的思维向度，完善知识体系建构，提高问题解决能力。

二、探究式教学在定积分概念教学中的具体应用

（一）教学流程实施

1. 创设情境，导入问题

定积分是高等数学微积分学中的重要概念，与微元法、极限思想等数学知识存在一定的关联。通过开展定积分概念教学，能够帮助学生更加直观地领会积分的实质，培养学生形成问题意识与数学思维，提高其分析问题与解决问题的能力。基于此，教师可选取生活化素材进行教学情境的创设，例如，“学校计划在校园内修建一座拱桥，观察拱桥横截面图例可知拱底由左向右分别设有A、B 和E、F 点，桥高为H，拱顶呈抛物线型，桥孔由矩形BCDE 与半径为r 的圆弓组成，沿拱顶顶点向下作垂线与拱桥交于m、n 两点，假设需修建该拱桥的截面墙，所选砌砖的截面长、宽分别为a、b，则求砌筑该桥的截面墙共需应用多少块砖？” 学生在读完题目所给条件后，初步判断该题目为一个简单的初等几何问题，可分别求解出桥和砖的横截面面积，将二者相除即可计算出所需砖的数量，即

砖块数量=（ 抛物线AmF 下部面积- 矩形BCDE 面积- 圆弓CnD 面积）÷（a·b） （1）

但是，依据学生现有初等几何知识无法计算出桥横截面的面积，由此形成问题与学生既有认知经验间的冲突，激发学生的求知欲与探索热情。

2. 提供线索，思维导引

在引出所需解决的问题后，由教师提示学生调动以往所学知识尝试寻求抛物线下方面积的求解方法，学生结合图形对称性特征与坐标系知识，以该抛物线下方图形为基准建立平面直角坐标系，取图形右半部分建立抛物线方程，即

为便于计算，可将L、H 均取值为1，将该抛物线方程简化为：

基于上述步骤，成功将复杂图形面积计算问题转化为求解由抛物线与x、y轴围成的平面图形的面积。接下来，基于平面图形面积的可加性特征，将图形内部划分出若干矩形状竖条，组合构成台阶状图形，从中可看出，竖条划分越细，台阶面积之和越接近抛物线下方面积，因此可通过台阶面积A 的无限细分逼近抛物线下方面积，初步确定问题的解决方案。

3. 探究学习，解决问题

在完成自主思考与探究后，进入合作学习阶段，教师可安排学生开展小组合作学习。在合作学习过程中，教师要在学生协作过程中给予其必要指导，帮助学生顺利解决问题。在计算台阶面积A时，首先应选取某一区间进行面积求解。例如，某小组选择将区间［0，1］进行三等分，以形成的各小区间的右端点为基准，以端点函数值作为矩形高，由此计算出台阶面积的粗糙近似值为：

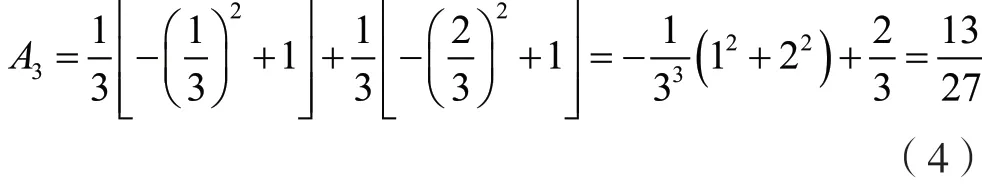
某小组将该区间进行四等分，求得的台阶面积近似值A4优于A3，见式（5）。

在此基础上，教师可启发学生根据上述公式总结规律，假设将区间［0，1］进行n 等分，推导出台阶面积近似值An的计算公式见式（6）。

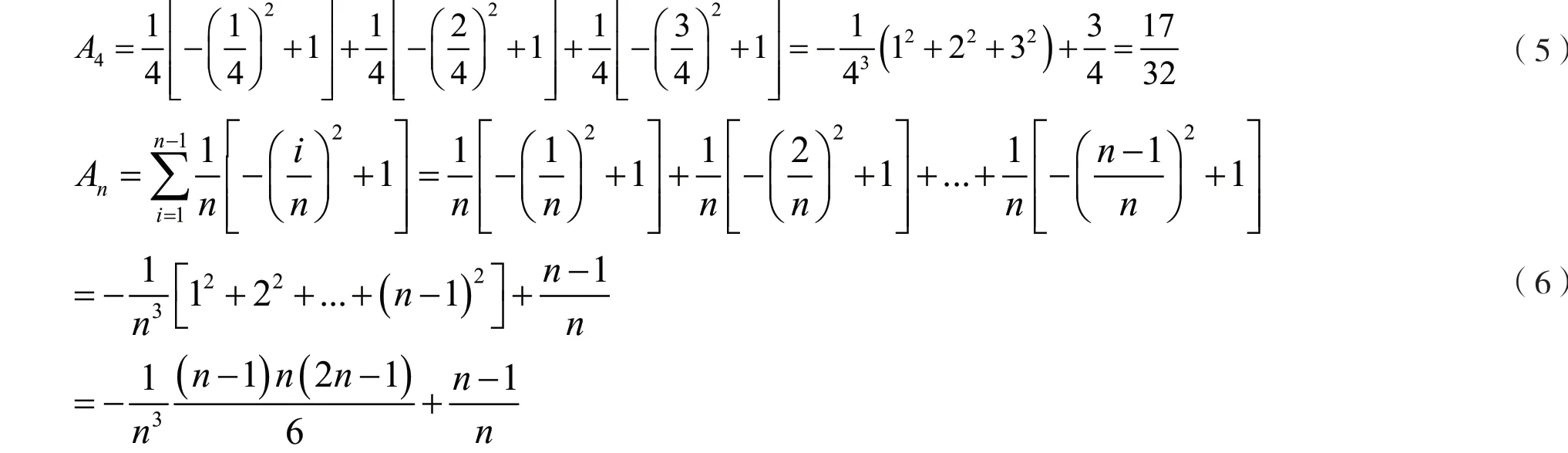
倘若n 相当大，则台阶面积即可无限接近抛物线下方图形面积，由此推导出台阶面积An的极限即抛物线下方图形面积的精确值，由此计算出：

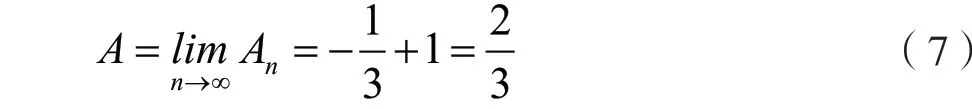
4. 知识总结，拓展延伸

在知识总结环节，由教师带领学生重新梳理探究与推导过程，厘清该问题的解答思路为化整为零—以直线代曲线—积零为整—取极限精确化，即首先基于量化思维将整体量转变为局部量，随后利用平面图形与直线知识在局部量中作近似代替，接下来将局部量的近似值进行整理与累加，最后依据整体量的近似值求解出精确值［3］。在完成思维方法归纳的基础上，教师可引导学生联系实际生活中的问题，运用分割取近似、求和取极限的解题方法解答问题，并且考虑到实际计算的难度与复杂度，需要简化问题解答方法，由此抽象出 “定积分” 的概念，即

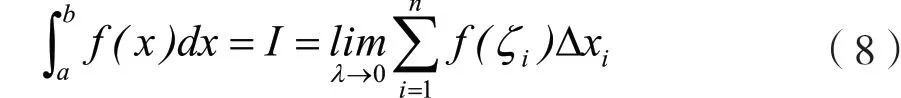
（二）教学模式创新

一方面，教师应利用现代教学手段提供的便捷条件进行教学形式创新，例如，运用多媒体设备将问题求解的过程、推导思路进行动画演示，使学生直观感受分割、近似、求和、取极限的过程与各环节的操作方法，实现抽象概念的直观演绎，进一步增进学生对定积分本质、内涵与思维方法的理解，为实际问题的解决奠定良好基础［4］。另一方面，教师应面向 “互联网+” 教育形势积极引入翻转课堂教学模式，建立“微课+ 探究式学习” 的混合式教学模式，课前，教师在教学平台上发布微课视频资源，引导学生进行自主探究学习，培养其形成良好的学习习惯；课中，教师随机抽选学生围绕学习任务单内容进行汇报，用于检测课前预习成果，并结合学生学习成果发布当堂探究任务，安排学生以自主探究、小组合作等方式开展学习活动，并基于Mathematical 等软件进行实操演练；课后，教师可安排学生结合本专业知识进行拓展练习，例如，针对建筑工程专业学生，可为其安排隧道施工中开挖出的土石量计算这一学习任务，以此考查学生将所学概念应用于解决实际问题的能力。

（三）教学效果评价

在完成教学设计的基础上，为检验学生的学习成效，教师可为学生布置课后练习测试，将测试结果与学生课前预习、自主探究及小组合作等学习结果相结合，生成综合评价结果，并且引导学生进行问题归纳与自主反思。同时，教师要结合学情分析与练习测试结果总结教学经验，弥补探究式教学实施过程中存在的缺陷，更好地提升教学质量与效率，实现对学生知识结构、数学思维与探究能力的有效培育。

结语

当前高职院校生源结构呈现出多样化特征，学科体系、课时安排的变化均使教学难度增大。定积分概念与微元法、极限思想方法等知识存在密切关联，对学生思维能力的培养具有重要意义。因此，教师需对探究式教学法的流程、方法进行优化设计，以有效培养学生问题意识和解决问题的能力。