铁路快运班列开行方案与车底周转一体化优化研究
李新毅,李海鹰,王 莹,廖正文,,苗建瑞
(1.北京交通大学 交通运输学院,北京 100044; 2.中国铁路设计集团有限公司 线路站场枢纽设计研究院,天津 300308;3.北京交通大学 轨道交通控制与安全国家重点实验室,北京 100044)
铁路快运班列是在固定发到站间,有固定运行线和确定运行周期的一种货运产品,服务对象以高时效、小批量的快捷运输需求为主。随着铁路市场化进程的加快与既有线运能的释放,铁路部门采取直达、中转、循环等相结合的班列组织方式,以有效利用运输能力,提高班列服务水平。差异化的开行模式,使得运输组织工作日趋复杂。此外,车底是班列开行方案兑现质量的保障,而货运的快速化需求对列车提出了运行高速化和装卸便捷化的要求,导致可供运用的车底资源呈现出紧缺状态。如何同步实现开行方案的合理编制与车底资源的高效周转,成为值得研究的问题。
班列开行方案是在尽可能满足货物运输需求的基础上,科学合理地安排班列的起讫站点、运行径路、编组内容、开行频率等,实现从货流到车流再到列流的组织方案[1]。班列的车底周转计划则用于指派各车底承担相应的班列运行任务,以实现车底的合理循环运用。专家学者对以上两个问题进行了深入研究,在优化班列开行方案时,或考虑不同因素直接构建优化模型[2-4]或基于服务网络构建网络流模型[5-7];对于车底周转计划的优化,主要将问题抽象为旅行商问题和指派问题[8-10]。上述研究通常将开行方案与车底周转两个问题割裂考虑,打破了顶层计划与底层资源的关联,使得优化结果具有局限性。班列开行方案是通过匹配货物运输需求与铁路运力资源,实现“组流上线”的运输计划,其计划质量决定运营收入,车底周转计划则是在开行方案的基本框架下,给出移动运力资源在时间和空间上的配置方案,该方案决定开行方案的兑现成本。如果能够在决策阶段考虑二者的一体化优化,既可以实现铁路部门降本增效,又可以保障班列的顺畅组织,同时其优化结果可为确定班列运行线提供有效参考。
近年来,也有学者利用服务网络设计方法对上述两个问题的一体化优化展开了研究,通过将时间维度引入服务网络来刻画车底的周转运用,使原问题转化为一类网络设计问题[11-15]。文献[11-12]研究了考虑多资源周转的开行方案优化问题,分别构建了点-弧和弧-路网络流模型,目标是最小化货物运输成本。文献[13]在文献[11-12]的基础上,提出一种分支-定价的求解框架,提高了模型的求解效率。文献[14]将原问题拆分为服务网络构建、货物流量分配、车辆运用安排3个阶段,并设计了面向大规模案例的求解算法。文献[15]对考虑车辆周转的铁路动态货运服务网络设计问题进行研究,构建了基于路径的多商品网络流模型,并给出一种分支-定价-切割的求解算法。但是既有研究往往为降低求解难度而增大时间离散精度,不利于对车底接续、货流中转等作业环节的刻画,优化结果难以应用于实际。
本文针对班列开行方案与车底周转一体化优化问题,引入“运输状态”维度,建立“时间-空间-状态”服务网络,将原问题转化为考虑车底周转的服务网络设计问题。货物的运输过程和车底的运用安排可看作货物与车底在服务网络中的流动过程,即所谓货流和车辆流,车底资源与货运需求以服务网络为媒介实现供给与需求的匹配。基于此构建0-1整数规划优化模型,设计基于拉格朗日松弛算法的快速求解框架,并通过算例对模型和算法的求解效率和优化质量进行验证。
1 “时间-空间-状态”服务网络的构建
考虑图1所示的铁路物理网络。将车站抽象为车站节点,在时间轴上将车站节点按照单位时段拓展离散,在空间轴上将车站节点进一步拆分为到达节点和出发节点。引入“运输状态”维度L={l1,l2,…,lmax},L中元素为为货物和车底的“运输状态”。对于货物而言,运输状态是指货物当前所装载的班列;对于车底而言,运输状态是指车底当前所担当的班列。基于此构建“时间-空间-状态”服务网络G=(N,A),其中:N为节点集合;Na、Nd分别为车站的到达节点和出发节点集合,表示班列的到发作业,Na、Nd∈N;Nv为虚拟节点集合,表示货流和车辆流在网络中的逻辑起点与终点,Nv∈N;A为节点间的有向弧集合,包括运行弧集合As∈A、停站弧集合Ae∈A、中转弧集合At∈A、接续弧集合Ac∈A和虚拟弧集合Av∈A,其中,运行弧和停站弧是班列的组成部分,分别表示班列的区间运行过程和停站作业过程,中转弧和接续弧穿插于不同的运输状态维度,通过运输状态的变化表示货物在班列间的中转过程和车底在班列间的接续过程,虚拟弧无实际含义,仅用于描述货流和车辆流在网络中的生成与消失。

图1 铁路物理网络
在构建时空状态服务网络时,根据货流的出发时间窗和货物的运到时限给出货物的到达时间窗,然后生成所有符合时间窗约束的虚拟弧,并根据货流的最小中转时间生成所有符合中转时间约束的中转弧,从而保证服务网络中所有可能被选择的服务路径均满足上述关于时效性的约束。图2为时空状态服务网络的示意图,图中,一支发到站分别为TA站和TD站的货流,首先在班列l1的运行弧集合中选择一条弧段,实现由TA至TB的站间运输,然后经由合适的中转弧进行运输状态的转换,从而实现货流从班列l1中转至班列l2,货流从TB站至TD站的运输作业将由班列l2完成,通过班列l1、l2及一次货流中转,实现从TA站至TD站的运输。类似的,通过对运行弧、停站弧和接续弧进行选择组合也可刻画车辆流的周转过程。在上述货流和车辆流的流动过程中,车辆流是弧段运输能力的供给方,而货流则是弧段运输能力的消耗方,通过约束货流与车辆流在服务网络中的时空一致性,得到车底资源与货运需求的供需匹配结果,即获得班列的出发和到达时刻、运行径路、货流的分配方案以及车底的接续方案等信息,从而确定班列开行方案和车底周转计划。
相比于传统动态服务网络,此种网络构建方式虽然在一定程度上扩大了网络规模,但可实现货物中转、车底接续与班列停站的差异化表达,有助于清晰刻画车底和货物在时间和空间上的周转过程。

图2 “时间-空间-状态”服务网络示意图
2 铁路快运班列开行方案与车底周转一体化优化模型
2.1 模型假设
(1)能力假设。不考虑线路的区间通过能力瓶颈;各车站的作业能力能够满足班列到发、货物装卸、中转和车底接续的作业要求。
(2)货运需求不固定。班列是否开行取决于运输收益,满足货运需求仅作为软约束,对未能通过班列运输的货流,可由普通列车运输完成。
(3)车底固定编组、固定区段运行。班列运行中无车辆甩挂、解编作业,货物装卸依靠集装化器具和快速化机械设备完成。
2.2 符号定义
(1)集合与元素
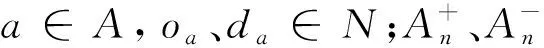
V为车辆流(车底)集合,v∈V;ov、dv分别为车辆流v的始发、终到节点,ov、dv∈Nv;Tv为车底v的编成辆数(车辆流流量)。
(2)参数
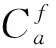
(3)决策变量

2.3 模型构建
以最大化铁路部门运营收益为优化目标,模型目标函数为
(1)
s.t.
(2)
式(2)为货流流量约束,该约束保证被服务的流量之和小于等于总的货流流量。按照模型假设(2)的描述,约束取小于等于而非等于。
(3)
式(3)为货流的流平衡约束,货流是否分配至弧段a∈A以0-1变量的形式体现,从而确保各支货流在唯一空间路径上不可拆分。
(4)
式(4)为车辆流的流平衡约束,车辆流是否流经弧段a∈A以0-1变量的形式体现,从而确保车辆流在唯一空间路径上不可解编。
(5)
式(5)为车底运用数量约束,表示投入运用的车底数量必须小于或等于可供运用的车底数量。
(6)
式(6)为车底指派约束,该约束保证任一班列任务仅与唯一车底存在指派关系。
(7)
式(7)为弧段运输能力约束,该约束体现了车底与货流的供需关系,即车底为弧段提供的运输能力须大于其上货流流量。
(8)
(9)
式(8)、式(9)表示决策变量的取值范围约束。
上述模型为0-1整数规划模型,模型约束和决策变量规模与时空状态网络的弧段规模相对应。动态服务网络经过时空维度的节点离散后,弧段规模较大,使用商用优化求解器难以在可接受时间内获取最优解,而本文在动态服务网络的基础上又进行了状态维度的拓展,模型的求解难度更高,故给出基于拉格朗日松弛的求解算法,通过松弛强耦合约束,使原问题分解为货流分配和车底周转两类结构简单的子问题,实现大规模问题的分而治之。
3 基于拉格朗日松弛的启发式算法
3.1 拉格朗日对偶问题的构造
本文优化模型求解的困难之处在于货流分配和车底周转之间的强耦合性。因此在采用拉格朗日松弛算法时,我们将弧段运输能力约束(式(7))和车底指派约束(式(6))松弛,在目标函数中引入拉格朗日乘子惩罚项,构造拉格朗日松弛问题,为
(10)
式中:ρa、σa为拉格朗日乘子。
式(10)为利润最大化问题可进一步等价变换为成本最小化问题即
(11)
式(11)中L(ρ,σ)的目标值对应模型的下界值,为获取模型的最大下界,我们构造拉格朗日对偶问题L(D),目标函数为
L(D)=maxL(ρ,σ)
s.t.
式(2)~式(5)、式(8)、式(9)
(12)
拉格朗日对偶问题通过在松弛约束中添加新的变量(拉格朗日乘子),使得两类子问题的耦合关系打开,因此新的整数问题分解为一类经典的运筹学优化问题——最小费用路径问题。通过逐一构建符合货流和车辆流约束条件的服务网络,即可借助最短路算法快速求得对偶问题的可行解。
3.2 获得可行解的启发式算法
由于部分约束被松弛,因此求解拉格朗日对偶问题得到的下界解可能为非可行解,需要针对该问题设计启发式算法。该算法将下界中的车辆流和货流在服务网络中的路径信息作为启发信息,按照一定的顺序逐一规划各车辆流和货流,从而求得可行解。
m、n分别为车辆流和货流编号,弧段运输能力为Ccap。基于松弛问题解得到可行解的步骤如下:
Step1初始化。令m=0,n=0,对∀a∈A,令Ccap=0。
Step2加载车辆流。令m=m+1,若m>R,进入Step4;提取下界解中第m支车辆流的周转路径,遍历路径中弧段的车底占用标记,若已被占用,转至Step3,否则令弧段Ccap=Tm(Tm为车辆流m的流量大小),继续Step2。
Step3车底周转的可行化。将服务网络中已被指派车底的弧段剔除;更新车辆流m的最小费用径路,转至Step2。
Step4确定货流规划优先级。对∀f∈F,其规划优先级系数ψf为
μ+ω=1μ,ω∈[0,1]
(13)
式中:Hf为货流f∈F的路径费用。
取μ=0.2,ω=0.8,ψf值越大表明服务该货流的收益越高。
Step5加载货流。按照ψf由大至小顺序更新货流编号n。令n=n+1,若n>P(P为待服务货流数量),进入Step7;加载第n支货流至服务网络。遍历货流路径中弧段,若存在弧段其Ccap Step6货流分配的可行化。将服务网络中Ccap Step7保存可行解,计算原问题上界,算法结束。 在给定的拉格朗日乘子下,我们可以获得拉格朗日对偶问题的一个下界解,在求解时,通过对拉格朗日乘子值进行迭代更新,使下界解逐步逼近最优解。拉格朗日乘子的次梯度更新方法为 (14) (15) 式中:k为迭代次数;δ为迭代步长,δk=1/k+1。 式(14)、式(15)中,拉格朗日乘子ρa是当供需不平衡时产生的“惩罚费用”,反映了弧段运输能力与其上货流流量的适应程度,而σa可以理解为弧段这一时空资源的“占用价格”,即车辆流占用弧段的代价。次梯度法是根据车辆流和货流的弧段占用信息,对“惩罚费用”与“占用价格”迭代更新,实现弧段资源的动态定价,继而影响货流与车辆流在下次迭代中的路径选择。通过对“资源定价”与“路径选择”过程的反复迭代[16],最终得到货流需求与车底资源的最佳时空映射关系。 Step2拉格朗日对偶子问题的求解。 Step5以3.3节所述方法更新拉格朗日乘子ρa、σa。 Step6终止条件检验。如果迭代次数k大于预设的最大迭代次数则算法终止;否则k=k+1,转至Step2。 以包含8座车站的铁路路网作为算例对模型和算法进行验证,见图3。用C#语言编写拉格朗日松弛启发式算法的计算程序,程序运行环境为Intel(R)Core(TM)i5-3470 3.2 GHz,4.00 GB内存的台式计算机。在该算例中,以3 d作为决策周期,时空状态服务网络时间离散化的精度设为1 h,站间距离以区间运行时间的形式表示,均为单位时间长度的整数倍,并在图中进行了标注。 图3 铁路路网拓扑结构 (1)货流数据见表1。 表1 货流信息 关于货流的到发时间窗,本文在考虑货物的运到时限的同时,还结合了货主的接取送达时间以给出更符合实际的到发时间窗。由于时空状态服务网络中包含时间属性,因此在网络构建时,可根据货流的到发时间窗生成可能的虚拟弧段,货流的出发和到达作业均通过访问以上虚拟弧段实现,从而既保证货物的运到时限又满足货主在接取送达时间上的要求。货流的最小中转时间设定为2 h,以保证车站运输组织工作顺利进行。 (2)车底数据见表2。 表2 车底信息 车底的起讫节点按照其始发站抽象为服务网络中的虚拟节点。车底的最小接续时间设定为4 h。 在本算例中,货流和车辆流通过运行弧和停站弧的价格均为固定的时间成本(1元/(车·h)),中转弧价格为50元/车。此外,不考虑虚拟弧、停站弧和中转弧的能力限制。 (3)班列备选集数据。由于服务网络引入了状态维度,因此须事先给出班列的可选集合。在本算例中,不考虑各运输区段的通过能力,货流均可通过最短路径满足运输需求,因此班列备选集通过最短路算法给出。具体方法是,在图3所示的铁路物理网络中,以每一个货流OD需求为输入,借助最短路算法生成各OD对之间的运行径路。在此基础上,遵循车底周转循环的原则确定班列的运行径路,并以此作为班列的备选集。 (4)其他参数。货流的运输成本与收入在货流由起点出发访问相应虚拟弧时产生,即货流被服务则产生以上收益;与班列开行相关的线路使用费和开行成本等在车辆流访问相应虚拟弧和接续弧时产生,即车底选择执行班列任务时需付出以上费用。其他参数取值见表3。 表3 其他参数取值 利用拉格朗日松弛算法进行300次迭代,对上述算例进行测算,总耗时81.5 s,最优目标函数值为2 428 651.36元。班列开行方案和车底周转计划见表4、表5。 表4 班列开行方案 表5 车底周转计划 由表4可知,优化方案开行班列总数为11,其中有6列为一站直达班列,在剩余5列停站班列中有两列班列间存在货流的中转关系(班列6与班列10)。在上述班列中,执行班列3、4、5运输任务的车底为同一车底(见表5“担当班列”),可组合为循环班列,剩余8对班列组成往返对开班列。在20支货流中,货流7和货流15未被运输,这说明服务上述小股货流将出现返程班列回空现象,导致运营亏损,因此予以舍弃。 由表5可知,在决策周期内,各车底的起讫车站相同,表明车底以固定区段的方式循环周转。算例共使用5组车底,两组车底未被运用,原因是车底空车走行的成本高,而剩余小股货流不足以组织对开班列。 在上述算例中,如果设定仅可开行直达班列,经算法测试,最优目标函数值降低为1 984 161.52元。班列总数依然为11列,但未被运输货流数量变为9支,多为小批量货流,分别为货流3、4、7、10、13、14、15、16、18,这表明本文优化方法可以根据货流特点,通过组织开行适当数量的停站班列,以有效吸引小股货流,实现铁路运营收益的最大化;考虑到中转班列的作业复杂,如果假设按照直达和停站班列结合的模式组织运输,不开行中转班列,则共开行班列11列,货流10(H—E)未被运输,目标函数值降低为2 358 196.56元。 进一步地,维持原有算例的数据集不变,减少可供运用的车底数量,保留车底1、2、3、6,班列开行总数变为9列,车底6的担当班列变为班列8(A—G)和班列9(G—A),班列10(A—E)和班列11(E—A)停开,共有7支货流未被运输,最优目标函数值降低为2 127 834.32元。 本文研究了铁路快运班列开行方案与车底周转的一体化优化问题,为实现货物运输与车底周转过程的清晰表达,在传统动态服务网络中引入运输状态维度,构建了“时间-空间-状态”服务网络,并据此构建了考虑货流中转和车底接续的网络流模型。文中给出一种基于拉格朗日松弛的启发式求解算法,在相同算例数据集下的灵敏度分析验证了模型与算法的有效性。结果表明,本文提出的优化方法不仅可以基于货流特点与组织方式给出收益最佳的班列开行方案,还可以实现班列开行方案和车底周转计划在不同车底资源配置场景下的一体化优化调整。在算例求解时,班列开行备选集的完备性与合理性对优化结果有一定影响,对于班列备选集的生成策略尚待进一步完善。3.3 拉格朗日乘子的更新方法
3.4 算法流程


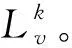

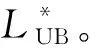
4 算例分析




5 结论

