基于时间连续性的企业枢纽车站进路选择优化
郑开娣,查伟雄,王 敏,严利鑫
(1.国科大杭州高等研究院,浙江 杭州 310024;2.华东交通大学 交通运输与物流学院,江西 南昌 330013;3.合肥市轨道交通集团有限公司,安徽 合肥 230001)
列车进路的选择排列是车站作业组织的关键,企业铁路大型集配枢纽站列车到发密集、车流集中、车站设备资源使用强度高,其线路结构及作业方式较普速铁路车站更为复杂。有针对性地探究企业车站作业进路安排对提高企业车站的运输能力与运输效率有重要意义和实用价值,许多学者进行了相关研究:Corman等[1]通过调整列车停站时间、列车速度、进站顺序及进路分配等,以最小化列车延误时间为目标动态调整车站作业计划;Lusby等[2]将列车可行进路排列问题转化为可行进路数最大化的节点压缩模型;Gao等[3]通过合理安排作业进路增强列车作业的强壮性,降低客运行车作业中扰动造成晚点传播的强度和范围;郭彬等[4]以作业链描述并优化车站作业,减少列车进路冲突、提高作业鲁棒性;史峰等[5]、陈彦等[6]以道岔和到发线占用相容性为约束,以最大化接发车作业进路效用和到发线运用效用为优化目标,建立旅客列车过站径路优化的0-1规划模型;雷定猷等[7]运用多目标规划理论将优化目标分解为方便旅客旅行、有利于保证行车作业安全与行车技术作业和有效地使用车站各种既有行车技术设备等3个子目标,并分别建立优化模型;赵鹏等[8]将到发线和咽喉区作为整体进行综合优化;马驷等[9]在将到发线和咽喉区作为整体优化的基础上考虑列车晚点情况,以车站作业过程占用车站设备的不均衡性最小和列车进站延误时间最短为目标,建立列车进路分配方案的动态调整模型;龙建成等[10]以作业晚点时间最短以及各进路的总走行时间最短为目标,构建车站进路选择模型,并将其转化为等价的0-1整数规划模型。既有研究多针对高速铁路车站行车作业进路及咽喉区进路选择排列[11-14],对调车作业进路选择排列及企业铁路车站进路选择排列研究较少。
企业枢纽车站调车作业远多于行车作业,而调车作业反复占用咽喉道岔对咽喉区的影响较大。调车作业具有不同于行车作业的特殊性,车站作业一般要求调车作业尽可能连续完成,即在作业计划确定的前提下调车作业的进路选择排列具有时间连续性,这也是既有文献中没有考虑的。本文基于时间连续性建立冲突产生延误时间最小及走行时间最少的多目标函数模型,考虑以进路交叉冲突产生的延误时间来衡量进路冲突对原定连续作业的调车作业时间连续性的破坏程度,优化调车作业的进路选择排列,提高企业枢纽车站的通过能力和作业效率。
1 企业铁路枢纽站作业特点
企业铁路车站与普速、高速铁路车站在车站到发作业以及进路冲突疏解等问题上基本相同。但由于企业铁路车站只有货物运输,以及企业生产等实际需求,企业铁路枢纽站具有一些新的特性。
(1)行车组织复杂
企业铁路建成时间较早,为了运输和装卸方便,大多数线路有多个用途,例如某条线路既为走行线和交接线,同时由于与作业车间连接,又必须进行装卸作业。同时,企业铁路枢纽站的道岔较多、特种车辆多、运行区域和货物基本固定,而且极易受生产调整的影响。企业到发列车时间有一定的规律,车流和货物信息可以预报,涉及的生产部门较多。
(2)行车作业与调车作业并存
企业铁路枢纽站需要进行小运转列车的到发编解作业以及取送车作业,作业较为密集,始发、终到列车易与调车作业在车站咽喉区产生进路交叉冲突。企业铁路枢纽站调车作业与行车作业的交叉干扰,加深了咽喉区道岔的负荷,同时也制约着车站通过能力的提升。
(3)调车作业多
由于区域的限制及企业生产的需要,企业铁路枢纽站涵盖了接发列车作业、列车的解体和编组作业、向装卸区取送车作业、列车及车辆的技术检查作业、特种运输车辆的组织和机车的整备作业等几乎所有的技术作业类型。车站货物运输作业所占比重较大,取送作业量大且频繁,导致企业铁路运输系统更加繁忙和复杂。频繁的调车作业大大增加了车站咽喉区的压力。对于确定作业计划的调车作业,其进路选择排列在时空范围上是一个动态的过程,且调车作业的进路选择排列具有时间连续性,即要求车站作业尽可能连续完成,前项作业完成情况直接影响后续作业的完成,因此必须考虑前后项作业的接续。
针对企业枢纽站的以上特点,建立进路选择优化模型,在多种类作业并存情况下确保行车作业优先,同时为调车作业分配能够最大程度上保持其时间连续性的合理进路,为企业枢纽站的进路安排现场工作提供合理有效的解决方案。
2 模型构建
将道岔组、站线、衔接方向作为网络节点,按照道岔分组规则[9],构建车站拓扑结构图。(k,k+1)为节点k、k+1之间连接弧,弧均为双向弧;作业进路以节点的有序集合表示,如(k-1,k,k+1)。
2.1 约束条件
(1)Is为企业铁路枢纽站调车作业集合;Ir为行车作业集合;Di为作业i可用的进路集合。
(1)
(2)
式中:xij为0-1决策变量,若调车作业i占用进路j则xij=1,否则xij=0;yij为0-1决策变量,若行车作业i占用进路j则yij=1,否则yij=0。
式(1)、式(2)表示每项作业排列进路时,必须选定该项作业可用进路集合中的一条,且只占用其中一条。特别地,行车作业的可用进路必须为正线进路。
(2)计算各项作业选定的进路对途经节点的计划占用时间。
进路j占用节点k的情况见图1,节点占用时刻为
(3)
(4)


图1 节点时间占用示意
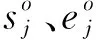
(5)
(6)
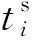
对于作业终点节点d,其占用结束时刻为
(7)
(8)
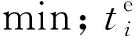
对于调车作业,一个调车作业单有数钩作业,在进行进路安排时需要按钩分解成多个依次进行的分项作业,对各分项作业依次选择进路后形成调车作业单的进路方案。设有两分项作业i1、i2,H为相邻分项作业的集合,若(i1,i2)∈H,则后项作业i2的开始时刻为前项作业i1结束时刻加上两作业间隔时间,即
(9)
式中:t(wi1,wi2)为两项作业的安全间隔时间,min;wi为不同类型作业的权重,设置权重时,一般行车作业的赋值大于调车作业,接车作业的赋值大于发车作业。由作业权重判断两项作业的类型以决定其安全间隔时间的取值。按照提前10 min停止影响接车进路的调车作业、提前5 min停止影响发车进路的调车作业、后一作业待前一作业结束后间隔1 min再开始的原则,确定t(wi1,wi2)的取值。
(3)根据节点占用时间判断是否存在进路交叉冲突。
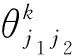
∀k∈Zj1∩Zj2
(10)
(4)当两进路在某一节点冲突时,需要对这两条进路在时间上进行疏解。
若为调车作业进路与行车作业进路冲突,行车作业直接通过无延误,调车作业需中断,待行车作业进路占用冲突节点结束后继续进行,调车作业产生的延误时间为
∀k∈Zj1∩Zj2
(11)
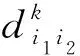
该约束能够在进路排列时确保行车作业严格按照运行时刻表完成。
若为两调车作业的进路相冲突,则开始时间较迟的调车作业需要中断等待,作业中断造成的延误时间为
(12)
经时间疏解的进路j1在冲突节点k处的占用开始和结束时间需重新计算。即
(13)
(14)
因车辆在冲突节点k的前一节点k-1处等待,故节点k-1的占用结束时间更新为
(15)
并且该进路中的后续节点占用时间,以及该项作业的后续作业的节点占用时间,都需按式(3)~式(9)重新确定。
2.2 目标函数
进路选择优化问题是一个具有空间和时间二维特性的组合优化问题,基于时间连续性,目标函数的构建从以下两个方面考虑:
(1)进路冲突产生的延误时间最小。调车连续作业的条件下,考虑以交叉冲突产生的延误时间来衡量进路冲突对调车作业的时间连续性的破坏程度,冲突产生延误时间越小,则调车作业的时间连续性越好。调车作业的时间连续性指:在现场作业中作业人员倾向于为调车作业选择能够连续作业的进路,避免因与其他调车作业或行车作业产生交叉冲突而导致该项调车作业中断等待并影响后续作业的进行。当无进路冲突时各分项作业节点占用时间紧密衔接,当存在进路冲突情况时等待延误时间最小,求解模型得到的进路能够在时间安排上最大程度保证作业的时间连续性。故有目标函数
(16)
(2)各项作业的总走行时间最短。除保障调车作业的时间连续性外,进路方案的走行时间亦尽可能短为宜,因此以走行时间最短为模型的第二个目标函数
(17)
采用线性加权求和的方法,将多目标转化为单目标,即
minf=p1·f1+p2·f2
(18)
p1、p2的取值决定了选择进路方案时延误时间与走行时间的侧重关系,可根据需要进行调整。
3 模型求解
车站作业有固定的特殊要求,并不是所有进路都能满足。针对此问题,首先建立基本进路表,基于基本进路表产生初始解。基本进路表包含每项作业可选的所有可行进路,是后续安排车站作业进路的基础。再根据模型特点设计遗传算法求解。
3.1 构建基本进路表
V为节点集合,k∈V;E为弧集合,(k,k+1)∈E;A为待搜索的不完整进路集合,a∈A;R为从o到d的进路集合,r∈R,|R|为R中的元素个数(即可行进路数量)。
作业可使用的基本进路表生成方法流程见图2。
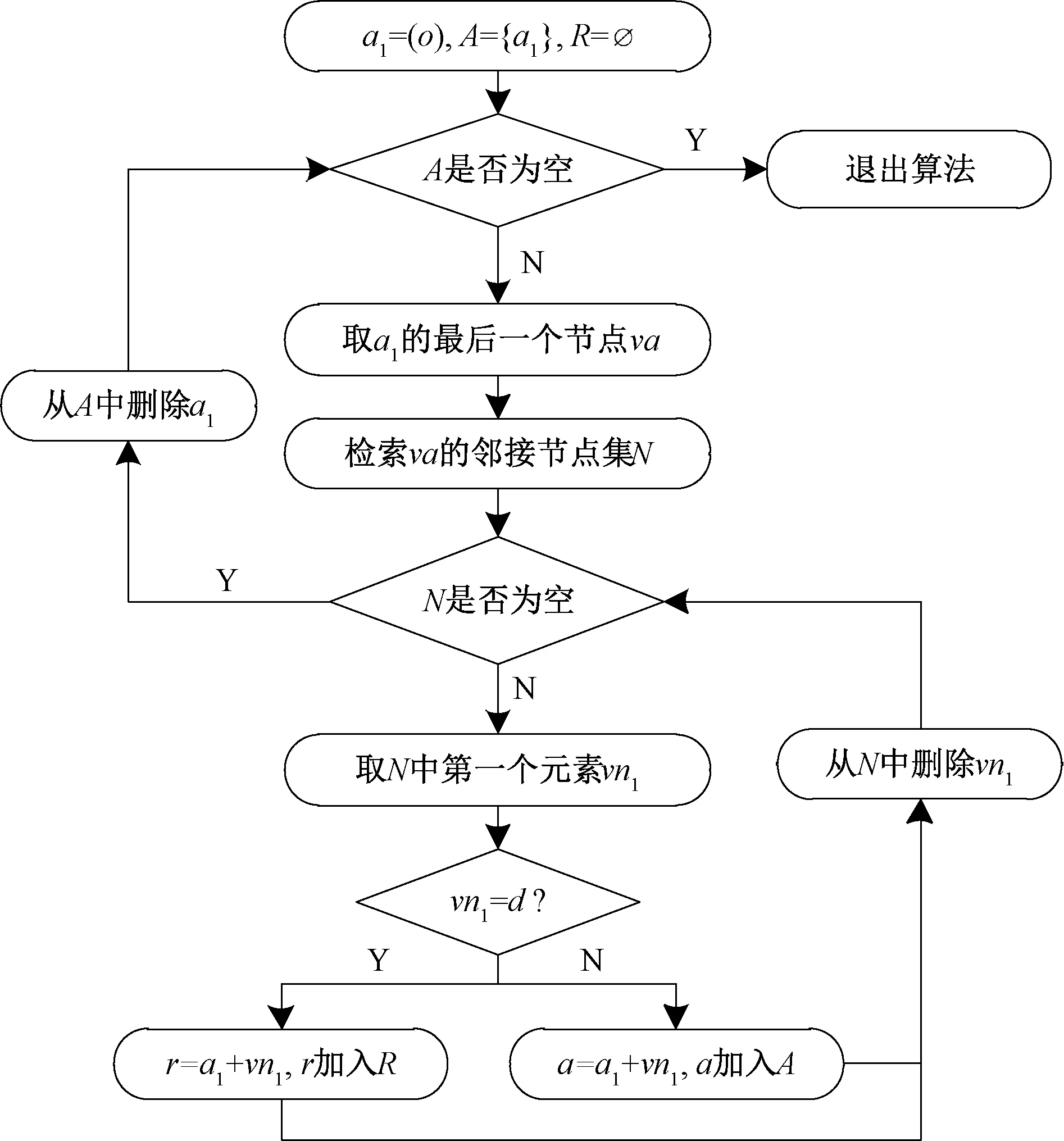
图2 基本进路表生成流程
3.2 求解算法设计
设计遗传算法求解本文构建的进路优化选择模型。遗传算法的适应度函数设计为总目标函数的倒数,即个体ci总目标函数值越小则其适应度越高,即
(19)
个体编码方案采取自然数编码,染色体长度llength=|I|·n,|I|为作业总数,n为站场拓扑图节点总数。每一长度为n的基因片段代表着相应作业的进路,片段中每一个基因的取值为进路按序经过的拓扑图中节点的编号(终节点后的基因取0)。
遗传算法求解步骤为
Step1按前文所述,生成各项作业的基本进路表。
Step2对于调车作业,在其基本进路表中随机选择一条可行进路;对于行车作业,选择一条正线进路。按编码方法转码为初始染色体个体。
Step3重复Step2M(种群数目)次,生成初始种群,进化代数g=0,全局最大适应度gbest=0。
Step4计算各个体适应度函数值。对于每一个体,按作业次序及节点占用次序,由式(3)~式(9)依次计算节点占用时间;随后根据式(10)判断是否存在节点占用冲突(即进路交叉),若存在,则按式(11)~式(15)从占用时间上进行疏解并记录延误时间,最后再次由式(3)~式(9)更新节点占用时间;循环这一判断节点占用冲突、时间疏解、更新节点占用时间的过程,直至无节点占用冲突,得到最终累计的延误总时间(即目标函数值f1);计算该个体方案的总走行时间(即目标函数值f2),最终按式(18)、式(19)得到适应度函数值。
Step5比较个体适应度函数值,将其中适应度最大的个体作为精英解保留至第g+1代;若有个体i其适应度ffitness(ci)>gbest,令gbest=ffitness(ci),并将个体ci保存为全局最优个体。
Step6轮盘赌选择的方法选出M-1个个体。
Step7交叉操作。随机选择两个体作为交叉个体,随机选择某两项作业对应的基因位置作为双点交叉位置,生成[0,1]区间内随机数r1,若r1 Step8变异操作。随机选择一个体,生成[0,1]区间内随机数r2,若r2 Step9若g 本文以某一实际企业铁路枢纽站为例,该站由于生产需要,运输任务重,线路利用率高,车流较为复杂。其中Ⅲ场是该站目前调车作业量最大,接发列车对数最多的场区,连接了6个方向,各方向到发车辆混杂,行车作业和调车作业频繁。 依据道岔分组原则,构建Ⅲ场的网络拓扑图,见图3,图中:Dl为每一个道岔组作为枢纽站网络拓扑图的节点;Sb为每一条站线作为枢纽站网络拓扑图节点;Zc为车站正线的衔接方向节点;Qh为其他的衔接方向节点;l、b、c、h为节点编号。连接弧的走行时间见表1。 待安排调车作业1将原本4钩的调车作业计划单,按照调车必经的起终节点进行细化拆分成9项分项作业,见表2。其中,调车作业1的首项分项作业1.1的开始时刻为10:09,后续作业2.1~5.2依次进行。同样地,待安排调车作业2将原本5钩的调车作业计划单,按照调车必经的起终节点进行细化拆分成13项分项作业,其首项分项作业1.1的开始时刻为10:20,见表3。另有发车作业3,其起点节点为Z5,终点节点为Z2,开始时刻为10:05;发车作业4,其起点节点为Z1,终点节点为Z4,开始时刻为10:32。 图3 Ⅲ场网络拓扑图 表1 站场拓扑图连接弧走行时间 min 表2 待安排调车作业1(开始时刻10:09) 表3 待安排调车作业2(开始时刻10:20) 采用Matlab按本文所设计算法编写程序求解,遗传算法种群数目取值50,能够保持种群多样性及收敛速度。由于可能的进路组合(即可能解)规模较大,需要较大的交叉和变异系数,有利于跳出局部优解,交叉系数取0.8,变异系数取0.2。经多次测算,即使在不同的p1、p2取值情况下,算法一般在200代内都能够收敛,故最大进化代数取300代。 分析不同的p1、p2取值情况下,求解模型得到的进路方案之间的差异。 (1)p1=0,p2=1,即忽略时间连续性,以走行时间最短为目标。程序运行至第124代取得最优解,收敛过程见图4,最优进路方案见表4。该方案走行时间为95.5 min,延误时间为48 min。 (2)p1=0.6,p2=0.4,即略偏重于时间连续性,同时兼顾考虑走行时间的进路方案。由于从车站作业安全管理角度要求车站作业尽可能连续完成,故现场调度员更倾向于在适度延长走行时间的情况下能够减少等待延误时间的进路方案,以提高作业的时间连续性,使作业组织更加有序。因此采用p1=0.6,p2=0.4的系数设置进行计算,其他程序参数同上。程序运行至第172代取得最优解,收敛过程见图4,最优进路方案如表4中所示。该方案走行时间为125 min,延误时间为4.2 min,总目标函数值为52.52。方案1在此种系数设置的情况下,总目标函数值为67,方案2较方案1优化幅度达到21.6%。 方案1中,各分项作业均选择走行时间最短的进路,但调车作业1持续占用咽喉道岔节点D23、D37导致了大量进路冲突、产生了大量延误时间,对调车作业1的时间连续性造成很大破坏。方案2中,调车作业1的分项作业1、3、9选择了走行时间较长的进路,但由此大量减少了与发车作业4、调车作业2的冲突延误时间。调车作业2的分项作业10、15、16亦选择了走行时间较长的进路,规避了与其他作业的冲突。 两个方案均确保了发车作业沿正线进路按运行时刻表准时运行。考虑时间连续性的方案2较未考虑时间连续性的方案1优化幅度达到21.6%,且大大改善了调车作业的时间连续性,调车作业更加流畅有序。 模型对进路冲突的时间疏解,以方案2为例,发车分项作业24占用节点D23的时间段为10:33:48—10:35:18,占用节点D37的时间段为10:34:24—10:37:06。分项作业3、4的进路占用部分节点的开始和结束时刻见表5,分项作业3在节点D23处的计划占用时间段为10:33:54—10:34:06,与发车分项作业24占用节点D23的时间相冲突,故在区段D31~D25等待。发车分项作业24于10:35:18占用节点D23结束,经过耗时1 min的进路申请、确认及开放过程后,分项作业3于10:35:18开始占用节点D23,至10:36:30占用结束,相较于原计划延误了2.4 min。分项作业4为分项作业3的后续作业,节点占用时间亦相应推迟。经过第一次疏解后,分项作业4占用节点D37的开始时间为10:37:30,与发车分项作业24占用节点37的结束时间10:37:06间隔不足1 min,故两作业存在冲突,调车不能占用区段D23~D37,因而在分项作业3的进路区段D25~D23等待。第二次疏解导致在分项作业3再次产生等待延误时间1.8 min,经第二次疏解后方案2中再无进路冲突情况。 同理,方案1中,调车作业1的分项作业与其他作业在节点D23、D37多次存在冲突情况,导致调车只能在分项作业1的进路区段D31~D25等待,产生的等待延误时间累计长达48 min。 表4 进路安排方案比选 表5 方案2中分项作业3、4占用部分节点时间 图4 算法收敛过程 本文根据企业枢纽车站作业特点,基于调车作业时间连续性的考虑,建立了进路选择优化模型,并对企业车站进路安排进行优化。当调车作业与行车作业交叉冲突时,可保证行车作业优先,并完成对调车作业的时间疏解。当两项调车作业交叉冲突时,对冲突进行疏解,同时最大程度地保持调车作业的连续性不被干扰。对列车作业进路的选择排列上,该模型也可拓展到当到发晚点、作业延误等干扰因素发生时,对当前的进路分配方案进行动态调整,是本文后续的研究方向。通过对一实际大型企业铁路枢纽站的案例分析结果表明,在调车作业进路排列时考虑时间连续性,可避免大量进路冲突延误时间,使作业组织更加有序,且优化方案较未考虑时间连续性的情形下,提高效率21.6%,优化结果令人满意,具有实际应用价值与理论研究参考意义。4 案例分析
4.1 基本情况
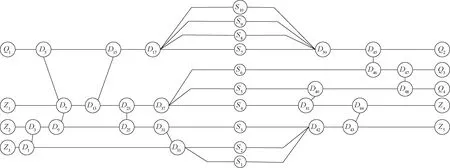
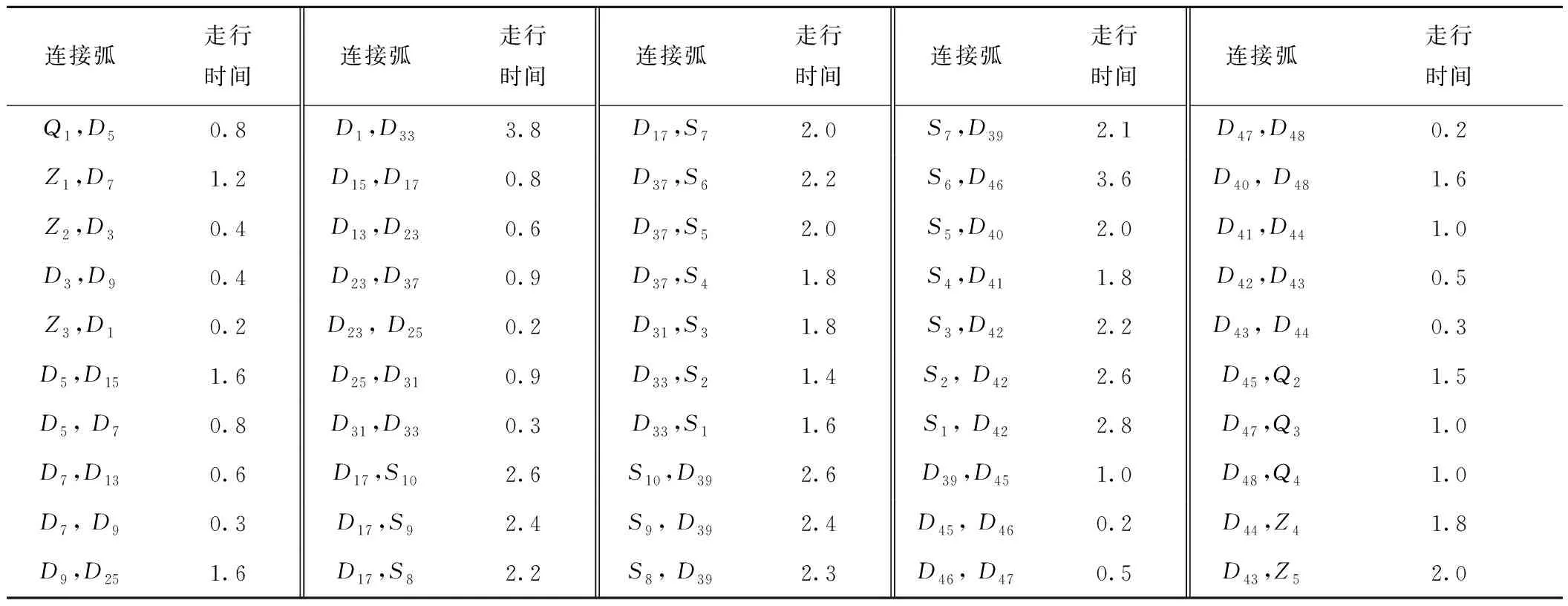
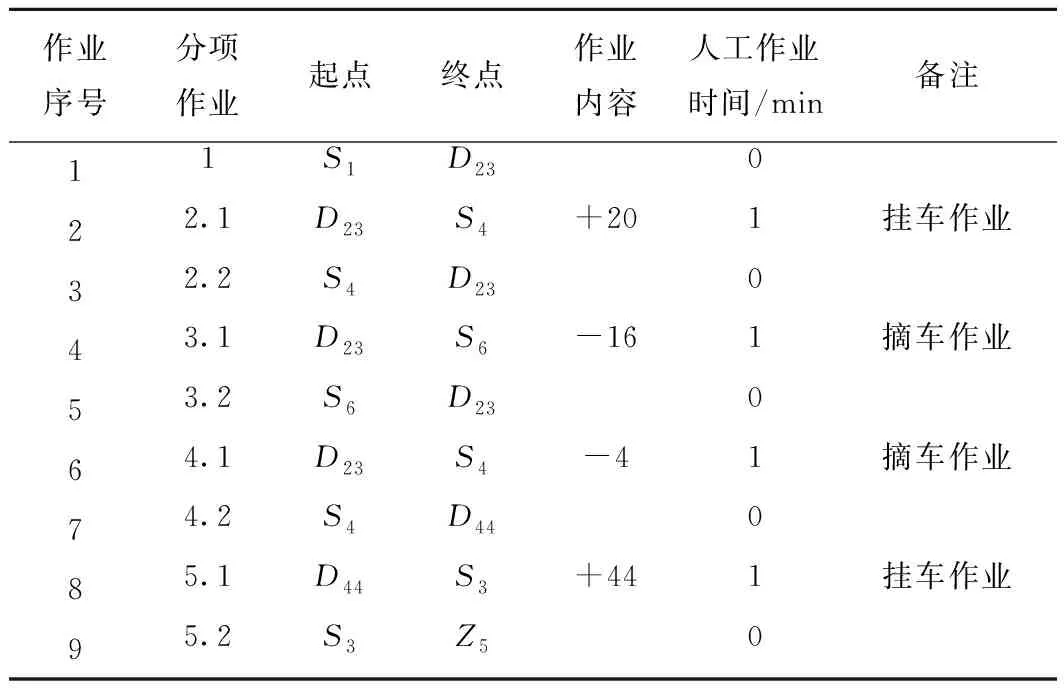
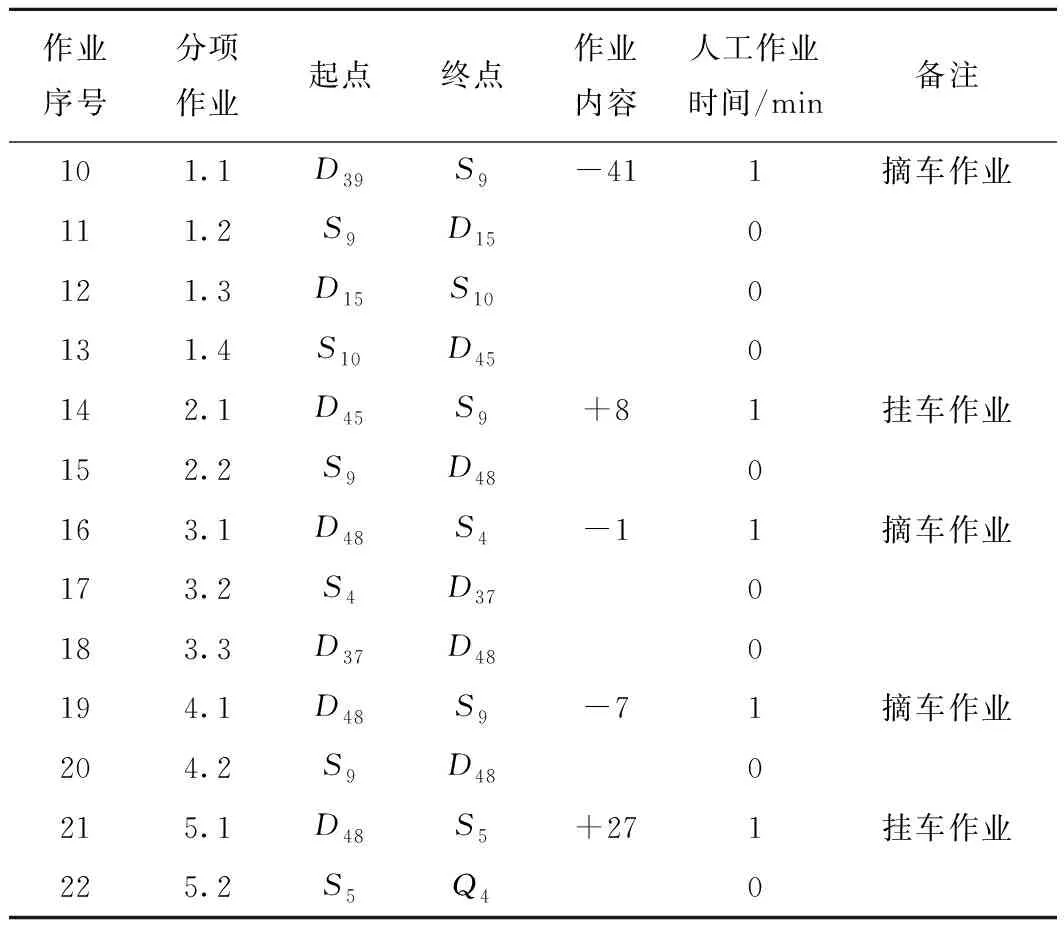
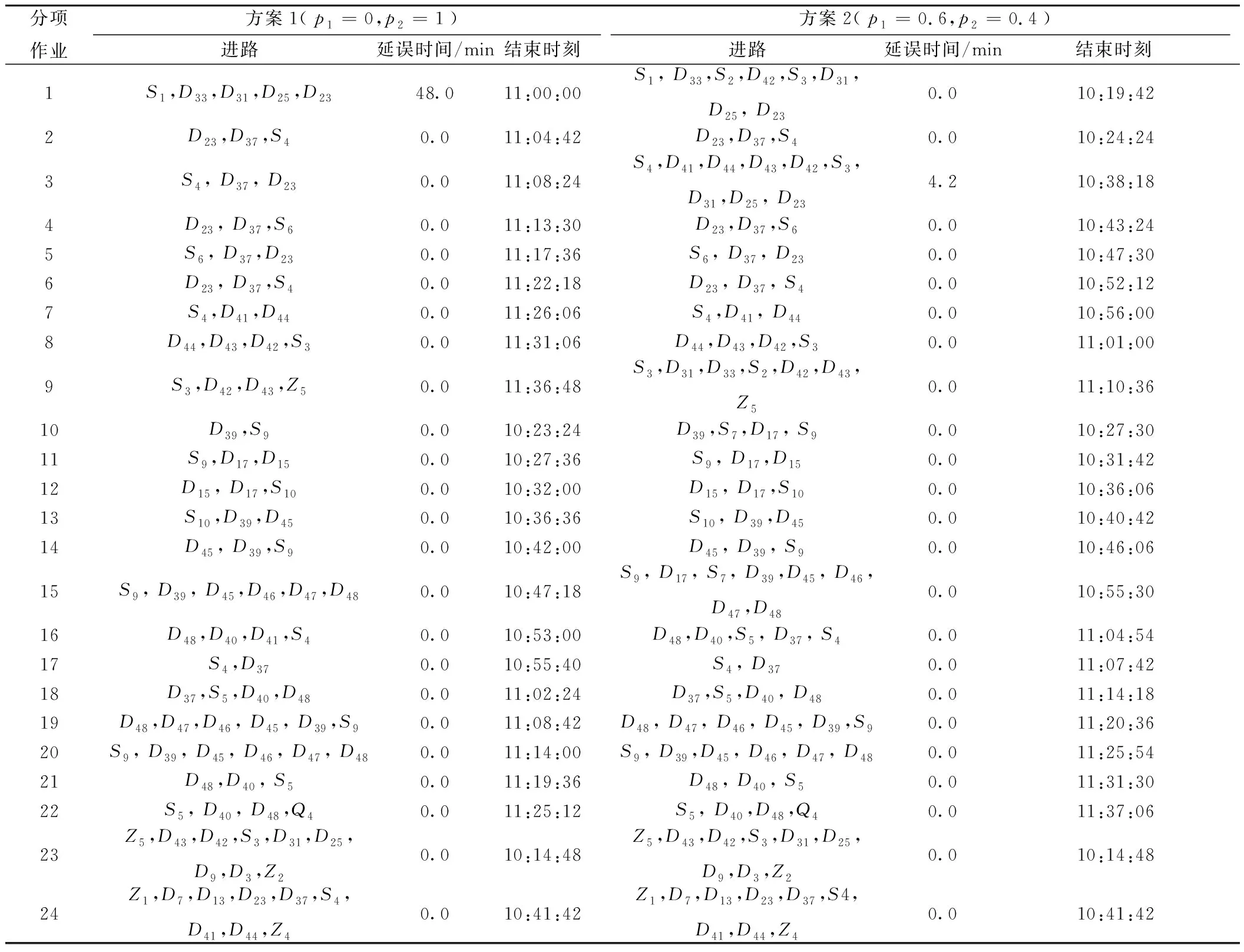
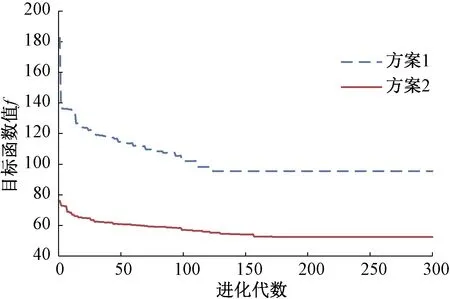
4.2 计算结果分析

5 结束语

