平衡二叉树的五步失衡调整方法探索

刘慧 张兆维

摘  要： 平衡二叉树的失衡调整不仅是数据结构课程的一个重要理论知识点，在软件开发过程中也有广泛的实际应用。旋转是对平衡二叉树进行失衡调整的主要手段，然而传统的左右旋转方法存在着操作繁琐、处理分散、不易被学生理解的问题。对此，文章提出一种五步失衡调整方法，该方法通过对四种旋转类型进行统一处理，简化了处理流程，从而降低了学生的理解难度。实际的教学结果验证了该方法的教学效果。

关键词： 数据结构; 平衡二叉树; 失衡调整; 平衡因子; 五步失衡调整

中图分类号：G642          文献标识码：A     文章编号：1006-8228（2020）11-78-04

Abstract： The imbalance adjustment of the balanced binary tree is not only an important theoretical knowledge point of data structure course， but also has a wide range of practical applications in the development of software. Rotation is the main means to adjust the imbalance of balanced binary tree. However， the traditional left-right rotation method has the problems of cumbersome operation， scattered processing and difficult to be understood by students. Therefore this paper proposes a five step imbalance adjustment method， which simplifies the process by unifying the processing of four types of rotation， so as to reduce the difficulty of students' understanding. The actual teaching results verify the teaching effect of this method.

Key words： data structure; balanced binary tree; imbalance adjustment; balance factor; five-step imbalance adjustment method

0 引言

作为“数据结构”课程[1]中的核心概念，二叉树在学生考研或工作中处于重要的地位，其中，平衡二叉树的失衡调整又是重重之重，引起了教学的广泛关注和研究。平衡二叉树是决定搜索性能的关键因素，一旦失衡，其搜索性能有可能会退化为线性表。失衡调整是将失去平衡的二叉树通过某种调整而成为一棵平衡二叉树，具有种类多样（“LL”、“RR”、“LR”和“RL”等四种）、操作繁琐（左旋转、右旋转、先左后右旋转和先右后左旋转等）、处理分散、容易混淆的特点，加大了学生的理解难度。

为了进一步降低失衡调整的理解难度，本文提出一种五步失衡调整方法，化繁为简，实用至上，以应对所有类型的平衡二叉树失衡情况。

1 面临的问题

平衡二叉树的失衡调整是“算法与数据结构”课程的核心内容之一，在考研和工作中都扮演着十分重要的角色。然而，在实际教学过程中，平衡二叉树的传统失衡调整方法不容易被学生理解和掌握，导致学生在学习该知识点时有畏难情绪，甚至存在厌学、逃学的情况。

针对平衡二叉树的失衡调整方法，众多专家和学者对此进行了广泛的研究和讨论[2-4]。在当前大部分教材中，根据平衡二叉树的失衡状态，失衡调整分为四类（“LL”、“RR”、“LR”和“RL”），在每一类中，失衡调整采用不同的左、右旋转操作来校正失衡[2]。朱宇[3]等对传统的旋转调整方法進行了改进，提高了调整速度和效率。陈海涛[4]等根据二叉排序树的原理，总结出四类简单的失衡调整方法。张标汉[5]利用“左小、中根、右大”规律提出一种填空法来调整平衡二叉树的失衡状态。朱洪浩[6]提根据二叉排序树的特点，提出一种基于平衡因子和二叉排序树的失衡调整方法，在一定程度上降低了学生理解和掌握的难度。

然而，上述方法虽有改进，但其核心思想还是围绕左右旋转调整方法展开的。表1对传统的左右旋转调整方法的具体处理方式进行了汇总。从表1中我们可以看出，传统的左右旋转方法有种类多样、操作繁琐、处理分散，容易混淆等特点，因而不易被学生理解。

2 五步失衡调整方法

为降低学生对平衡二叉树失衡调整的理解难度，本文提出一种五步失衡调整方法，不再对“LL”、“RR”、“LR”和“RL”四种失衡状态进行单独处理，而是采用一套统一的处理流程，简化了处理步骤，有利于学生对平衡二叉树的掌握。

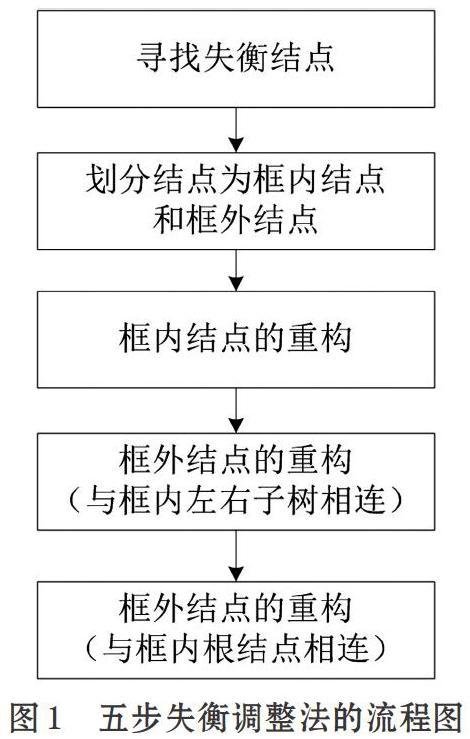
平衡二叉树的五步失衡调整方法的核心思想是依据失衡路线将结点分为框内结点和框外结点，通过这些结点的重构完成所有状况下平衡二叉树的失衡调整，该方法主要包含五个步骤，如图1所示，每一步的具体实现如下：

⑴ 寻找失衡结点：计算当前二叉树中各个结点的左右子树的高度差，即平衡因子，依据平衡因子确定最小失衡子树，将该子树的根结点定义为失衡结点;

⑵ 划分结点为框内结点和框外结点：从失衡结点开始，沿失衡方向，连续的三个结点构成一个三点框，这三个结点定义为框内结点，其余结点定义为框外结点;

⑶ 框内结点的重构：对三点框内的结点进行排序，其中中间值结点替代失衡结点成为根节点，小值结点成为左子树，大值结点成为右子树，构成“左小右大”的二叉排序树;

（4）与框内左右子树相连的框外结点的重构：与框内左右子树相连的框外结点，分别搬移到框内，分别构成原有结点的左子树或者右子树;

⑸ 与框内根结点相连的框外结点的重构：依据二叉排序树的定义，将其插入到二叉排序树的对应位置中。

为验证五步失衡调整方法对 “LL”、“RR”、“LR”和“RL”四种失衡状态的有效性，以下将采用该方法对各种失衡状态进行详细分析。由于“LL”型和“RR”型，“LR”型和“RL”型分别是对称的，本文仅考虑“LL”型和“LR”型，其余不再赘述。

⑴ “LL”型二叉排序树的五步失衡调整

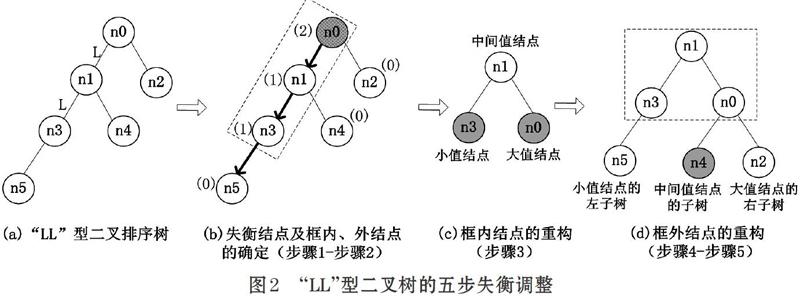
对于“LL”型二叉排序树而言，其失衡状态是由于在该树某一节点的左子树的左子树中插入新的结点造成的，如图2（a）所示，由于在n0结点的左子树的左子树中插入n5结点，造成当前二叉排序树的“LL”型失衡。

采用五步失衡调整方法对“LL”型二叉排序树进行失衡调整的具体处理流程如下：首先，寻找失衡结点，并依此确定哪些结点为框内结点，哪些结点为框外结点，如图2（b）所示，当前二叉排序树的失衡结点为n0，框内结点为n0、n1、n3，框外结点为n2、n4、n5;其次，重构框内结点，框内结点的排序结果为[n3?n1?n0]，以此排序结果构建新的二叉排序树，如图2（c）所示，中间值结点n1为根节点，小值结点n3为左子树，大值结点n0为右子树;最后，重构框外结点，框外结点n5和n2按照原有相连顺序进行重构，框外结点n4与新的根结点n1相连，按照二叉排序树的定义，将其插入到新的二叉排序树中，如图2（d）所示。

⑵ “LR”型二叉排序树的五步失衡调整

对于“LR”型二叉排序树而言，其失衡状态是由于在该树某一节点的左子树的右子树中插入新的结点造成的，如图3（a）所示，由于在n0结点的左子树的右子树中插入n5结点，造成当前二叉排序树的“LR”型失衡。

采用五步失衡调整方法，对“LR”型二叉排序树进行失衡调整的具体处理流程：首先，寻找失衡结点，并依此确定哪些结点为框内结点，哪些结点为框外结点，如图3（b）所示，当前二叉排序树的失衡结点为n0，框内结点为n0、n1、n4，框外结点为n2、n3、n5;其次，重构框内结点，框内结点的排序结果为[n1?n4?n0]，以此排序结果构建新的二叉排序树，如图3（c）所示，中间值结点n4为根节点，小值结点n1为左子树，大值结点n0为右子树;最后，重构框外结点，框外结点n3和n2按照原有相连顺序进行重构，框外结点n5与新的根结点n1相连，按照二叉排序树的定义，将其插入到新的二叉排序树中，如图3（d）所示。

如前所述，鉴于四种失衡类型的对称性，“RR”和“RL”型二叉排序树的五步调整步骤本文中不再赘述，有兴趣的读者可自行验证。根据以上说明，我们可以看到，五步失衡调整方法对“LL”、“RR”、“LR”和“RL”四种失衡状态都是有效的，能够以一套统一的流程进行处理，简化了处理流程，具有统一处理、操作易记、不易混淆等特点，有效的降低了学生的理解难度。

3 教学效果

为分析本文所提方法的实际教学效果，笔者对学生的知识掌握水平和学习情况等进行了面谈和统计。被调查的对象为294名普通二本高校的大二学生，其中144名学生采用传统的左右旋转法进行教学，150名学生采用本文提出的五步调整法进行教学。

图4中两组学生的平衡二叉树方面的考试成绩（转换为百分制）统计，将分数分为五档，来评估学生对知识的掌握程度。与传统调整方法（左右旋转）相比，本文方法能够降低低分段人数并提高高分段人数。比如，在传统方法下，不及格（低于60分）的比例占到55%，这也说明平衡二叉树的失衡调整是一个学习难点，尤其是对基础较薄弱的二本高校的学生。学生在掌握本文方法后，不及格率下降到40%，且高分段（80分以上）比例上升了12%。

图5调查了学生掌握失衡调整所花费的时间，调查对象为成绩60分以上的学生。利用传统掌握失衡调整方法，51%以上的學生需要花费三个小时以上的时间才能够掌握该知识。在本文方法下，81%的学生掌握失衡调整集中在三小时以内，甚至有12%比例的学生能够在45分钟内掌握。

综上所述，本文的五步调整方法能够降低学生的理解难度，减少学生的掌握时间，在一定程度上提高了学生的学习成绩和学习效率。

4 结束语

为了降低平衡二叉树中失衡调整的理解难度，本文提出一种五步调整方法来提高学生的学习效果。五步调整方法不再将失衡调整划分为四类，而是归为一类进行统一处理，能够显著地缩短学生的掌握时间和提高学生的学习成绩，取得了一定的教学效果。在五步调整方法基础上，如何进一步简化处理流程仍然值得我们进一步探讨。

参考文献（References）：

[1] 李春葆.数据结构教程（第五版）[M].清华大学出版社，2017.

[2] 严蔚敏，吴伟民.数据结构（第二版）[M].清华大学出版社，2008.

[3] 朱宇，张红彬.平衡二叉树的选择调整算法[J].中国科学院研究生院学报，2006.4：98-104

[4] 张标汉.平衡二叉树调整教学探讨[J].计算机教育，2009.10：53-54

[5] 朱洪浩.数据结构中平衡二叉树的教学探讨与研究[J].赤峰学院学报（自然版），2012.5：19-21

[6] 陈海涛，李宗惠.平衡二叉树的失衡调整方法探讨[J].中国科教创新导刊，2010.34：146-146