改进的混沌遗传算法求解无人机航迹规划问题

郑涛

摘  要： 针对无人机航迹规划问题展开研究，采用混沌遗传算法对无人机低空追击目标的航迹进行规划。该方法将无人机在低空复杂环境中的动力学模型离散化，结合约束条件，将三维空间划分为多个二维空间并利用栅格法进行二维建模，在二维空间下采用改进的混沌遗传算法来路径寻优，最终完成在三维空间中避开障碍物的航迹搜索过程。以建模工具Creator/Vega为仿真平台，建立仿真环境。仿真结果表明，该算法能够有效地规划出一条满足要求的航迹，且通过把三维空间转化为二维建模，避免了在三维空间求解的复杂性，提高了算法的工程实用性。

关键词： 三维航迹规划; 无人机; 混沌遗传算法; 混沌扰动; 扰动因子

中图分类号：TP301.6          文献标识码：A     文章编号：1006-8228（2020）11-26-05

Abstract： The paper discusses route planning issues of unmanned aerial vehicle by chaotic genetic algorithms， emphases on planning its tracking trajectory of avoiding obstacles at a low altitude. The method discretizes the dynamic model of low-altitude aircraft in complex environments， and according to all the constraints， the 3D space is divided into several 2D spaces， and the grid method is used for 2D modeling， and the improved chaotic genetic algorithm is used to optimize the path in the 2D space， thus completes the route planning process to avoid obstacles in the 3D space. Creator and Vega are used as modeling and developing tools to build the simulation platform. The simulation results prove that the proposed method can plan an approximate optimal path successfully， and avid solving the complexity of route planning problem in the 3D space by transforming 3D to 2D， which improves the engineering practicability.

Key words： three-dimensional route planning; unmanned aerial vehicle; chaotic genetic algorithm; chaotic perturbation; perturbation factor

0 引言

无人机航迹规划就是指综合考虑无人机机动性能、突防概率、碰地概率和飞行时间等约束因素下，寻找一条从起始点到目标点的最优或可行的飞行轨迹[1]。

由于遗传算法的鲁棒性，近年来有诸多学者，利用进化与遗传算法进行路径规划研究，取得了一定的成果。魏亭等人提出了基于稀疏A*遗传算法的无人机三维航迹规划方法[2]，稀疏A*算法是一种启发式搜索算法，它结合约束条件大大缩小了搜素空间，大大缩小搜素时间，但在三维空间中构造代价函数和启发函数，由于函数求解过程需要在立体空间中计算，大大增加了算法的难度。刘群芳，李军华在稀疏A*算法的基础上结合进化原理，引入了文化算法，基于稀疏A*算法与文化算法的混合算法实现了动态目标的无人机航迹规划，为有效解决复杂的多维非线性工程优化问题提供了一条分析方法，有很大的参考价值。本文利用混沌遗传算法（Chaotic Genetic Algorithm， CGA）并进行扰动因子的改进，综合考虑无人机的机动性能、地形高程障碍威胁以及飞行任务等多种因素，运用改进的CGA进行航迹规划。

首先利用Creator/Vega进行三维空间建模，然后参考文献[3]和文献[4]的方式，将三维空间搜寻转为二维空间求解，最后利用改进的CGA在二维空间展开航迹搜寻。经由对搜寻空间降维，下降算法难度，以获得提升搜寻效率的目标。

1 三维航迹转化为二维空间及在二维空间建模

CGA是在二维空间中的一种路径优先搜索算法，而低空无人机的航迹是三维的，因此必须把三维转化为二维空间搜索。在转化过程中，如何使用CGA从初始点到达目标点进行航迹搜索，如何进行节点扩展，如何选择候选节点就成为首要解决的问题。而正确的建立搜索空间，正是解决这些问题的先决条件。

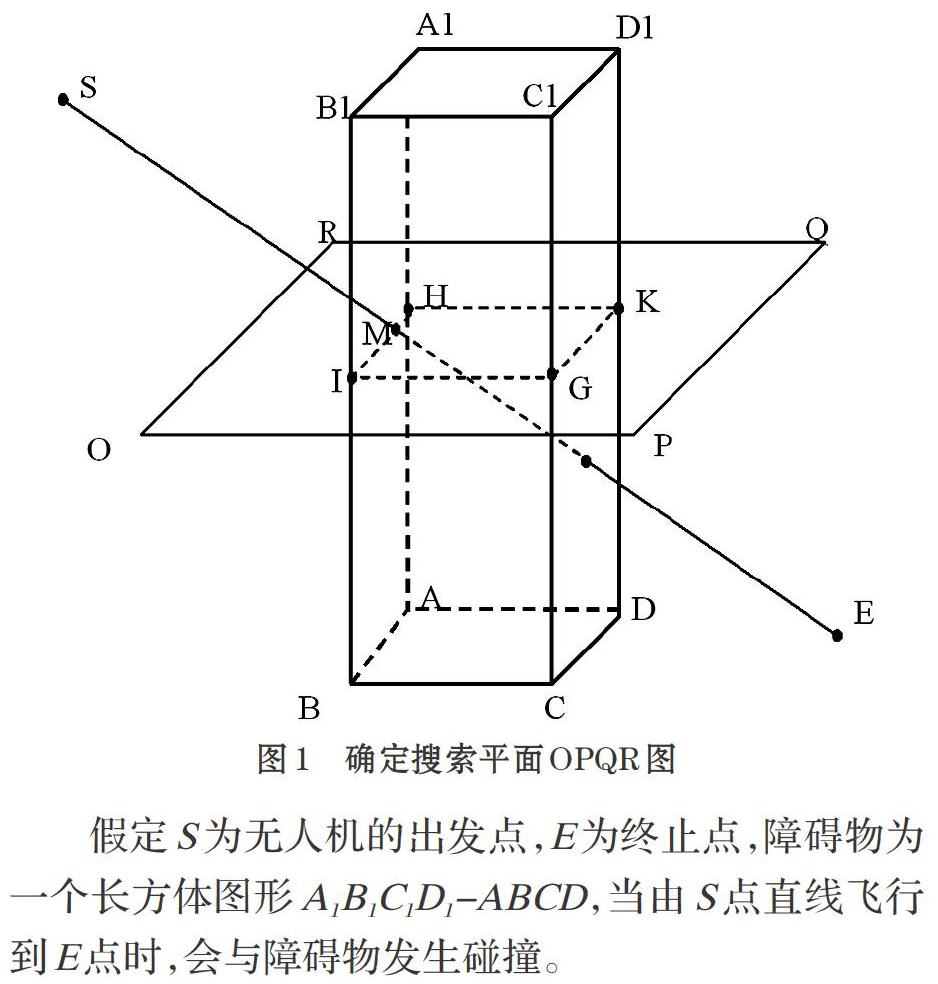
在三维空间中，目标和障碍物位置已知情况下，無人机自初始位置选择最佳避障路径向目标位置行进的过程（如图1）。

假定S为无人机的出发点，E为终止点，障碍物为一个长方体图形A1B1C1D1-ABCD，当由S点直线飞行到E点时，会与障碍物发生碰撞。

探索路径的三维搜寻空间，并绕开障碍物的前提下，过程建立如下：

Step1 连出发点到终止点的线段SE，找到SE线段与长方体障碍物的第一个交点M，经由M做与长方体顶面平行的平面，且此平面与该长方体依次交于H、I、G、K四点，改变扩展因子把此平面向周围扩大搜寻空间为OPQR。扩展因子的选取值以无人机能够旋转的最大角度α为基准。

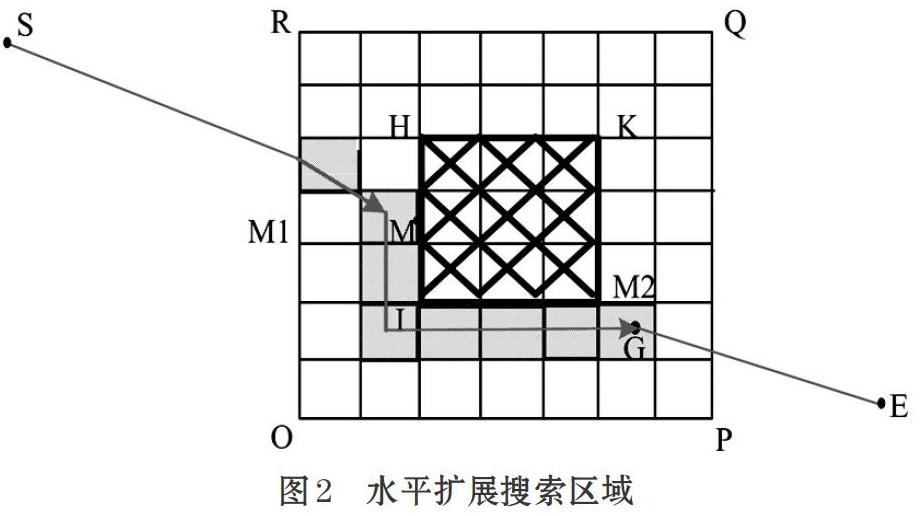
Step2 在二维水平空间确立搜寻区域（如图2）。

H、I、G、K四点组成的平面为障碍物在搜寻空间的投影平面，剩余的区域为可通过的区域。首先在搜寻平面上按栅格进行划分，按照栅格中心点的估计函数进行最优搜寻，找到向左或向右的飞行轨迹;然后将交点M向外扩展到点M1，在搜寻区域范围内寻找启发函数的最佳点M2;最后利用CGA可以找到由M1到M2的最佳搜寻路径。则二维搜寻路径最终由S到M1，再由M1到M2，M2到E。如图2所示。

Step3 在三维垂直空间确立搜寻区域（如图3）。

首先将OPQR平面以扩展因子的值不断向上扩展，当超出障碍物的顶部时，求得无人机向上飞行的轨迹搜寻区域;其次在该三维空间的顶面栅格中计算出离目的地E路径最短的栅格M2;然后应用CGA找出顶面中距离M1最短的栅格路径。则三维搜寻路径最终由S到M1，再由M1到M2，M2到E。

Step4 比较水平搜寻路径（如图2）和垂直向上搜寻路径（如图3）的路径值，最后确定最佳路径。

2 三维航迹规划及算法设计

2.1 无人机的约束条件与优化函数

无人机在飞行时有很多的约束限制，不同条件下约束各异。本文研究的无人机的主要约束条件包括：最小步长限制（[Smin]），最大转向角度（[θmax]），最大爬升/俯冲角，航迹距离约束，固定进入（接近）目标位置时的方向，飞行高度限制（[Hmax]）。综合以上约束条件，采用如下代价函数：

本文把从扩展节点到目标节点之间的直线距离作为启发函数[5]。即：

其中启发函数表示的其实是从当前节点到目标节点实际代价的下限，这样既满足可纳性，又满足一致性。

2.2 航迹规划的搜索步骤

Step1 粗略过滤障碍物。输入障碍物的坐标，判定此障碍物是不是在（Sx，Sy，Sz）到（Ex，Ey，Ez）所组成的长方体范围内。如果在，转到Step2;如果只有一部分在，则对区域边缘以n倍的Smin进行外扩，给n设定一个上限，这里设为3，转到Step2;如果不在，则对超出的范围的障碍物不予考虑，转到Step5。

Step2 在起始位置S到目标位置E的连线上，按照Step1设定的长方体范围判断，障碍物是否与SE直线相交。若相交，则计算线段SE与障碍物的交点，否则，转到Step5。

Step3 过交点上做与顶面平行和垂直的平面。对于平行平面，利用第3部分改进的CGA进行二维路径规划，找出最优路径轨迹（如图2）。对于垂直平面，使用扩展因子在平面中进行三维扩展（如图3），扩展后的平面同样采用CGA进行路径寻优，然后选择距离最短的那条路径段作为最终的轨迹。

Step4 将交点1、交点2…，所有轨迹线交点的坐标添加到Vega路径中，实现避障路径规划;

Step5 把S点移到当前位置，E点不变。按照SE方向继续向前搜索，若到达目标位置，则退出。若碰到障碍物，则转到Step2。

3 CGA二维路径规划及算法设计

在二维空间采用栅格法建模后，采用实数编码，运用CGA来优化路径。CGA是混沌算法（Chaos Algorithm，CA）和遗传算法（Genetic Algorithm，GA）的集成，是在求解复杂优化问题使用的最广泛的遗传算法的基础上，引入混沌扰动来解决单一遗传的早熟和局部收敛的算法。

CGA设计思想是首先按照遗传算法的基本步骤，即初始种群生成、选择、交叉和变异生成路径;然后引入混沌扰动。因篇幅所限，本文直接把遗传算法变异后的解集代入混沌优化式中，对遗传算法求解的详细计算过程不做描述。

3.1 随机扰动的确定

δ*为当前最优解（x1*，…，xr*）映射到[0，1]区间后形成的向量，称为最优混沌向量;δk为迭代k次后的混沌向量，δ′k为加了随机扰动后（x1，…，xr）对应的混沌向量[6]。其中0<α<1，采用自适应选取，这是因为搜索初期希望（x1，…，xr）变动较大，需要较大的α。随着搜索的进行，（x1，…，xr）逐渐接近最优点，故需要选用较小的α，以便在（x1*，…，xr*）所在的小范围内搜索[7]。本文应用式⑷确定α。

其中m为一整数，依优化目标函数而定;k为迭代次数。

3.2 CGA设计步骤

在3.1节确定扰动方案后，按CGA算法搜索待优化参数xi的步骤如下。

Step1 给变量设定取值范围[ai，bi]、群体大小m、混沌算子中的吸引子μi及父代间的互换率Pc1，Pc2和子代的变异率Pm[8]。

Step2 选用式⑸所示的Logistic映射，关系式如下：

其中i表示混沌变量的序号，i=1，…，r;u表示种群序号，u=0，1，…，m;βi表示混沌变量，0≤βi≤1;μi表示吸引子。

取u=0，μi=4[9]。先给式⑸赋r个微小差异的初值，得到r个混沌变量βi（1），（i=1，…，r）。依次取u=1，2，…，m，可得到m个初始解群[10]。

Step3 用载波法[11]，将选定r个混沌变量βi（u+1）分别引入到式⑹的r个优化变量中，使其变换为混沌变量[x'i]，混沌变量的取值范围，会相应切换到相应的优化变量的取值范围[12]。

Step4 把式⑵作為适应度函数的判断准则，计算式⑻生成的适应度值，把适应度值按照降序排列，因为f（X′）小于0时不能作为适应度，而且即便f（X′）非负，但若f（X′）对某一代群体相对变化范围过小，相当于两代值过于靠近或类同，会造成算法收敛速率很慢，因此还需要对f（X′）按下式作微小变化：

其中f′k（X′）为微小变化后的适应度值，fk（X′）为微小变化前的适应度值，f（X′）min为微小变化前的最小适应度值，f（X′）max为微小变化前的最大适应度值，m为群体大小，按式⑼调整后，适应度值均大于0，且适应度值的相对变化范围加大，便于加大收敛速度。

Step5 把所有变量按十进制进行编码，上一代群体中适应度值排在前10%的变量不参与遗传的三种操作（复制、交叉、变异），直接进入下一代群体，剩下的90%由这三种操作生成，对子代群体按规则解码。

Step6 对下一代群体按规则计算出符合自身条件的适应度值，然后按式⑾的规则适度调整，调整完毕按调整后的适应度值大小，对群體排序，求出适应度均值，并将其均值与适应度最大值按照式⑽进行比对，若式⑽成立，则认为寻优过程结束，输出结果作为最优值;若式⑽不成立，执行Step7。

Step7 在当前代群体中，选取适应度较小的90%个体，找到其对应的最优解，先按照式⑸的方法给其加一混沌扰动，将其转换为混沌变量，然后再按式⑹的方法映射为混沌优化变量，最后将混沌变量和混沌优化变量代入式⑶，进行迭代计算。随着迭代次数的增加，式⑷计算出的[α]值不断变化，迭代逐步向最优解逼近，逼近到先后两次计算出的适应度平均值之差小于预先给定的某个小正数[ε2]时，运算结束。

Step8 按适应度值大小再次对群体排序，求出适应度平均值，按式⑽的规则将其与最大值比对，若式⑽建立，则寻优结束并输出最优值，不然转到Step5。

按上述八个步骤对变异后的基因加入混沌扰动，且仅对某一代群体中适应度较小的90%的基因加混沌扰动，相当于对这些基因进行启发式的变异操作，可减少算法的进化代数，及早找到最优解;而且这种扰动有可能产生比前述10%较高适应度对应的基因更好的基因，有效地避免单纯的遗传算法局部收敛与早熟的问题，此外，由于遗传已生成10%的适应度较高的基因，只对剩下90%的基因进行混沌扰动，缩小了遗传算法的搜寻空间，可加速寻优速率。

4 仿真及结果分析

4.1 仿真环境

⑴ 软件环境

Vega是MultiGen-Paradigm公司最主要的工业软件环境，用于实时视觉模拟、虚拟现实和普通视觉应用。

Creator是MultiGen-Paradigm公司开发的一种用于创建逼真的三维模型和复杂地形的工具软件。

VC++2015是Microsoft公司推出的Microsoft Visual Studio 2015工具包里的软件之一，用于编写日常应用软件。

Matlab R2017b是MathWorks公司推出的专门用于科学、工程计算和系统仿真的高级语言。

⑵ 硬件环境

主机配置：Intel（R） Core（TM） i3-4130 CPU，1G内存，800G硬盘。操作系统：Windows 10。

4.2 仿真分析

本文首先在二维环境下仿真，在VC++平台下实现CGA路径寻优，并对相关数据借助Matlab曲线模拟进行分析;然后以Vega为仿真平台，利用Creator工具建立100km×100km的三维地理环境模型，包括沙漠、沼泽地、湖泊、城镇、乡村、道路、高大植物等，以城镇建筑物和高大植物为障碍物，演示低空无人机在击中目标时，避开这些障碍物寻优航迹的情况。

⑴ 二维环境仿真

在二维平面仿真中，运用栅格法对环境进行划分（如图4）。

从图4中可以看出，满足约束条件的前提下，寻到了一条接近最优解的路径。由于遗传算法的随机性，进行多次实验求其均值。

从图5看出，收敛速度较快，在第10代左右已寻到最优解，且随着进化代数的增加，完好保持了最优解，并未发生传统遗传算法的解丢失情况。

⑵ 三维环境仿真

仅考虑二维环境的路径规划是远远不够的，必须考虑在三维中的应用情况，验证是否实现二维到三维的平滑过渡与无缝连接。

为此，本文以Creator/Vega为仿真平台，建立仿真环境，完成对复杂地形地貌场景的设计。根据算法的设计情况，分别对水平与垂直两种情况下的航迹进行验证，避障仿真效果如图6和图7。

从图6、图7看出，用本文所设计方法进行三维环境路径规划，画面运行流畅，不仅能避开障碍物，而且基本符合真实性和实时性的要求，所规划出的路径也相对较优。

⑶ 运行时间与CPU占用率

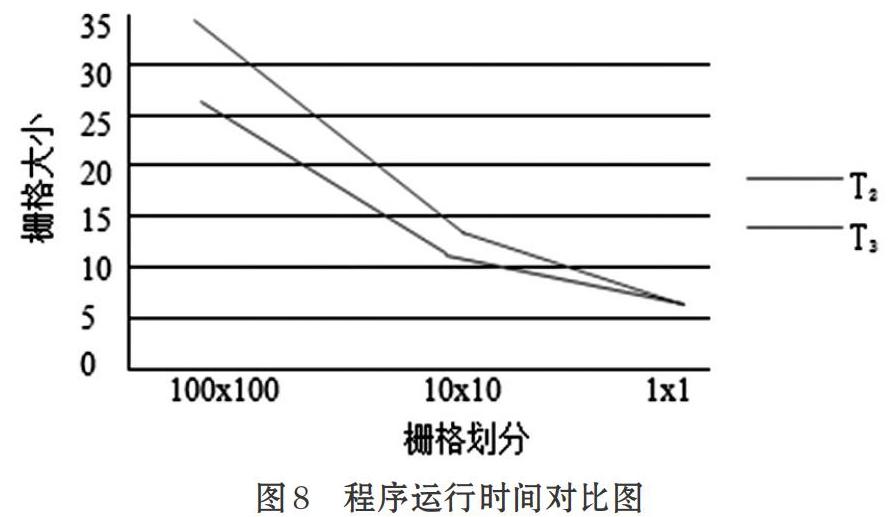
当栅格数较小时，改进的混沌遗传算法较A*算法有所改善但并不明显，是因为三维空间的数据值比较小，使得运算与二维的复杂度接近，如图8所示。

但是随着栅格数的增加，搜素空间也逐步加大，二维运算的优势逐步显现，运行时间大大缩短。因此当栅格数较小时，把三维空间转化为二维空间的效果并不理想，甚至有可能因为在转化过程中，转化程序也占用一定的时间而降低算法性能。

5 结束语

仿真结果表明，本文算法充分考虑了地形信息，计算出来的航迹能主动的对障碍物进行判断并绕行避障，在航迹最佳性，搜寻实时性和算法时效性上更高效，能够满足实时规划需要。

参考文献（References）：

[1] 李猛，王道波，盛守照.采用多重启发蚁群优化算法的无人机航迹规划[J].华南理工大学学报（自然科学版），2011.39（10）：37-43

[2] 魏亭，厉虹.基于稀疏A*遗传算法的无人机三维航迹规划[J].北京信息科技大学学报（自然科学版），2015.1：35-40

[3] ZENG Jia-you， XIE Yu-peng， BIAN Hong-fei， et al.Research on anti-saturation attack model of SAM to ARM[C]//International Conference on Communications in Computer and Information Science.Shanghai：Springer，2012：221-227

[4] Cheng L J， Ding Y S， Hao K R. An ensemble kernel classifier with immune clonal selection algorithm for automatic diseriminant of primary open-angle glaucoma[J]. Neurocomputing，2012.83（15）：1-11

[5] 马云鹏，牛培峰，陈科，闫姗姗等.基于混沌分组教与学优化算法锅炉NO_x模型优化研究[J].计量学报，2018.39（1）：125-129

[6] 李隘优.基于KCPSO算法对闽西地区崩塌地判释[J].江南大学学报（自然科学版），2015.14（6）：746-750

[7] 虞亚平.京津冀能源需求预测分析及发展对策研究[D].天津理工大学硕士学位论文，2017

[8] 张志军.长距离供水管道水锤分析优化与应用研究[D].西安建筑科技大学硕士学位论文，2016.

[9] 柳缔西子，范勤勤，胡志华.基于混沌搜索和权重学习的教与学优化算法及其应用[J].智能系统学报，2018.13（5）：818-828

[10] 李晓萌，王道波，郭继凯，杨华，王博航.基于某种生物启发式算法的无人机航迹规划[J].机械与电子，2018.36（11）：15-19

[11] 孙健，井立，刘朝君.突发威胁下的无人机航迹规划算法[J].飞行力学，2018.36（3）：52-55

[12] 余岩，王宏远，谢雨翔.一种在未知噪声下的快速波达方向估计方法[J].系统工程与电子技术，2010.32（4）：707-711