顺学而教的三次进化

张卫星

导 读：

顺学而教，即顺着学生的学习发展情况，采取与之相适应的教学方法。在教学“烙饼问题”时，笔者经历了三次改进。第一次改进求“稳”，让模型稳妥构建;第二次改进求“全”，让模型构建充实;第三次改进求“通”，讓模型构建融合。第三次改进的创新体现在学习视角、价值取向、学习资源、学生立场、共享意识五个方面。三次改进，三次进化，是对教学现代化的一种生动诠释和创新应用。

教育家陶行知说：“教的法子要根据学的法子。”随着新课程改革的稳步推进，顺学而教成为当下的教学主流。顺学而教，即顺着学生的学习发展情况，采取与之相适应的教学方法。那么顺学而教的内涵是什么？前提条件是什么？和教学现代化有什么关系？笔者结合自己近年来的教学实践，以“烙饼问题”教学的三次改进为例，呈现顺学而教的进化过程，阐述自己对顺学而教的理解。

一、定向模拟，稳建模型——第一次改进求“稳”

（一）呈现过程

2014年下半年，学校举行“有效建模”数学主题教研活动，由一位青年教师借用笔者班级执教“烙饼问题”一课。由于教师没有厘清教学思路，再加上学生模拟烙饼时间过长，时间到了还没有完成“烙饼问题”的模型建构，导致当天的配套作业没有完成。作为科任教师，笔者只能重新教学这节课。

为了不重蹈覆辙，笔者对教材进行了深入研究，决定把教学重心放在“烙3张饼”上，学生只定向模拟烙3张饼的方法，1张、2张饼的烙法由笔者演示完成，剩下的时间让学生推理烙4～10张饼的方法和所需时间。

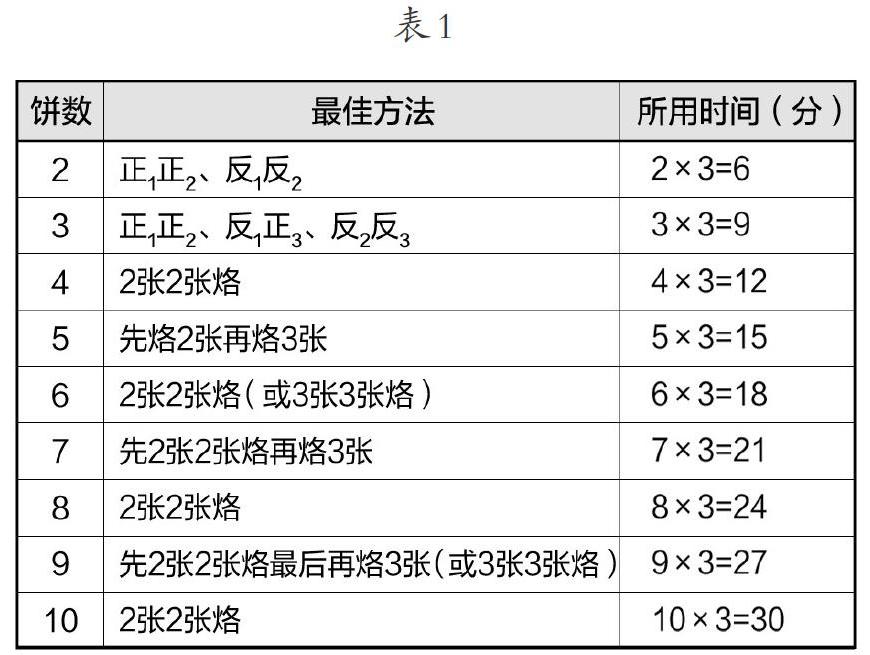
师：请同学们观察这张表1，能发现什么规律？

生：锅内每次烙2张饼最省时间。

生：双数张饼都是2张2张同时烙，很方便！单数张饼要2张、3张交替烙，有点麻烦！

生：饼增加1张，所用时间就增加3分钟。

生：所用时间=饼的张数×3分钟。

生：所用时间=饼的张数×烙1个面的时间。

学生的智慧是无穷的，预设的规律全部被发现。于是，笔者顺势提炼出“烙饼最少时间=饼的张数×烙1个面的时间”的规律。

（二）反思效果

建构“烙饼问题”模型后，从作业情况来看，效果比预设要好。但随着教学的深入，笔者发现，第一次改进建构的模型有缺陷——每次烙3张或3张以上饼时就不适用了。究其原因，是求“稳”心切所致。第一次改进基于“烙饼张数”这一视角，侧重于定向模拟，导致模型建构不够完善。为弥补这一缺陷，笔者只能在新课之后再补充一节拓展课。但到2017学年的时候，笔者发现这样处理多了一个课时，性价比不高，再加上第一次改进更多的是着眼于教，顺学味道不浓，于是“烙饼问题”教学就有了第二次改进。

二、一压一拓，充实模型——第二次改进求“全”

（一）呈现过程

为了在一节课内完成“烙饼问题”教学，笔者绞尽脑汁，最后决定适度压缩前面教学时间，有意识地安排如下这道拓展练习：妈妈要烙6张饼，每张饼两面都要烙，烙1个面要3分钟，如果每次锅内能同时烙3张饼，那么烙完这些饼最少需要多少分钟？

师：这道练习和刚才的练习有什么不同？

生：刚才每次烙2张饼，而这里每次烙3张饼。

师：烙法不一样了，还能用刚才提炼的模型来解决吗？

生：应该可以！3×3=9（分钟）。

生：烙法变了，应该不行吧！

师：到底行不行？我们可以用画示意图的方法验证一下。

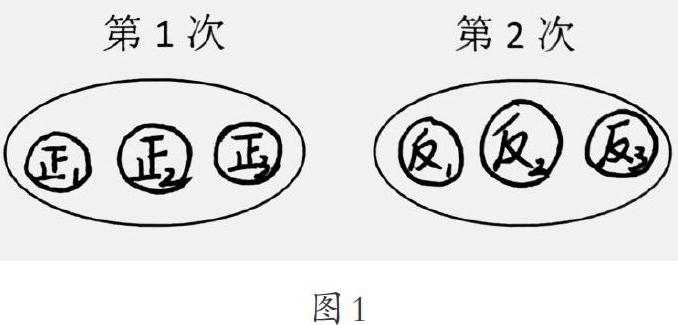
（学生开始在作业纸上画示意图，笔者把其中一个学生的作品呈现在投影上，如图1）

师：两次就烙完了，一共需要几分钟？

生：一次3分钟，两次3×2=6（分钟）。

生：烙法变了，计算方法也要变！

师：对！刚才我们提炼的“烙饼问题”模型有一个前提条件，那就是每次烙2张饼。如果每次烙3张或3张以上该怎么办？

生：用画示意图来解决。

师：画示意图有时候很麻烦，有没有更简便的方法？

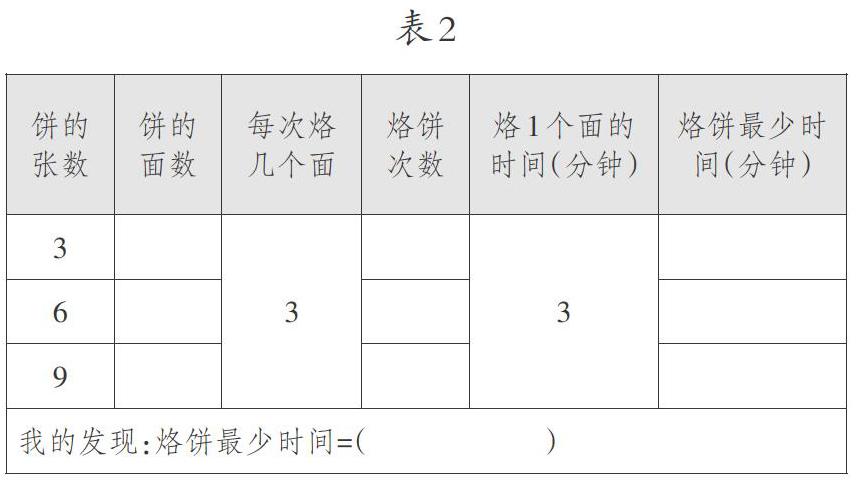
（学生一下子沉默了，面面相觑，不知所措。于是，笔者趁机出示表2）

以表2为载体，笔者和学生共同提炼出“烙饼最少时间=饼的张数×2÷每次烙几个面×烙1个面的时间”这一新模型。虽然这节课用了将近50分钟，但总算建模成功。课堂小结时，笔者明确告诉学生：“当每次烙2张饼时用‘烙饼最少时间=饼的张数×烙1个面的时间这一模型;当每次烙3张或3张以上饼时用‘烙饼最少时间=饼的张数×2÷每次烙几个面×烙1个面的时间这一模型。”

（二）反思效果

第二次改进，提炼出两个“烙饼问题”模型，能应对所有的“烙饼问题”，大多数学生能够做对配套作业，比前次教学效果更好，性价比更高。

但静下心来思考，发现第二次改进存在4个不足。一是资源意识不强，第二次改进使用PPT较多，板书内容较少，导致一些学生练习时找不到参考依据。二是模型缺乏联系，第二次改进构建的两个模型前提条件不同，再加上两个模型之间内在联系不强，导致一部分学生不知道该选哪一个模型，尤其是第二个模型过于冗长，一些学生难以透彻理解问题。三是过于求“全”，第二次改进时“饼的张数”和“烙饼次数”两个视角兼顾，侧重于充实模型，导致模型构建较复杂。四是顺学力度不够，第二次改进虽然关注学生的学，但关注教的成分居多。

鉴于上述4个不足，如果遇到学习基础不好的学生，估计很长时间也建不了模型。而2019学年笔者任教的班级的学生基础比较差，只能进行第三次改进。

三、转化视角，沟通模型——第三次改进求“通”

（一）呈现过程

事实上，“烙饼最少时间=饼的张数×2÷每次烙几个面×烙1个面的时间”这一模型最具普遍性，可以解决小学阶段的一切“烙饼问题”。只要我们将这个模型适度简化，从学生的认识角度加以分解，就能事半功倍。于是，笔者决定从“烙饼次数”这一视角入手，重新设计教学，构建学生更容易理解的新模型。

师：请同学们看黑板，有什么发现？

生：同时烙饼可以节省时间。

生：我发现“烙饼次数×烙1个面的时间=烙饼时间”。

師：对！烙饼最少时间=烙饼次数×烙1个面的时间。

师：1张饼有2个面，以3张饼为例，想一想烙饼次数怎么算。能列出算式吗？

生：1张饼有2个面，3张饼有6个面，一次烙2个面，需要烙3次。列成算式是：3×2÷2=3（次）。

师：为什么先乘以2，又除以2？

生：因为每张饼有2个面，所以要乘以2;因为每次烙2个面，所以要除以2。

师：嗯！现在大家知道怎么求烙饼次数了吗？

生：烙饼次数=饼的张数×2÷2。

生：不！烙饼次数=饼的张数×2÷每次烙几个面。

生：对！每个饼有2个面是固定的，而每次烙几个面要看题目要求，所以把“÷2”改成“÷每次烙几个面”更合适。

（至此，“烙饼问题”模型建构完整）

师：要求烙饼最少时间，要先求什么？再求什么？

生（齐）：要先求烙饼次数，再求烙饼时间。

（最后，笔者把板书补充完整）

（二）反思效果

课后的作业效果让笔者意想不到，原来基础较差的学生都会做了。在这一单元测试中，这一学期成绩是近几年最好的（试卷相同），第二次改进后平均分提高了近4分，第三次改进后平均分提高了近6分。而第三次改进的班级学生是近几年学习基础最差的，但取得的成绩却是最好的。可见教师的不断思考、不断探索、不断改进，才是构建省时高效课堂的关键所在。

毫无疑问，第三次改进是最成功的。只要我们稍加横向比较，就会发现它与前两次改进的相同点与不同点（见表3）。

从表3可以看出，第三次改进力度最大，其创新性体现在以下5个方面。一是学习视角，第三次改进是在充分研读学情和教学反思的基础上，捕捉到“烙饼次数”这一视角，构建的两个“烙饼问题”模型有前后依存关系，大部分学生能够理解。二是价值取向，第三次改进专注于“烙饼次数”，探索“烙饼次数”与“烙饼时间”之间的关系，侧重于构建两个融为一体的模型，求“通”。第一次改进求“稳”是为了保底，第二次改进求“全”是为了效率，第三次改进求“通”是为了素养。三者相比，求“通”价值最高。三是学习资源，第三次改进只是在烙3张饼的时候用PPT动态演示，其余重要信息都在黑板上有序呈现，适合学生随时参考和回顾。同时板书结构与“烙饼问题”模型结构一致，有利于学生快速建模。可见，第三次改进是把板书作为一种学习资源加以利用。四是学生立场，第三次改进着眼于让学生学得轻松，更多关注学生学的品质。五是共享意识，第三次改进笔者有意识地把“烙饼问题”的板书在朋友圈发布，有些教师直接采用这种教法。

（三）提炼主题

第三次改进的成功在于学生立场的充分确立。如果说学生立场是一种教学观念，那么顺学而教就是与之相应的教学行为。经历三次改进，顺学而教的内涵、前提以及它与教学现代化的关系也就明朗了。

1.内涵。从学生的实际出发，顺着学生的思路展开教学，着力破解教学中存在的实际问题。第一次改进从研读教材出发，控制模拟烙饼的时间，保证“烙饼问题”模型顺利建构。第二次改进设计拓展练习，借助画示意图和预设表格建构第二个模型，充实“烙饼问题”模型。第三次改进从“烙饼次数”入手，重新构建出两个简短、关联的模型，以新视角充实板书资源，让学生可以随时参考，把学习成果在朋友圈发布，让更多教师和学生受益。

2.前提。第一次改进实质上是对研读教材不到位、教学思路不清晰等教学行为的改进，第二次改进实质上是对教学缺陷的一种弥补，第三次改进实质上是对学习烦琐的一种改进。一句话，三次改进都是基于对本班学生现实学习问题与结果的反思。教师只有直面问题，不断反思，顺学而教才能更接地气。

3.关系。顺，即顺着学生的思路、立场、视角设计并展开教学，第三次改进中以“烙饼次数”为视角展开就是一种有价值的顺。教，即针对学生现实存在的问题创造性地运用一些学生认可的方法，第三次改进转换视角，把板书作为一种学习资源，让学习成果共享，就是一种有价值的教。顺学而教，即顺着学生的变化随时调整教学策略，是一种创新视角下的教学现代化，是对教学现代化的一种生动诠释和创新应用。

总之，顺学而教是不断发展的，犹如“烙饼问题”教学的不断改进。三次改进，三次进化，成就高品质的顺学而教。

（作者单位：浙江省仙居县田市镇中心小学）