预制预应力砼T梁侧弯线形分析研究*
王贵
(湖南建工交通建设有限公司, 湖南 长沙 410004)
装配式预应力砼梁桥以其标准化、规范化、现场施工便捷和经济效益良好等优势,被广泛应用于工程建设项目中。湖南地区已建和在建项目中有大量桥型选择装配式预应力砼梁桥,实地调研发现在实际施工中由于T形预制梁截面相对较小、刚度较弱、自身横向抗弯刚度较小,在张拉预应力钢束后,受多种因素的综合作用,T梁产生一定程度侧弯,预应力钢束的孔道定位偏差对侧弯变形量的影响更明显。过大的变形不仅影响后续施工的正常进行,同时严重影响结构的安全性和耐久性。当前,有关侧弯变形的研究多集中在定性分析和侧弯变形控制方面,对于定量计算的讨论还较少,相关规范性文件对T梁侧弯变形量的允许值也没有具体规定,仅部分地区在地方标准中进行了部分阐述。该文依托平益[平江(湘赣界)至益阳安化]高速公路矮洲汨水大桥,通过实地调研了解T梁侧弯变形情况,采用有限元数值计算模型模拟钢束孔道偏位,计算侧弯变形量,利用数学统计方法,得出符合数据变化规律的曲线形式,为T梁侧弯变形研究提供理论参考。
1 侧弯变形影响因素分析
影响预应力T梁侧弯变形的因素很多,包括预应力钢束在施工过程中的张拉顺序及张拉工艺、钢束孔道定位偏差、构件截面形式和尺寸大小、张拉时砼的强度等。
施工经验表明,存在多根预应力钢束时,不同钢束施工顺序产生的侧弯值不相同,在其他项目满足规范要求的前提下,通过优化钢束张拉顺序,可保证钢束侧弯变形满足规范要求。严格按设计施工要求和规范标准进行操作,可使这些因素对T梁侧弯变形的影响程度降到最低。矮洲汨水大桥T梁预制场调研结果表明,钢束孔道定位偏差是一个突出问题,波纹管在施工中产生定位偏差,将直接导致波纹管中的钢束偏离设计位置,张拉后将在非轴向上产生额外的应力,特别是对于腹板薄、高跨比小、横向刚度较小的T形梁,波纹管施工时的定位偏差将直接影响钢束合力的作用点,引起主梁侧弯变形。砼浇筑过程中,砼的振捣也容易引起内置波纹管产生较大内移或外偏,从而引起钢束偏位,导致主梁侧弯变形。因此,重点针对钢束孔道定位偏差引起的钢束侧弯变形进行分析。
2 数值模拟分析
从预应力孔道定位偏差着手,研究T梁侧弯变形量沿梁纵向变化的规律。根据矮洲汨水大桥40 m预应力T梁设计图纸,利用MIDAS FEA建立数值计算模型,划分单元进行侧弯变形量数值计算。
2.1 模型参数
该桥位于平江县安定镇官滩村、美潭村,桥位区最低地面高程约72.56 m(中部汨水两岸),最高约115.17 m(伍市端桥台),相对高差约40.0 m。桥位区有乡村机耕道正交下穿通过,交通较便利。全长727.8 m,全桥采用40 m简支变连续T梁结构,共分为6联,桥跨布置为18×40 m预应力T梁,桥面净宽2×11.75 m。主梁采用C50砼,设置N1、N2、N3、N4、N5 5组预应力钢束,边梁和中梁预应力钢束均不设平弯段。钢束采用1860高强钢绞线,截面面积1 400 mm2,边梁钢束截面面积1 540 mm2,中梁钢束布置形式见图1、图2。表1为该桥5组15束钢束孔道定位偏差情况。

图1 钢束竖弯示意图(单位:cm)
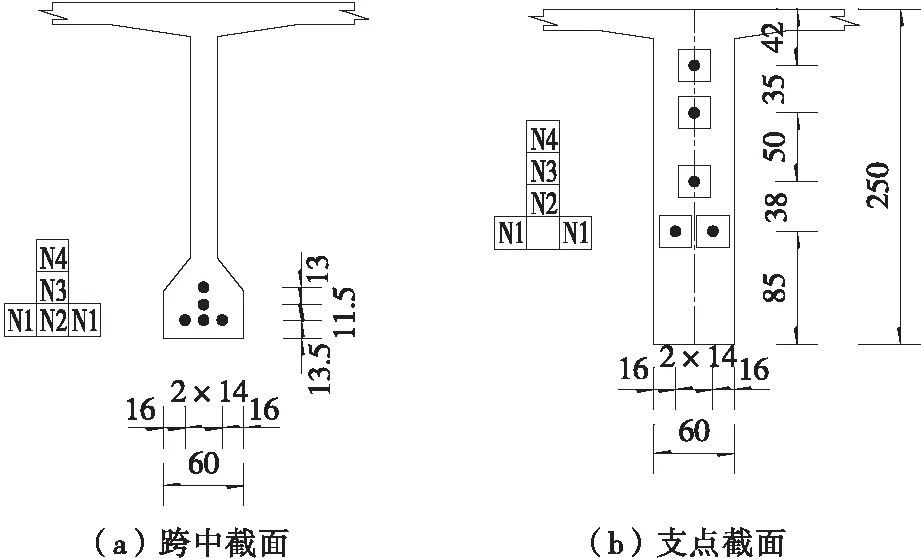
图2 支点孔道和跨中孔道定位示意图(单位:cm)
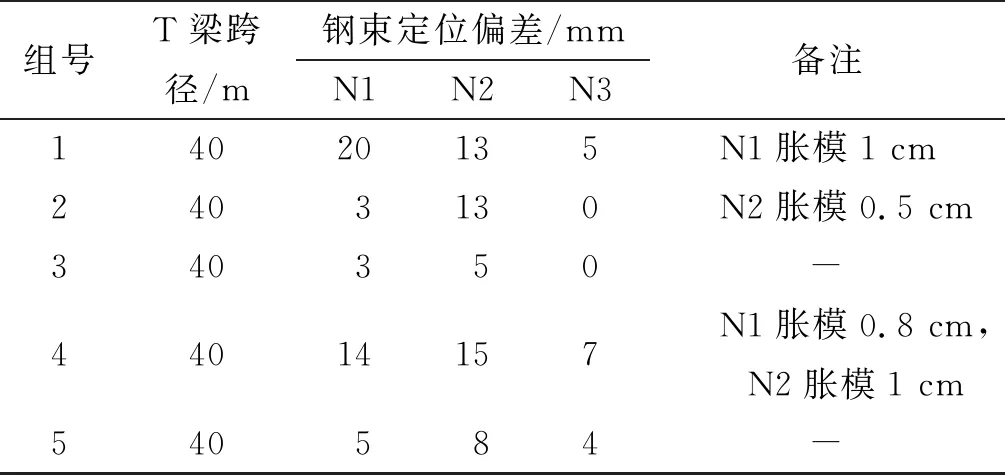
表1 T梁截面预应力钢束定位偏差数据
2.2 模型建立
利用有限元软件分别建立40 m T梁的边梁和中梁实体模型,输入预应力钢束单元,计算钢束整体同向偏位2、4、6、8、10、12、14 mm时的侧弯变形量。模型中,X轴与梁纵向中线重合,Y轴平行于梁横桥向、垂直于X轴。中梁模型T梁侧弯变形见图3。

图3 T梁侧弯变形示意图
2.3 数据提取
根据CJJ 2-2008《城市桥梁工程施工与质量验收规范》,预制梁侧向弯曲小于L/1 000(L为构件长度)且不大于10 mm。中梁和边梁钢束整体同向偏位10 mm时的侧弯变形量见表2、表3。
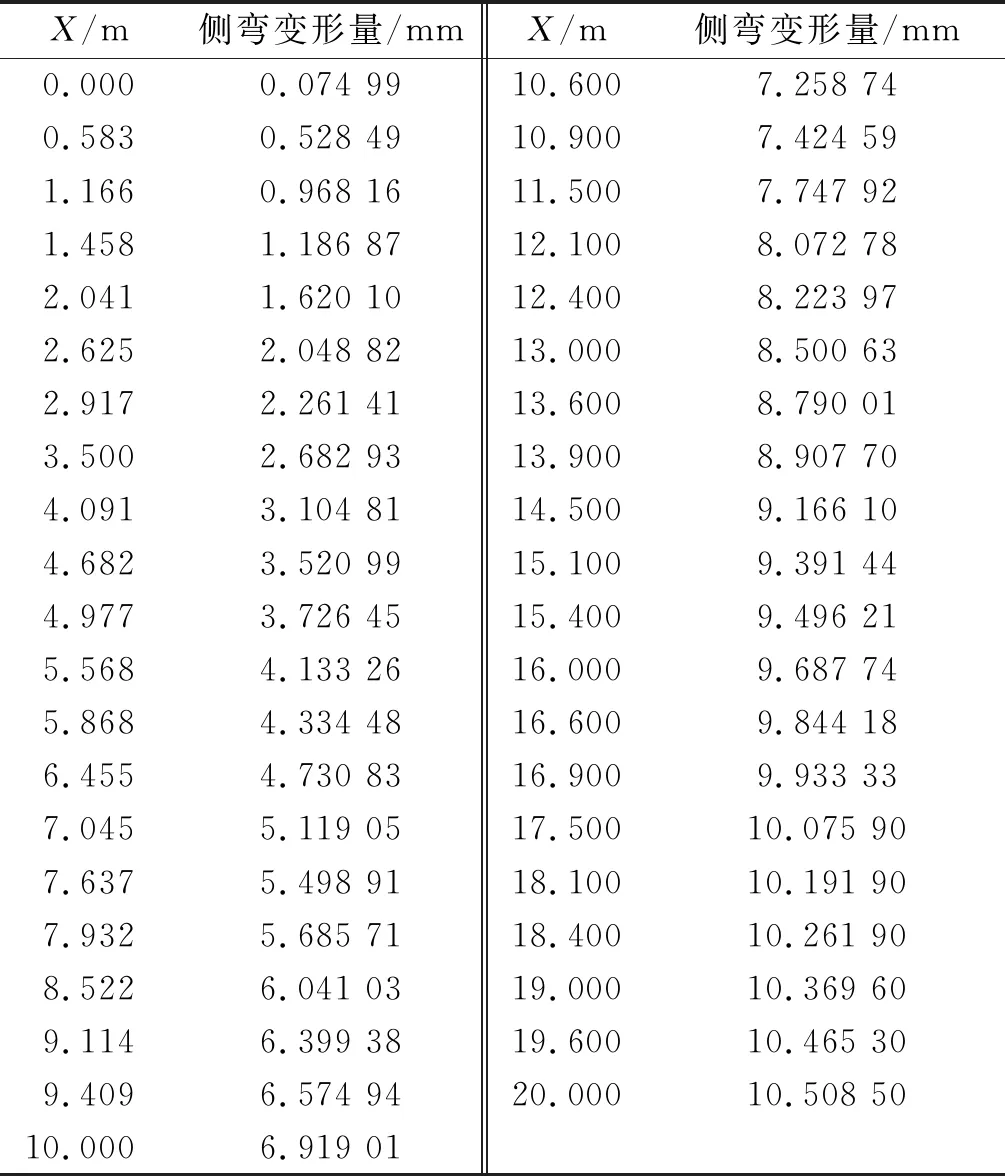
表2 中梁纵向中轴线各点侧弯变形量

表3 边梁纵向中轴线各点侧弯变形量
3 侧弯线形拟合分析
利用数学统计方法对表2、表3中数据进行分析处理和数学拟合,确定符合数据变化特征的曲线方程。分别选取二次多项式、三次多项式、四次多项式作为目标函数。
3.1 中梁
利用MATLAB软件对表2中数据进行数学拟合,所得曲线方程见表4。

表4 中梁侧弯变形曲线方程拟合结果
通过数学拟合所得曲线方程反算中梁侧弯变形量,结果见表5。各函数对中梁侧弯变形量的拟合结果对比见图4。
由图4可知:二次多项式计算值和三次多项式计算值吻合程度较高,二者变化规律和发展趋势基本相同,说明利用二次、三次多项式来描述中梁侧弯变形的发展规律的误差基本相同。在顶点和两侧部位,二次、三次多项式曲线与数值模拟计算值之间存在一定距离,吻合程度较低。四次多项式计算值和数值模拟计算值的吻合程度较高,利用四次多项式描述中梁侧弯变形的误差比二次、三次多项式的小,具有更高的计算精度。

表5 中梁纵向中轴线各点侧弯变形量计算结果
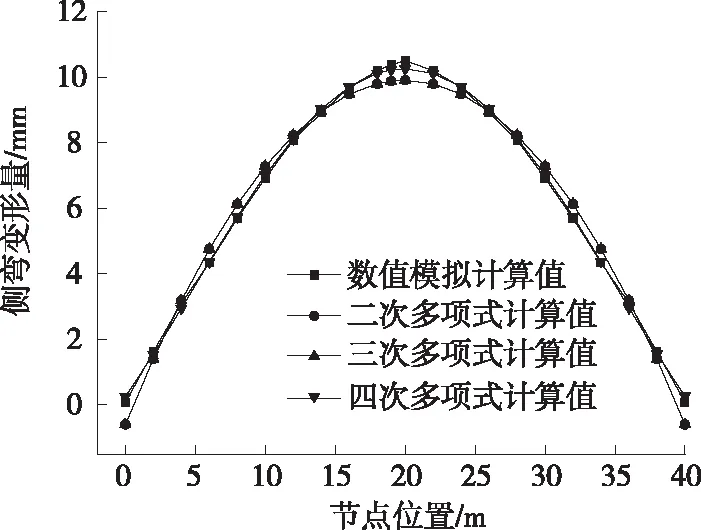
图4 中梁函数拟合结果对比
3.2 边梁
与中梁类似,对表3中数据进行数学拟合,所得曲线方程见表6。

表6 边梁侧弯变形曲线方程拟合结果
通过数学拟合所得曲线方程反算边梁侧弯变形量,结果见表5。各函数对边梁侧弯变形量的拟合结果对比见图5。
由图5可知:4条曲线的变化规律和发展趋势大致相同。二次多项式曲线在两侧部分均低于数值模拟计算值,三次多项式曲线在极值和曲线两侧部分与数值模拟计算值吻合程度较低,四次多项式曲线与数值模拟计算曲线的吻合程度最高。说明利用四次多项式描述边梁侧弯变形的误差比二次、三次多项式的小,具有更高的计算精度。

表7 边梁纵向中轴线各点侧弯变形量

图5 边梁函数拟合结果对比
4 结论
(1) 预应力钢束孔道定位偏差会对预应力定位产生不利影响,钢束孔道定位偏差将直接引起T梁侧弯变形。
(2) T梁发生侧弯变形后,无论是中梁还是边梁,其侧弯变形曲线方程更接近于四次多项式。

