五跨先简支后连续梁桥的延性抗震设计

易祥军

(海南省交通规划勘察设计研究院， 海南 海口 570206)

地震激起的惯性力较大，对于普通结构，若单纯依靠强度来抵抗地震，会造成巨大的材料浪费。目前，大都将“小震不坏，大震不倒”的二阶段设计方法作为基本设防思想，即中小震作用下结构处于弹性状态，以强度破坏为准则；强震作用下结构可发生一定塑性变形和有限损伤，以延性破坏为准则。弹塑性动力时程分析法是随着强震记录增多和计算机技术的广泛应用发展起来的，该方法从选定合适的地震波出发，通过有限元动力模型建立地震振动方程，通过逐步积分对方程进行求解，计算地震动过程中每一时刻结构的响应，从而分析地震作用下结构弹性和非弹性阶段的内力、位移变化。

1 地震波的选取和调整

地震动输入的不确定性是支配结构地震响应不确定性的重要因素。地震动的主要特性可通过幅值、频率和持续时间来描述。

根据特征周期与场地特征周期比较相近的原则选取3组地震波进行调整，以与E2地震作用下规范反应谱相适应为目标。调整前的地震波见表1。

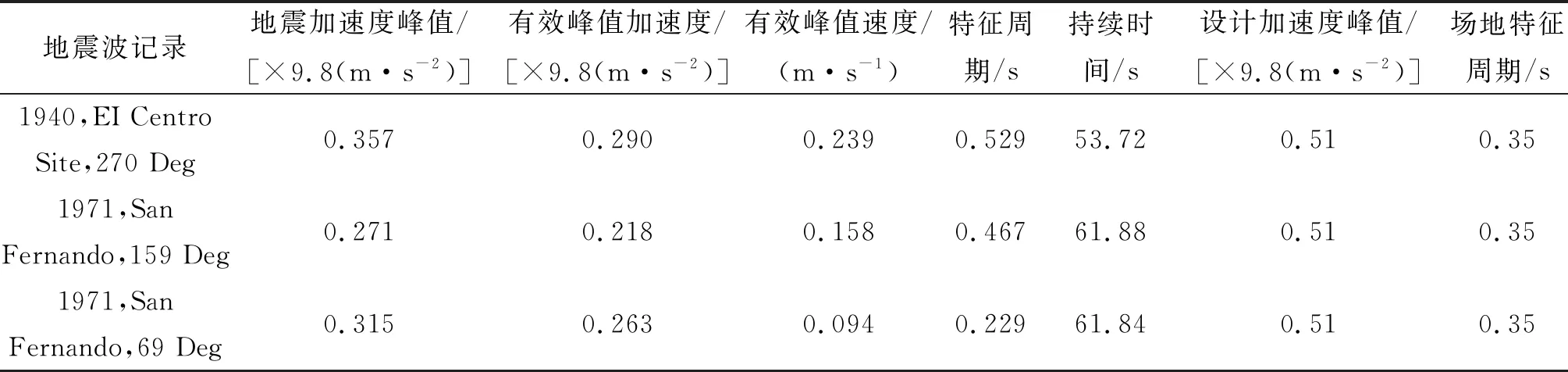
表1 调整前的地震波特性

调整后的地震波保证有效峰值加速度和特征周期与E2地震作用下规范反应谱相同。限于篇幅，不具体描述。地震波1调整前后加速度反应谱曲线见图1。

2 双折线滞回模型

弹塑性动力时程法分析中，实际地震荷载为反复荷载，通过定义滞回曲线的变形规律来反映。鲍雷T.等把结构或构件的滞回延性定义为在抗力始终没有明显下降的情况下，结构或构件所能承受的反复弹塑性变形循环的能力。此外，钢筋砼结构的特点是卸载后刚度低于初始刚度，称为刚度退化，且刚度变形与循环荷载的履历有关。根据刚度退化的特点采用Clough双折线计算模型，初期加载时效应点在2条不同斜率的骨架曲线上移动(见图2)，卸载刚度按式(1)计算。根据式(1)，卸载刚度随着屈服后变形的进展而逐渐减小。

图1 地震波1调整前后加速度反应谱曲线

(1)

式中：KR为卸载刚度；K0为弹性刚度；Dy为卸载开始时相应区域的屈服变形；Dm为卸载开始时相应区域的最大变形，对于还未发生屈服的区域取屈服时的变形；β为确定卸载刚度的经验系数，一般取-0.4。

图2 Clough模型的滞回曲线

3 结构性能分析

3.1 工程概况

南渡江大桥位于海南省澄迈县永发镇，跨越南渡江。上部结构采用7 m×(5×30) m先简支后连续预应力砼箱梁，梁高1.6 m；采用柱式桥墩，直径均为1.6 m；桩直径为1.8 m。桥型布置见图3。

采用MIDAS/Civil有限元软件对桥梁进行分析，采用梁格模型建模。取7联中墩高最矮的一联作为算例，墩高见表2。墩柱纵筋配筋率为0.98%(40φ25)、配箍率为0.63%(φ16@80)。等效塑性铰长度按JTG/T B02-01-2008《公路桥梁抗震设计细则》计算。计算模型见图4。

图3 南渡江大桥连续箱梁桥型布置(一联，单位：cm)

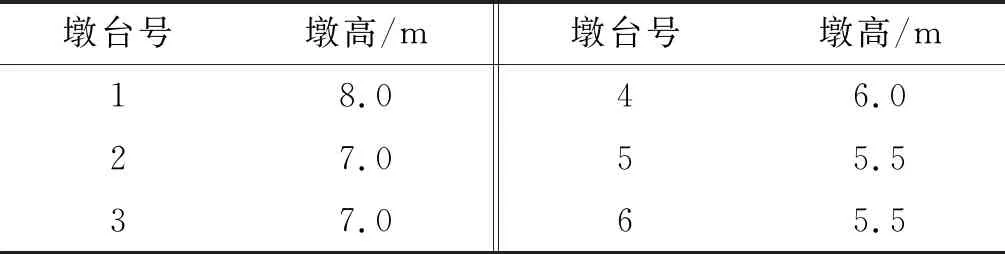
表2 计算模型桥墩高度

图4 南渡江大桥连续箱梁桥计算模型

3.2 结构内力响应分析

顺桥向和横桥向塑性铰的区别在于屈服特性不同：顺桥向塑性铰轴力恒定，屈服强度一定；横桥向塑性铰需考虑轴力变化，用屈服面描述屈服强度。二者并无本质区别，由于篇幅所限，仅沿顺桥向输入地震波进行分析，线性时程分析和弹塑性时程分析主要内力对比见表3。

由表3可知：地震波1、2、3作用下，考虑塑性铰延性后，墩底弯矩分别平均折减40.7%、35.6%、36.9%,墩顶剪力分别平均折减35.0%、19.6%、28.3%。当地震波特性不同时，塑性铰耗能对弯矩折减程度较稳定，对剪力折减程度差别较大。即使折减程度并不一定，但始终存在一个规律,即塑性铰可以调整结构内力分布，使各墩原本差别较大的内力变得均匀。如对于地震波1、2、3，线性时程分析得到的各墩底弯矩分别与平均值最大相差28.4%、69.4%、11.9%，而弹塑性时程分析得到的墩底弯矩分别与平均值最大相差7.5%、4.6%、4.9%，原因在于塑性铰屈服后位移显著增大的同时，荷载增加缓慢，使其余未屈服的桥墩分担了荷载。说明塑性铰的调节作用很显著，这一规律对于桥墩统一设计非常有利。

表3 线性时程和弹塑性时程分析内力对比

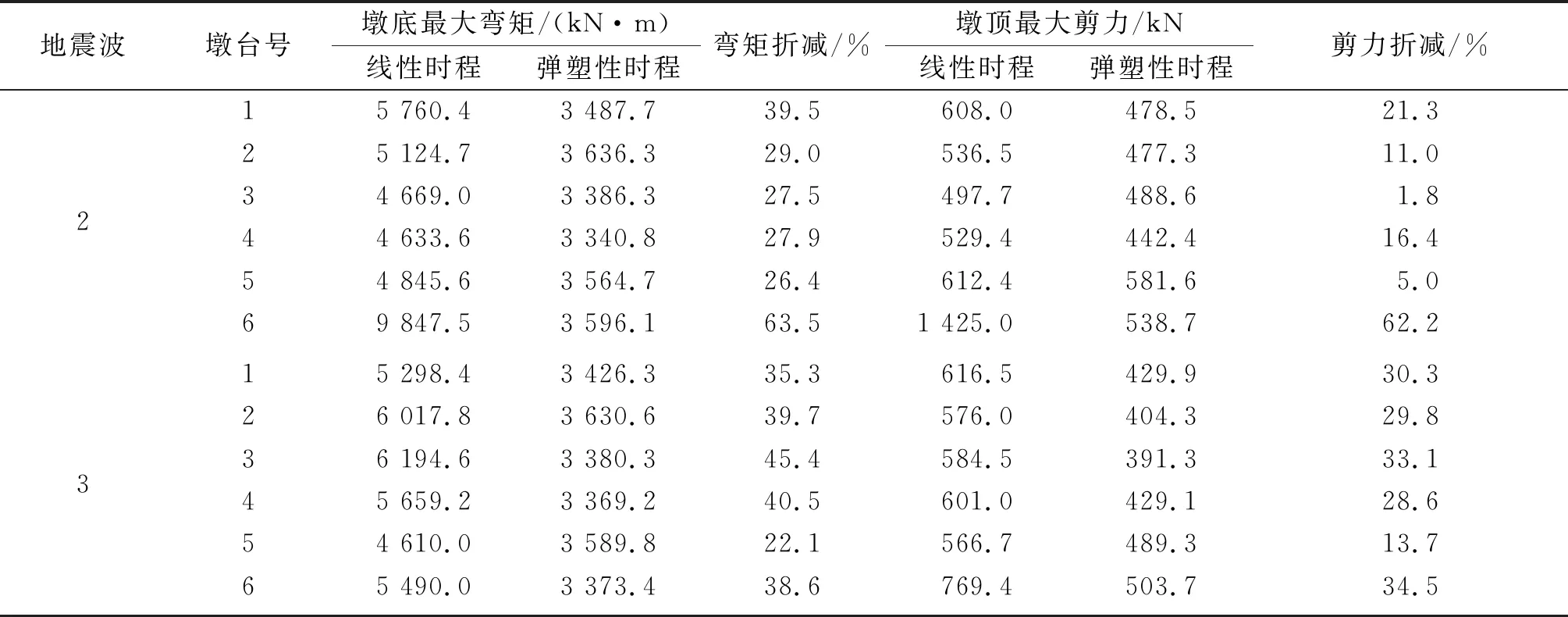
续表3

3.3 塑性铰滞回特性

图5～7为不同地震波作用下1#、6#墩墩底弯矩-转角滞回曲线。

由图5～7可知：墩底弯矩-转角滞回曲线外轮廓围成一定的面积，体现了塑性铰的耗能能力，面积越大，吸收能力越强。然而计算模型仍然不能反映结构是否发生塑性破坏，即塑性铰变形是否超过其延性能力，还需另行判断。该桥各墩墩底塑性铰延性能力与需求见表4。

由表4可知：各塑性铰延性能力有较大富余。

图5 地震波1作用下典型塑性铰滞回曲线

图6 地震波2作用下典型塑性铰滞回曲线

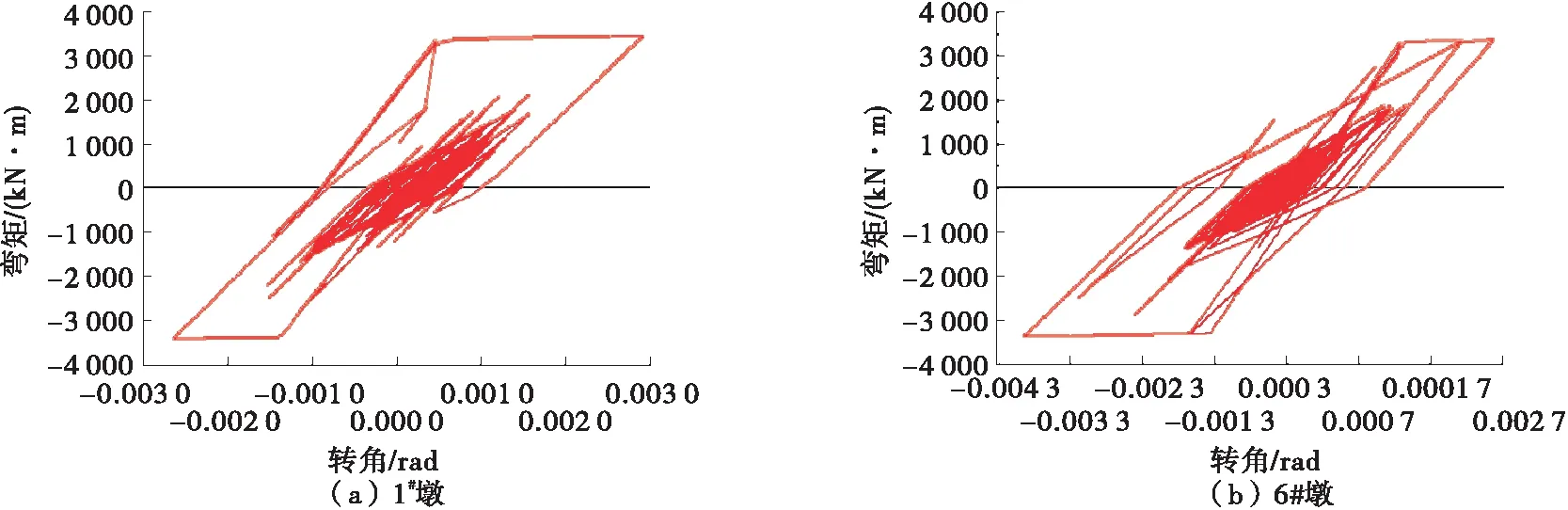
图7 地震波3作用下典型塑性铰滞回曲线

表4 南渡江大桥延性能力与需求对比

地震波1作用下各墩能力/需求指标平均为5.3，地震波2作用下为5.9，地震波3作用下为6.2，各桥墩在不同地震波作用下性能变化较大，说明时程分析结果很大程度上依赖地震波选取。

3.4 结构位移响应分析

3.4.1 桥墩位移安全系数

图8、图9分别为该桥3#墩塑性铰区转角时程曲线和墩顶位移时程曲线。根据《公路桥梁抗震设计细则》进行检算，转角位移和水平位移检算结果分别见表5、表6。

由图8、图9、表5、表6可知：相对于规范值，该桥转角位移和水平位移均较小。塑性铰区转角位移安全系数(θu/θp)为5.25～14.88，墩顶水平位移安全系数(Δu/Δd)为3.68～7.58，结构整体上安全。

3.4.2 结构残余变形分析

从结构位移变化来看，最终质点振动的平衡位置将偏离坐标轴，即产生残余变形，表明塑性变形使结构卸载后不能恢复到原始状态。图10为地震作用后结构典型残余变形。

产生残余变形是延性设计的一个主要缺陷，其大小对结构的震后修复有很大影响。为能从时程曲线中读取有效的残余变形，在地震波数据最后添加一定长度的零加速度，以地震后结构衰减自由振动响应的平均偏移值来评价残余变形。地震波3结束后10 s内，3#墩墩底转角、墩顶位移及上部结构位移见图11和表7、表8。

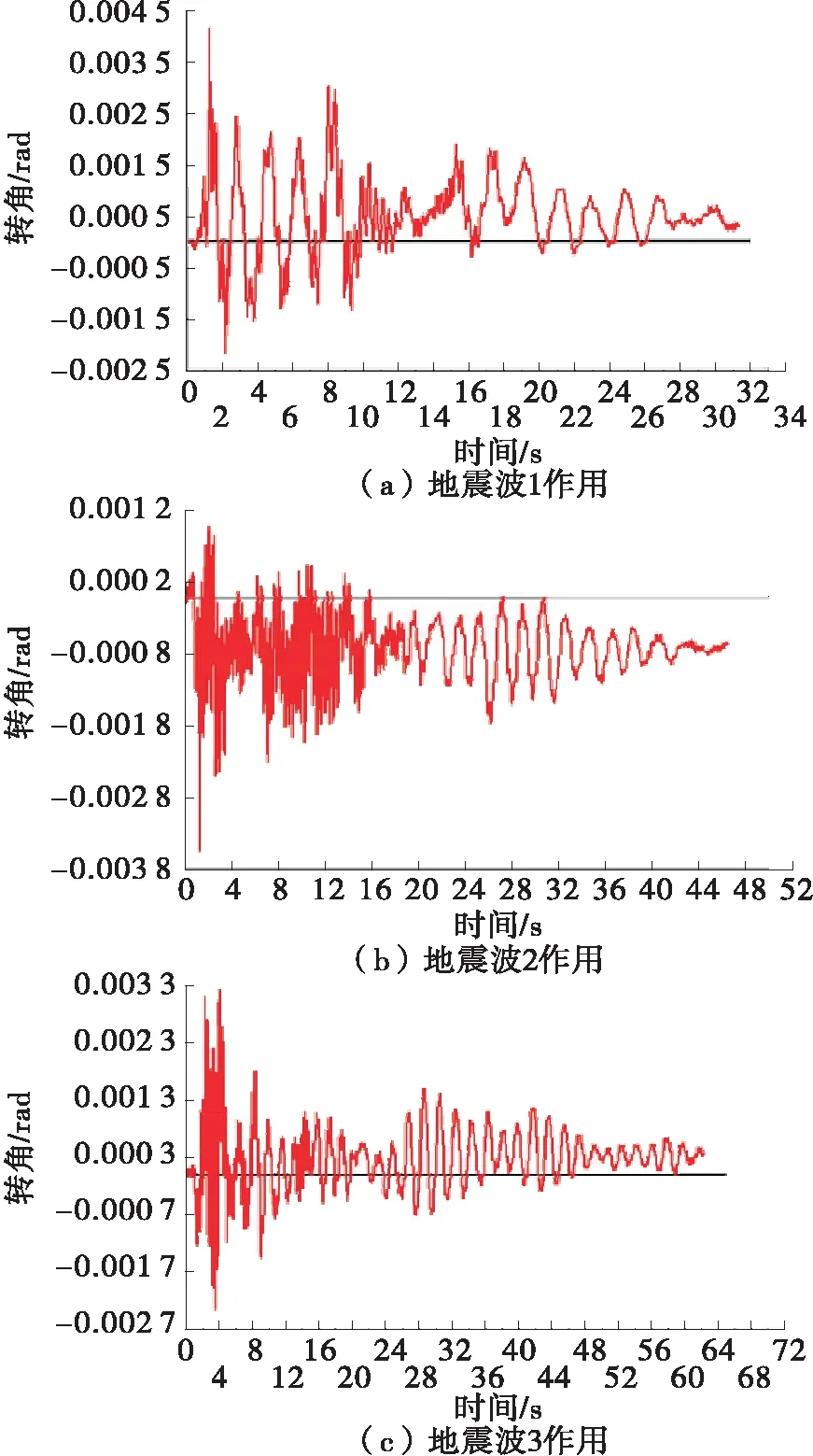
图8 3#墩塑性铰区转角位移时程曲线

图9 3#墩墩顶水平位移时程曲线

表5 转角位移检算结果

表6 水平位移检算结果

图10 地震作用后结构残余变形示意图

由表7、表8可知：墩顶残余位移和上部结构残余位移基本是毫米级，而且其中位移值是偏保守的。从图11曲线变化趋势来看，若继续延长零加速度段，位移平均值将更小。总之，结构残余位移处于可接受范围内。另外，墩顶残余位移比上部结构残余位移大，前者7 mm左右，后者5 mm左右，体现了橡胶支座自复位能力的重要作用。

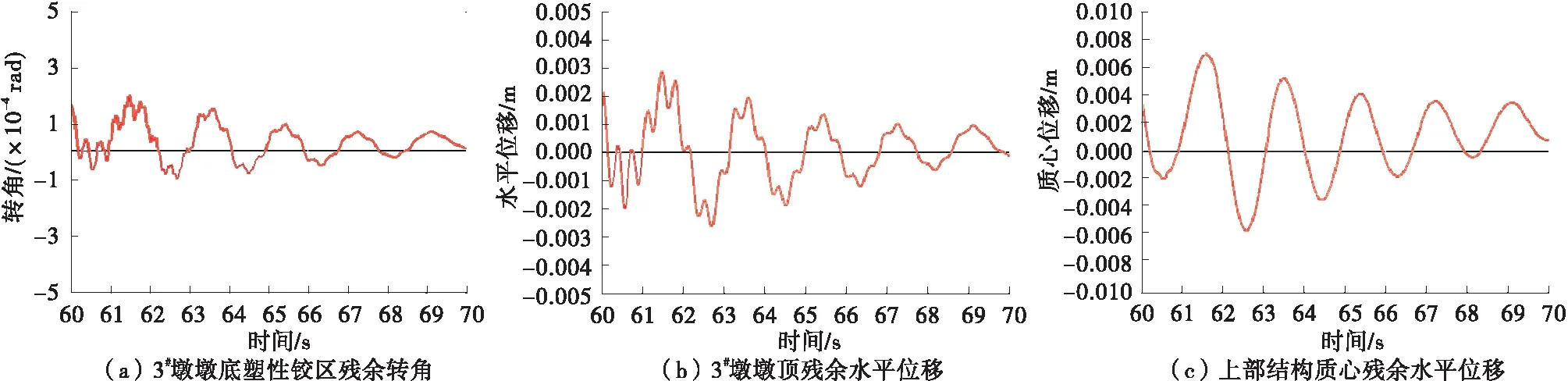
图11 地震波3作用下结构残余位移时程曲线

表7 各墩墩底、墩顶残余变形

表8 上部结构质心残余水平位移m

4 结论

结合工程实例，阐述了弹塑性动力时程分析法的过程，主要结论如下：

(1) 弹塑性动力时程分析结果很大程度上依赖于地震波的选取，随机性很大。

(2) 塑性铰屈服后可调整结构内力分布，使各墩内力趋于均匀。

(3) 对延性构件(桥墩)位移安全系数进行评价，验证了结构的安全性。

(4) 分析了结构残余变形，体现了橡胶支座自复位能力的重要作用。