混合手征活性粒子在时间延迟反馈下的扩散和分离*

廖晶晶 蔺福军

1) (江西理工大学理学院， 赣州 341000)

2) (江西理工大学应用科学学院， 赣州 341000)

3) (华南师范大学物理与电信工程学院， 广州 510006)

在二维空间内， 考虑周期性边界条件， 提出了一种用时间延迟反馈分离混合手征活性粒子的新方法. 当系统引入时间延迟反馈时， 手征活性粒子动力学特征发生明显改变. 通过调节外加时间延迟反馈的强度和反馈时间可以控制逆时针旋转(counterclockwise， CCW)粒子扩散受到顺时针旋转(clockwise， CW)粒子扩散的影响程度. 当时间延迟反馈强度和反馈时间较大且系统参数取最优值时， CCW 粒子加快旋转角速度， 扩散完全由粒子相互作用决定， 而CW 粒子的扩散由自身参数和粒子相互作用共同决定， 在此情况下， CCW 粒子容易聚集形成团簇， 而CW 粒子加快扩散， 混合手征活性粒子实现分离.

1 引 言

生物和物理系统中的活性物质的非平衡特性在理论和实验上已有广泛研究[1-6]. 与被动粒子不同， 活性粒子(也称自驱动力粒子或微泳)能从环境中吸收能量并转化为定向运动. 例如， 自驱动分子马达可以通过消耗活细胞中ATP 水解产生的化学能来进行定向运动[7]， 大肠杆菌通过鞭毛来向前运动[8]等. 当活性粒子结构对称且受到自身驱动力作用时， 它只做线性运动[9]. 如果它受到一个扭矩，则称之为手征活性粒子， 由于自驱动力与驱动方向不在一条直线上， 它将在二维上做圆周运动， 在三维上做螺旋运动[10]. 该类新型活性粒子可以在手征活性流体[11]和许多微生物中找到， 如精子[12]、大肠杆菌[13]及单核细胞增多型李司忒氏菌[14]等.另一方面， 近年来， 受反馈作用的非平衡系统得到了广泛的研究[15-19]. 由于反馈作用， 系统的动力学变得与历史运动有关. 反馈可以通过激光阱[18，20-26]的外部编程(反馈回路[24，27，28])来实现. 此外， 反馈也可能出现在自化学反应粒子中， 即粒子本身是它们所反应的化学物质的产生机制的一部分. 如细菌[29]、兵蚁[30]及合成微粒[31].

混合活性物质的分离技术对于科学和工程研究极为重要[32-55]. 通常对三种类型的混合粒子实现分离. 1)对不同性质的活性粒子混合物的分离.在外加势的作用下， 根据有效扩散系数的不同能够实现两种粒子混合物的分离[33]； 利用离心分离技术或利用非对称障碍物可以分离不同迁移率的自驱动粒子[34，35]； 利用自驱动人工微泳粒子能够实现两种胶体混合物的分离[36]. 此外， Weber 及其合作者[37]研究了粒子间相互作用对相同尺寸不同扩散系数的混合粒子分离的影响， 他们发现仅不同扩散系数就足以驱动两种胶体混合物相分离； Costanzo及其合作者[38]提出了一种在微通道中分离不同迁移率粒子的方法. 2)对主动粒子和被动粒子混合物的分离. Stenhammar 及其合作者[39]研究了主动粒子和被动粒子组成的单分散混合物的相行为和动力学， 结果表明， 主动粒子的运动可以触发相分离. 另外， 在被动粒子和偏心主动粒子的混合体中， 当主动粒子的偏心度足够大时， 偏心粒子可以推动被动粒子形成一个大而密的动态团簇[40].McCandlish 及其合作者[41]实现了在二维空间自由运动的主动粒子和被动粒子的自发分离； Smrek和Kremer[42]的研究发现， 在主动-被动聚合物混合物中， 小的活性差异能驱动相分离. 3)对手征活性物质的分离. 手征活性物质包括多种旋转运动的微生物， 如趋磁细菌[56]、大肠杆菌[57，58]和精子细胞[59]. 手征活性粒子可以根据其运动特性， 在环境中使用一些简单的静态模式来进行分类[45]. Scholz及其合作者[46]研究发现顺时针和逆时针旋转机器人会发生集体运动， 通过调幅分解得到分界面上的超扩散和相分离. 另外， 当系统参数满足一定的关系时， 利用两个相对的旋转障碍物可以分离混合手性粒子[47]. 艾保全等[48]研究表明， 极性手征活性粒子混合物的分离是由手征性和对齐相互作用的竞争决定的.

本文考虑时间延迟反馈作用的影响， 提出一种手性分离的新方法. 通常情况下， 单纯考虑粒子之间排他相互作用， 手征活性粒子混合物并没有自分离特性， 但时间延迟反馈和输出信号之间的差值能重新作用到系统， 改变系统的运动状态， 实现对混合粒子手征性和扩散特性的差异性调制， 相当于给系统提供一种可调节的外驱动. 具体来说， 当时间延迟反馈强度和反馈时间均很大且系统参数取最优值时， 逆时针旋转(counterclockwise， CCW)粒子快速旋转， 扩散完全由粒子相互作用控制， 顺时针旋转(clockwise， CW)粒子扩散由自身参数和粒子相互作用共同决定， 因此粒子分离； 当两种粒子扩散都由自身参数和粒子相互作用共同决定时，粒子无法分离. 通过调节反馈强度和反馈时间可以调节不同手性粒子的扩散控制因素， 从而达到粒子分离的目的.

2 模型和方法

考虑半径为r的手征活性粒子混合物(N/2个CCW 粒子，N/2 个CW 粒子)在尺寸为L×L，满足周期边界条件的二维空间中运动. 粒子除了受到排斥相互作用， 还受到时间延迟反馈作用[60]. 粒子的运动由质心位置ri ≡(xi,yi) 和极坐标ni ≡(cosθi,sinθi) 下的角度θ描述. 角度由旋转扩散、作用在粒子上的常数扭矩及相邻粒子间的相互作用决定. 考虑平动和转动扩散系数不相关且平动扩散系数可忽略的情况下， 描述过阻尼下粒子动力学性质的郎之万方程为

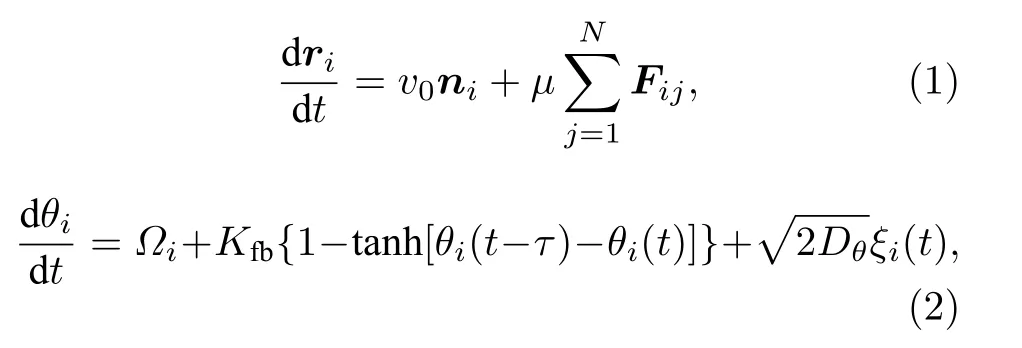
其中v0是自驱动速度，µ为迁移率.Dθ是转动扩散系数，ξi(t) 是零平均单位方差高斯白噪声. 角速度Ωi=±ω的符号决定了粒子的手征性，Ωi ＞0 代表粒子逆时针旋转，Ωi ＜0 代表粒子顺时针旋转.

粒子之间采用短程谐波相互作用： 当rij ＜2r时，否则，是粒子i和粒子j间的相互作用距离.此处k为弹性系数. 为了模拟硬粒子， 使用较大的弹性系数， 令µk=100 ， 保证粒子不重叠.Kfb是反馈的强度，τ是反馈时间. 其中，Kfb≥0 ，τ≥0 ，0 ≤Ω(t)≤2Kfb. 这种反馈机制引入了一个时间间隔为τ的逆时针扭矩作用在粒子上(如图1).

为了描述两种粒子的空间分布， 将系统分隔成M个 (L×L)/M的区块， 分离系数则定义为[61]

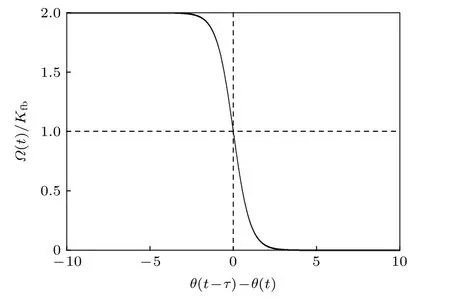
图1 时间延迟反馈示意图. 当 τ =0 时， Ω (t)=Kfb ； 当τ →∞ 且 θ (t−τ)＞θ(t) 时， Ω (t)=0 ； 当 τ →∞ 且θ(t−τ)＜θ(t) 时，Ω(t)=2KfbFig. 1. Schematic diagram of time-delayed feedback. When τ =0 ， Ω (t)=Kfb ； when τ →∞ and θ (t −τ)＞θ(t) ，Ω(t)=0 ； when τ →∞ and θ (t −τ)＜θ(t) ， Ω(t)=2Kfb.

为了描述混合物中单种粒子团簇的特征尺寸，定义相对径向分布函数[46，50]：

定义所有粒子所占的面积与二维系统面积的比例为填充率φ=Nπr2/(L×L) . 引入时间尺度和长度尺度r对参数进行无量纲化：在以下讨论中均使用无量纲量且省略所有量上面的“帽子”， 通过改变角速度ω，反馈强度Kfb， 反馈时间τ， 转动扩散系数Dθ和自驱动速度v0来研究系统的行为. 粒子在二维空间的有效扩散系数为

其中 Δri(t)≡ri(t)−ri(0) .

3 结果和讨论

在模拟中， 粒子的初始位置随机分布， 且方向角在 [ 0,2π] 上是随机的. 利用龙格库塔算法对方程(1)和(2)进行数值积分. 积分步长小于 1 0−3， 总积分时间大于 2×104(该积分时间可以确保系统达到稳态). 进行了100 次数值计算以提高计算精度和减小统计误差. 模拟参数选取为L=40.0 ，M=10×10=100，N=1024 (φ=0.50 ).

对于手性活性粒子混合物， 自驱动方向角度θ由ω，Dθ，Kfb，τ决定. 角速度ω决定了手征性差异(当ω=0.0 时， 两种粒子是无差异的). 转动扩散系数Dθ描绘了角速度的波动. 当Dθ固定时， 粒子的扩散由ω，v0，Kfb及τ的竞争决定.

图2 CCW 粒子(红色)和CW 粒子(蓝色)的混合物分布 (a) K fb =0, ω =0 ； (b) K fb =10.0, τ =10.0, ω =0 ；(c) K fb=10.0,τ=10.0,ω=2.2 ； (d)Kfb =10.0, τ =10.0,ω =4.2 . 其他参数设 置为 v 0 =2.5 ， D θ = 0 .001 ，φ=0.5Fig. 2. The snapshots of mixture of CCW particles (red)and CW particles (blue)： (a) K fb =0,ω =0 ； (b)Kfb =10.0,τ =10.0,ω =0 ； (c) K fb =10.0,τ =10.0,ω =2.2 ；(d) K fb =10.0,τ =10.0,ω =4.2 . The other parameters are v 0 =2.5 ， D θ =0.001 ， and φ =0.5 .

图2 描述了混合手征活性粒子在v0=2.5 ，Dθ=0.001 ，φ=0.5 ，ω和Kfb及τ不同时的粒子分布图. 可得： 1) 当Kfb=0 ，ω=0 时(如 图2(a))，两种粒子无差别且不受时间延迟反馈作用， 粒子由于自驱动作用聚集成团， 发生自驱动诱导相分离(MIPS， motility induced phase separation)现象[62].2) 当Kfb=10.0 ，τ=10.0 ，ω=0 时(如 图2(b))，两种粒子相同且受到强的时间延迟反馈作用， 粒子受到大的扭矩作用， 因此反馈调制后的角速度很大， 旋转半径(R=v0/ω)很小， 粒子几乎待在原地打转， 从整体上看， 粒子是均匀分布且混合的.3) 当Kfb=10.0 ，τ=10.0 ，ω=2.2 时(如图2(c))，手征差异性增加， 由于时间延迟反馈作用， 使得CCW 粒子的角速度增大， 旋转半径减小(∝1/ω)，扩散减小. 对CW 粒子， 反馈对其几乎无作用， 因此 以ω=2.2 的角速度CW 转 动， 旋转半径较CCW 粒子的旋转半径更大， 扩散较大. 由于排他相互作用， 一方面CW 粒子在与CCW 粒子相互作用的过程中从CCW 粒子中挣脱逃逸， 另一方面推进CCW 粒子聚集成一个团簇整体旋转， 两种粒子分离； 4) 当Kfb=10.0 ，τ=10.0 ，ω=4.2 时(如图2(d))， 粒子角速度ω增大， 由于延迟时间反馈作用， CCW 粒子角速度进一步增大， 旋转半径减小；但时间延迟反馈对CW 粒子几乎无作用， 因此CW 粒子基本保持原角速度旋转， 但旋转半径变小， 扩散减小， 因此一方面很难从CCW 粒子中挣脱逃逸， 另一方面只能在小区域推进CCW 粒子聚集， 所以在每一个小区域， 两种粒子分离， 但是整体上来说， 较小的团簇出现， 粒子混合.

为了研究团簇大小， 使用CW 粒子和CCW粒子的最大团簇粒子数占各自总粒子数的比例P=〈Ncl〉/(N/2) 随角速度ω的变化如图3(a)中描述.Ncl为最大团簇的粒子数个数.P越大代表团簇尺寸越大， 表明粒子分离. 由图可知， 比例P是角速度ω的峰值函数. 图中a， b， c 及d 四点的分布图分别对应图2(a)，图2(b)， 图2(c)及图2(d). 由图3(a)可以看出， 1) 当ω=0 时(a， b 点)， CW 粒子和CCW 粒子的最大团簇强度P相等. 当Kfb=0时， 由于MIPS 效应， 最大团簇强度比例P=0.8 ； 当Kfb=10.0 ，τ=10.0 ，ω=0 时， 两 种粒子均做逆时针旋转且旋转半径很小， 几乎各自待在 原 地 打 转， 因 此P=0 . 2) 当ω=2.2 时(c 点)时， 在外加时间延迟反馈作用下， CW 粒子角速度不变， CCW 粒子角速度增大， 在两种粒子相互作用下， CCW 粒子聚集成一大团簇，P接近于1， 达到最大值； CW 粒子旋转半径更大， 扩散更大， 聚集成小团簇，P≃0.2 . 3) 当ω=4.2 时(d 点)， CCW角速度继续增大， CW 粒子旋转半径继续减小， 均聚集成更小团簇. 图3(b)绘制了不同ω下，Kfb=10.0 ，τ=10.0 ，t=2×104时， 相对径向分布函数gAB(r) .图中标注的圆圈为第一个零根， 代表单种粒子的团簇尺寸. 当ω=0.0 和 5.4 时， 顺时针和逆时针粒子旋转角速度都很大， 旋转半径很小， 所以团簇尺寸很小； 随着ω增加， 反馈加速CCW 粒子旋转， 对CW 粒子无作用， 逆时针旋转角速度很大， 顺时针旋转角速度很小， 团簇尺寸增大， 当ω=2.2 时， 团簇尺寸达到最大值.

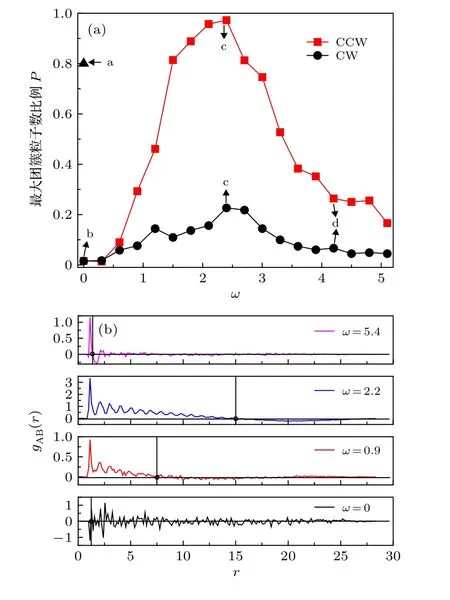
图3 (a) CW 粒子和CCW 粒子的最大团簇粒子数占各自总粒子数的比例P 随角速度 ω 的变化. 图中a， b， c， d 四点的构型图分别对应图2(a)， 图2(b)， 图2(c)， 图2(d)； (b)在不同 ω 下， t =2×104 时， 相对 径向分 布函数 g AB(r) . 图中标注的圆圈为第一个零根， 代表单种粒子的团簇尺寸. 其他参数设置为 v 0 =2.5 ， D θ =0.001 ， φ =0.5 ， K fb =10.0 ，τ =10.0Fig. 3. (a) The ratio of the particle number in maximum cluster of CW particles and CCW particles to the total number of particles respectively as a function of ω . The points a， b， c， d are corresponding to Fig. 2(a)，Fig. 2(b)，Fig. 2(c)，Fig. 2(d)， respectively； (b) relative radial distribution function g AB(r) for different value of ω at t =2×104 . The first non-trivial root (marked by circles) denotes the cluster size of the single particle species. The other parameters are v0 =2.5 ， D θ =0.001 ， φ =0.5 ， K fb =10.0 ， and τ =10.0.

为了进一步描述粒子动力学， 分别研究了有效扩散系数D和分离系数S随角速度ω， 反馈强度Kfb， 反馈时间τ， 转动扩散系数Dθ， 自驱动速度v0，填充率φ和时间t的变化. 图4—图10 中的每条曲线均是由100 次模拟的统计平均得到的.

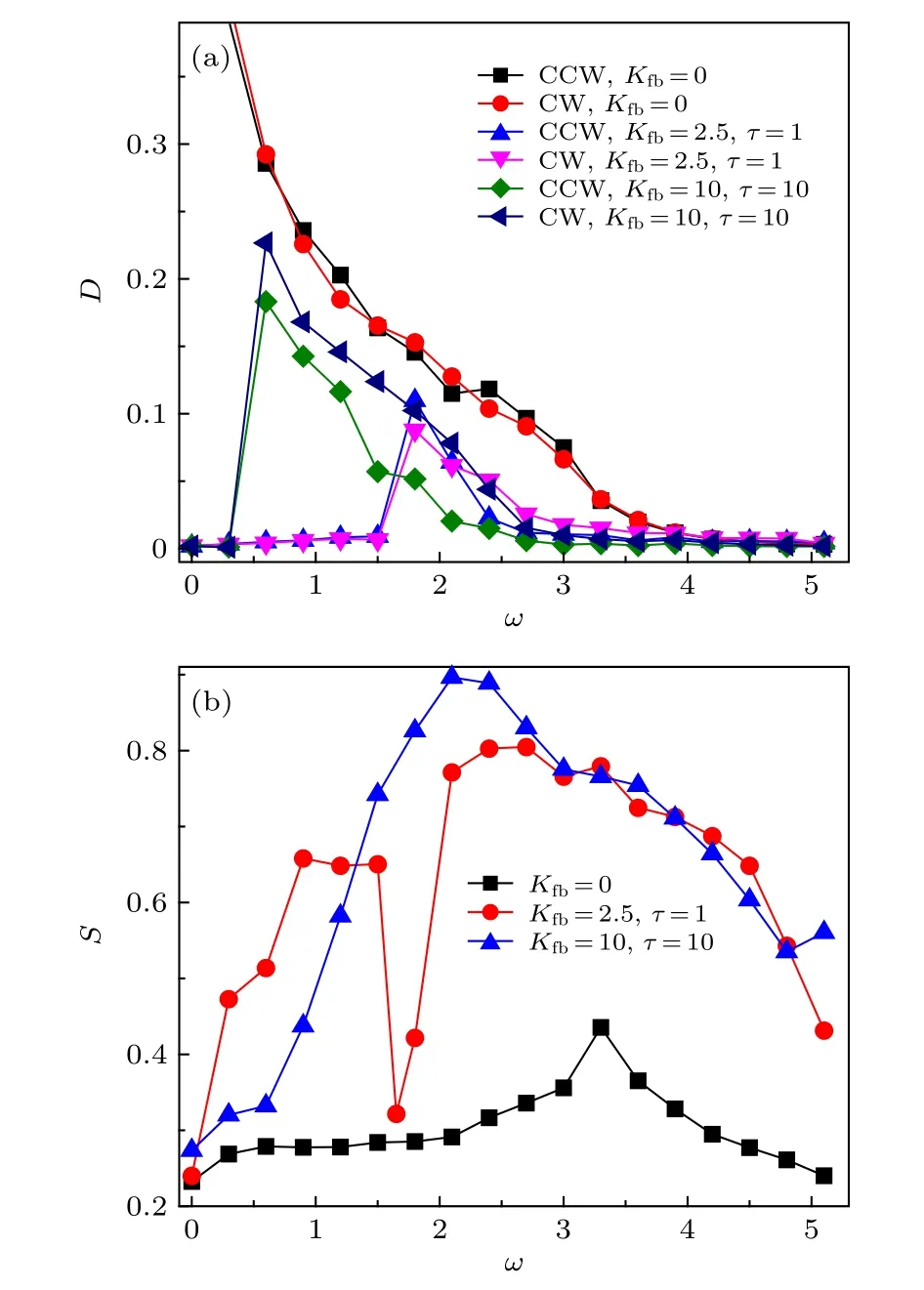
图4 (a)在不同 K fb 和 τ 值下， CCW 粒子和CW 粒子 的有效扩散系数D 随角频率 ω 的变化； (b)在不同 K fb 和τ下， 分离系数S 随角频率 ω 的变化. 其他参数设置为v0 =2.5， D θ =0.001 ，φ=0.5Fig. 4. (a) The effective diffusion coefficient D of CCW and CW particles as a function of ω for different K fb and τ ；(b) the separation coefficient S as a function of ω for different K fb and τ . The other parameters are v 0 =2.5 ，Dθ =0.001 ， and φ =0.5 .

图4 研究了在不同Kfb和τ值下， CCW 粒子和CW 粒子的有效扩散系数D和分离系数S随角速度ω的变化. 从图4(a)可知， 当Kfb=0 时， 粒子不受反馈作用， CCW 和CW 粒子的有效扩散系数D相等， 且随ω单调减小； 而当Kfb和τ取其他值时， CCW 粒子和CW粒子的有效扩散系数为ω的峰值函数. 可以解释如下： 1) 当Kfb=0 ，ω=0时， 粒子自身参数(自驱动速度， 转动扩散系数等)控制扩散， 扩散远远大于1， 达到最大值； 2) 当Kfb=0 ，ω→∞时， 粒子转动非常快， 自驱动速度可忽略，D→0 ； 3) 当Kfb和τ取其他值，ω→0 时，两种粒子相同， 时间延迟反馈使得粒子快速旋转，D →0 . 随着ω增加， 时间反馈对两种粒子角速度调制差异开始显现， 由图1 可知，τ越大， CCW 粒子受到反馈作用后ω增大越多， CW 粒子的ω受到的调制越小， 当τ很大时， CCW 粒子和CW 粒子受到的扭矩调制作用分别趋于 2Kfb和0.ω的增加能导致两种结果： (A) 两种粒子手征差异性增大，粒子相互作用力增大， 扩散增大； (B)抑制自驱动，减小扩散. 当ω从零增加， A 因素控制扩散， 扩散主要由粒子间相互作用控制，ω越大， 受到 的CW 粒子的排斥力越大，D越大； 而CW 粒子扩散主要由自身参数决定(受反馈影响很小)， CW 粒子的D随ω增加而增加. 当ω继续增加， B 因素起作用， CW 粒子快速旋转， CW 的扩散趋于0， 因此CCW 粒子受到CW 粒子的排斥力作用效应越来越小， CCW 扩散也趋于0. 值得注意的是，Kfb=10 ，τ=10 时 的D大于Kfb=2.5,τ=1 时的D且峰值对应的ω更小. 此外， 当Kfb=10 ，τ=10时， CW 粒子有效扩散大于CCW 粒子的有效扩散； 而Kfb=2.5 ，τ=1 时， CW粒 子有效扩散在1.7＜ω ＜2.1时小于CCW 粒子的有效扩散， 在ω ＞2.1 时 ， CW 粒子的D更大. 这是因为Kfb和τ越大， 时间延迟反馈对粒子角速度调制作用越强，导致CCW 粒子和CW 粒子角速度差异越大， CCW粒子扩散由CW 粒子排斥力决定的程度越大.

由图4(b)发现， 分离系数S为角速度ω的峰值函数. 当ω→0 时， 两种粒子相同， 且扩散都由粒子参数和相互作用共同控制， 粒子混合，S→0 ； 当ω →∞时，ω控制了粒子运动， 两种粒子都快速旋转， 几乎各自待在原地打转，S→0 . 所以ω取最优值时， 分离系数能达最大值. 峰值位置随Kfb和τ增大而往ω减小方向移动. 当Kfb=10,τ=10 时的分离效果最好， 这是因为此时CCW 粒子角速度受时间延迟反馈调制快速逆时针旋转， 其扩散与自身参数无关， 完全由CW 粒子的扩散决定. 特别地， 当Kfb=2.5,τ=1时， 曲线存在一个谷底值. 这是因为ω＞1.65 时， CW 粒子顺时针旋转； 而ω ＜1.65时， CW 粒子被时间延迟反馈调制为逆时针旋转.|ω −1.65|越大， CCW 粒子扩散受CW 粒子扩散影响程度越大， 因此ω=1.65 时，S达最小值.

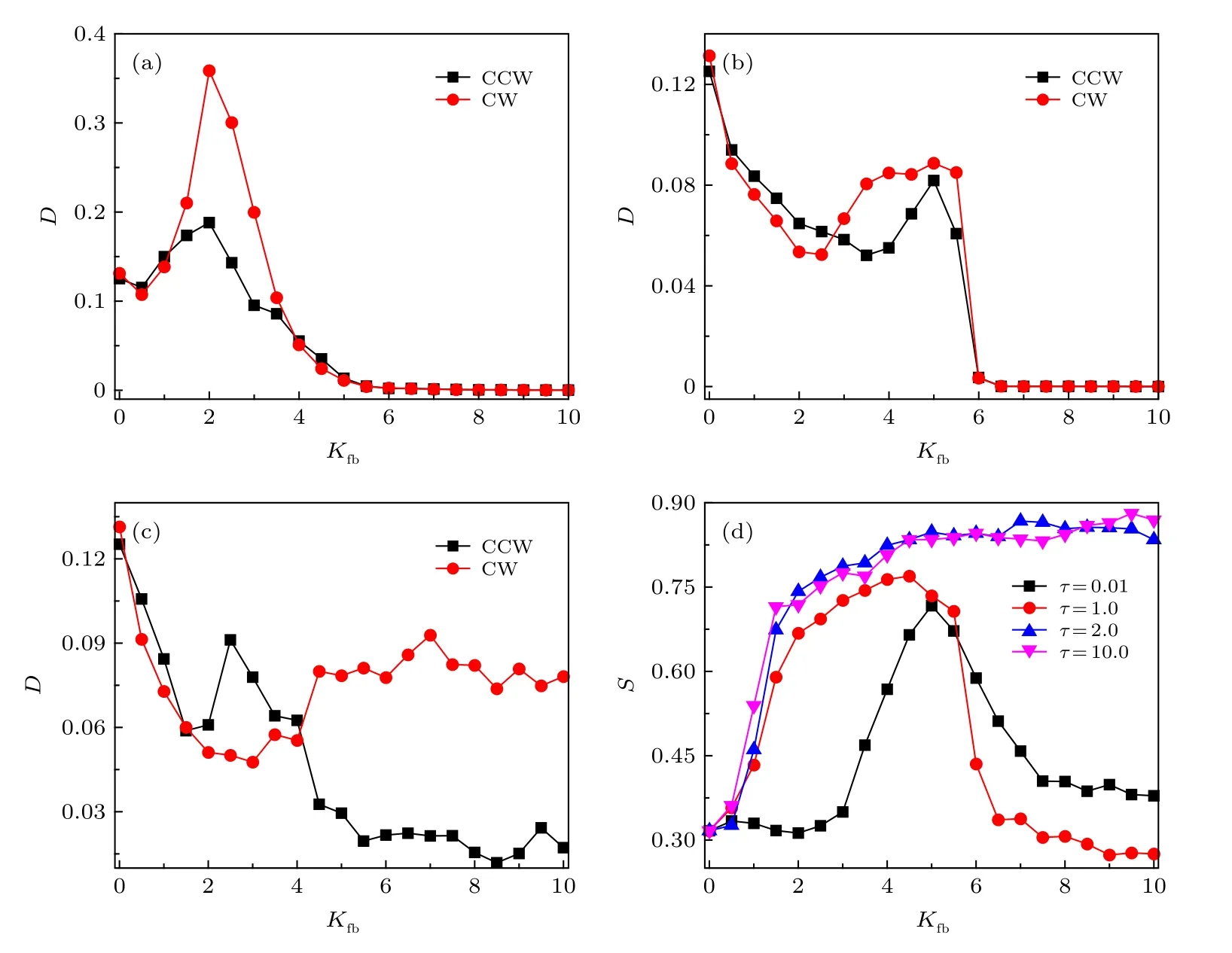
图5 在 (a) τ =0.01 ， (b) τ =1.0 ， (c) τ =10.0 时， CCW 粒子和CW 粒子的有效扩散系数D 随反馈强度 K fb 的变化； (d)在不同 τ 下， 分离系数S 随反馈强度 K fb 的变化. 其他参数设置为 ω =2.1 ， v 0 =2.5 ， D θ =0.001 ，φ=0.5Fig. 5. The effective diffusion coefficient D of CCW and CW particles as a function of K fb at (a) τ =0.01 ， (b) τ =1.0 ， and(c) τ =10.0 ； (d) the separation coefficient S as a function of K fb for different τ . The other parameters are ω =2.1 ， v 0 =2.5 ，Dθ =0.001 ， and φ =0.5 .

图5 描绘了在不同τ值下， CCW 粒子和CW 粒子的有效扩散系数D和分离系数S随反馈强度Kfb的变化. 可以看出， 1) 当τ=0.01 时， 两种粒子的D为反馈强度的峰值函数(如图5 (a)).Kfb很小时， 外加反馈对粒子角速度调制作用很小，CCW 粒子和CW 粒子扩散相等且由自身参数控制； 随Kfb增大， 调制作用增大， 由于τ很小， 反馈作用在CCW 粒子和CW 粒子的扭矩几乎相等，CW 粒子调制后角速度减小，D增大， 当Kfb≈2.1时达到最大值， 此时CW 粒子角速度几乎为0， 而CCW 粒子调制后角速度增大，D受CW 粒子扩散影响增大， 因此也在Kfb≈2.1 时达到最大； 当Kfb→∞时， 两种粒子调制后角速度很大，D→0 .2) 当τ=1.0 (如图5 (b))时， 随Kfb增加， 两种粒子扩散先减小， 后增大达到最大值，Kfb→∞时，D →0 . 3) 当τ=10.0 (如图5 (c))时，D随Kfb先减小， 后增大达到最大值， 继而趋于常数， 这是因为此时CW 粒子几乎不受反馈调制作用，Kfb的改变对D无影响， 而CCW 粒子的扩散完全由CW 粒子对CCW 粒子的排斥力控制， 因此也趋于常数且小于CW 的扩散. 由图5(d)可知，τ≤1 时，分离系数S为反馈强度Kfb的峰值函数， 而τ ＞1时，S随Kfb的增大而增大并于Kfb=10 时达到最大值并保持不变. 可以解释如下： 1) 当τ≤1 时， 外加反馈对CW 粒子调制随Kfb增大而改变， 当Kfb从零开始增加， CW 粒子为顺时针旋转， 且随Kfb增加角速度减小， 扩散增大， CCW粒子扩散受CW 粒子扩散影响程度增大，S达最大值， 粒子分离； 随着Kfb继续增大， CW 粒子由顺时针旋转翻转为逆时针旋转， 与CCW 粒子同时受外加反馈强烈调制， 两种粒子扩散由各自自身参数决定， 因此S降低， 粒子混合. 2) 当τ＞1 时， CW 粒子几乎不受外加反馈作用， 因此CW 粒子扩散不随Kfb而改变， CCW 粒子扩散受CW 粒子扩散影响程度越来越大， 当Kfb=10 时， CCW 粒子扩散完全由CW 粒子扩散决定， 所以S达到峰值并且保持不变. 可以通过控制外加时间反馈强度来控制不同手征性粒子的扩散和分离.

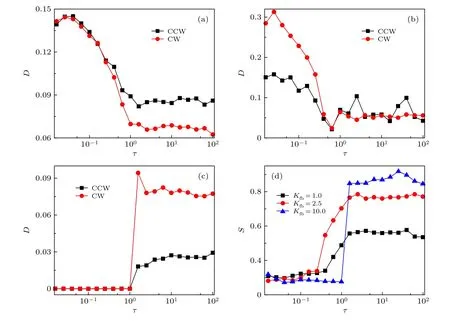
图6 在(a) K fb =1.0 ， (b) K fb =2.5 ， (c) K fb =10.0 时， CCW 粒子 和CW 粒子的有效扩 散系数D 随反馈时间 τ 的变化； (d) 在不同 K fb 下， 分离系数S 随反馈时间 τ 的 变化. 其他 参数设置为 ω =2.1 ， v 0 =2.5 ， D θ =0.001 ，φ=0.5 Fig. 6. The effective diffusion coefficient D of CCW and CW particles as a function of τ at (a) K fb =1.0 ， (b) K fb =2.5 ， and(c) K fb =10.0 ； (d) the separation coefficient S as a function of τ for different K fb . The other parameters are ω =2.1 ， v 0 =2.5 ，Dθ =0.001 ， and φ =0.5 .

图6 描述了在不同Kfb值下， CCW 粒子和CW粒子的有效扩散系数D和分离系数S随反馈时间τ的变化. 可以看出： 1) 当Kfb很小时 (Kfb=1.0,2.5 )，两种粒子的D随反馈时间τ的增加而先增加， 后单调减小， 且在τ＞1 时达到平稳值(如图6(a)和6(b)). 这是因为当τ＜1 时， CCW 粒子受外加反馈调制强度随τ增加而增加， 而CW 粒子受调制强度随τ增加而减小， 所以两种粒子的扩散都随τ增加而单调减小； 2) 当τ＞1 时， CCW 粒子受外加反馈调制强度随τ增加而急剧增加， 扩散主要来自与CW 粒子的相互作用力， 而CW 粒子不受调制强度影响， 因而扩散不随τ变化， CW 粒子扩散决定了粒子间的相互作用力， 所以CCW 粒子扩散也保持常数. 当Kfb很大时(Kfb= 1 0.0 )， 两种粒子的D随反馈时间τ的增加而先保持为0， 后在τ=1 时突然增大并保持为常数(如图6(c)). 可以解释如下： 1) 在τ＜1 时， CW 粒子在外加反馈作用下由顺时针旋转翻转为逆时针旋转， 并且角速度值很大， 所以两种粒子扩散都几乎为0； 2) 在τ＞1 时，CCW 粒子受外加反馈作用快速旋转， 其扩散主要来自粒子间的相互作用力， CW 粒子保持原有的角速度， 扩散保持常数不变， 因而CCW 粒子扩散比CW 扩散低且保持不变. 由图6(d)可发现， 分离系数S随τ的增加而增加并于τ＞1 后保持不变. 其中Kfb=1.0,2.5 时，S随τ缓慢增加， 而Kfb=10.0时， 分离效果最好且S在τ=1 时突然增大到最大值， 这与图5(d)结果一致. 这是因为τ＞1 时，CCW 粒子扩散完全由不随τ变化的CW 粒子扩散控制.

在不同Kfb和τ值下， CCW 粒子和CW 粒子的有效扩散系数D和分离系数S随转动扩散系数Dθ的变化如图7 所示. 由图7(a)—图7(c)可以发现， 有效扩散系数D随Dθ先增大， 后减小， 继而增大， 出现一个谷底和一个峰值， 最后Dθ →∞时，D →0 . 这是由于随Dθ增大过程中， 在外加反馈调控下， 粒子调制后的角速度与Dθ竞争造成的， 当调制后的角速度很小时，Dθ控制粒子的扩散， 当调制后的角速度很大时，Dθ的作用可以忽略. 当Dθ →∞时， 粒子完全由Dθ控制， 粒子自驱动角度θ变化很快， 所以D→0 . 图7(d)可以看出， 分离系数S随转动扩散系数Dθ的增加而单调递减，Kfb=10.0 ，τ=10.0 时S取最大值， 这与前面的结果一致. 当Dθ →0 时， 转动扩散系数可以忽略， 因此S达最大值.

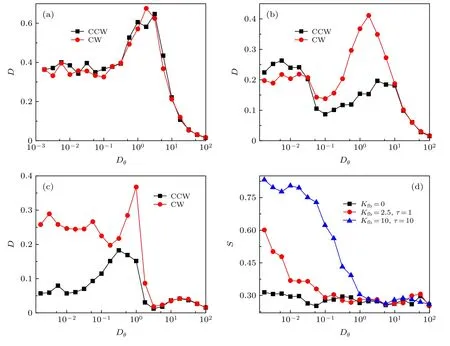
图7 在(a) K fb =0.0 ， (b) K fb =2.5,τ =1.0 ， (c) K fb =10.0,τ =10.0 时， CCW 粒子和CW 粒子的 有效扩散 系数D 随 转动扩 散系数 D θ 的变化； (d) 在不同 K fb 和 τ 下， 分 离系数S 随 转动扩散系数 D θ 的变化. 其他参数 设置为 ω =2.1 ， v 0 =2.5 ，φ=0.5Fig. 7. The effective diffusion coefficient D of CCW and CW particles as a function of D θ at (a) K fb =0.0 ， (b)Kfb =2.5,τ =1.0 ， and (c) K fb =10.0,τ =10.0 ； (d) the separation coefficient S as a function of D θ for different K fb and τ . The other parameters are ω =2.1 ， v 0 =2.5 ， and φ =0.5 .

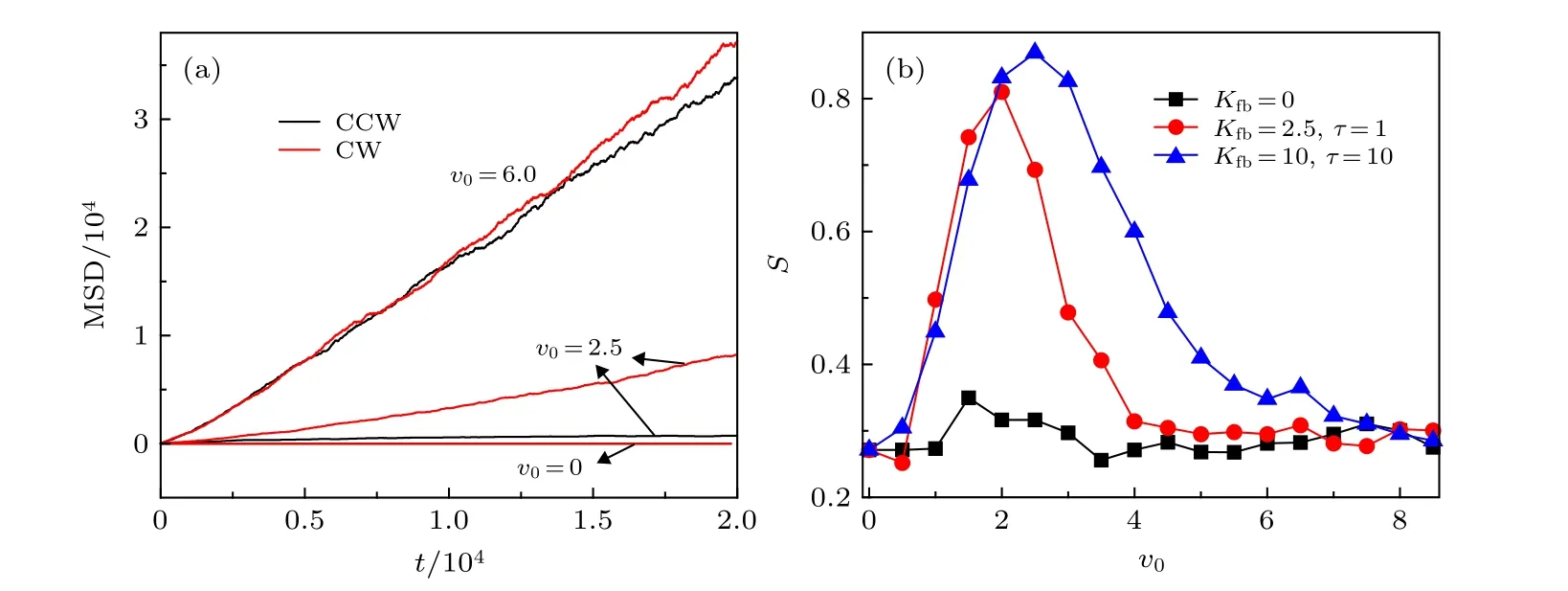
图8 (a)在 K fb =10.0 ， τ =10.0 时， 不同自驱动速度 v0 下， 均方位移 随时间t 的变化； (b)在不同 K fb 和τ下， 分离系数S 随自驱动速度 v 0 的变化. 其他参数设置为 ω =2.1 ， D θ =0.001 ，φ=0.5Fig. 8. (a) The mean square displacement as a function of t for different v0 at K fb =10.0 and τ =10.0 ； (b)the separation coefficient S as a function of v0 for different K fb and τ . The other parameters are ω =2.1 ， D θ =0.001 ， and φ=0.5.

图8 (a)绘 制 了 在Kfb=10.0 ，τ=10.0 时， 不同自驱动速度v0下， 均方位移随时间t的变化. 可以看出， 1) 当v0=0 时， 两种粒子扩散完全由角速度控制， 因此MSD 始终趋于0. 2) 当v0= 2.5 时， CCW 粒子快速旋转， MSD完全由CW 粒子的MSD 决定， CW 粒子的MSD由自驱动速度v0和角速度ω共同决定， 且随时间t增大， 所以CCW 粒子的MSD 也随时间t增大，且小于CW 粒子的MSD. 3) 当v0=6.0 ， 两种粒子的MSD 都由v0和角速度ω共同决定， 因此两种粒子的MSD 随时间t增大且交叉多次. 图8(b)描述了在不同Kfb和τ下， 分离系数S随自驱动速度v0的变化. 图形显示为铃铛状， 这是由于单个手征粒子做旋转运动的半径为R=v0/ω， 当v0→0 时，粒子待在各自位置做自旋运动， 因此S趋于零. 当v0→∞时， 两种粒子扩散都由v0和ω共同决定， 粒子混合，S→0 . 所以存在最优值v0使得分离系数S达到最大值.

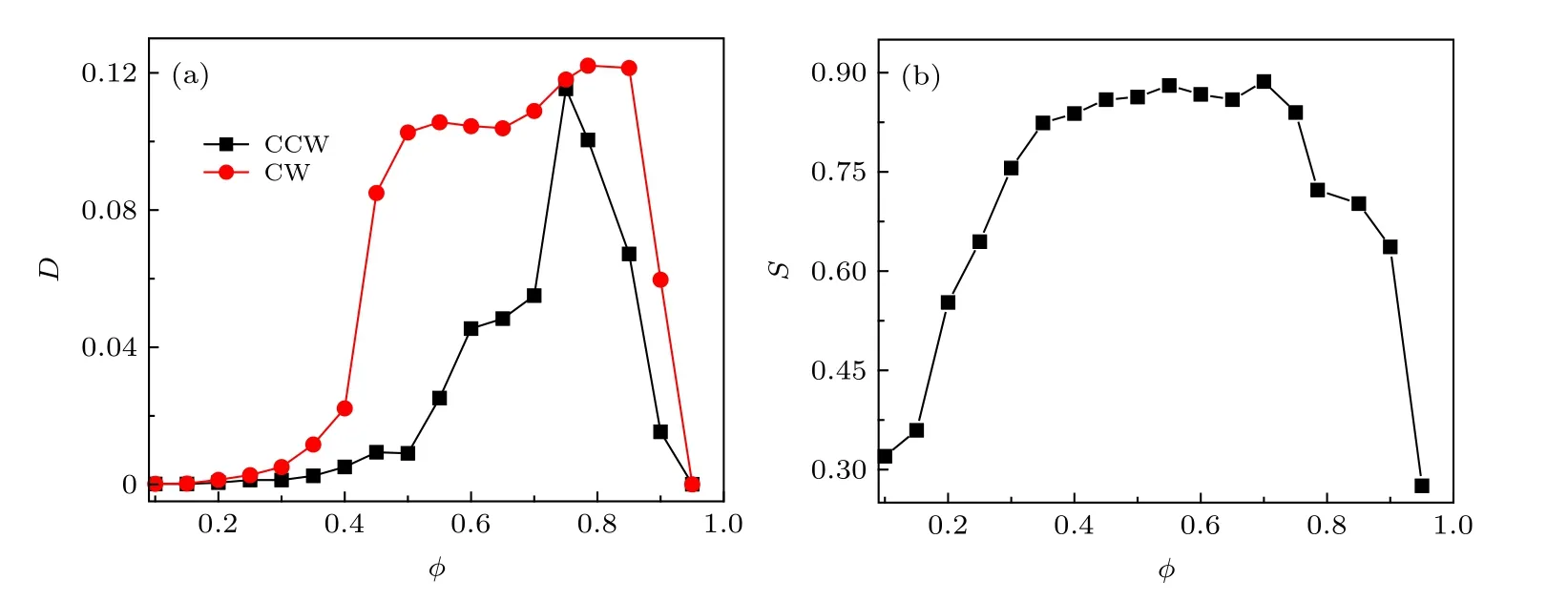
图9 (a) CCW 粒子和CW 粒子的有效扩散系数D 随填充率 φ 的变化； (b) 分离系数S 随填充率 φ 的变化. 其他参数设置为v0 =2.5 ， D θ =0.001 ， ω =2.1 ， K fb =10.0 ，τ =10.0Fig. 9. (a) The effective diffusion coefficient D of CCW and CW particles as a function of φ ； (b) the separation coefficient S as a function of φ . The other parameters are v 0 =2.5 ， D θ =0.001 ， ω =2.1 ， K fb =10.0 ， and τ =10.0 .

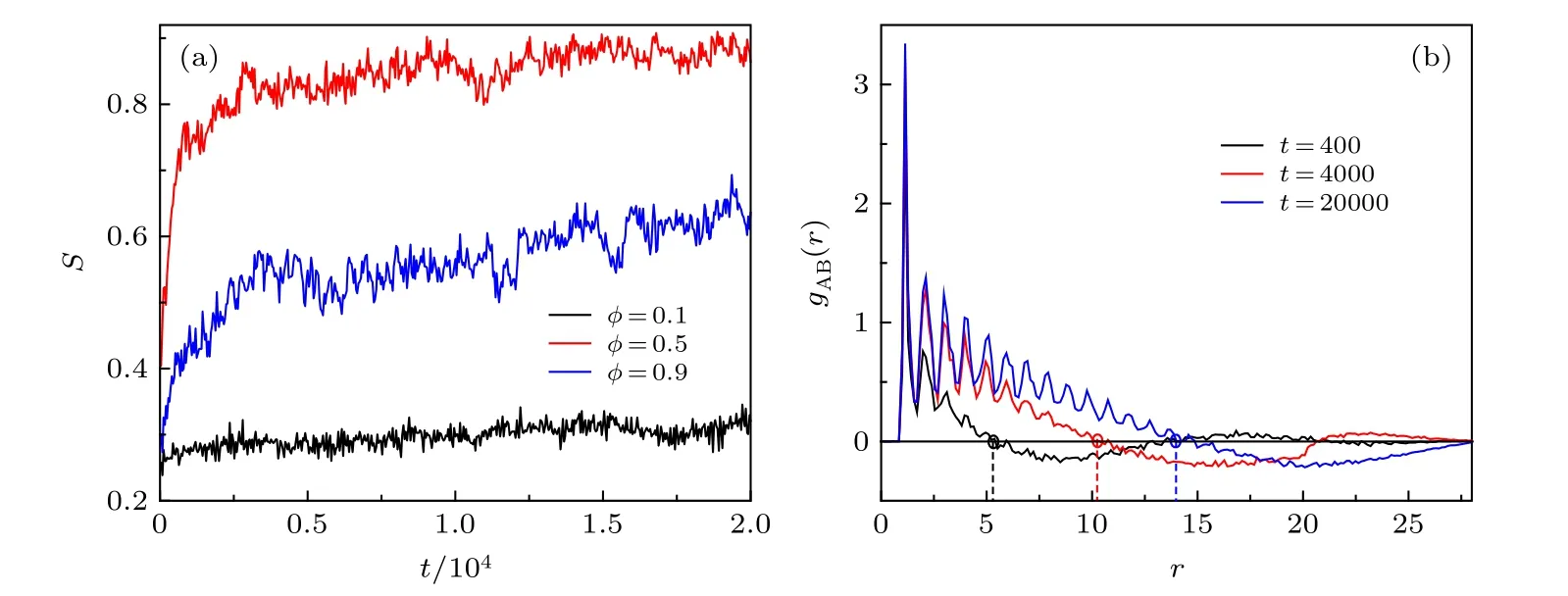
图10 (a)在不同填充率 φ 下， 分离系数S 随时间t 的变化； (b)在不同时间t 下， φ =0.5 时， 相对径向分布函数 g AB(r) . 图中标注的圆圈为第一个零 根， 代表单 种粒子的团簇尺寸. 其他参数设置为 v 0 =2.5 ， D θ =0.001 ， ω =2.1 ， K fb =10.0 ，τ =10.0Fig. 10. (a) The separation S as a function of t for different φ ； (b) the relative radial distribution function g AB(r) for different t at φ=0.5. The first non-trivial root (marked by circles) denotes the cluster size of the single particle species. The other parameters are v 0 =2.5 ， D θ =0.001 ， ω =2.1 ， K fb =10.0 ， and τ =10.0 .

图9 (a)和图9(b)分别描述了CCW 粒子和CW 粒子的有效扩散系数D和分离系数S随填充率φ的变化. 可以看出， 有效扩散系数D和分离系数S都表现为填充率φ的峰值函数. 当φ很小时，粒子间的平均距离很大， 发生相互作用的概率很小， 导致D很小， 粒子无法聚集， 因此分离系数S也很小. 当φ很大时， 粒子间相互作用变得重要，粒子拥挤造成粒子很难移动， 所以D很小，S也很小. 所以存在最优值φ使得有效扩散系数D和分离系数S达到最大值.

为了验证模拟结果具有鲁棒性， 绘制了在不同填充率φ下， 分离系数S随时间t的变化， 如图10(a)所示. 选取的积分时间大于 2×104， 由图10(a)可知， 分离系数S从t=1×104开始保持常数不变，即系统达到稳态. 此外φ=0.5 的分离系数最大， 这与图9(b)结果一致. 图10(b)描述了在不同时间t下，φ=0.5 时， 相对径向分布函数gAB(r) . 图中标注的圆圈为第一个零根， 代表单种粒子的团簇尺寸. 由图10(b)可知， 随时间t增大， 团簇尺寸增大， 并于t=1×104开始达到最大值.

4 结 论

在二维周期边界条件下， 考虑时间延迟反馈作用的影响， 文章提出了一种手征活性粒子混合物的分离方法. 分别研究了角速度ω、反馈强度Kfb、反馈时间τ、转动扩散系数Dθ、自驱动速度v0及填充率φ对粒子有效扩散系数D和分离系数S的影响.手征活性混合粒子体系在没有驱动源时并不包含自分离属性， 但存在时间延迟反馈时， 系统的原有状态参量与反馈相耦合， 形成对混合粒子系统的驱动. 由于两种粒子在不同参数空间中对驱动的响应存在差异， 当ω，Dθ，v0及φ取最优值， 1)Kfb＞6.0 ，τ ＞1.0时， 时间延迟反馈使得CCW 粒子加快旋转角速度， 而对CW 粒子几乎无影响， CCW 粒子扩散完全由粒子之间相互作用控制， CW 粒子扩散由自身参数和相互作用力大小共同决定，S＞0.8 ，粒子分离. 2) 当Kfb＜6.0 ，τ＜1.0 时， 时间延迟反馈对两种粒子角速度调制差异较小， 两种粒子扩散不仅与粒子之间相互作用有关， 也与自身参数(角速度、自驱动速度及转动扩散系数)有关，S较小，粒子混合. 所以， 粒子是否实现分离是由两种粒子扩散的控制因素决定. 可以通过调节时间延迟反馈的强度和反馈时间来控制CCW 粒子扩散受到CW 粒子扩散的影响程度， 继而实现粒子分离. 研究结果在许多微生物中有潜在应用， 如旋转外场中的磁定向细菌， 固体边界附近的细菌及做涡旋运动的精子细胞等.

感谢华南师范大学艾保全教授对本文的指导.