关于空气质量监测数据的探索性分析

段 峰，王 杰

（1.铜陵职业技术学院基础部，安徽铜陵244061；2.安庆师范大学经济与管理学院，安徽安庆246133）

空气污染对生态环境和人类健康危害巨大，随着国家环保战略的提出，治理空气污染被提到了空前的高度。通过对“两尘四气”（PM2.5、PM10、CO、NO2、SO2、O3）浓度的实时监测，可以及时掌握空气质量，对污染源采取相应措施。“两尘四气”浓度的实时监测主要有两种方式，一是国家控制站监测，二是社会机构应用微型空气质量监测仪进行监测[1]。

虽然国家监测控制站点（国控点）对“两尘四气”有监测数据，且较为准确，但因为国控点的布控较少，数据发布时间滞后且花费较大，无法给出实时快速的空气质量监测结果和预报。国内许多公司积极响应国家环保战略，自主研发了各种微型空气质量监测仪。这种空气质量监测仪造价相对较低，可对某一地区空气质量进行实时网格化监控，并同时监测风速、压强、降水量、温度、湿度等气象参数。这些监测仪所使用的电化学气体传感器在长时间使用后会产生一定的零点漂移和量程漂移[2]，非常规气态污染物浓度变化对传感器存在交叉干扰，以及天气因素对传感器的影响，它们都造成微型空气质量监测仪所采集的数据与该地同一时间国控点采集的数据存在一定的差异。下面通过探索性数据分析方法来寻找数据的差异以及产生差异的主要原因。

探索性数据分析[3]（EDA）是指对观察或调查所得到的原始数据，在尽量少的先验假设下通过作图、制表、方程拟合和计算特征量等手段探索数据的结构和规律的一种数据分析方法，该方法在20世纪70年代由美国统计学家J.K.Tukey提出。与传统的数理统计分析方法相比较，EDA是一种更加贴合实际情况的分析方法，它强调让数据自身“说话”，发现蕴含在数据中的深层信息。从20 世纪80 年代开始，EDA 技术和方法被逐渐应用到各个领域。

1 数据来源

以2019 年全国大学生数学建模竞赛D 题[4]《空气质量数据的校准》附件1 和附件2 的数据为基础。附件1给出了从2018年11月14日至2019年6月11日共4 200组整点时刻的“两尘四气”数据；附件2给出了相同时间段内分钟时刻的“两尘四气”数据和5个天气因素（风速、压强、降水量、温度、湿度）数据。本文将国控点和自建点相同时刻的监测数据提取出来如表1所示，这是最能体现国控点和自建点监测误差的数据。

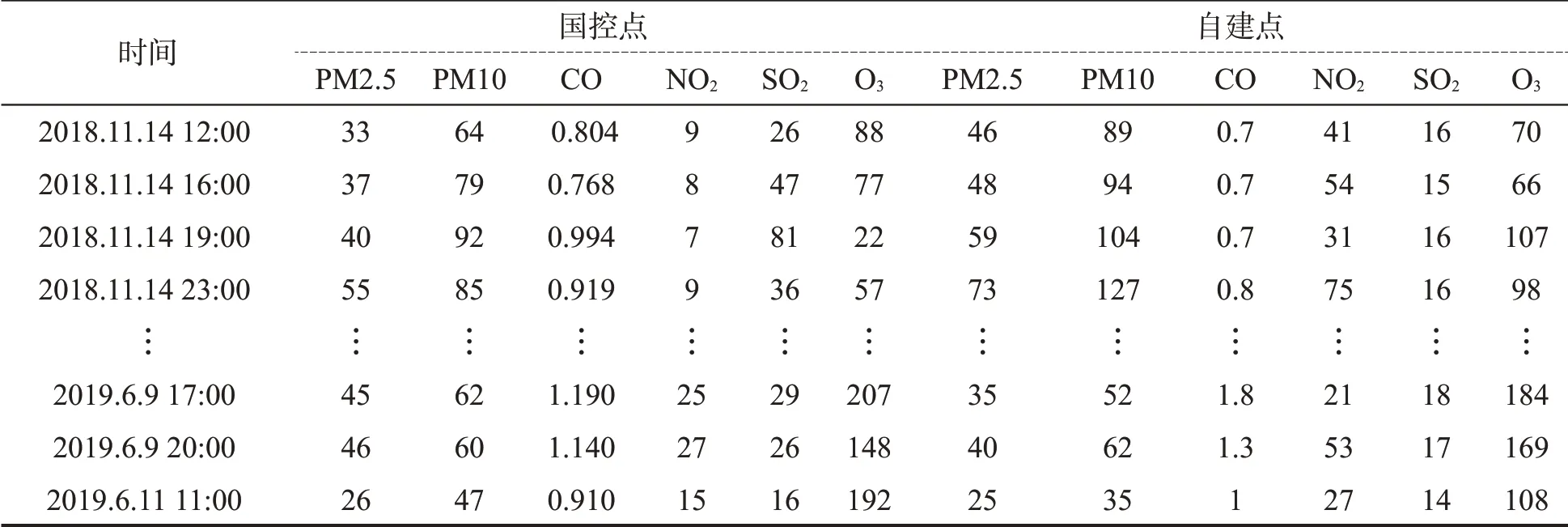
表1 相同时刻国控点与自建点“两尘四气”监测数据对照表

2 空气监测仪的差异性的EDA

2.1 数字特征分析

利用Excel对国控点数据和自建点数据分别求均值和标准差，结果如表2所示。

表2 相同时刻“两尘四气”监测数据的均值与标准差表

从均值看，国控点和自建点监测数据在均值方面差异显著，PM2.5、PM10、NO2和O3这4种污染物的国控点均值显著小于自建点均值；CO和SO2两种污染物的国控点均值显著大于自建点均值。从波动看，除CO和O3两种污染物的国控点波动比自建点波动大外，PM2.5、PM10、NO2和SO2这4种污染物的国控点波动都显著小于自建点的波动。这说明自建点的微型监测仪发生了显著的零点漂移和量程漂移。

2.2 图形趋势线分析

根据表1 数据，利用Matlab 软件[5]绘制“两尘四气”的国控点数据与自控点数据随时间变化的趋势图，见图1。

图1 国控点数据与自控点数据随时间变化的趋势图

图1传达出的信息非常粗略，可描述为：国控点监测数据与自控点监测数据差异显著，出现了明显的奇异点（图中针状点对应的数据）。但认真比对表1数据发现，PM10数据中明显的奇异点是国控点数据导致，具体出现在2019年2月19日14时，国控点PM10数据突然变大到985，而其前后整点时间数据为27和29，同时刻自建点数据为81。自建点SO2数据和O3数据一般变化不大，但一旦变化起来，数值差异太大，例如2019年1月23日一天自建点的SO2数据和O3数据忽高忽低，变化很大，而当天的国控点数据却比较稳定，这说明自建点的微型监测仪发生了比较严重的零点漂移和量程漂移，具体数据见表3。

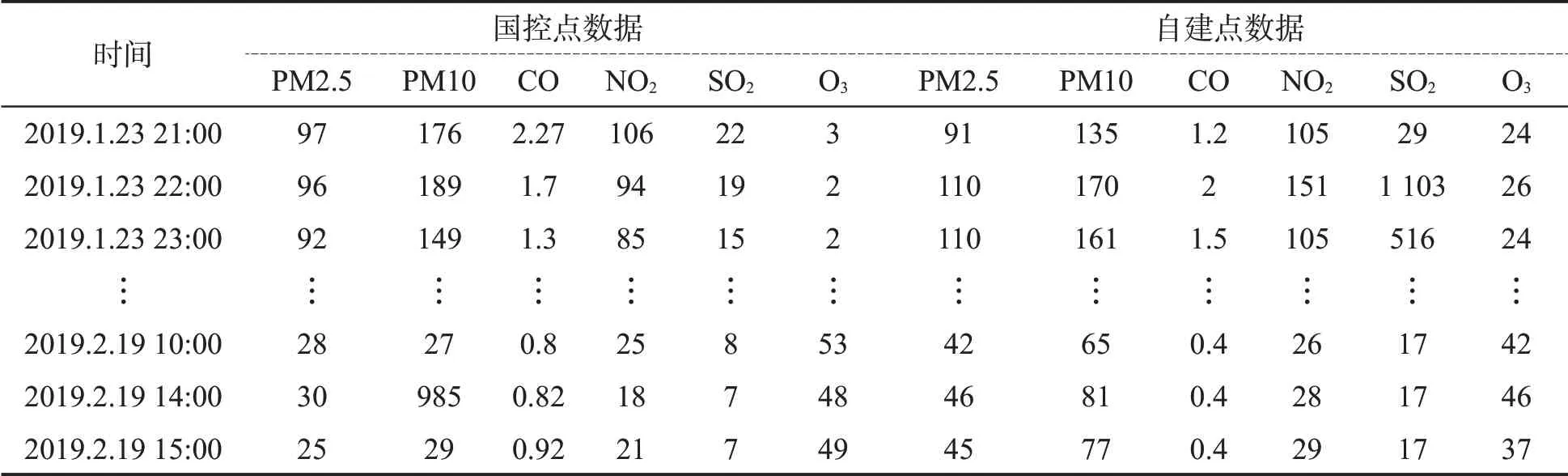
表3 国控点与自建点同时刻点对应奇异数据

通过图1还可以发现，数据变化及振荡趋势有非常粗略的一致性，不能看出时间因素对两组数据差异的影响，也就是数据差异与时间因素没有显著的关系。

2.3 图形直方图分析

将表1数据等距分割为100个区间，统计各区间上出现的数据个数，并转化为频率，然后用Matlab的histogram函数[6]绘制直方图，见图2。

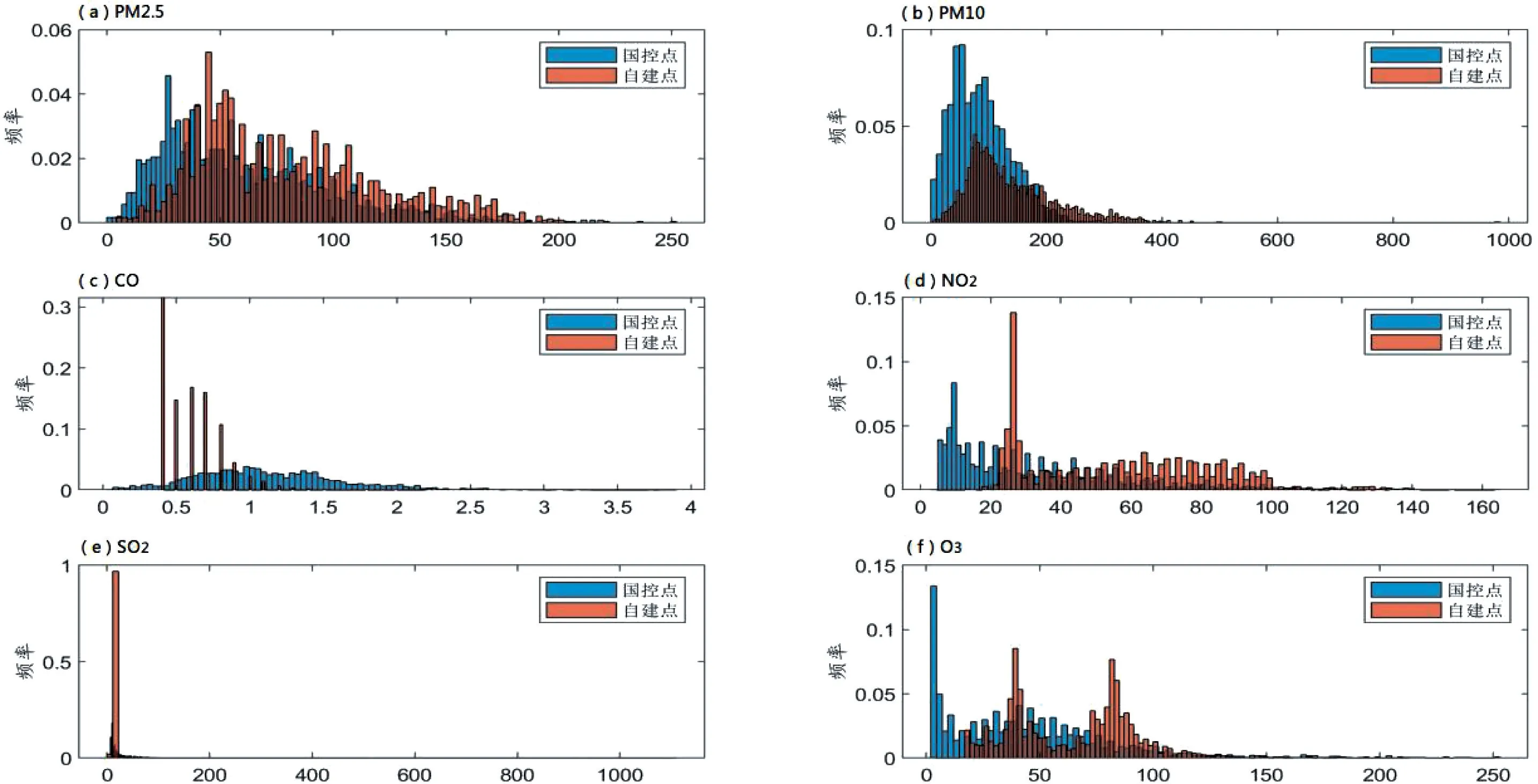
图2 国控点数据与自控点数据直方图

图2 表明两组数据有更加明显的差异：同一个区间，自控点数据相对国控点数据整体上差异很大，其中PM2.5、PM10、NO2和O3的国控点数据显著小于自建点数据，CO 和SO2国控点数据却大于自建点数据，这与表2给出的两组数据均值结果完全吻合。

2.4 图形误差分析

自建点数据与国控点数据之差就是自建点误差，用Matlab做出“两尘四气”随时间变化的误差图，如图3所示。

图3 国控点与自控点数据误差随时间变化图

在CO的误差图中，可以发现自建点数据都有一致小于国控点数据的趋势，其他污染物这一现象不明显。另外，所有污染物误差图中误差线都包括“0”在内，说明尽管误差存在，但两组数据基本上都在同一个水平上，自建点数据的误差是可以进行有效校正的。最后，通过误差图可以看到，时间因素对误差没有明显的影响。

以上从数字特征和图形特征两方面揭示了国控点监测数据与自建点监测数据的特征，通过不同的视角分析二者存在明显差异。那么，差异性存在的原因是什么呢？从赛题给出的数据，不妨尝试寻找自建点数据与国控点数据绝对误差与附件2所提供的五个天气因素（风速、压强、降水量、温度、湿度）之间的关系。

3 5个天气因素与测量误差的关联性的EDA

在自建点、国控点同时刻点数据中，对“两尘四气”数据求绝对误差，并提取同时刻点自建点数据中的5个天气因素数据，建立绝对误差数据与气象参数数据的关系表，见表4。

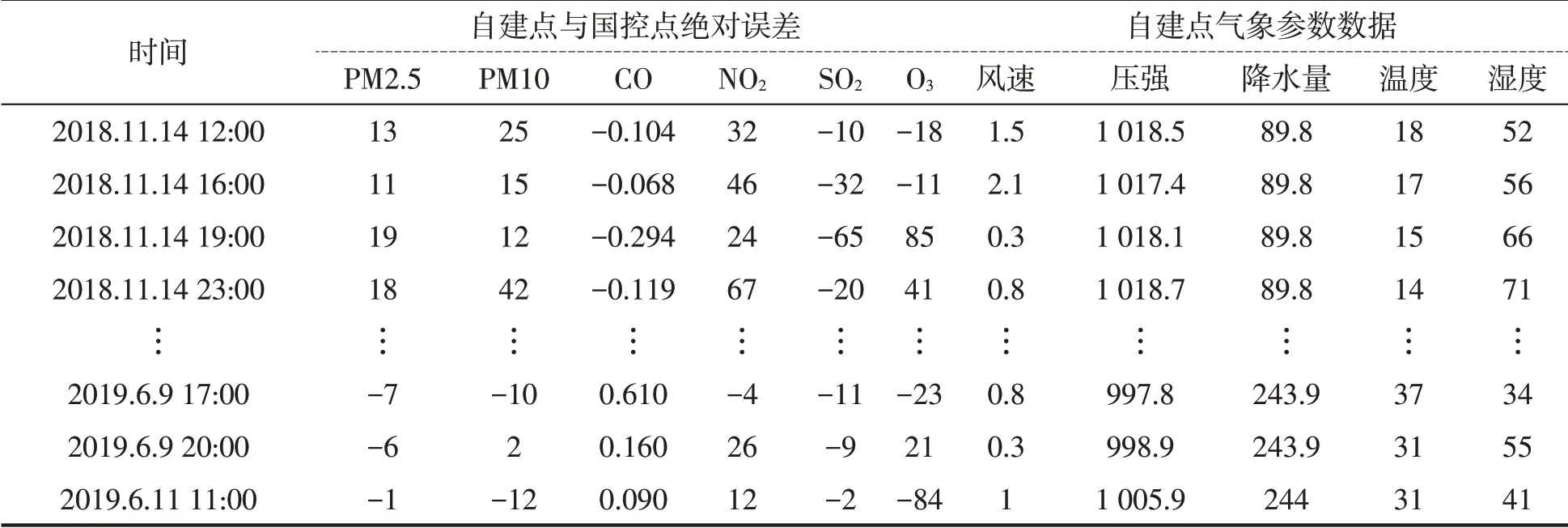
表4 自建点与国控点对应时刻绝对误差与自建点气象参数数据

由于污染物数据的绝对误差受到天气因素的影响，影响因子比较多，故采用灰色关联度分析法。灰色关联度分析法[7]是根据因素之间发展趋势的相似或相异程度，作为衡量因素间关联程度的一种方法。它利用数据序列曲线的贴近度来判断各因素之间的关联度。一般情况下，曲线之间越贴近，相应序列之间的关联度就越大，反之就越小。下面分4个步骤进行。

第一步：选取空气污染物PM2.5、PM10、CO、NO2、SO2、O3的浓度绝对误差数列为参考数列，5个天气因素风速、压强、降水量、温度、湿度数列为比较数列，其中参考数列记为x0(i)，比较数列记为xj(i)。第二步：对参考数列和比较数列进行无量纲化处理。不妨采用极差法，令

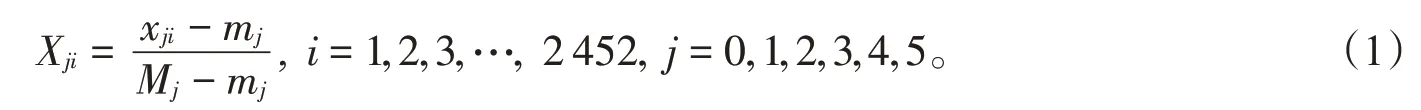
第三步：计算关联度系数

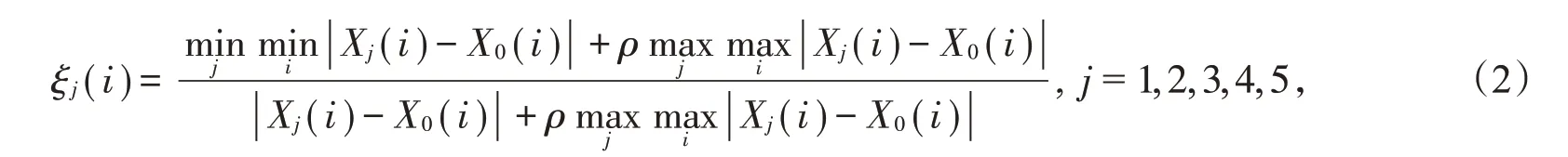
将表4 国控点与自建点对应时刻绝对误差与自建点气象参数数据代入式（1）（2），取ρ=0.5，利用Matlab 编程计算，可得各空气污染物PM2.5、PM10、CO、NO2、SO2、O3浓度误差与各气象参数的关联系数，部分结果见表5。

表5 空气污染物浓度误差与各气象参数的关联系数表

第四步：计算关联度。按照关联度公式

将表5 中的关联系数代入式（3），可计算出空气污染物PM2.5、PM10、CO、NO2、SO2、O3浓度的相对误差与5个气象因素的关联度。显然，关联度越大，气象因素影响就越大。计算结果如表6所示。

表6 各污染物浓度误差与各气象因素的关联度

由表6可知，压强和风速是导致污染物浓度误差的重点气象因素，（1）导致PM2.5浓度误差的气象因素由强到弱排序依次为：压强，风速，温度，湿度，降水量；（2）导致PM10浓度误差的气象因素由强到弱排序依次为：压强，风速，温度，湿度，降水量；（3）导致CO浓度误差的气象因素由强到弱排序依次为：压强，风速，湿度，温度，降水量；（4）导致NO2浓度误差的气象因素由强到弱排序依次为：压强，风速，温度，湿度，降水量；（5）导致SO2浓度误差的气象因素由强到弱排序依次为：压强，风速，降水量，温度，湿度；（6）导致O3浓度误差的气象因素由强到弱排序依次为：风速，压强，降水量，温度，湿度。

4 结束语

综上所述，EDA明确了国控点、自建点数据的差异性是显著的、可视化的。尽管自建点监测数据存在较大的误差，但自建点数据与国控点数据基本上都在同一个水平，可以对自建点数据进行校准、修正[8]。造成数据差异与自建点微型监测仪发生的零点漂移和量程漂移和5个天气因素有关，而与时间因素关系不明显。

通过关联度分析，文中给出了6个污染物监测数据误差与5个气象因素之间的关联度数据，给出了5个气象因素对自建点监测误差影响的强弱排序，这些数据和结果是进行误差校准的重要依据，为数据校准提供了充分的条件。因此，以5个天气因素为自变量，建立数学模型来校准数据就顺理成章了。