稀疏数据情况下小椭圆轨道目标再入预报方法

张炜，崔文，张育卫，刘兴，李菊清

(西安卫星测控中心，西安710600)

1 引言

大气阻力是即将再入空间目标所受的最主要非保守摄动力，精确的空间目标面质比及合理的大气阻力特性建模是准确计算大气阻力加速度、预报再入时间的关键。大气阻力系数与空间目标外形、表面材料、大气组成及温度等密切相关，同一个目标的大气阻力系数在不同轨道高度、不同太阳活动水平等情况下会有较大差异[1]。通常，空间目标的准确外形、质量、姿态和表面材料等都是未知的，分别确定大气阻力系数、迎风面积和质量难度很大，因此引入弹道系数B进行统一处理[2]。弹道系数的定义为:

式中，CD为大气阻力系数；A为迎风面积；m为质量。

在大气阻力的影响下，空间目标的轨道不断衰减，轨道形状越来越圆，最终坠入稠密大气层。按初始远地点高度Ha_ini(本文的 “初始”指空间目标再入前10天)对再入目标轨道进行分类:

(1)近圆轨道:Ha_ini＜500km

(2)小椭圆轨道:500km≤Ha_ini＜5000km

(3)大椭圆轨道:Ha_ini≥5000km

依此统计，2012—2018年非受控再入的大型空间目标数量，结果如图1所示。可以看出，每年再入的大型空间目标中小椭圆轨道目标不在少数，近7年平均占1/6以上，2018年更是超过40%。

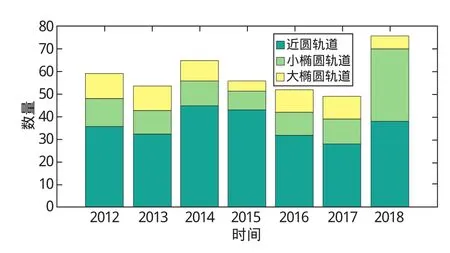
图1 2012年至2018年非受控再入的大型空间目标数量Fig.1 Number of large uncontrolled reentry objects from 2012 to 2018

再入预报的主要难点在于轨道确定和大气阻力建模[3]，一般在足够测量数据的基础上确定精确轨道并解算弹道系数，但是只有少数国家和组织具有获取再入目标测量数据的能力。即使可以，相邻圈次的间隔可能太长导致难以联合使用确定精密轨道，容易出现定轨残差太大、不收敛等问题，这也是本文 “稀疏数据”这一基本背景。“地球重力场和海洋环流探测卫星”(GOCE)再入前20天起，布设于德国Wachtberg的跟踪及成像雷达 (TIRA)共获取12圈次测量数据，不同数据组合的定轨结果明显差异[4]，在没有基准星历的情况下难以选优。目前大部分再入预报研究只能依靠美国战略司令部于Space-track网站公开发布的两行根数 (TLE)，基于TLE的再入预报方法研究主要聚焦于TLE的预处理[5，6]，或利用TLE解算弹道系数、太阳光压系数、状态矢量等[7-11]。几乎所有的研究均假设再入目标的弹道系数是一个常数，显然这是不够准确的，尤其对于椭圆轨道再入目标而言，容易忽略弹道系数变化带来的问题。

相较于近圆轨道目标，小椭圆轨道目标的再入预报难度更大。主要原因是小椭圆轨道目标再入过程中几乎每圈都要穿过整个稠密大气层，高度变化导致同一轨道周期内弹道系数变化明显。实际应用中发现，若采用整个数据弧段内解算单个弹道系数的策略，各测量元素的残差可能较大，难以判断轨道确定结果的准确性，而采用分段解算多个弹道系数的策略，虽然可以获得更加精确的目标轨道，但是进行再入预报时弹道系数的初值难以选择。

本文针对稀疏数据情况和小椭圆轨道的特点，提出使用平均弹道系数进行再入预报。利用半数值法计算平均弹道系数、数值法进行短弧数据轨道确定和轨道外推，并使用实测数据进行效果验证。结果表明，本文提出的方法可有效避免稀疏数据情况下小椭圆轨道目标轨道确定收敛难或残差过大、再入预报时弹道系数难确定等问题，预报精度达到与近圆轨道目标同等水平。

2 方法

本文针对稀疏数据情况和小椭圆轨道的特点，提出半数值法和数值法相结合预报再入时刻。 使用经典轨道根数σ(a，e，i，Ω，ω，M) 描述再入目标轨道， (a，e，i，Ω，ω，M) 分别为半长轴、 偏心率、倾角、升交点赤经和平近点角。

2.1 轨道确定

稀疏数据情况是指测量数据圈次太少，例如24h内仅有1～2圈测量数据，多圈数据联合确定轨道时容易出现残差太大、不收敛等问题。本文使用短弧数据定轨方法对单圈数据分别确定轨道，考虑的摄动项包括:地球非球形引力、大气阻力和日月引力。短弧数据定轨的问题主要在于轨道外推时误差容易迅速发散，但是本文仅需数据弧段内的6个参数，可有效避免不收敛和误差发散等问题。轨道结果精度主要受限于测量精度，与基于大量测量数据的精密轨道相比，短弧数据轨道位置误差一般为几百米，且主要集中在对再入预报影响最小的沿迹方向[12]。

基于单圈测量数据的轨道确定结果为密切根数 (σ1，σ2，…，σN) ， 本文还用到对应的平根数。去除密切根数中的短周期项即可得到平根数，即:

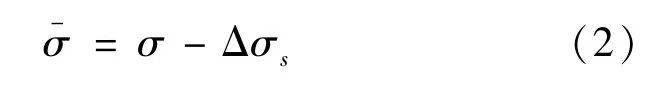
式中，为平根数；σ为密切根数；Δσs为短周期项。平根数的计算方法及短周期项的详细讨论可参考文献 [13]—文献 [16]。没有可用测量数据的情况下可以使用TLE根数作为伪测量数据，使用SGP4/SDP4模型解析TLE历元时刻的位置速度，并转换成轨道根数。

2.2 平均弹道系数

如何计算再入目标的弹道系数是许多再入预报研究的焦点。在大多数研究中再入目标的弹道系数被视为常数，采用将弹道系数作为待估参数的策略，在轨道确定时与状态参量(r，r)一同求解，再基于弹道系数和状态参量的解算结果进行再入预报。但是这种方法对小椭圆轨道目标并不完全适用，由于空间目标的弹道系数 (主要是大气阻力系数)随高度变化，如果整个数据弧段内解算单个弹道系数，各测量元素的残差可能较大导致难以判断轨道确定结果的准确性；如果分段解算多个弹道系数，进行再入预报时难以选择弹道系数的初值。为避免这些问题，提出基于空间目标轨道周期内的弹道系数平均值进行再入预报。平均弹道系数反映了一轨道周期内大气阻力的平均效果，定义为:

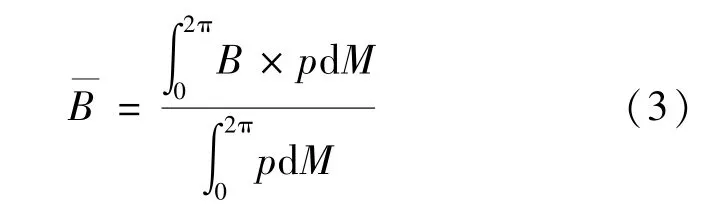
式中，ρ为大气密度值。为书写方便，下文统一写为B。

大气阻力仅有长期作用效果，因此进行弹道系数拟合时可以采用开普勒平根数作为根数系统，并使用半数值法进行轨道积分，积分考虑的摄动项包括地球非球形J2项、J3项、大气阻力。使用半数值法时高阶摄动力建模较为困难和复杂，且精度改进效果不明显[17]。积分模型如下[18]:

式中，v为再入目标相对大气的运动速度；f为真近点角；ωE为地球运动速率；μ为地球引力常数；rE为地球半径；n为平运动；p为轨道半通径；J2、J3分别为地球引力场二阶、三阶带谐系数。本文使用MSIS-90模型计算大气密度。由于根数系统不包含短周期项，因此积分步长可以使用轨道周期的整数倍。

假设已有空间目标连续N组轨道平根数(，)，平均弹道系数的计算过程如下:

(1)以及初始平均弹道系数B0为初值，一轨道周期为步长对公式 (4)进行反向积分。反向积分的目的是防止弹道系数初值偏差太大导致积分过程 “钻地”。

(2)若积分时刻与历元之差小于半周期，则计算当前时间半长轴计算值与实测值之差Δak及半长轴对弹道系数的偏导数根据公式 (5)计算:

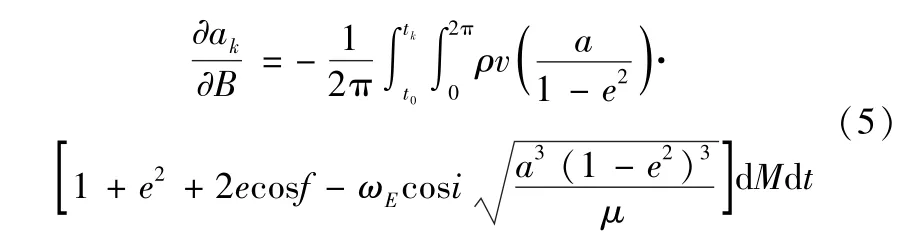
(3)第1条根数计算结束后，使用公式 (6)计算弹道系数修正值:

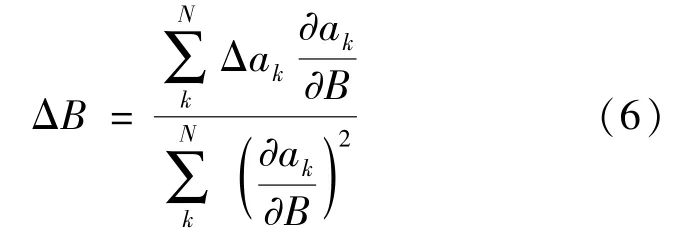
(4)若ΔB小于收敛阈值，则计算结束，否则对弹道系数进行修正:Bj+1=Bj+ΔB，返回 (1)重新计算。

2.3 再入时间预报

以第N圈数据确定的轨道密切根数σN及弹道系数计算结果B为初值，用数值积分的方法进行轨道外推，直到再入目标的平均轨道高度低于80km，积分结束时间后约5min即为空间目标的再入时间。数值积分使用10阶定步长KSG积分器，用到的摄动力及其模型如表1所示。

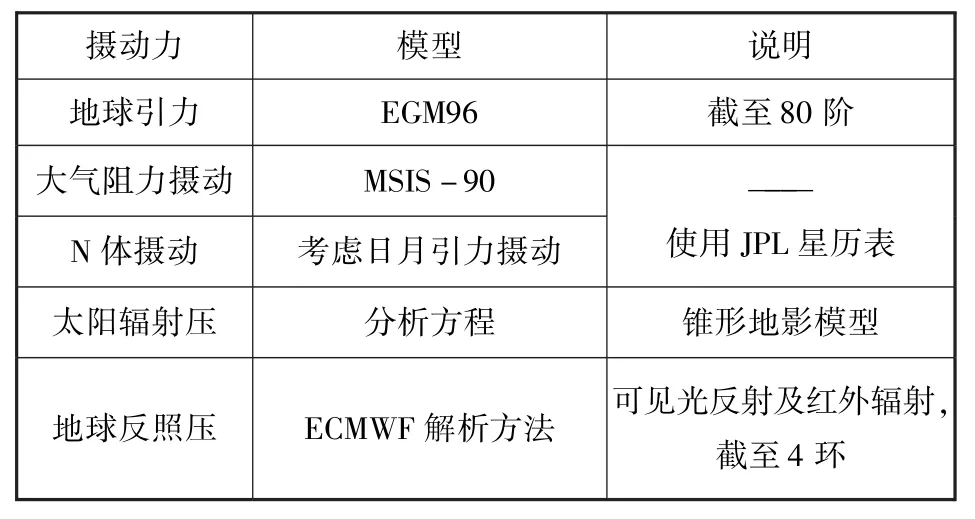
表1 再入预报使用的摄动力及模型Table 1 Dynamical and geometrical models employed in the reentry prediction

由于不同大气模型计算得到的大气密度值存在差异[19]，因此弹道系数拟合和再入预报时应使用同一大气模型，本文均使用MSIS-90模型。

3 数据与结果

使用误差百分比δ评估再入预报的精度，误差百分比δ用下式计算:

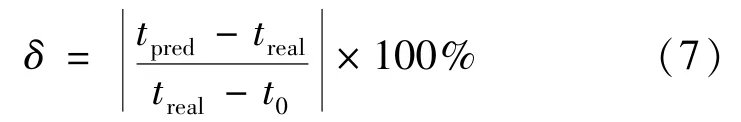
式中，treal为空间目标的实际再入时间；tpred为预报的再入时间；t0为进行再入预报所用初轨的历元。从公开资料看，近圆轨道空间目标的再入预报误差基本在10%～20%之间，部分预报结果误差甚至可能超过30%，这主要取决于再入过程中再入目标姿态和大气环境的变化[20，21]。

选择美国铱星52(NORAD编号为25169)作为算例目标进行验证，其初始近地点高度约为154km、远地点高度约为608km。根据Space-track网站发布的信息，铱星52的再入时间为2018-11-05 21∶20(UTC)，与本文最后一次预报结果基本一致，因此treal取为 2018-11-05 21∶20(UTC)。从2018年10月27日起，选择间隔10h以上的连续3圈测量数据进行再入预报，铱星52的平均弹道系数及再入时间预报结果如表2、图2所示。

为了更直观地理解平均弹道系数的计算效果，预报时大气环境参数使用的均为实际观测值，期间大气环境平静，大气模型误差对平均弹道系数结果影响较小。从计算结果看，铱星52的弹道系数在0.0251～0.0256m2/kg之间变化，均值为0.02548m2/kg，上下浮动1%左右，远小于大气阻力系数轨道周期内约10%的变化幅度，验证了平均弹道系数计算方法的准确性和有效性。10次再入时间预报结果中的最大误差仅为3.25%，其中8次计算的误差小于1%。

按照本文提出的再入预报方法，选择TLE作为数据源对2017年再入的11个小椭圆轨道目标进行再入预报。再入预报时将5天内每天1组TLE组成根数序列，并将根数序列视为再入目标的实测轨道值。再入前10天起每天进行一次预报，预报时大气环境参数使用预报值，具有不确定性，各目标10次预报中的实际最大预报误差如图3所示。可以看出，11个目标中9个目标的再入预报误差小于15%，预报误差与初始偏心率 (或初始远地点高度)无明显相关性，说明本文方法具有较好的适用性。另外两个分别为35.6% (目标NORAD编号为41726)和42.5%(目标NORAD编号为09980)，由于TLE使用前未作异常值筛选，分析认为异常TLE是造成这两个目标最大误差偏大的主要原因。从图3也可以看到，使用TLE进行再入预报也能获得较高的预报精度。

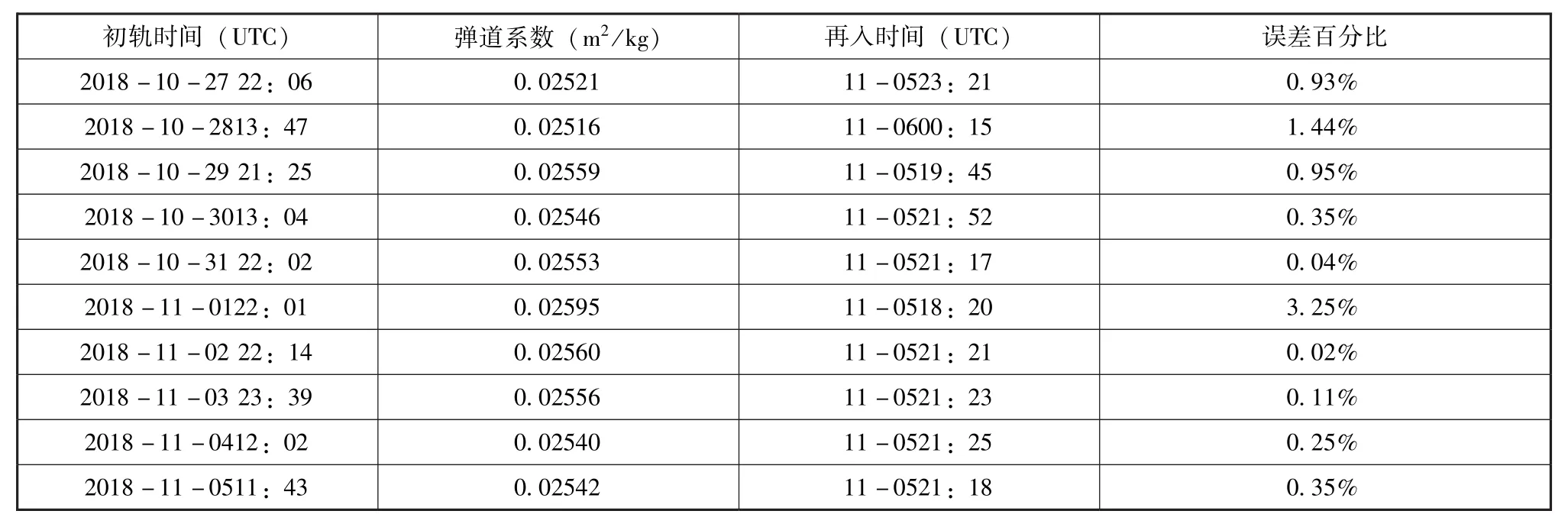
表2 铱星52再入预报结果Table 2 Reentry prediction results of Iridium-52

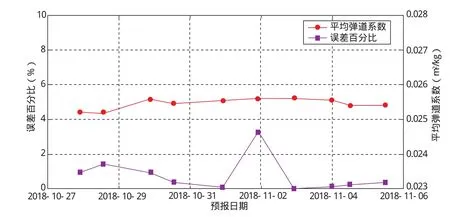
图2 铱星52的再入预报误差百分比及弹道系数Fig.2 Relative error and mean ballistic coefficient of Iridium-52

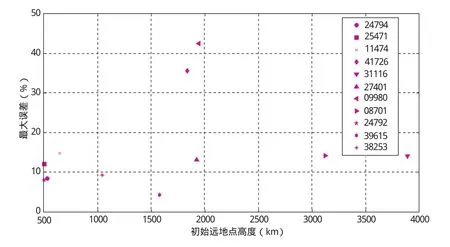
图3 2017年再入的11个小椭圆轨道目标的最大预报误差Fig.3 Maximum relative error of 11 reentry objects with low-eccentricity orbits in 2017

4 结论

由于大气阻力系数随高度变化，小椭圆轨道目标的再入预报比近圆轨道目标难度更大。本文针对稀疏数据情况和小椭圆轨道的特点，提出使用平均弹道系数进行再入预报，并使用再入目标的实测数据进行验证。结果表明，基于平均弹道系数进行小椭圆轨道目标再入预报，可有效降低再入预报误差，预报精度达到与近圆轨道目标同等水平。