陨石音爆研究思路及弹道靶试验

王宗浩，党雷宁，柳森

(中国空气动力研究与发展中心超高速所，绵阳621000)

1 引言

小行星极高速进入稠密大气过程中会产生较大范围的冲击波，可能造成地面建筑物损毁和人员伤亡。冲击波产生的原因有两种，一是陨石在空中爆炸，二是陨石极高速飞行产生的强激波，即音爆。陨石音爆的形成机理与超声速飞机类似，都是激波穿过大气传播到地面造成局部短时超压，不同的是陨石飞行马赫数极高，形成的激波形状类似圆柱形，且激波强度更大。

人们认识音爆问题始于第二次世界大战末期对超音速射弹飞行产生的激波的研究，但直到1947年美国X-1飞机超越音速，音爆才开始引起学者的广泛关注。经过数十年的试验和理论研究，目前从现象和规律层面对音爆都已经有比较全面的掌握，包括在非均匀大气中的传播、飞机非定常飞行时的效应等。但针对陨石在大气层内极高速 (通常为数千米/秒至数十千米/秒)飞行所导致的音爆现象，国内外研究报道较少。

本文总结了当前音爆研究的主要理论、计算方法和试验技术，从陨石音爆问题出发，分析了其中的科学问题和现有研究手段的不足，提出了一种仿真和试验结合的陨石音爆问题研究策略，并结合弹道靶试验开展了陨石音爆的初步测量和仿真对比。

2 音爆研究方法

2.1 经典音爆理论

考虑平面波扰动下的介质微元，由波动方程可得到扰动波的传播速度:

当扰动波为小振幅声波时，由于声压很低，声波的传播速度可近似为U∗≈c0，但是对于音爆这种有限振幅的波动，当地声速和振动速度均为不可忽略的非线性项，因此波形在传播过程中会产生畸变，如图1所示。图中，A点为正峰压，其传播速度快于c0，随时间推移逐渐超前到波的头部；B点为负峰压，其传播速度慢于c0，随时间推移逐渐落后到波的尾部；最终形成N形波。

经典的音爆传播模型，针对于亚声速和一般超声速均匀流动，采用小扰动假设将基本方程线性化 (但是对于跨声速和高超声速流动，基本方程简化后仍然是非线性的)，得到的表征扰动传播方向的特性线是一系列角度等于马赫角的平行线。而如前所述，实际超声速扰动波的传播速度是受到当地声压和扰动速度变化影响的，特征线存在相交，扰动相互叠加并形成激波。因此，直接采用线性简化方法并不能很好地描述音爆形成和传播机制。1952年，Whitham提出一个修正的小扰动线化理论[1]，确定了特征线叠加所形成的激波线位置，并给出了远场扰动速度计算式的形式:

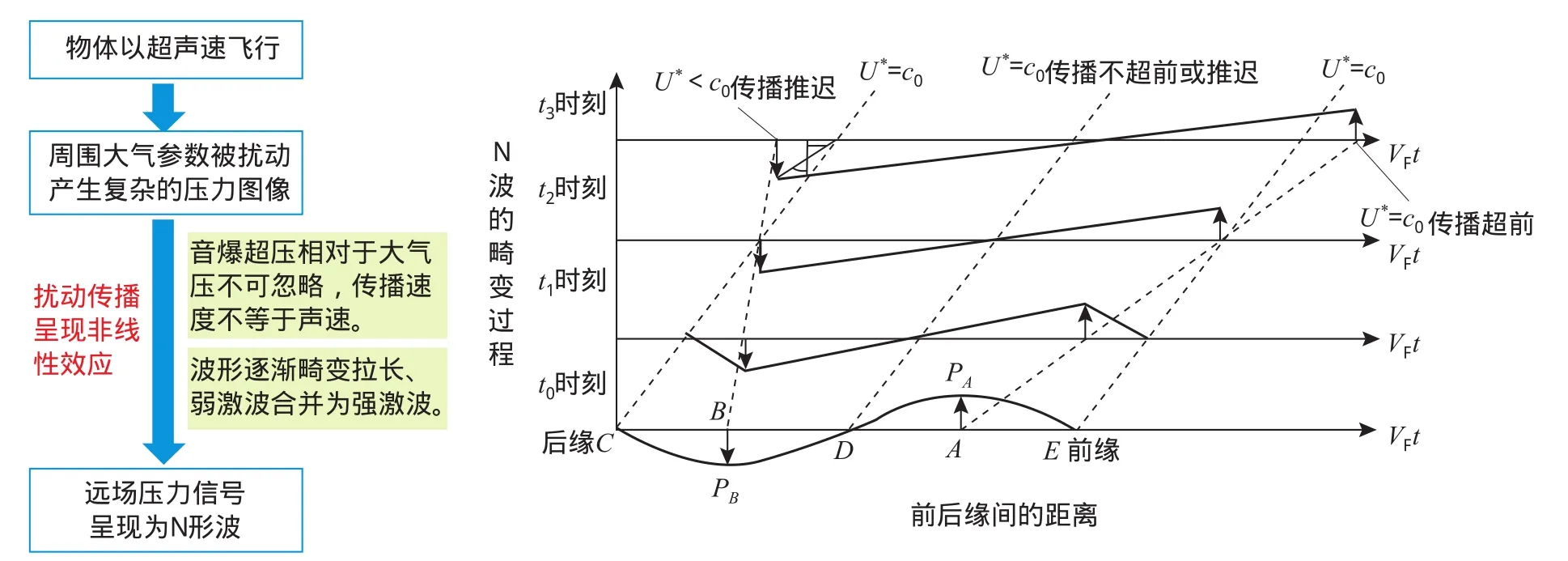
图1 平面行波声压波形的畸变过程Fig.1 Distortion process of sound pressure waveform of traveling plane wave

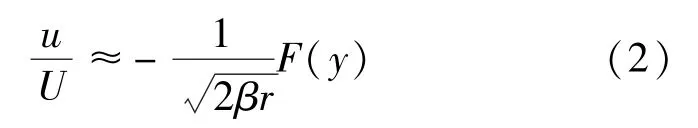
式中，F(y)为Whitham方程

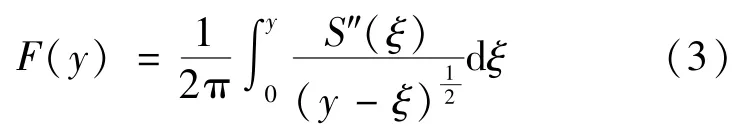
1963年，Friedman，Kane和Sigalla首先提出了基于射线跟踪法的音爆计算模型[2]，该模型可以更好地描述大气高度变化及层流风的影响，并且可以计算非定常飞行效应。但是Friedman等人的模型存在计算射线发展的侧向分量的错误。之后Hayes等人建立的ARAP模型解决了这一问题[3]。同一时期Thomas也研究了一套与Hayes相似的计算模型[4]，不同于Hayes采用估算一组封闭积分，Thomas通过对一组穿越大气层的射线路径进行数值拟合实现射线跟踪，并引入了 “波形参数”法实现了对传播过程的波形连续演化分析。波形参数法以其计算量小、精确度高的特点得到广泛应用。20世纪70年代，Carlson研究建立了一种简化音爆预测方法 (Simplified Sonic Boom Prediction，SSBP)，其以大量计算机计算结果为基础数据，并采用 “形状因子”表征不同类型的飞机，通过拟合求解音爆源强度[5]。

其它方面，试验测量表明大气风场和湍流对音爆的远场波形有明显影响，激波附近的波形会发生扭曲，峰值的上升时间会变长，采用射线理论求解连续波与湍流的相互作用非常困难。Crow通过在薄激波区域构建一种以与激波距离为参数的抛物面散射方程来描述激波的扭曲[6]。而对于上升时间的预测，Plotki和George研发了Burgers方程以描述与湍流有关的耗散问题[7]，Pierce研发了一种基于波前折叠的理论[8]，尽管这些方法并不完善，但至今仍然是仅有的可用于定量分析的模型。

2.2 现代音爆计算方法和相关程序

由于音爆研究空间尺度较大，当前主流的方法是将计算域划分为近中场和远场两个区域，如图2所示。近中场一般采用可压缩流动的CFD代码计算。远场计算以近中场CFD结果为输入条件外推到地表，其中涉及到压力波在分层大气的传输，风场和湍流、温湿度等的影响。远场的计算结果是评估音爆对地面人和建筑物影响的依据，是音爆数值计算的关键技术之一。

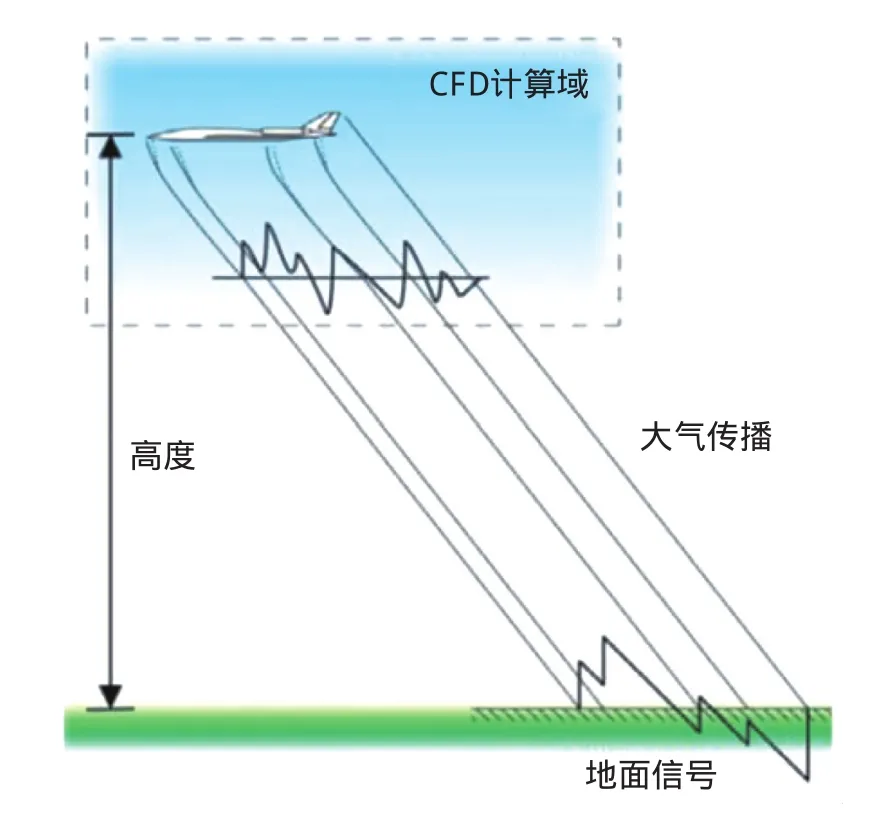
图2 音爆传播问题分区计算策略Fig.2 Zoning computation strategy for sonic boom

远场计算方法有多种，例如建立在几何声学基础上的F函数法和波形参数法、求解全速度势方程法、求解Burger方程法等，有的研究者甚至通过求解Euler方程来计算音爆的远场特性。

20世纪80年代以后，随着计算机技术的进步，CFD仿真逐渐取代了F函数求解近场源参数， 美国先后发展了 Cart3D[9，10]、 PCBoom[11]、sBoom[12]等多个音爆计算和优化软件，并通过多型飞机的实测数据对软件计算模型进行标定和验证。

2.3 音爆试验研究进展

音爆试验研究以飞行试验为主，美国自20世纪50年代起至今在超音速飞机研制需求推动下开展了系统性的试验研究工作。另外，以弹道靶为代表的特种超高速地面试验设备在音爆研究方面也发挥了独特作用。

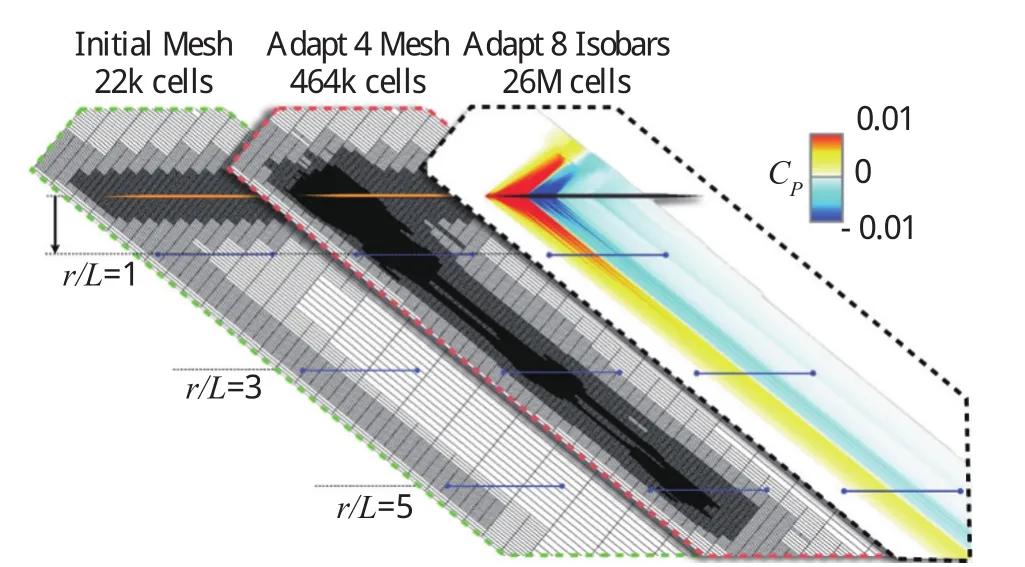
图3 Cart3D软件AXIE模型音爆计算网格优化结果Fig.3 Sonic boom computation grid optimization by Cart3D AXIE model

音爆的飞行试验采用地面布设的麦克风测量超音速飞机以不同高度、飞行参数和气候条件下掠过时的信号，通过对比分析理解和研究音爆的特性，校核和改进预测方法。1950—2000年，美国针对飞机音爆先后开展了10余项试验项目。早期的试验研究主要验证Whitham理论关于N形波幅值和长度与飞机几何尺寸间的关系。结果表明仅以飞机体积计算的飞机音爆最高可低于试验值40%，且随当地环境条件的变化，音爆从高空到地面的幅值会放大。这促进了机翼升力以及压力梯度对音爆影响的研究以及对音爆理论的修正。

美国国家航空航天局兰利研究中心 (NASALangley)从20世纪60年代开始探索音爆的风洞试验技术。受限于风洞尺寸，音爆试验的飞机模型需要缩比到很小，加工制造的难度极大。另外，非均匀和非稳态的风洞来流、模型和探针的振动、边界层效应以及近场压力信号的复杂性等都给风洞试验的设计和开展造成困难。尽管开展音爆地面试验模拟的难度很大，一些特殊的模拟设备，如弹道靶，依然可以在音爆问题试验研究中发挥作用。弹道靶采用火药或高压气体驱动的发射器加速模型到一定速度进入密闭的测试段自由飞行，由于没有支架和背景噪声干扰，试验结果可以为CFD方法验证提供很好的对比。

2000年，为验证一种新的低阻低音爆的钝前缘飞行器外形概念 (ABLE)，美国国家航空航天局-艾姆斯研究中心 (NASA-Ames)在弹道靶(HFFAF)上成功开展了自由飞模型的音爆测量试验[13]。选用的发射器口径为44mm，模型长度76.2mm，将压力传感器安装在测试段壁面，测量面与壁面平齐。图4为马赫数2，雷诺数3×106，对应模拟高度15km条件下测量得到的模型流场纹影图像和近场压力信号。

3 陨石音爆问题研究思路

3.1 陨石音爆研究中的科学问题

研究陨石音爆的重要意义在于准确预测其对地面的危害，为陨石事件的预警和防减灾提供指导，因此需要建立科学的方法预测给定弹道条件下的陨石音爆地面强度和影响范围。总体研究思路可以借鉴飞机音爆的研究方法，但其中面临的新问题需要关注。

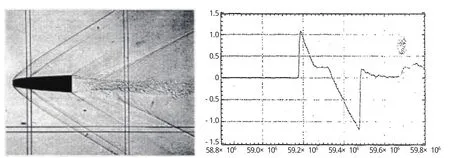
图4 HFFAF弹道靶自由飞模型的纹影图像和音爆波测量结果Fig.4 Schlieren image and sonic boom measuring result of HEFAF ballistic range free flight model

一是需要发展极高速条件下陨石近场流场和激波强度的计算模拟方法。陨石进入过程存在复杂的超高速空气动力学问题，如极高速进入条件下的气动力与轨迹、气动加热与烧蚀、高温气体效应等，而这些均属于当前空气动力学的难题。只有解决这些基础气动问题，建立相应的物理模型才可能较准确预测陨石近场激波结构和强度，从而获得陨石音爆地面影响分析的输入条件。

二是需要完善强激波大气传播理论。由于陨石飞行马赫数极高，其激波传播过程具有强非线性特征，基于小扰动假设的线性简化工程模型不再适用，需对现有方法和模型进行完善和验证。

三是获取真实试验数据面临挑战。针对飞机音爆的飞行试验研究容易实施，而陨石事件的稀少性和随机性给实地测量带来了困难。基于地面超高速试验设备发展陨石音爆测量技术开展地面模拟试验，可能是获取基础研究数据的唯一有效途径。

3.2 陨石音爆研究思路

结合当前理论基础和试验条件，采取计算与试验相结合的策略开展陨石音爆强度和传播规律研究是可行的。理论与计算方法方面，主要参考飞机音爆研究方法，将研究速度拓展到10km/s以上。试验方面，主要依托弹道靶设备开展2～7km/s速度范围的对比验证。

研究思路如图5所示。考虑高温烧蚀和真实气体效应条件下的化学反应，建立近、中场压力分布高精度数值计算模型，经弹道靶试验验证和改进后用于获得陨石飞行中的近、中场压力分布。以此为输入，进一步将结果外推至远场，需考虑大气密度梯度、风场和湍流、温湿度等的影响，可以尝试在现有方法，如求解Burgers方程等的基础上改进完善。

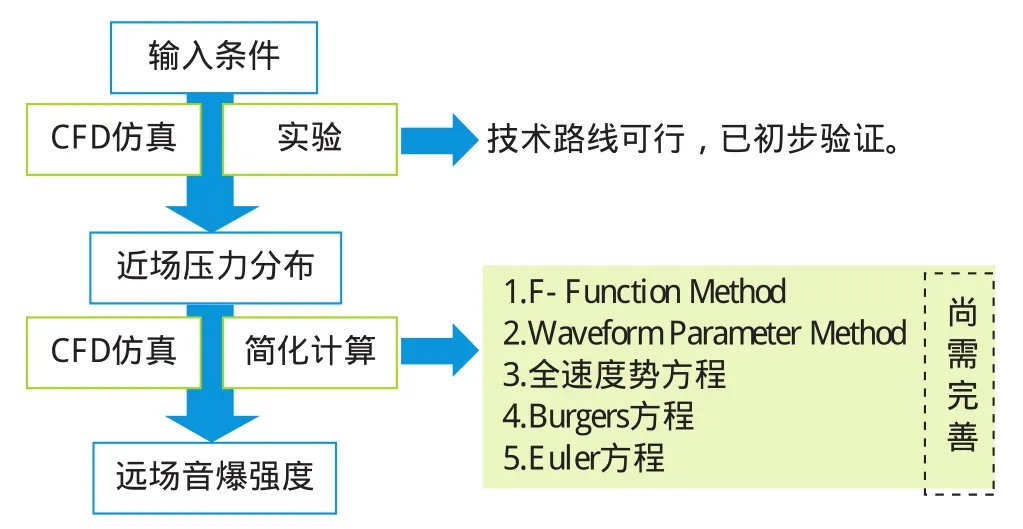
图5 陨石音爆研究方法Fig.5 Meteorite sonic boom research method

4 陨石音爆的弹道靶模拟试验

4.1 弹道靶陨石音爆试验方法

弹道靶是一种超高速模拟设备，其系统组成如图6所示。发射器系统采用二级轻气炮加速模型，最高速度可达8km/s；靶室系统为飞行测试段，可模拟大气环境；测试系统包含速度测量、流场显示、压力测量等仪器设备。

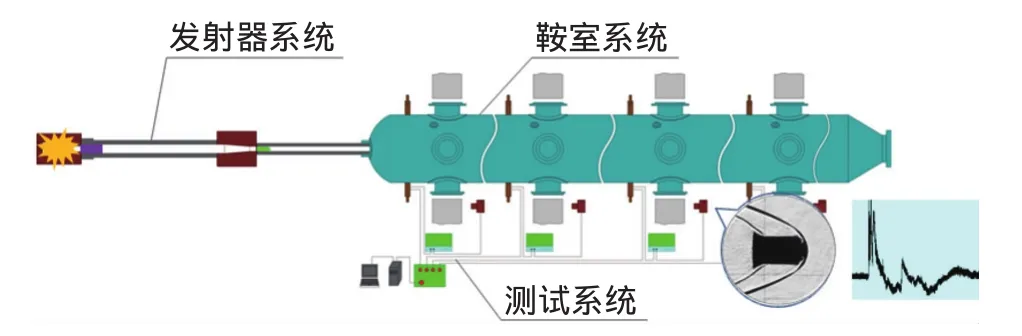
图6 弹道靶原理图Fig.6 Schematic diagram of ballistic range

采用弹道靶模拟陨石超高速飞行过程，可获得中、近场压力分布数据为计算方法研究提供校验数据。具体试验方法为:首先，设计适用于弹道靶设备的陨石模型，设计合理的压力测量方案，选择高精度的压力传感器搭建测量系统，如图7所示，布置高分辨率阴/纹影成像系统用于记录模型飞行姿态和流场结构；其次，在2～7km/s范围内选取典型状态开展试验测量，获得中、近场压力分布数据和流场显示结果；最后，用试验数据核验计算方法。

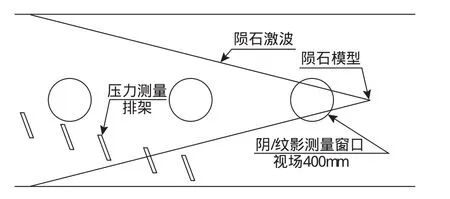
图7 弹道靶音爆测试布置示意Fig.7 Ballistic range sonic test layout

4.2 试验状态和结果

近期，为验证弹道靶开展陨石音爆研究的技术可行性，在中国空气动力研究与发展中心200m自由飞弹道靶上开展了一次测量试验，如图8所示。不同的陨石在材料成分、孔隙率、形状和尺寸等方面均存在差异，其中材料和孔隙率极大影响气动烧蚀乃至解体的程度，而流场结构和音爆强度主要决定于形状、尺寸和进入速度等因素。考虑到陨石一般为椭球形，结合弹道靶设备发射能力和模型飞行稳定性要求，选择长径比较小的球头柱加尾裙的旋成体为试验对象，其球头半径为30mm，总长度为50mm。虽然真实陨石表面的坑洞或孔隙会导致复杂的近壁面流场，简单模型无法完全模拟，但决定峰值超压的脱体激波强度与采用简化模型的结果是相近的，用于验证测量技术和计算方法是有意义的。试验中，模型飞行速度约3.5km/s，测试段为常压环境，在模型飞行轴线正下方112cm处前后间隔10cm布置了两支PCB113B28传感器 (采样频率500kHz)，模型尺寸及传感器布置如图9所示。

弹道靶陨石音爆测量试验获得的PCB传感器时域信号如图10所示，其中第一个N形波为陨石模型飞行激波首次扫掠测量面时的超压信号，其峰值超压约35kPa。

4.3 CFD计算对比

进一步，针对试验条件采用二维轴对称网格、理想气体和K-ω SST湍流模型开展了流场仿真，得到了模型近场不同距离处的音爆波形及峰值超压。结果显示模型近场由中心向外的激波超压呈快速衰减趋势，计算得到的音爆波形与试验测量结果相似，但峰值超压高于实测结果。要进一步提高计算方法的预测精度，则材料的气动加热和烧蚀损伤、真实气体的化学非平衡流动效应不可忽略。

图8 200m自由飞弹道靶Fig.8 200m free flight ballistic range

图9 弹道靶陨石音爆测量传感器现场布置情况Fig.9 Ballistic range meteorite sonic boom measurement sensor site layout

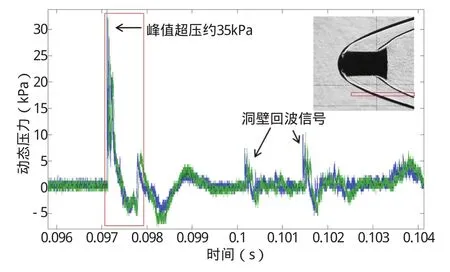
图10 弹道靶陨石音爆测量试验获得的PCB传感器时域信号和流场阴影图像Fig.10 PCB sensor time domain signal and flow field shadow resulting from ballistic range meteorite sonic boom measurement test

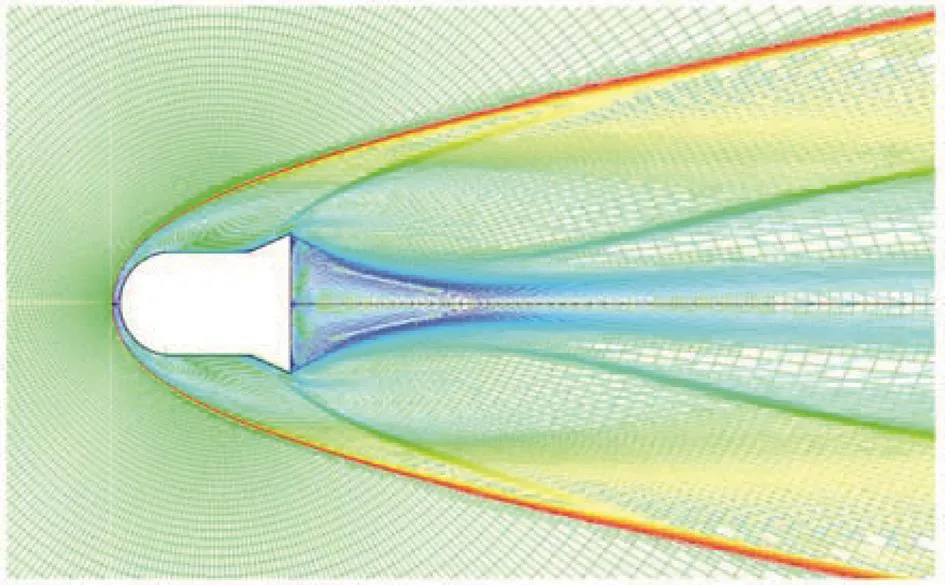
图11 CFD计算网格和流场马赫数云图Fig.11 CFD computational grid and flow field Mach number cloud image

5 结论

本文梳理了国内外在音爆预测理论、音爆试验模拟方法等方面的研究进展，从陨石音爆问题出发，分析了其中的科学问题和现有研究手段的不足，提出了一种仿真和试验结合的陨石音爆问题研究策略，并介绍了在弹道靶上开展陨石音爆模拟试验的方法和初步测量结果，数据显示在3.5km/s速度和地表常压环境下，模型在距其约22倍特征长度位置产生的峰值超压达到约35kPa。采用理想气体假设的简化计算仿真得到的音爆波形与试验测量结果相似，但峰值超压高于实测结果。

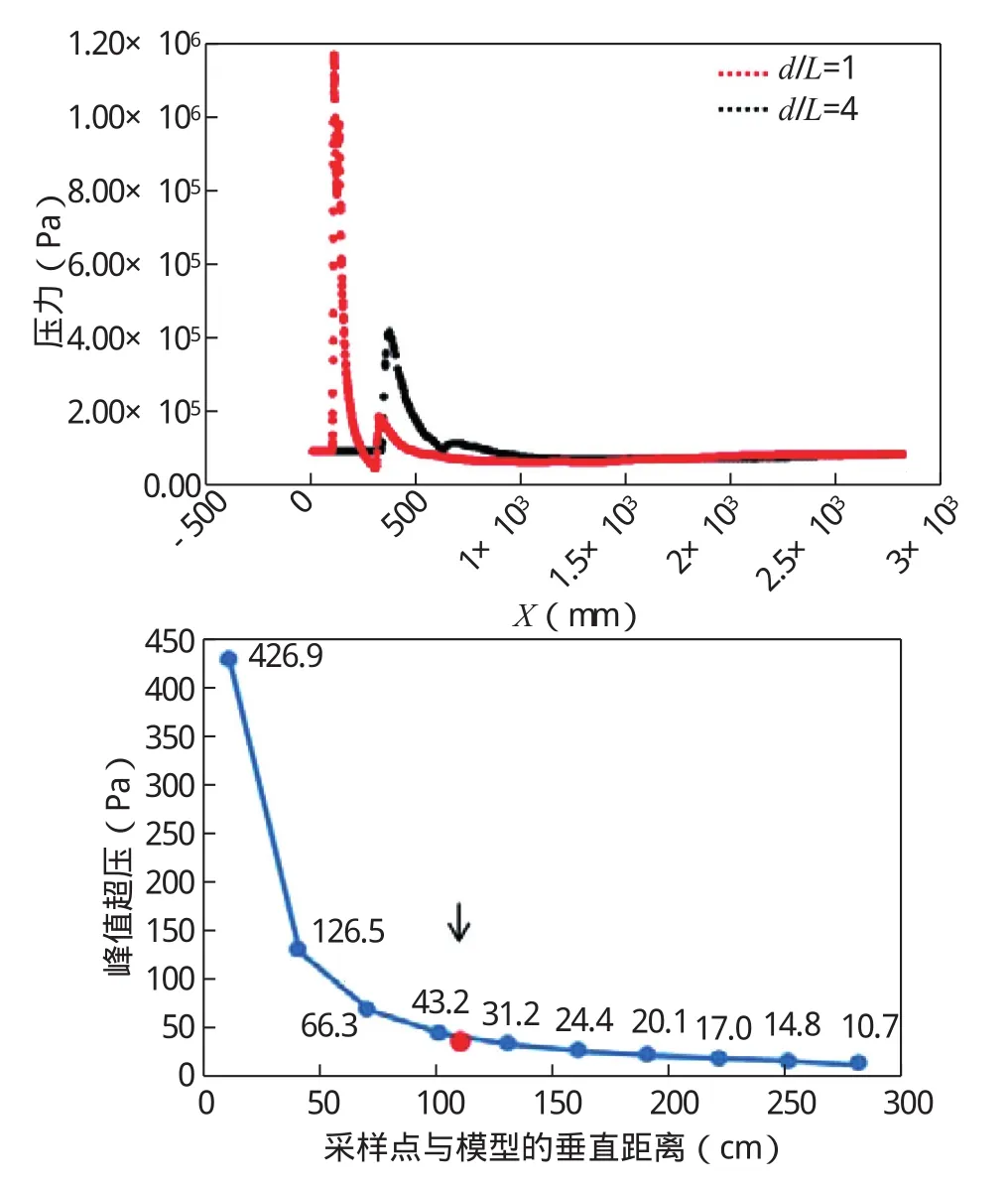
图12 CFD计算得到的近场音爆波形及峰值超压Fig.12 Near field sonic boom waveform and peak overpressure from CFD computation

后续，需从以下几个方面进一步建立和完善陨石音爆计算方法和试验手段，并开展对比验证。一是发展考虑陨石材料、形状和烧蚀特性的近场数值计算方法；二是开展更大测量范围和更多采样点的陨石音爆模拟试验，获取更加丰富和准确的实测数据；三是探索从近、中场到远场的音爆传播计算方法并开展对比验证。