一类极小值复合向量函数Clarke 广义Jacobi 的有效算法
宋林森
(河南科技学院数学科学学院,河南新乡453003)
混合互补问题是一个重要的优化问题,在经济计划、工程设计、交通运输及生产管理等多方面都有着广泛的应用.截至目前,对于混合互补问题已经有许多有效算法[1-7].由于一般类Lipschitz 函数的广义微分不易计算,因此多将混合互补问题借助于中值函数或KKT 最优条件等价转化为非光滑方程组,但对其算法研究多基于构造(或已有)光滑化函数的传统算法改进,基于非光滑函数广义微分计算的非光滑算法研究相对少见.基于此,本文将以混合互补问题的两种不同转化形式为应用背景,给出求解一类极小值复合向量函数广义Jacobi 的有效算法.
1 预备知识
考虑混合互补问题(MCP):求向量 使其满足
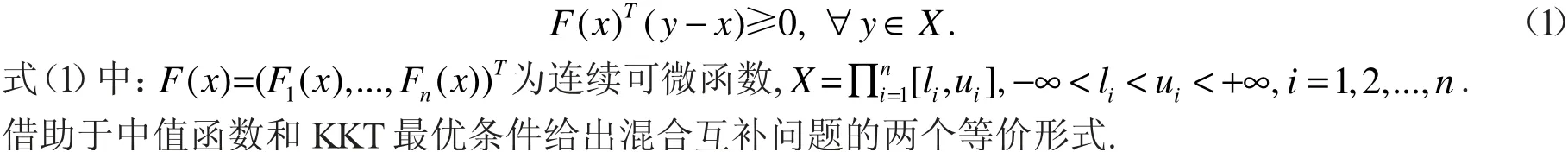
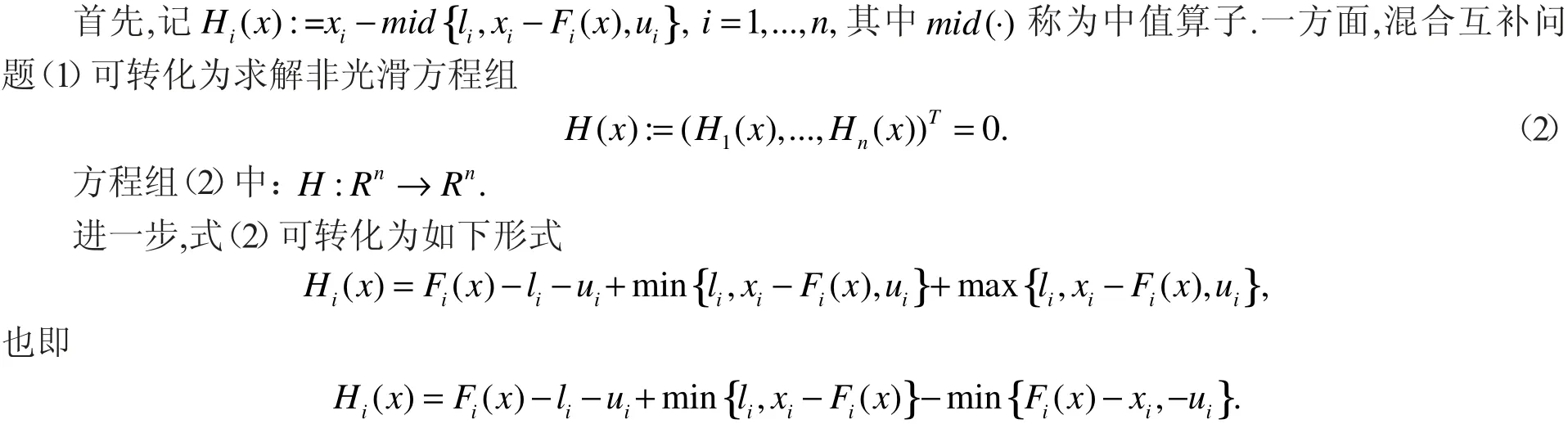
另一方面,由于混合互补问题(1)是盒子约束优化问题.基于一般约束优化问题的局部最优KKT 条件可知,该问题的最优解也满足如下方程组

2 一类极小值复合函数Clarke 广义Jacobi 的计算方法
混合互补问题(1)借助于中值函数或KKT 最优条件,都可以等价转化为分量为极小值线性函数的非光滑方程组.由于一般类Lipschitz 函数的广义微分不易计算,而其又为非光滑可执行算法实施的保证,本节给出了求解一类极小值复合函数Clarke 广义Jacobi 的计算方法.
首先,记
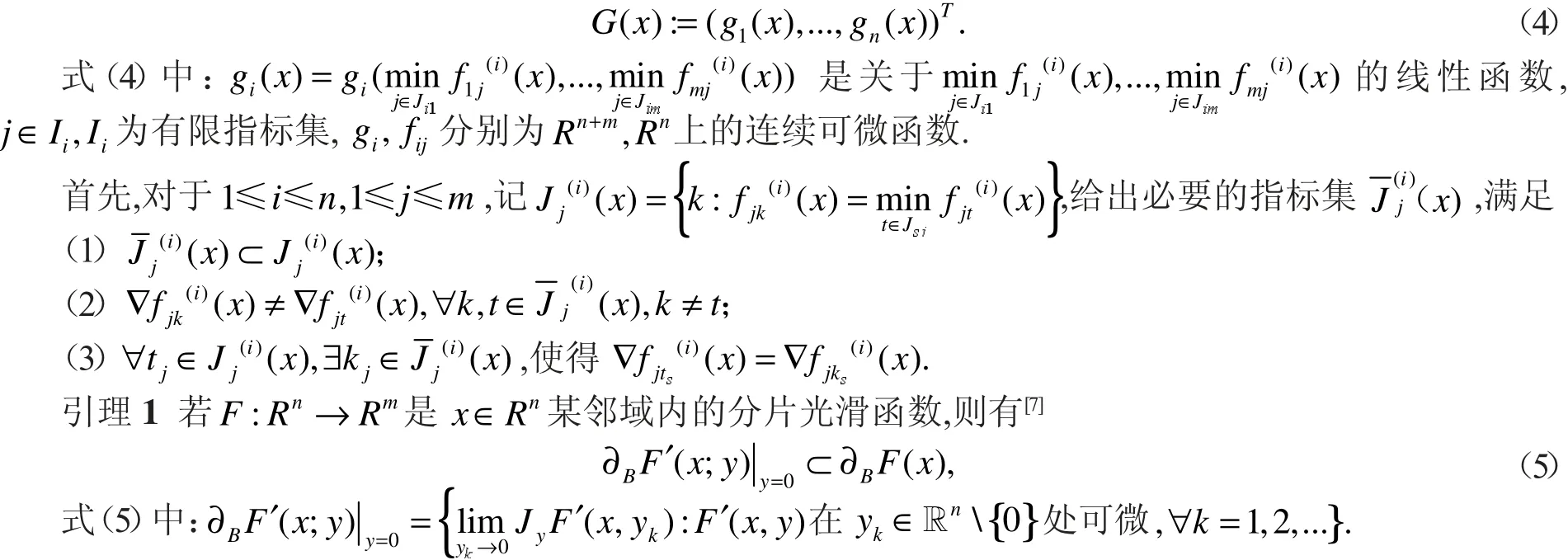

3 算例
结合两个例子,给出混合互补问题两类不同等价转化形式下,对应非光滑函数B 微分(Clarke 广义Jacobi)中元素的具体计算方法.
例1 考虑混合互补问题.设[ l , u ] =[0,5]4,


4 小结
Clarke 广义Jacobi 的计算是非光滑优化数值方法中的必要子算法.本文以混合互补问题的两个等价形式为应用背景,对一类特殊极小值复合向量函数Clarke 广义Jacobi 计算方法进行了研究,并结合算例给出了具体的计算步骤.然而,由于混合互补问题应用广泛,至今已形成许多有效的计算方法,将Clarke广义Jacobi 的计算应用于求解此类问题的非光滑算法中,是否具有良好的运算结果,还需要进一步研究.

