基于LSTM 神经网络的苹果价格预测模型
张顺利,王小东,李艳翠
(1.河南科技学院信息工程学院,河南新乡453003;2.山东聊城第二中学,山东聊城252000)
苹果是世界上最受欢迎的水果之一,中国的苹果种植面积和产量均占世界50%以上.但是由于受生产成本、市场供求关系、政策导向以及国际市场变动等因素的影响,苹果的市场价格时常出现较大的波动.苹果价格的波动不仅会影响百姓的生活质量和果农收入,还会影响市场其他农产品的价格走势,进而引发社会问题.
从相关文献来看,早期农产品价格的预测方法主要采用基于计量统计的时间序列预测方法,根据农产品历史价格数据建立统计模型,预测其未来的价格走势.唐占彪等[1]使用甘肃省重点农产品市场信息采集分析系统的价格监测数据,采用乘法原则对马铃薯等蔬菜价格序列进行季节分解,并根据季节调整后的蔬菜平均价格建立了ARIMA 模型,完成了马铃薯等22 种大众蔬菜2015 年各月份的整体平均价格预测.韩雯[2]以贵州省辣椒的月价格为实验数据,使用季节分解方法剔除季节因素,形成新的时间数据序列,构建的非平稳时间序列ARIMA 预测模型,能较好地预测辣椒的月价格趋势,将价格的预测值与实际值的相对误差控制在9%以内.刘峰等[3]根据白菜的历史价格数据,构建非平稳时间序列ARIMA(p,d,q)模型预测白菜未来的月价格.这种基于统计思想的时间序列模型,单纯依靠农产品的历史价格为研究对象进行数据的分析与预测,未考虑影响价格的多种因素,而且这种预测方法在建模之前需要对数据进行差分、分解等工作,使预测的过程更加复杂.近年来,神经网络模型由于其可以自动学习数据特征、灵活考虑多种因素等优点得到了广泛应用.贾宁等[4]采用双重注意力机制与长短期记忆神经网络相结合的方式,选择天气变化作为价格影响因素的特征,预测了未来一周内蔬菜类产品的价格指数.刘雪等[5]研究鸡蛋价格序列特征后,根据其非线性、季节性和周期性变化的特征,提出了一种基于时间序列季节性分解和长短期记忆网络的组合预测模型,首先使用STL 方法分解鸡蛋价格,将价格中的趋势成分及剩余成分用LSTM 模型进行预测,其预测结果表明模型的预测能力优于ARIMA 模型.但目前在苹果的价格预测方面,还未有比较成熟的神经网络模型应用.基于此,本文构建了一种基于LSTM的神经网络模型进行苹果价格的预测.为了验证预测模型的性能,本文采用先前比较成熟的差分整合移动平均自回归(Autoregressive Integrated Moving Average Model,ARIMA)模型作为基线,进行了对比实验,实验结果验证了神经网络预测模型的有效性.
1 模型及算法
选取豫南阳果品批发交易中心的山东烟台红富士价格为研究对象,分析影响苹果市场价格波动的相关因素,选取苹果历史价格、替补水果(香蕉、橙子)价格、居民消费指数为实验特征,将时间序列问题转化为可监督学习问题,构建基于LSTM的神经网络价格预测模型,实现对苹果市场价格的预测.
1.1 价格影响因素的选定
苹果市场价格的波动是由多种因素引起的,根据市场调研和相关经济规律研究学者[6-8]的研究文献分析,我国苹果的市场价格主要与以下5 个因素相关:
(1)苹果的历史价格.计量经济学家们指出,商品的历史价格蕴含着丰富的信息,将会对未来商品的价格产生周期性或者波动性影响.
(2)替补水果价格.根据相关学者的研究成果分析,苹果的替补水果的价格会影响对苹果的市场需求量,也会引起苹果的市场价格波动[9].本文使用回归模型,采用脉冲响应函数和方差分解方法对苹果的替补品香蕉、葡萄、橙子等进行分析实验.根据实验结果选定香蕉、橙子的价格为苹果价格预测特征的组成部分.
(3)居民消费水平.商品经济学的收入效应理论指出,居民消费水平的变化影响着居民的购买能力,购买能力的变化会引起商品价格的波动.
(4)季节性周期变化.生鲜水果由于所处时期的不同,价格会存在明显的波动.预测日期的月份、日期以及是星期几等因素都会对苹果的价格产生影响.另外在苹果的成熟季节价格会偏低,而大型节日价格就会有增高的波动.
(5)突发事件.自然灾害、流行疾病等突发事件能引起商品市场价格的大幅度波动,如最近的新冠肺炎,水果生鲜的价格都有很大的波动.但是这些事件对市场价格的影响较为复杂,至今没有比较可行的建模方法,因此在现阶段的研究工作中不予考虑.
1.2 基于LSTM 的苹果价格预测模型构建
根据影响苹果价格因素的学习分析结果和苹果价格的季节性、周期性波动特征,构建了图1 所示的基于LSTM的苹果价格预测模型,模型由特征输入层、双向长短期记忆层、结果输出层3 个层次组成.将原始特征数据拼接成一个特征向量,拼接后的特征向量用作双向长短时记忆层的输入,经过该层计算后输出苹果的价格表示,最后在结果输出层对价格序列进行整体优化,输出下一个时间点苹果的预测价格.

图1 基于LSTM 的苹果价格预测模型Fig.1 Apple price forecasting modelbased on LSTM
1.2.1 特征输入层 根据影响苹果价格的因素分析结果,设计特征输入层如图2 所示,输入特征向量由历史价格向量、替补水果信息向量和居民生活消费指数向量3 个部分拼接组成,因为苹果的周期性、季节性特点可以在历史日期中提取,所以和历史价格特征放到一起,不再单独列出.

图2 特征输入层向量组成Fig.2 Feature vectors in input layer
图2 中,历史价格向量包括:日期的年份+日期的月份+日期信息的天数+星期几(一周中的第几天)+价格+是否是法定假日.例如日期为“2019-03-02”,则历史价格向量为:2019+03+02+6(表示周六)+当天苹果价格+“否”,共6 个特征.
可替补性水果(香蕉、橙子)的信息向量包括:香蕉上个月本日价格+香蕉上个月均值价格+橙子上个月本日价格+橙子上个月均值价格4 项内容.居民消费价格指数向量包括:去年居民消费生活指数+上个月份居民消费指数两部分数据.特征输入层向量维度为12 维.
为了减少特征数据数值的差异性,对所有的特征均按公式(1)进行了了归一化处理.

式(1)中:X 表示原始的特征数据,Y 表示归一化处理之后的结果数据,Xmax和Xmin分别表示原始特征数据列中的最大值和最小值.
1.2.2 双向长短期记忆层 双向长短期记忆网络(BLSTM)是一种类似于循环神经网络(RNN)的网络模型,和循环神经网络的区别在于它使用LSTM结构单元[10]替代RNN 网络中的隐藏单元.基于长短期记忆网络的神经网络模型由于克服了传统RNN 模型中存在的梯度爆炸或者梯度消失问题[11-12],被广泛地应用到了很多领域.LSTM单元通过输入门、记忆单元、遗忘门来控制参与网络中的信息继续参与计算或者被丢弃.其计算公式为

在一个输入的价格特征向量序列{x1,x2,…xn},t∈1,2,…n 中,每一个时间点的特征数据对应一个LSTM单元,其输入为{xt,ht-1,ct-1}3 个变量,输出为{ht,ct}.公式中的σ 是激活函数,it、ft、ot、ct分别表示神经网络在t 时刻的输入门、忘记门、输出门和记忆门;wi、wf、wc表示不同的权重矩阵,bi、bf、bc为偏置向量,这两组值通过神经网络训练学习得到.在每一个t 时刻,ft计算哪些没用的特征信息在当前的单元中将被放弃掉,it决定哪些新的输入特征应当被存放在当前的记忆单元ct中,ot表示哪些信息将被输出到当前的ht中.t 时刻LSTM的输出向量{ht,ct},结合t+1 时刻的特征向量xt+1输入到下一个LSTM单元.
如图1 所示,BLSTM网络首先对每个输入的价格特征向量采用从左到右地顺序(Forward)计算,然后再按照从右到左地顺序(Backward)循环回来进行计算,每一个t 时刻的价格特征向量经过计算后得到两种不同的隐藏层向量表示:和这两个向量的拼接得到双向长短时记忆层的输出,其计算公式为

式(3)中:tanh 为激活函数,wh为权重矩阵,bh表示偏置向量.
1.2.3 结果输出层 对双向长短期记忆网络层计算的结果进行整体序列优化,输出下一个时刻的预测价格.
1.3 模型训练
由于要进行苹果的月价格、周价格和日价格数据预测,训练了3 个神经网络模型,每个神经网络模型的输入序列长度各不相同,月价格预测模型序列输入长度为12,周价格预测模型序列的输入长度为48,日价格预测模型序列输入长度为30.选用平均绝对误差(MAE)为损失函数,每个模型选取的最优向量维度和学习率也各不相同,在结果部分有详细地说明.对于每次LSTM模型训练,我们通过每次迭代的损失函数对训练效果做初步的判断.随着训练进行,损失函数逐渐减少,最后得到最优值,损失函数趋于平稳.
2 实验及分析
2.1 实验环境
研究的程序开发环境为Pycharm Community Edition(python 3.7),使用Tensorflow 提供的LSTM神经网络包.训练过程中,采用随机梯度下降模型AdaGrad,为了减轻模型的过度拟合,在BLSTM层的输入输出部分增加了Dropout.
2.2 数据来源
研究中所使用的苹果、香蕉和橙子的价格数据由作者在全国农产品商务信息平台上(http://nc.mofcom.gov.cn/)上爬取的豫南阳果品批发交易中心的价格数据得到.居民消费指数数据从中华人民共和国统计局网站(http://www.stats.gov.cn/)上查询得到.本次试验选取的苹果历史数据的时间范围为2016年4 月到2020 年4 月,价格数据为1 152 条,其价格单位为元/500 g.
2.3 评测方法
本实验选取时间序列数据预测中常用的4 个客观评价标准,进行数据分析.
(1)平均绝对误差(MAE,),由式(4)计算

(2)均方误差(MSE,),由式(5)计算

(3)均方根误差(RMSE,),由式(6)计算

(4)平均绝对百分比误差,由式(7)计算

2.4 实验结果
本文进行了3 组苹果价格的预测实验,分别为月价格、周价格和日价格数据预测.
2.4.1 苹果月价格预测 在价格预测模型中,LSTM 网络的输入向量大小设置为100 维,学习率选取为0.03,正则化参数为10-8,Dropout 值为0.3,进行了苹果的月价格预测,预测结果见图3.
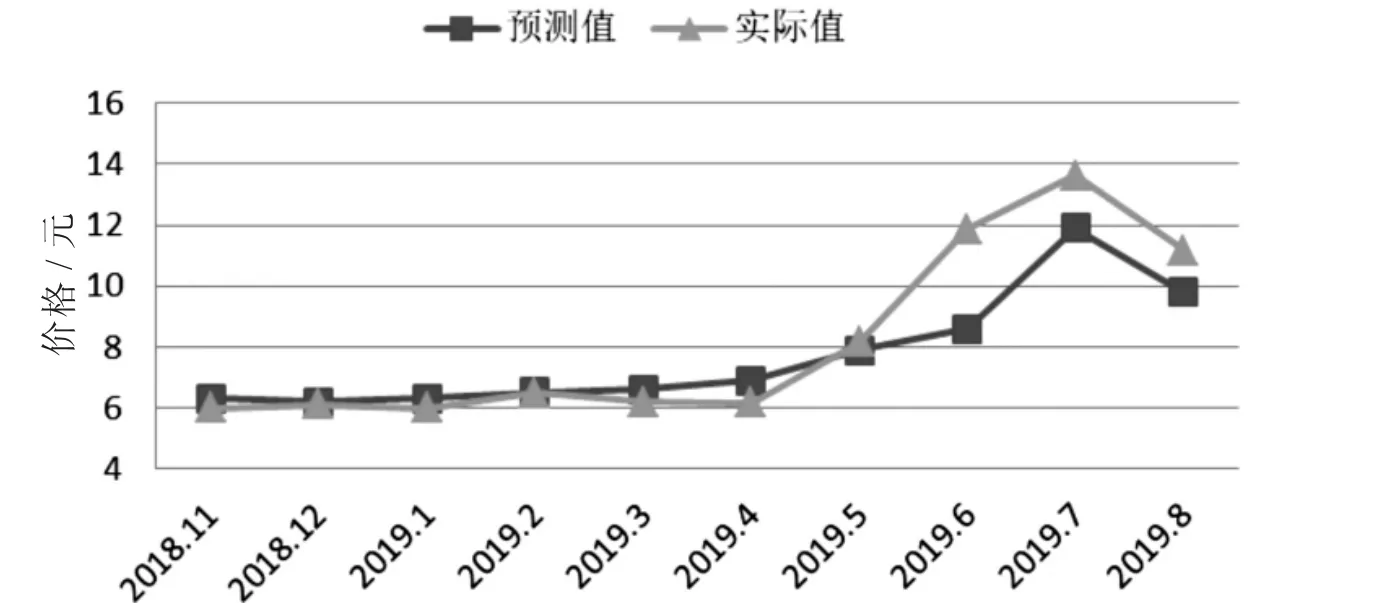
图3 月价格数据预测和实际数值对比Fig.3 Comparison of the forecast and actual value of the monthly price data
2.4.2 苹果周价格预测结果 使用价格预测模型,将LSTM网络的输入向量大小设置为300 维,学习率选取为0.03,正则化参数为10-8,Dropout 值为0.5,进行了苹果的周价格预测,预测结果见图4.

图4 周价格数据预测和实际数值对比Fig.4 Comparison of the forecast and actual value of the weekly price data
2.4.3 苹果日价格预测结果 使用价格预测模型,将LSTM网络的输入向量大小设置为200 维,学习率选取为0.05,正则化参数为10-8,Dropout 值为0.3,进行了苹果的日价格预测,预测结果见图5.

图5 日价格数据预测和实际数值对比Fig. 5 Comparison of the forecast and actual value of the day price data
2.4.4 统计分析 将基于LSTM的神经网络模型的预测数据与传统的ARIMA 模型预测数据进行统计分析,得到的比较结果见表1.

表1 模型预测结果误差对比Tab.1 Error comparison of model prediction results
由表3 可知,基于LSTM的神经网络预测模型除了个别数据的个别评价标准外,均优于ARIMA 模型.因为使用LSTM神经网络模型,可以兼顾数据序列的平稳和非平稳特性特征,LSTM通过对数据的学习训练,可以较好地学习到非平稳时间序列的隐含特征,提高预测的准确度.
3 小结
本文以豫南阳果品批发交易中心的烟台红富士价格为研究对象,分析了当前农产品价格预测的相关理论和技术,在此基础上提出并构建了基于LSTM神经网络的苹果价格预测模型.研究沿用以往的分析方法确定了影响苹果价格的特征,然后对影响价格的特征进行向量化处理,输入BLSTM网络,计算出苹果未来的预测价格,实验总共训练了3 个预测模型.经测试和统计分析证明:本文的神经网络模型既没有损失细节信息,也没有损失整体趋势的价格信息,提高了预测价格的准确度.
在未来的工作中,我们将针对现有的特征做进一步的实验分析,细化调整各个因素之间的权重,优化模型参数,以降低预测数据与真实值之间的误差.

