融合巴氏系数的加权Slope One算法

刘金梅，舒远仲，张尚田，唐小敏，刘文祥

(南昌航空大学 信息工程学院，江西 南昌 330063)

0 引 言

传统的推荐算法主要有基于内容的算法、基于知识的算法、协同过滤算法和混合算法[1]。协同过滤算法应用最广泛，主要包括基于用户和基于物品的协同过滤[2]。slope one算法[3-4]是一种基于物品协同过滤算法，它简洁、容易实现、执行效率高，主要依据项目评分差值预测，当面对庞大的数据集时，无法较好地处理稀疏数据。因此，许多学者对其进行了改进，如：刘毓等人[5]考虑到评分用户数量对预测结果存在影响，提出一种加权slope one算法，该算法提高了预测精度；向小东等人[6]利用项目偏差对未评分的数据进行填充，再使用协同过滤算法；由于加权slope one算法未考虑用户与用户或项目与项目自身关系，王潘潘等人[7]将协同过滤算法与加权slope one算法相结合，通过用户相似度寻找与目标用户最相近的K个邻居，根据邻居对项目的评分进行预测；李桃迎等人[8]不仅考虑了用户相似度还考虑到用户兴趣变化，用遗忘函数与邻居相似度改进加权Slope one算法，进一步提高了精确度；文献[9-10]考虑项目相似性对结果的影响，根据不确定K近邻矩阵中的项目相似性，动态选择每个项目的邻域，然后计算邻域中的项目评分偏差，最后再用线性模型进行预测；陶志勇等人[11]通过用户与项目属性改进相似度，引入用户属性-项目类型偏好权重因子，利用天牛须搜索算法调整兴趣度预测；Zhao等人对上述三人的算法进行了融合，考虑用户和项目相似度并将其都作为权重因子融合到加权slope one算法[12]。

上述改进算法中，相似度的度量都依赖共同评分。当数据稀疏时，皮尔逊相关系数计算性能较差；Jaccard系数仅考虑两者是否有共同特性，不能衡量具体评分数值差异。Bobadilia等人[12]通过获取奇异性信息，提出奇异性相似度测量，相比传统的相似度测量，提高了预测质量，但在数据稀疏时，计算的相似度较差。

因此，该文对相似度计算方法进行改进，提出一种融合巴氏系数的相似度计算方法。首先用Jaccard相似度计算全局相似度，Pearson相关系数计算用户局部相似度，其次用巴氏系数优化用户局部相似度，然后再引入参数α将两者融合获取最终的用户相似度，参数α的引入可以更好地衡量各个相似度在最终相似度中所占的比重。由于要对未知项目进行预测，所以再根据相似度排序选择前K个用户作为目标用户的近邻，再计算近邻用户对项目的评分偏差，最后结合目标用户的评分用加权slope one算法进行评分预测，由于项目相似度对预测也存在影响，因此用巴氏系数计算项目相似度并将其作为权重对预测评分进行改进。

1 几种slope one算法

1.1 slope one算法

slope one算法是一种线性模型，即f(x)=ax+b，可由项目x的值预测出f(x)，b为项目间评分差异值。如表1所示，预测U3对A的评分。

表1 用户对项目的评分

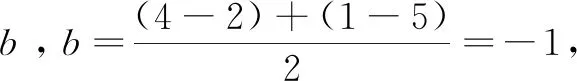
slope one算法的工作流程如下：

(1)计算偏差。

项目之间的偏差计算如下：

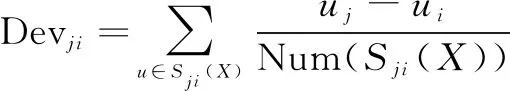
(1)

其中，ui、uj表示用户u对项目i、j的评分；Sji(X)表示评价项目i、j的用户集合；NumV(Sji(X))表示用户数量。

(2)预测。

根据步骤1计算出的评分偏差，再加上用户u对项目的评分预测出目标项目j的评分，公式如下：

(2)

其中，Num(Rj)表示所有用户评过分的项目集合。

1.2 Weighted slope one算法

slope one算法仅考虑评分，未考虑评分用户数量对偏差计算的影响。对同一个项目评分用户数量越多，计算的偏差越精确，因此为平衡每个用户对评分的影响，进行加权处理，改进后的公式如下：

(3)

2 改进的加权slope one算法

2.1 相似度计算方法分析

传统相似度计算方法[13-14]有余弦相似度、修正余弦相似度、皮尔逊相关系数、Jaccard相似度。

设m个用户U={U1,U2,…,Um}和n个项目I={I1,I2,…,In}组成的用户-项目评分矩阵，用户Ui对项目Ij的评分用Rij表示，具体如表2所示。

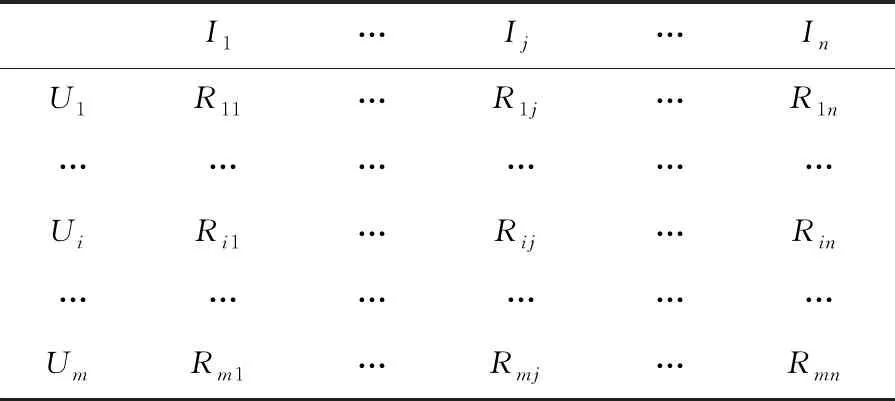
表2 用户-项目评分

(1)余弦相似度。

余弦相似度(cosine similarity)用向量夹角的余弦值表示个体间差异。

设两个用户u、v，Iuv为用户所有评分的项目集，Rui、Rvi为用户u、v对项目i的评分，则两个用户间的余弦相似度的计算公式如下：

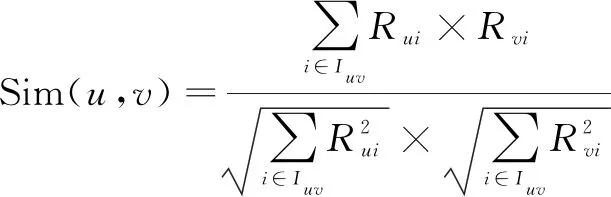
(4)

(2)修正余弦相似度。

由于余弦相似度未考虑评分数值对结果的影响，所以产生了修正余弦相似度(adjusted cosine similarity)，本质是在计算时减去用户评分的平均值。计算公式如下所示：

(5)

(3)皮尔逊相关系数。

皮尔逊相关系数(Pearson correlation coefficient，PC)用来衡量两个变量间的相关程度，取值在[-1，+1]之间。计算公式如下：

Simpcc(u,v)=

(6)

(4)Jaccard相似度。

Jaccard相似度仅考虑个体间是否具有共同特征，没有考虑评分数值大小，具体公式如下：

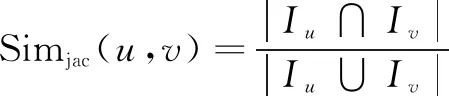
(7)

其中，Iu、Iv分别表示用户u、v对项目评分的集合。

(5)巴氏系数。

巴氏系数(Bhattacharyya coefficient，BC)[15-17]在信号、图像以及模式识别等领域使用较多，可以用来测量样本间的相关性。设p1(x)和p2(x)为同一离散区间X上的两个概率，则计算公式如下：

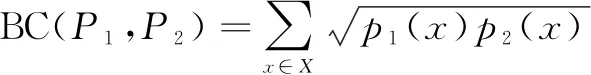
(8)

其中，p1(x)、p2(x)是评分矩阵中的已知评分数据，Pu、Pv分别表示用户u和用户v的评分，则用户u和用户v的巴氏系数相似度计算公式如下：

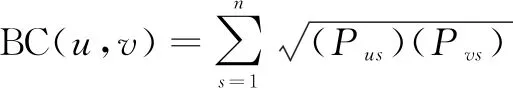
(9)

设用户u对项目的评分为u=(2,3,0,1,1,4)T，用户v对项目的评分为v=(1,0,3,2,1,5)T，评分范围为0～5分，则用户u和用户v使用巴氏系数计算的相似度为：

0+0=0.8

(10)

通过对上述相似度计算方法的分析，发现皮尔逊相关系数在数据稀疏时计算性能较差；Jaccard相似性虽然计算了全局相似度，但是仅考虑项目间的共同特征，没有考虑评分数值大小；而余弦和修正余弦相似度都依赖共同评分；巴氏系数不仅可以在数据稀疏时计算相似度，而且可以分析用户关联性。因此，下面将用巴氏系数来改进相似度。

2.2 相似度计算方法改进

由2.1节分析可知，当共同评分很少或者没有时，传统相似度计算性能较差，因此该文利用巴氏系数优化皮尔逊相关系数，并与Jaccard相似性进行融合得到最终用户相似度。

首先，用皮尔逊相关系数计算用户局部相似度，当数据较少时计算的性能较差，所以用巴氏系数分析用户相关性，将作为影响因子加入到局部相似度中得出用户新的局部相似度。公式如下：

Simloc(u,v)=Simpcc(u,v)BC(u,v)

(11)

其次，用Jaccard相似性计算全局相似度，将优化的局部相似度和全局相似度进行融合，设置参数α，参数α用来凸显不同相似度在最终相似度中的权重。公式如下：

Sim(u,v)=αSimjac(u,v)+(1-α)Simloc(u,v)

(12)

上述两式经处理获得最终的用户相似度，公式如下：

Simpcc(u,v)=αSimjac(u,v)+

(1-α)BC(u,v)2Simpcc(u,v)

(13)

2.3 预测评分的改进

根据2.2节计算出的用户相似度，先降序排列后根据顺序挑选前K个用户放入邻居集合S(K)中；再从邻居集合中筛选出评价过目标项目的邻居用户，计算出目标项目与邻居用户评过分项目的评分偏差Devji；最后通过偏差与目标用户的评分用加权slope one算法预测，公式如下：

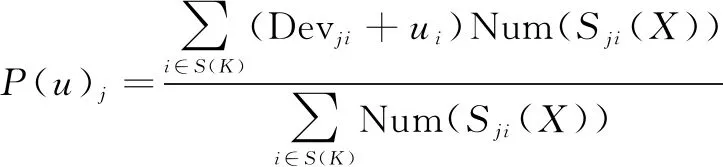
(14)

由于式(14)中仅仅考虑了用户评分对预测结果的影响，未考虑项目本身对其的影响，因此，在评分预测时又考虑项目相似度。对于项目相似度计算，该文使用巴氏系数。首先计算所有的项目相似度；然后找出邻居集合S(K)中前K个邻居所评分的项目集合；再计算目标项目j与邻居项目i之间的相似度BC(i,j)；最后将所得的项目相似度作为权重因子，加入到式(14)中得出最终的预测评分。公式如下：

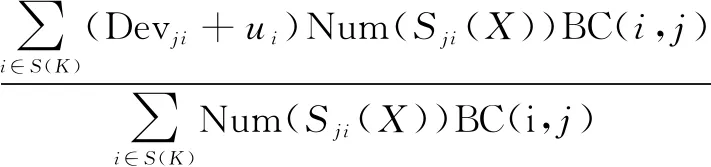
(15)

将项目相似度作为权重因子加入到预测公式中，一方面可以削弱项目相似度低对预测结果的影响，项目相似度高被忽略的现象；另一方面考虑用户和项目相似度，可以使结果更准确。

2.4 算法流程

输入：用户-项目评分矩阵R，参数α、邻居数K。

输出：目标用户u对项目i的预测评分。

算法步骤如下：

步骤1：创建用户-项目评分矩阵R，并根据给定的数据集填充矩阵R。

步骤2：根据评分矩阵R，利用式(6)计算用户局部相似度，式(7)计算用户全局相似度。

步骤3：利用巴氏系数(式(9))分析用户相关性，计算项目间相似度。

步骤4：用步骤3计算出的巴氏系数优化式(6)的局部相似度，并与式(7)的全局相似度相融合，设置参数α线性融合得到最终的用户相似度。

步骤5：根据步骤4得到的最终用户相似度，将相似度进行降序排列再选择前K个作为用户邻居，放入邻居集合S(K)中。

步骤6：由步骤5的邻居集合S(K)，根据最近邻居用户对未知项目的评分来预测目标用户对项目的评分，最后再将步骤3中的项目相似度加入到式(14)中，最后使用式(15)预测出最终目标用户对项目的评分。

3 实验结果与分析

3.1 数据集

采用MovieLens数据集进行测试(https://grouplens.org/datasets/movielens/)，其中用户个数943，电影为1 682部，总共评分数为100 000条，评分范围为1～5分，数据的稀疏程度为0.063。数据集划分比例为8∶2，用五折交叉法来进行实验。

3.2 评价指标

文中算法的预测质量由平均绝对误差(mean absolute error，MAE)和均方根误差(root mean square error，RMSE)来衡量，公式如下：

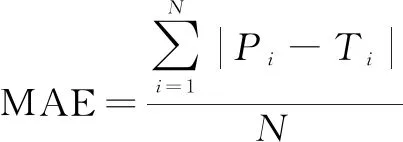
(16)

(17)

其中，Pi为预测评分，Ti为测试集中的实际评分，N为测试集中评分的总数。

3.3 结果分析与比较

3.3.1 确定参数α、K的值

在改进相似度时，用巴氏系数优化皮尔逊相关系数获得用户局部相似度，用Jaccard相似性计算用户全局相似度，最后在相似度融合时，使用参数α来组合优化的用户局部相似度和用户全局相似度。参数α用来凸显不同相似度在最终相似度中的权重，将参数α设置为[0.1,1]，步长为0.1，选择的邻居数K为[10,60]，步长为10。为排除实验结果的偶然性，将6组不同邻居下的值取平均，分析α以及K的变化对MAE和RMSE的影响，实验结果如图1和图2所示。

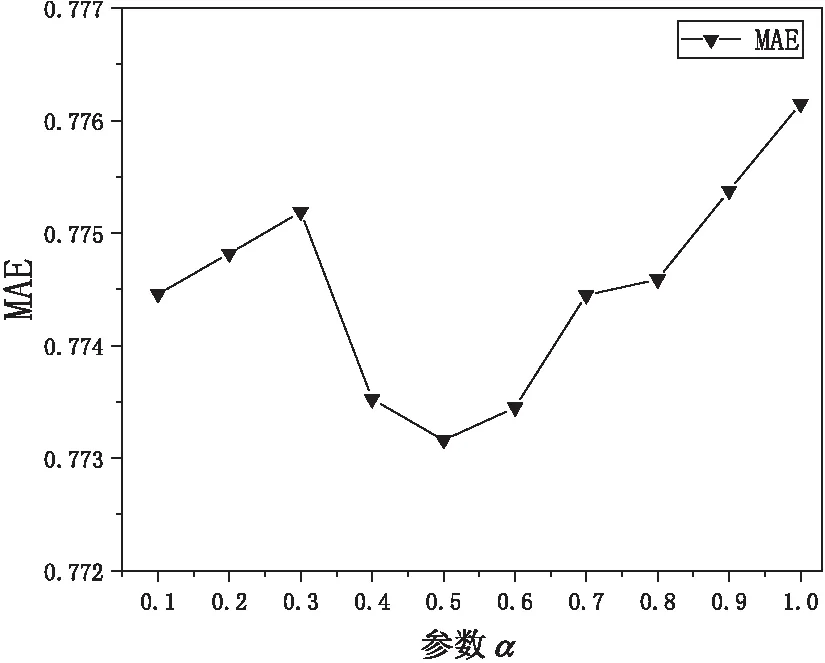
图1 不同参数α对MAE的影响

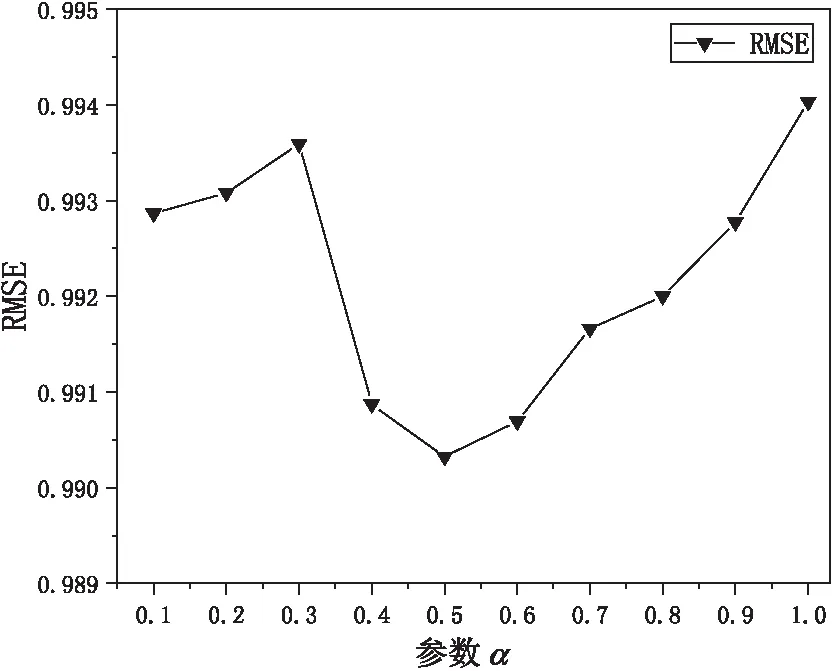
图2 不同参数α对RMSE的影响

从图1和图2可以看出，MAE和RMSE的值随参数α增大而变化，当参数α取值为0.5时，MAE和RMSE均达到最小值，说明此时的效果最佳。因此，在用户相似度改进算法中，在局部相似度和全局相似度融合时，将参数α设置为0.5。

在改进的算法中，邻居数量不同也会影响预测结果，因此，该文选取不同的邻居数量进行测试(K=10,40,80,120,160,200,240,280,320)，每一个K进行5次实验，再对其取平均值作为最终结果。绘制邻居数量K与MAE和RMSE的关系图，如图3和图4所示。

图3 邻居数量K与MAE的关系

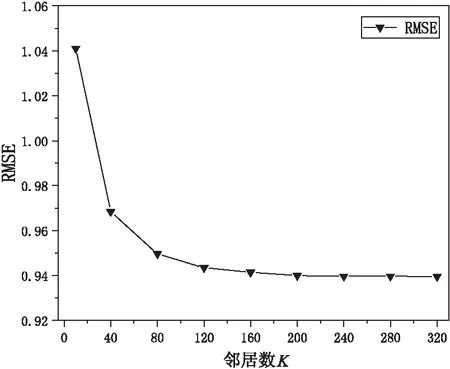
图4 邻居数量K与RMSE的关系

从图3和图4可以看出，随着邻居数量K的增多，MAE和RMSE均先减小后慢慢趋于稳定。因为在邻居数量较少时可用来分析的数据较少，此时产生的误差就偏大；随着邻居数量的不断增多，可利用的数据越来越多，误差逐渐减小直至最后达到某一数值趋于稳定。从图中可以看出，当邻居数K=200时，误差最小，此时预测评分愈加接近真实值。因此，实验选取邻居数量为200进行研究，不仅可以保证良好的预测结果，同时又能够降低计算复杂度。

3.3.2 改进预测公式的算法对比

预测公式的不同，实验结果也会存在差异。该文利用巴氏系数计算项目相似度，将其加入到原始加权slope one预测公式中，将改进后的预测公式与未加入权重因子的未改进预测公式作对比，结果如图5和图6所示。

从图5和图6可以明显看出，改进预测公式的MAE和RMSE值均比未改进预测公式的值小，说明用巴氏系数改进预测公式在某种程度上可以提高预测精度。

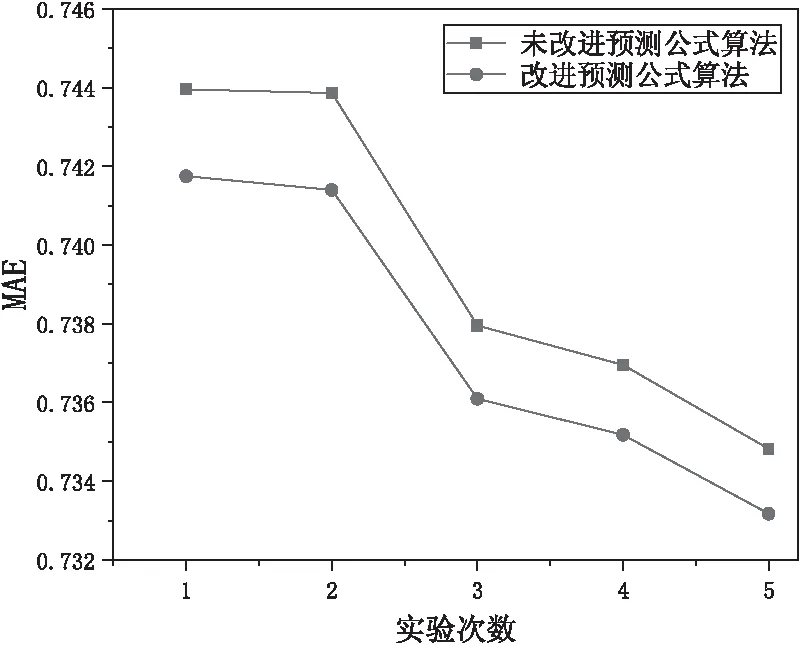
图5 不同预测公式的MAE值

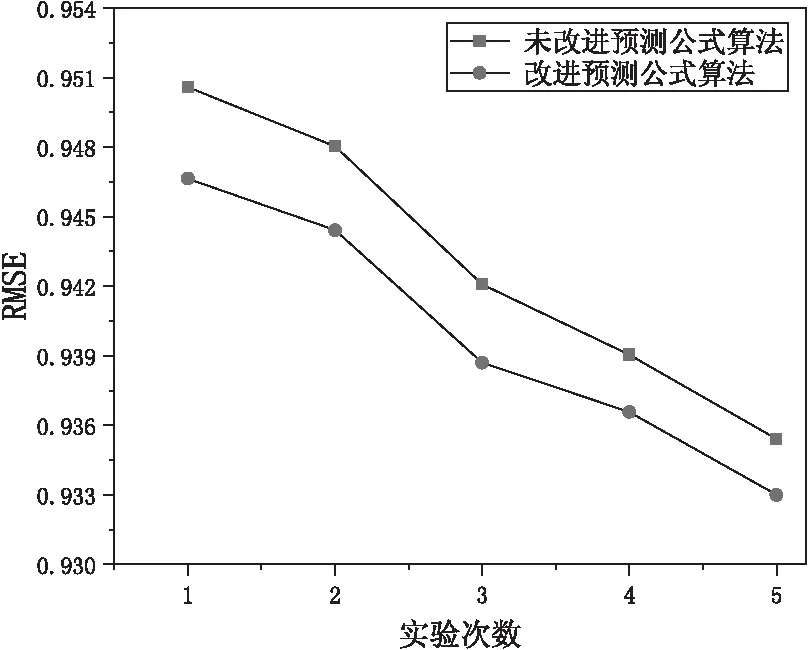
图6 不同预测公式的RMSE值

3.3.3 改进算法与其他算法的对比

利用巴氏系数可以在稀疏数据情况下仍然能够计算相似度，提出用巴氏系数优化皮尔逊相关系数，并与Jaccard相关系数相融合得到一种新的相似度计算方法。通过3.3.1节可知，在相似度融合时，参数α取0.5时可以获得最优用户相似度；在邻居数量K为200情况下，预测结果愈加接近真实值，误差较小，因此，将参数α设置为0.5，邻居数量K设置为200进行实验。将改进的算法(BCWSOA)与文献[18]中基于加权slope one和用户协同过滤的推荐算法(CF_WSOA)、Weighted slope one算法、slope one算法和基于用户的协同过滤算法(UCF)进行比较，衡量指标为MAE和RMSE，实验结果如图7和图8所示。

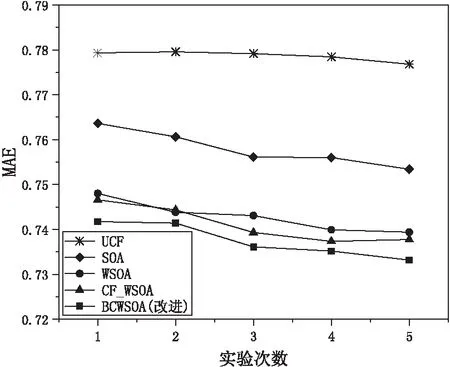
图7 不同算法的MAE值

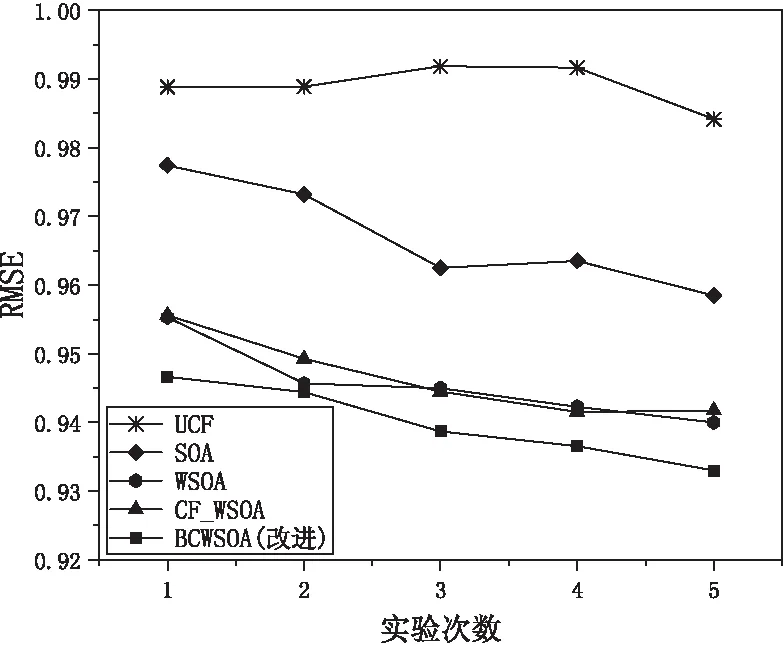
图8 不同算法的RMSE值

从图7和图8可以看出，当参数α为0.5，邻居数K为200时，改进算法BCWSOA的MAE和RMSE值相比于其他几种算法均有所减小，预测准确性有所提高。

4 结束语

该文融合巴氏系数改进相似度的计算方法，解决了用户共同评分很少或者没有的问题。考虑了项目相似度对预测的影响，用巴氏系数计算相似度改进加权slope one算法。与基于加权slope one和用户协同过滤的推荐算法(CF_WSOA)、Weighted slope one算法、slope one算法和基于用户的协同过滤算法(UCF)进行比较，融合巴氏系数的加权slope one算法在预测精确度上均有所提高。