解题思维异构 助力教师思考——一道竞赛题的探究与拓展*

张维明 (江苏省连云港市和安中学 222100)

“解题思维异构”是指联想与问题有密切关联的事实和条件，多角度、多层次、多途径地理解数学问题，厘清知识脉络，构建知识间的有机联系，从不同的视角解决问题，在联想、延伸、变化、拓展中层层深入，抓住问题的本质，尝试创新，触发并提出新的数学问题．[1]本文以2019年江苏省中学生数学竞赛试题(九年级)第12题为例，对基于“解题思维异构”视角的探究、拓展与思考进行阐述，以期抛砖引玉．

1 试题及思路简析

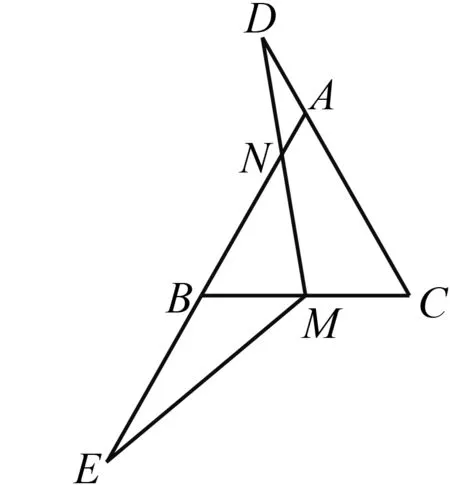
图1

题目如图1，在等边三角形ABC中，点M为边BC的中点，点D,E分别为CA,AB延长线上的一点,MD=ME，N为线段MD与线段AB的交点．

求证：∠BNM=∠BME．

思路1 对于条件MD=ME，笔者想到连结ED，构建等腰三角形MDE，得到∠MED=∠MDE，但是无法与∠BNM及∠BME联系，未能成功求证．

思路2 利用条件点M为边BC的中点，取AC中点P，连结MP，得到等边三角形MCP，求证△EBM≌△DPM，但未能奏效．

思路3 将ME或MD进行转移，构建等腰三角形，利用全等三角形来证明，终于获得突破．

2 证法探究

2.1 转移ME或MD

证法1如图2，延长AC到点F，使得CF=BE，连结MF．因为点M为边BC的中点，所以△MBE≌△MCF，故ME=MF，∠E=∠F．因为MD=ME，所以MD=MF，故∠D=∠F，从而∠D=∠E．因为△ABC为等边三角形，所以∠BNM=∠DNA=60°-∠D，∠BME=60°-∠E，故∠BNM=∠BME．

证法2如图2，因为△ABC为等边三角形，所以∠BAC=∠BCA=60°，故∠DAN=∠MCF=120°．由证法1得∠D=∠F，所以△ADN∽△CFM，所以∠DNA=∠CMF．由证法1中△MBE≌△MCF可得∠BME=∠CMF，且∠DNA=∠BNM，所以∠BNM=∠BME．

证法3如图2，因为△ABC为等边三角形，所以∠BAC=∠ABC=60°，所以∠DAN=∠MBE=120°．由证法1得∠D=∠E，所以△ADN∽△BEM，故∠AND=∠BME．因为∠AND=∠BNM，所以∠BNM=∠BME．

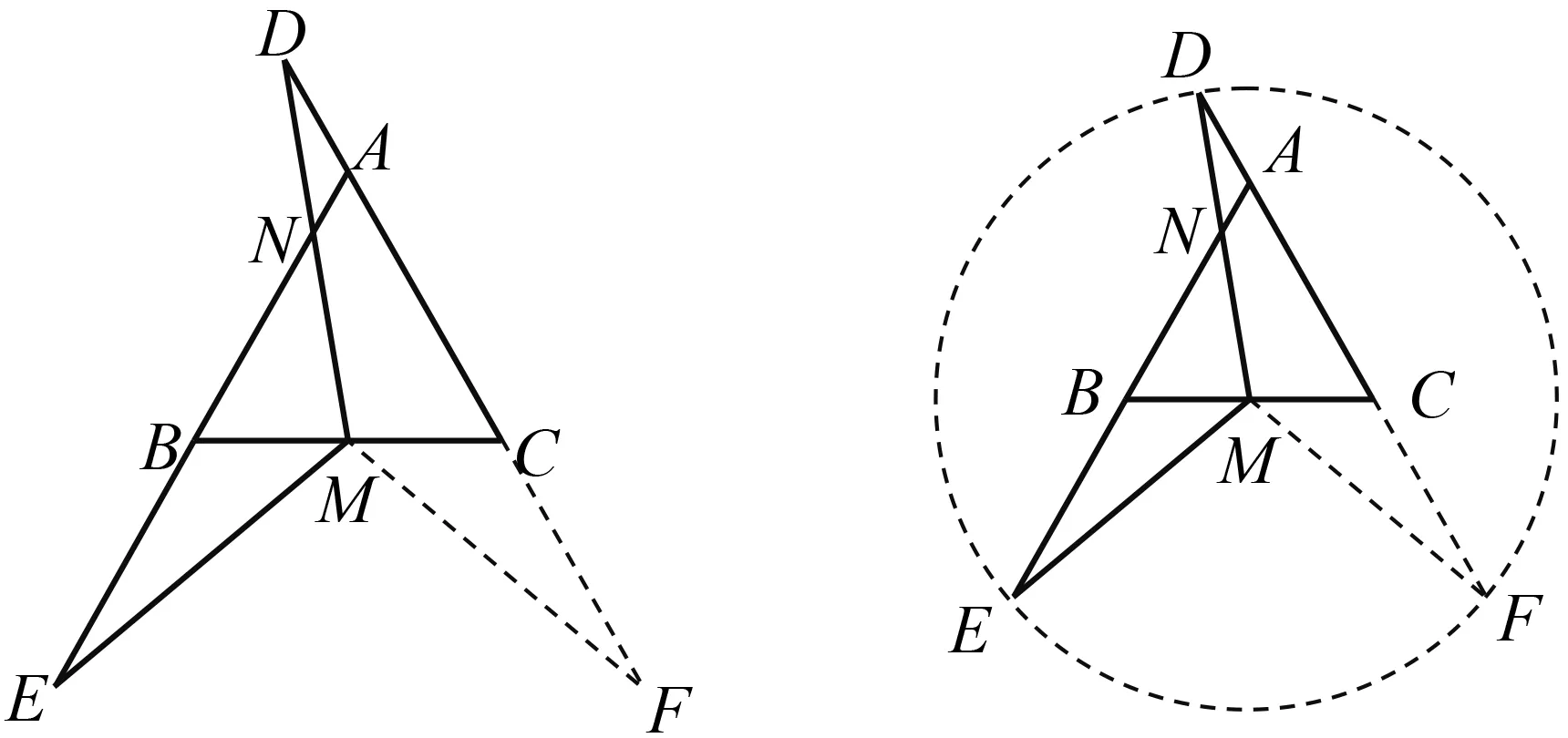
图2 图3

证法4如图3，以M为圆心、MD为半径画⊙M，延长AC交⊙M于点F，连结MF．因为MD=ME，所以点E在⊙M上．因为AC交⊙M于点F，所以MF=MD=ME，以下过程同证法1或证法2或证法3．

分析 因为证法1、证法2、证法3起始过程一样，后续过程大同小异，所以上述四种方法也可以化归成以证法1和证法4为代表的两种方法．本质都是转移ME或MD，构建等腰三角形，利用全等三角形或相似三角形，将∠F或∠CMF作为桥梁联系∠D,∠E或者∠BNM,∠BME．

反思虽然试题标准答案是证法1，证法1也确实非常简便，笔者所带班级学生也完全听得懂，但是笔者阅卷时发现九年级学生却极少用到证法1．笔者调查本班学生获知，证法1不是学生的自然思路，学生无法想到．学生利用对顶角、外角，想到∠BNM=∠DNA=60°-∠D，∠BME=60°-∠E，证明出∠D=∠E即可得到∠BNM=∠BME．由条件MD=ME很容易想到构建三角形全等证明∠D=∠E，这是八年级学生的自然思路．上述思路2就契合这一想法，但是取AC中点P，连结MP，求证△EBM≌△DPM，未能奏效．笔者疑惑：学生证明三角形全等的方法是否选择不当？笔者再次审视思路2，开始新的思路探究．

2.2 开发中点M

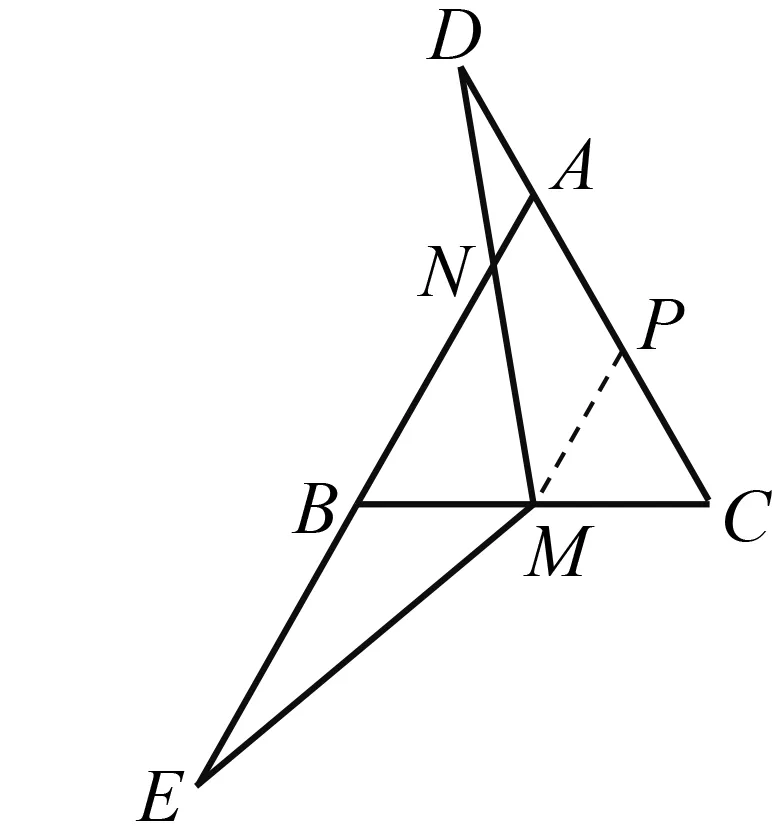
图4

证法5如图4，取AC中点P，连结MP．因为点M为边BC的中点，P为AC中点，△ABC为等边三角形，根据等边三角形的判定方法易证△PMC也为等边三角形．所以MB=MP，∠EBM=∠DPM=120°．因为ME=MD，所以△EBM与△DPM满足了“边边角”的条件．

分析 因为△EBM与△DPM满足的是“边边角”的条件，所以真的无法证明△EBM与△DPM全等吗？苏科版教材在数学活动中引导师生探究“两边和一角分别相等的两个三角形是否一定全等”，师生常常去列举不全等的例子，很少列举全等的例子．教师会强调满足“边边角”的两个三角形不一定全等，其用意是强调“边边角”不能用于判定两个三角形全等，以区别于一定能判定全等的“SAS”等．但不幸的是，因为列举全等的例子太少甚至环节缺失，在部分教师和大部分学生的观念中，概念被偷换成“边边角”(直角除外)一定不全等或者无法证明出全等．笔者和所在班级的学生也被概念偷换所误导，认为满足“边边角”条件的△EBM与△DPM看似全等但无法证明，使得思路2未能奏效．证法5的进一步探究，正是一次消除对“边边角”误解的好机会．

为了理清解题思路，如图5，将△EBM与△DPM从图4中拆解出来，形成下列题中题：

已知在△EBM,△DPM′中，MB=M′P，ME=M′D，∠EBM=∠DPM′=120°．求证：△EBM≌△DPM′．

图5 图6

如图6，将△EBM,△DPM′拼在一起，连结BP．如图7，分别过M,M′作MQ⊥BE,M′R⊥PD，垂足分别为点Q,R．两种方法都可以很快地证明出△EBM≌△DPM′，感兴趣的读者可自行证明．由此说明，满足“边边角”条件的两个三角形有可能全等，也可以证明．

图7

反思实际上，对于满足“边边角”的两个三角形何时全等的话题，一线教师都曾有过相应的探索，文献[2]和[3]对此做了较为详尽的分析和阐述，教师和学生可以阅读获得启发．八年级学习全等三角形初始，教师要多了解“边边角”的多种情况，做到心中有数，指导学生从简单到复杂，在“做”中思维、在“做”中发现、在“做”中积累、在“做”中感悟，从本质上理解“边边角”．

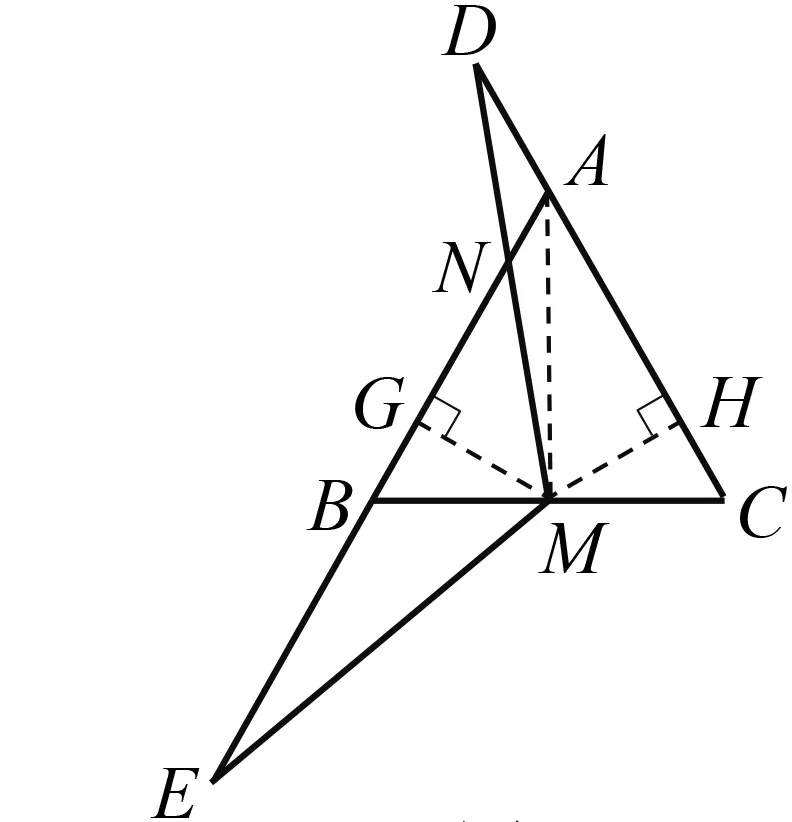
图8

证法5(续) 结合图4，本题选择上述第二种方法证明△EBM≌△DPM．如图8，过M分别作MG⊥AE,MH⊥CD，垂足分别为点G,H．因为∠BGM=∠PHM=90°，∠GBM=∠HPM=60°，MB=MP，所以△GBM≌△HPM(AAS)，所以MG=MH．因为ME=MD，所以Rt△GEM≌ Rt△HDM(HL)，所以∠D=∠E．所以∠BNM=∠BME．

反思证法5中，得到MG=MH是一个关键．观察图8，重新思考MG与MH，会感悟到证法5走了弯路，对中点M开发不足，连结AM，马上就可以得到MG=MH．更简单的证法自然生成．

证法6如图8，连结AM，过M分别作MG⊥AE,MH⊥CD，垂足分别为点G,H．因为点M为边BC的中点，所以AM是△ABC的中线．因为△ABC为等边三角形，所以AM也是△ABC的角平分线，所以MG=MH．以下过程同证法5，不再赘述．

反思证法5是学生的自然思路，证法6是笔者从学生的自然思路出发探寻到的更优化的方法．学生的自然思路反映学生已有的知识基础和思维经验，同时也是学生思维能力提升的出发点和关键点，教师研题、教学时必须予以重视．

3 问题拓展

基于“解题思维异构”视角，通过对原题的进一步探究，经历观察、猜想、验证、证明等数学活动，可以发展学生的推理能力，获取基本活动经验，提高分析问题、解决问题的能力．所以笔者尝试对原题进行拓展研究．

3.1 原题结论衍生

拓展1沿着原题继续思考，可得以下结论：(1)如图8，∠DME始终是120°；(2)△EBM绕着点M顺时针旋转120°可以与△DPM重合；(3)△EGM绕着点M顺时针旋转120°可以与△DHM重合；(4)BE=BM+DA．

上述结论是相互关联的，感兴趣的读者可自行探究．任一结论可以变换成原题的结论，形成新的试题．

3.2 改变点D位置的变式

拓展2点D为线段AC上一点．

为确保拓展的正确性，笔者采用“几何画板”模拟几何构图，发现当点D为线段AC上一点时，因为点D和E位置的不确定性，存在图9中的多种情况．

笔者在拓展初始画了草图，由于不够精准，只发现点E存在三种位置，忽略了图9(1)、图9(3)、图9(5)中点E均存在两种位置以及图9(4)中点D,E的特殊情况．笔者感悟到虽然草图能够帮助我们快速理解题意，但有时在画图过程中不注意数量关系、位置关系，求解会出现遗漏．因此精准作图就显得尤为重要，借助几何直观能够帮助我们在理解问题的基础上发现其中特殊的数量关系或位置关系．[4]

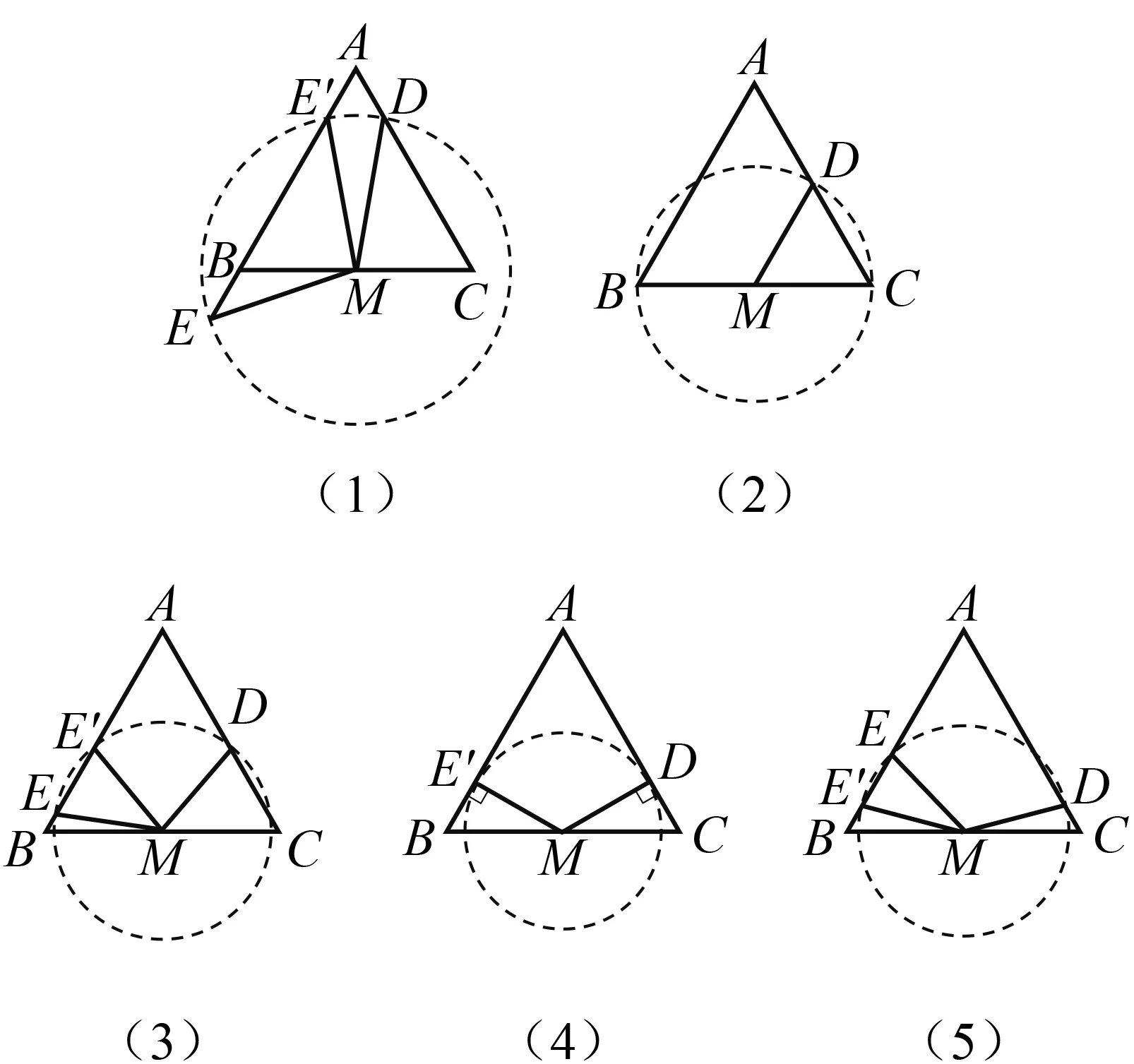
图9

为了对接图1，也因为图9(3)与图9(5)非常相似，所以笔者选择研究图9(1)、图9(5)中的两种点D,E的情况，将原题改编为问题1、问题2．

问题1如图10，在等边三角形ABC中，点M为边BC的中点，点D为线段AC上一点，点E为线段AB延长线上一点．若MD=ME，N为射线MD与射线BA的交点，探索∠BNM与∠BME的数量关系．

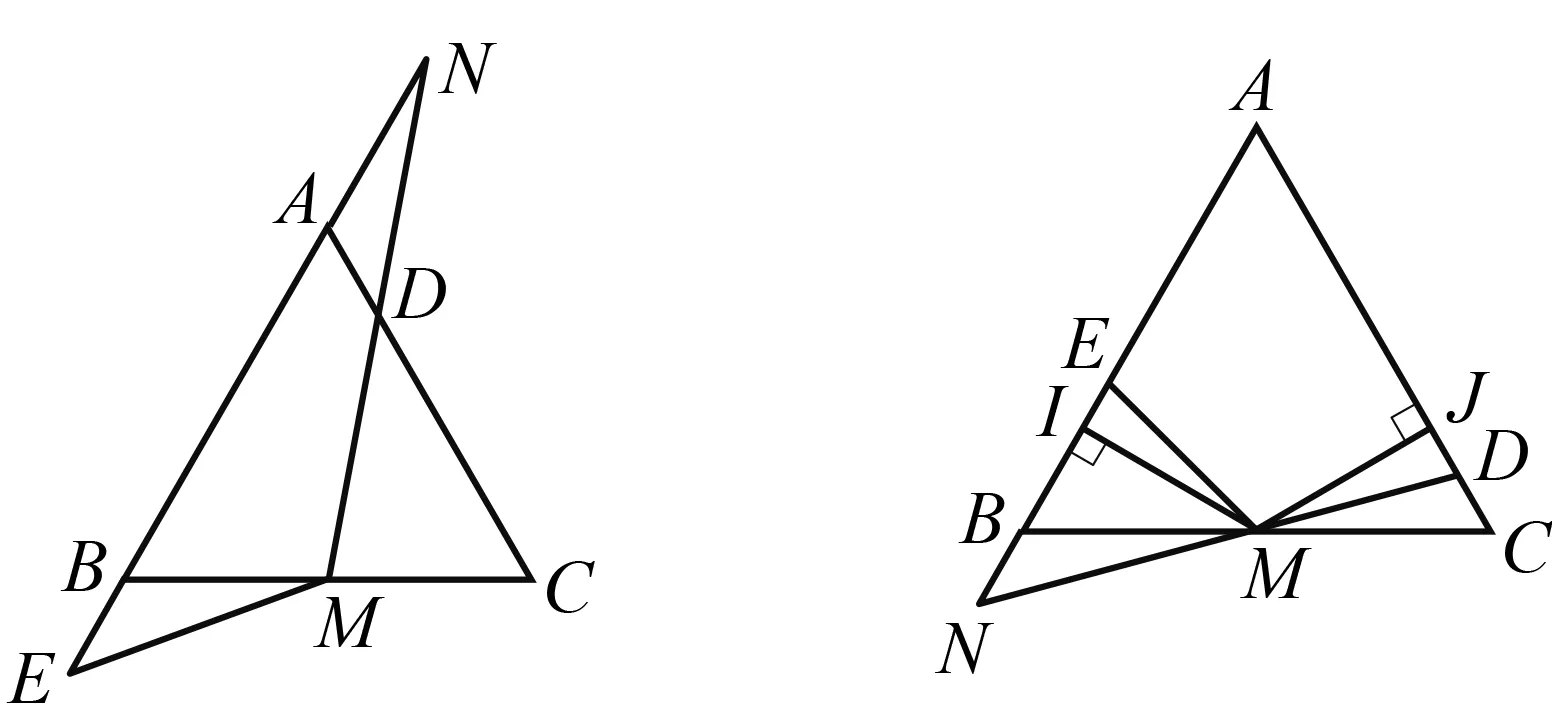
图10 图11

问题2如图11，在等边三角形ABC中，点M为边BC的中点，点D为线段AC上一点，点E为线段AB上一点．过M分别作MI⊥BE,MJ⊥AD，垂足分别为点I,J．若MD=ME，N为射线DM与射线AB的交点，探索∠BNM与∠BME的数量关系．

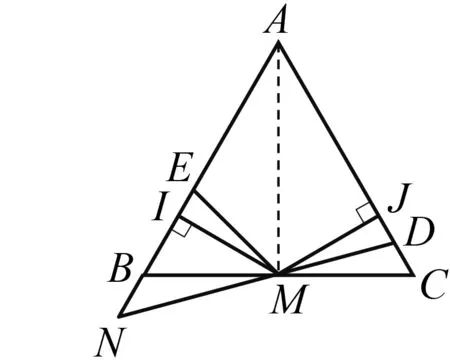
图12

分析 篇幅有限，仅以问题2为例探究．如图12，在图11的基础上连结AM，同理可证MI=MJ．因为MD=ME，所以Rt△MIE≌Rt△MJD(HL)，故∠IEM=∠JDM．因为∠BNM=180°-∠BAC-∠JDM，∠BME=180°-∠ABC-∠IEM，所以∠BNM=∠BME．也可以证明∠BME=∠BMI+∠IME=30°+∠IME=30°+∠DMJ=30°+∠JMC-∠DMC=30°+30°-∠DMC=60°-∠DMC，∠BNM=∠ABC-∠BMN=60°-∠DMC，得到∠BNM=∠BME．其他方法从略．

图10可以参考此证法探究，易证∠BNM=∠BME．

感兴趣的读者可以仿照问题1、问题2为图9的其余图形情况编制问题，注意表述准确严谨即可．

笔者研究发现，当点D为线段AC上一点，点E为图9(1)中点E、图9(3)中点E、图9(4)中点E′、图9(5)中点E时，∠BNM与∠BME的数量关系是∠BNM=∠BME．当点D为线段AC上一点，点E为图9(1)中点E′、图9(3)中点E′时，∠BNM与∠BME的数量关系是∠BME′-∠BNM=60°．当点D为线段AC上一点，点E为图9(5)中点E′时，∠BNM与∠BME的数量关系是∠BNM+∠BME′=60°．

拓展3点D为线段AC延长线上一点．

为确保拓展的正确性，笔者同样采用几何画板模拟几何构图，发现当点D为线段AC延长线上一点时，同样因为点D,E位置不确定，存在 图13中的多种情况．

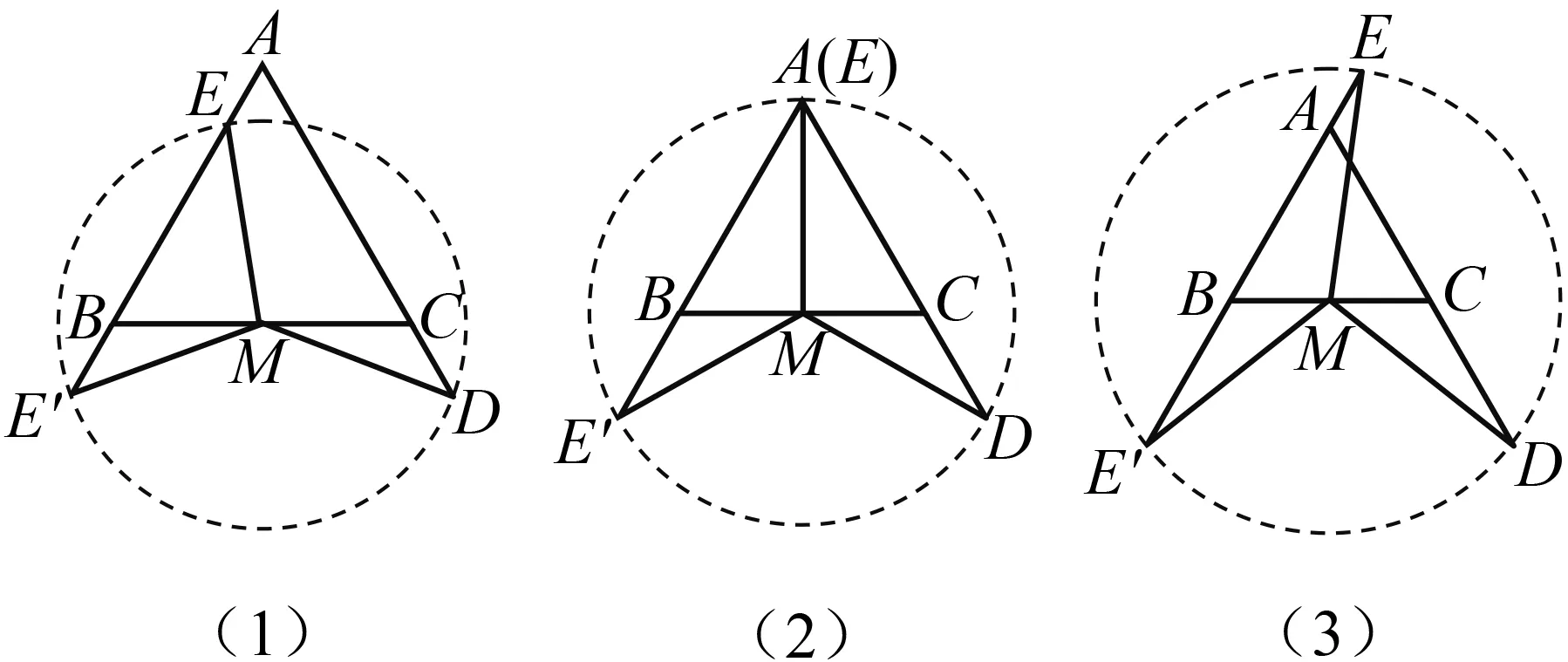
图13

笔者选择研究图13(1)、图13(3)中的两种点D,E的情况,将原题改编为问题3、问题4．

问题3如图14，在等边三角形ABC中，点M为边BC的中点，点D为线段AC延长线上一点，点E为线段AB上一点．若MD=ME，N为射线DM与线段AB的交点，探索∠BNM与∠BME的数量关系．

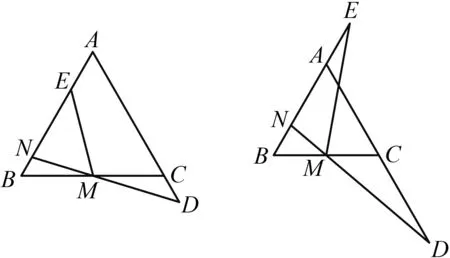
图14 图15

问题4如图15，在等边三角形ABC中，点M为边BC的中点，点D为线段AC延长线上一点，点E为线段BA延长线上一点．若MD=ME，N为射线DM与线段AB的交点，探索∠BNM与∠BME的数量关系．

分析 观察图14、图15发现，无论点E在线段AB上或者线段AB延长线上，点N均在线段AB上．所以图14、图15可以化成一种情况研究．类比问题2的证法，同理可得∠BNM与∠BME的数量关系是∠BNM+∠BME=180°．

笔者研究发现，当点D为线段AC延长线上一点，点E为图13(1)中点E′、图13(3)中点E′时，∠BNM与∠BME的数量关系是∠BNM+∠BME′=120°．当点D为线段AC延长线上一点，点E为图13(2)中点E时，∠BNM与∠BME的数量关系是∠BNM=∠BME=90°．当点D为线段AC延长线上一点，点E为图13(2)中点E′时，∠BNM=90°，∠BME′=30°．

反思如果把原题中“点D为线段AC上一点”变成“点D为直线AC上一点”，因为点D与E位置不确定，就需要分类讨论．点D可以在线段AC、线段CA延长线、线段AC延长线上，这样就把问题转化为原题、问题1、问题2、问题3、问题4等，就会出现很多种图形情况，综合得到∠BNM与∠BME不同的数量关系．分类讨论是一种重要的数学思想方法，分类讨论的过程就是对问题共性的抽象过程，也是一种归纳推理．学会分类讨论，多角度思考问题，有利于分析问题、解决问题．

3.3 改变△ABC形状变式

拓展4从等边三角形到等腰直角三角形．

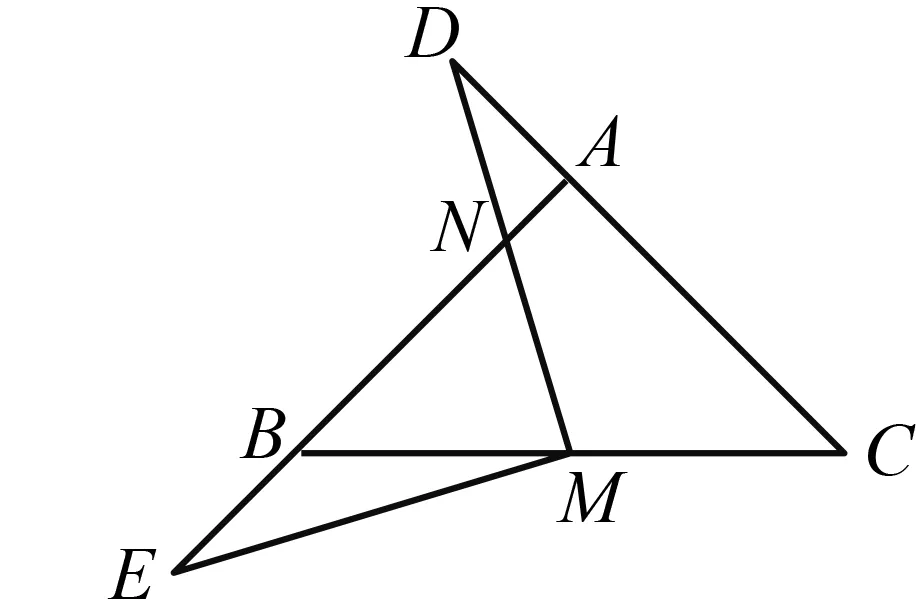
图16

如图16，在△ABC中，AB=AC，∠BAC=90°，点M为边BC的中点，点D,E分别为CA,AB延长线上的一点．若MD=ME，N为线段MD与线段AB的交点，探索∠BNM与∠BME的数量关系．

分析 连结AM，过M分别作AB,AC的垂线段．类似地，探究可证得∠D=∠E，从而得到∠BNM=∠BME+45°．继续研究，可以得出∠DME始终是90°．

笔者马上发现，图16来源于苏科版教材八年级下册第95页22题：如图17，在正方形ABCD中，对角线AC,BD相交于点O，正方形A′B′C′D′的顶点A′与点O重合．图中这两个正方形重合部分的面积是正方形ABCD面积的几分之几？如图18，在正方形A′B′C′D′绕点A′旋转的过程中，这两个正方形重合部分的面积会发生变化吗？证明你的结论．

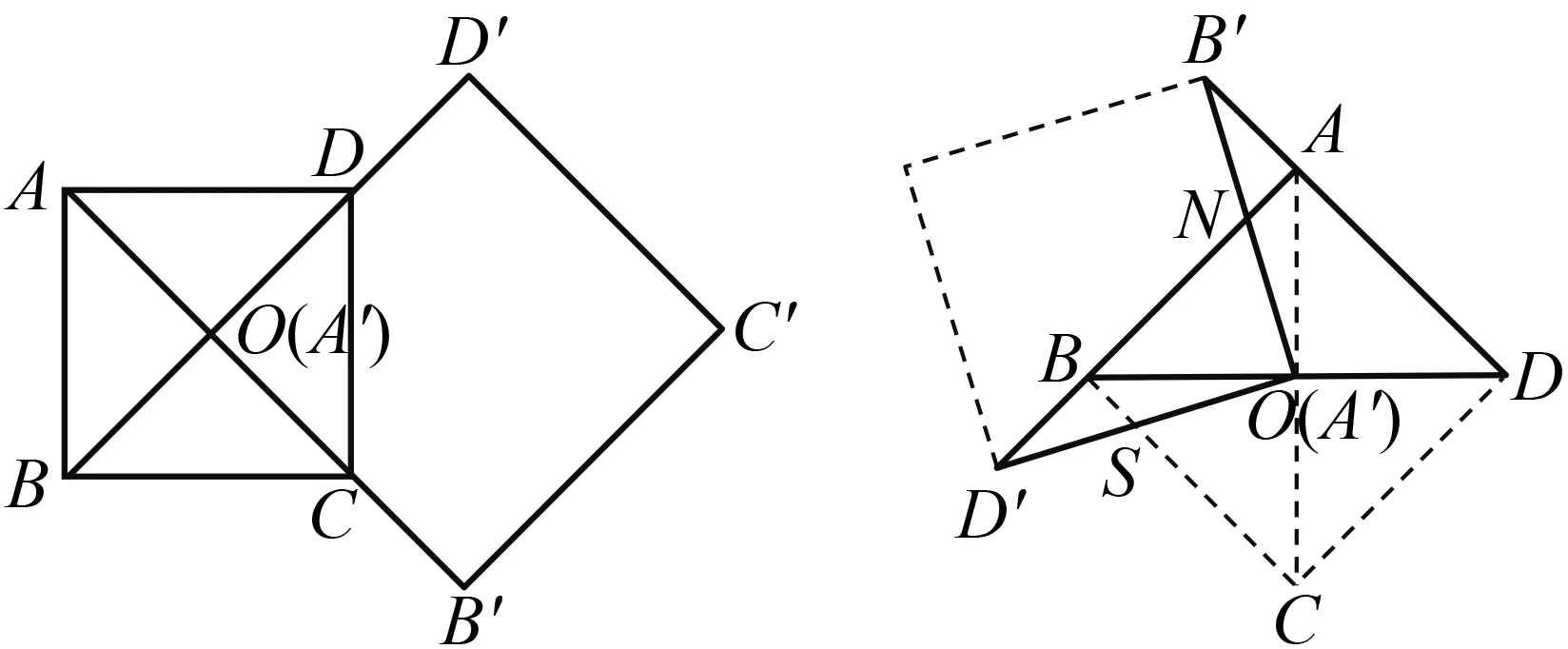
图17 图18

上述问题常用的辅助线作法是过点O作AB,BC的垂线段.笔者逐渐接近拓展4及竞赛题的本质，相当于挖出题目之根，同时也更加理解证法探究中的思维过程．

反思许多中考题、竞赛题都是以教材中的例习题为背景，经过命题者巧妙构思精心打磨而成，在思路方法上具有类比迁移和拓展探索性．教师要熟悉教材、钻研教材，发挥自己的教学智慧，创造性地使用教材．要基于“解题思维异构”视角，充分挖掘例习题所蕴含的数学中的重要思维和思想精髓，通过类比、延伸、迁移、拓展，提出新的问题并加以解决．

解题中，教师不能仅仅“畅游题海”，否则会“苦海无边”;要学会反思，并力求揭示问题的数学本质．溯源问题的本质，正是一种对数学“真”与“美”的追求．

拓展5从等边三角形到普通等腰三角形．

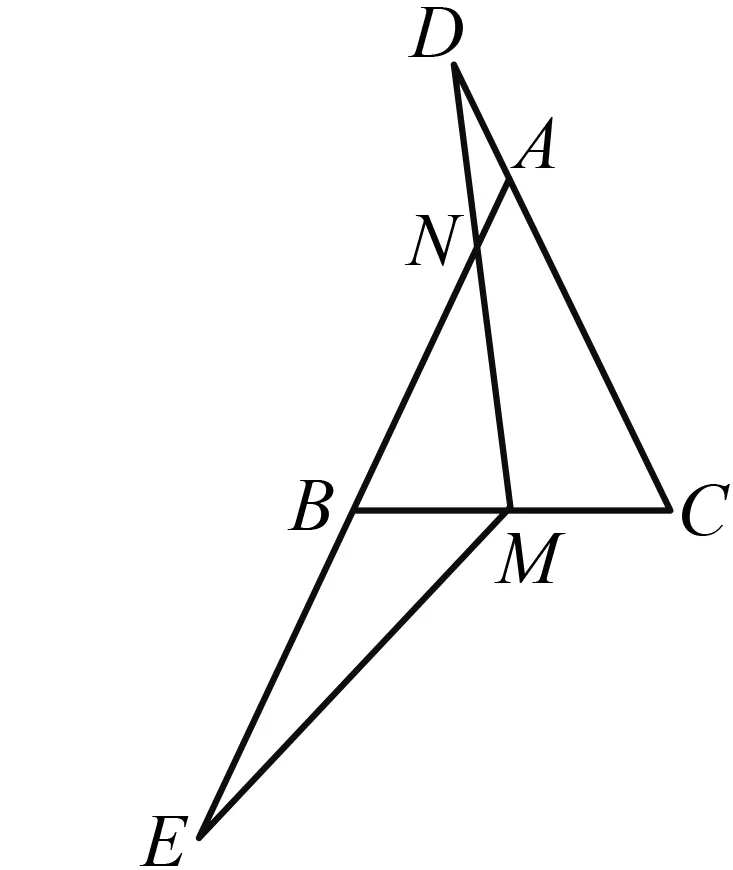
图19

如图19，在△ABC中，AB=AC，点M为边BC的中点，点D,E分别为CA,AB延长线上的一点．若MD=ME，N为线段MD与线段AB的交点,探索∠BNM与∠BME的数量关系．

分析 虽然△ABC从等边三角形变为以∠A为顶角的普通等腰三角形，但AM仍然是△ABC的角平分线，所以∠D=∠E仍然成立．因为∠BNM=∠DNA=∠BAC-∠D，∠BME=∠ABC-∠E，所以∠D=∠BAC-∠BNM，∠E=∠ABC-∠BME，故∠BAC-∠BNM=∠ABC-∠BME，即∠BNM-∠BME=∠BAC-∠ABC．

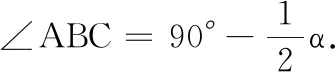
反思通过拓展5的研究，对竞赛题及拓展题的结论进行了抽象归纳，形成了问题的一般性结论．笔者更深入地感悟到竞赛题本质，形成了“探究角之间数量关系”的基本经验．拓展中，无论是点D位置的改变还是△ABC形状的改变，无不渗透着由特殊到一般、分类讨论、类比、转化的数学思想方法．章建跃博士说过：“研究对象在变，研究套路不变，思想方法不变，这就是数学基本思想、基本活动经验的力量．”[5]这样的拓展研究有利于教师本身感悟数学基本思想积累数学思维活动经验、发展推理能力，从而提高解决问题的能力，获得解决同一类型问题的基本经验和思路．

4 结语

在“解题思维异构”视角下，通过对这道几何竞赛题的证法探究及多角度、多层次的变式拓展，笔者比较深刻地认识了竞赛题的庐山真面目，提高了解题的信心．同时，由表及里、层层深入、现学现用，真实体验了几何研究的基本思想方法和基本套路，切实获得了数学“变中不变，变中存本”的基本经验．