2020年高考数学江苏卷第20题的反思与推广

钱月凤 (江苏省苏州中学校 215007)

解题是一门实践性的学问，研究解题是为了提高解题能力．本文从2020年江苏高考数学第20题出发，从解题反思的视角，反思了其解题思路、问题表征和思想策略，之后对此高考题进行改编与推广，最后总结了笔者的几点想法．

1 案例呈现

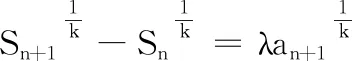
(1)若等差数列{an}是“λ～1”数列，求λ的值；

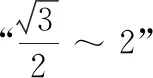
(3)对于给定的λ，是否存在三个不同的数列{an}为“λ～3”数列，且an≥0？若存在，求λ的取值范围；若不存在，说明理由．

解(1)(2)略．

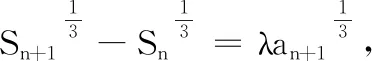
①若λ≤0或λ=1时，则关于cn的方程(*)只有一解cn=1，则符合条件的数列{an}只有一个，此数列为1, 0, 0, 0, …．

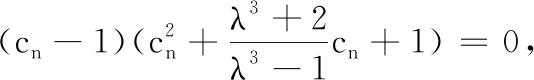
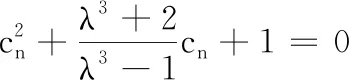
由于数列{Sn}从任何一项求其后一项均有两种不同的结果，所以这样的数列{Sn}就有无数多个，则对应的{an}也有无数多个．

综上所述，当0<λ<1时，存在三个不同的各项非负的数列{an}为“λ～3”数列；当λ≤0或λ≥1时，不存在三个不同的各项非负的数列{an}为“λ～3”数列．

2 解题反思

由于例1第(1)问难度不大，第(2)问与第(3)问的解题思想与方法有共通之处，故将分析的重点放在第(3)问，主要从解题思路、问题表征以及思想策略三方面对解题过程进行反思．

2.1 反思解题结构，实现解题思路明晰化

提炼第(3)问的解题步骤，大致可以分为三大步，记作L1，L2和L3．

第一大步L1：根据“λ～3”数列的定义，将问题转化为方程根的问题．有这样的一个信息流程图(图1)．

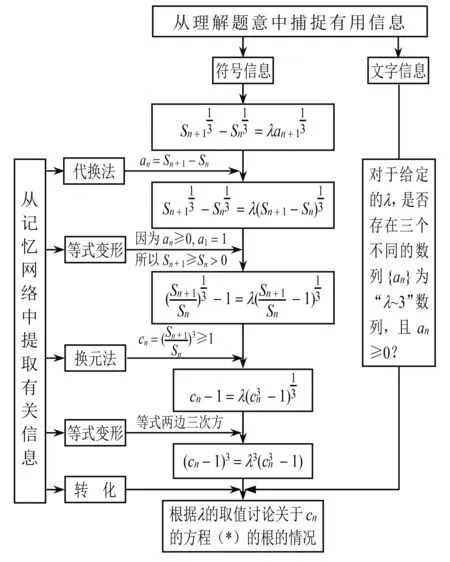
图1 信息流程图

第二大步L2：根据λ的取值来讨论关于cn的方程(*)的根的情况，可分为三类：①λ≤0或λ=1时，方程(*)只有一解cn=1；②λ>1时，方程(*)只有一解cn=1；③0<λ<1时，方程(*)有两个解：一解为1，另一解大于1．

第三大步L3：根据方程(*)根的情况分析数列{Sn}的个数，进而判断满足条件的数列{an}的个数．当λ≤0或λ≥1时，方程(*)只有一解，则符合条件的数列{an}只有一个；当0<λ<1时，数列{Sn}就有无数多个，则对应的{an}也有无数多个，故此时存在三个不同的各项非负的数列{an}为“λ～3”数列．

将整个解题过程分为以上三大步，使复杂问题的求解过程得以清晰地呈现．由以上三大步的结构分析中可以看到，最关键的是第一大步，而第一大步中最有价值的解题进展是“利用换元法将原始问题转化为讨论方程根的情况问题”．

2.2 反思问题表征，力求解题过程自然化

问题表征是解决问题时理解问题的方式．反思问题表征，能加强对问题信息的感知、理解与内化，促进解题主体对解题思路的探求．

问题的呈现方式对策略选择有直接的影响．若问题呈现时省略第(2)问直接跳到第(3)问，很多考生会产生无从下手之感．第(2)问给出后，解题主体会尝试从基础入手，不断探索解题思路，由浅入深，逐渐找到第(3)问的解题突破口，这样便能自然地往下想、往下做．单墫老师曾在《解题研究》一书中提到，所谓自然，即抓住问题的实质，题目该怎么解就怎么解，不顾弄玄虚，朴实自然[1]．

2.3 反思思想策略，促使数学思维深刻化

例1第(3)问所选择的主要解题策略是简化与转化，涉及的主要知识点、数学方法、数学思想和数学能力如表1所示．

表1 例1第(3)问涉及的知识点、 数学方法、数学思想和数学能力

问题涉及的数学知识点不多，但要真正解决该问题，需要解题主体拥有良好的数学思维品质．能否透过问题表面洞察其本质，是数学思维深刻与否的主要表现；全面周密地思考问题，是数学思维严谨性的主要特征．当然，解决该问题还需解题者具备灵活的思维，善于调整解题思路与方法，随机应变．当考生面对问题不知从何下手时，可以静下来想一想：解题的突破口在哪？问题中最重要的条件是哪一个或哪几个？既然我找到了我认为最重要的条件，我该怎么使用它？它想告诉我什么？隐藏在它背后的深刻含义是什么？一旦解题者在思考与探索中找到了突破口，便能选择合适的解题策略，灵活地将基本数学思想与方法运用其中，自然地将陌生难题转化为熟悉的问题．

3 拓展延伸

笔者结合现有经验，对例1进行了更加深入的研究．我们可以将例1中k为大于1的正整数时的所有情形考虑清楚(见例2)．

(1)对于给定的λ和k(k为大于等于3的奇数)，是否存在三个不同的数列{an}为“λ～k”数列，且an≥0？若存在，求λ的取值范围；若不存在，说明理由．

(2)对于给定的λ和k(k为正偶数)，是否存在三个不同的数列{an}为“λ～k”数列，且an≥0？若存在，求λ的取值范围；若不存在，说明理由．

(1)①若λ≤0时，因为k为大于等于3的奇数，所以λk≤0，则关于dn的方程(*)只有一解dn=1，即符合条件的数列{an}只有一个，此数列为1, 0, 0, 0, …．

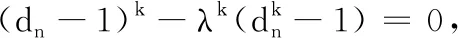
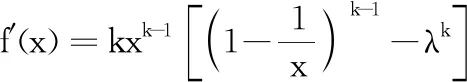
由于数列{Sn}从任何一项求其后一项均有两种不同的结果，所以这样的数列{Sn}就有无数多个，则对应的{an}也有无数多个．

综上所述，当0<λ<1时，存在三个不同的各项非负的数列{an}为“λ～k”数列；当λ≤0或λ≥1时，不存在三个不同的各项非负的数列{an}为“λ～k”数列．

(2)①若λ=0，则关于dn的方程(*)只有一解dn=1，即符合条件的数列{an}只有一个，此数列为1, 0, 0, 0, …．

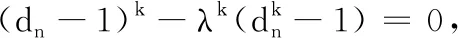
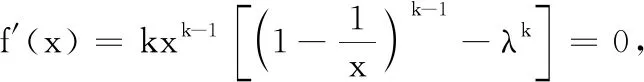
由于数列{Sn}从任何一项求其后一项均有两种不同的结果，所以这样的数列{Sn}就有无数多个，则对应的{an}也有无数多个．

综上所述，当0<λ<1或-1<λ<0时，存在三个不同的各项非负的数列{an}为“λ～k”数列；当λ=0或λ≥1或λ≤-1时，不存在三个不同的各项非负的数列{an}为“λ～k”数列．

现将例2进一步推广，改编成例3；例3具体问题及其求解分析如下：

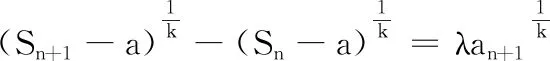
(1)对于给定的a,λ和k(k为大于等于3的奇数)，是否存在三个不同的数列{an}为“a～λ～k”数列，且an≥0？若存在，求λ的取值范围；若不存在，说明理由．

(2)对于给定的a,λ和k(k为正偶数)，是否存在三个不同的数列{an}为“a～λ～k”数列，且an≥0？若存在，求λ的取值范围；若不存在，说明理由．

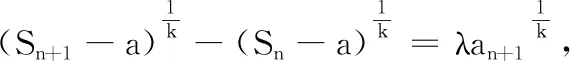
于是，问题转化为根据λ的取值讨论方程(*)的根的问题．之后的求解与例2相同．

答案 (1)当0<λ<1时，存在三个不同的各项非负的数列{an}为“a～λ～k”数列；(2)当0<λ<1或 -1<λ<0时，存在三个不同的各项非负的数列{an}为“a～λ～k”数列．

例3还可进一步推广改编成例4，例4具体问题及其求解分析如下：

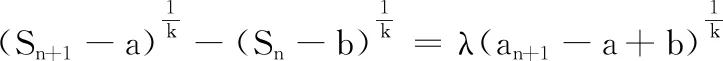
(1)对于给定的a,b,λ和k(k为大于等于3的奇数)，是否存在三个不同的数列{an}为“a～b～λ～k”数列，且an≥|a-b|？若存在，求λ的取值范围；若不存在，说明理由．

(2)对于给定的a,b,λ和k(k为正偶数)，是否存在三个不同的数列{an}为“a～b～λ～k”数列，且an≥|a-b|？若存在，求λ的取值范围；若不存在，说明理由．

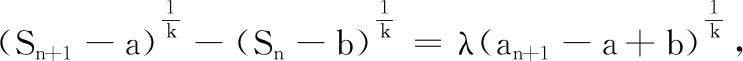
于是，问题转化为根据λ的取值讨论方程(*)的根的问题．之后的求解与例2相同．

答案 (1)当0<λ<1时，存在三个不同的各项非负的数列{an}为“a～b～λ～k”数列；(2)当0<λ<1或-1<λ<0时，存在三个不同的各项非负的数列{an}为“a～b～λ～k”数列．

特别说明的是，例2～例4中k=1时的情形比较简单，而k是分数或无理数时的情况又较为复杂，故以上三题只研究k为大于等于2的正整数时的情形．

4 反思总结

通过解题反思，结合自身经验关于解题总结了以下几点想法：(1)深刻理解题意后，努力寻找解题突破口；(2)掌握基本数学思想与方法，化繁为简，化难为易；(3)大胆探索，跟着直觉往下想、往下做；(4)不断思考，努力产生“新想法”和“新途径”；(5)全面思考问题，创造性地克难攻坚．