基于压力路径法的RC梁受力性能试验研究

熊二刚 祖坤 张倩 谭赐 赵娜娜 丁怡洁

(1.长安大学 建筑工程学院，陕西 西安 710061；2.西安欧亚学院 人居环境学院，陕西 西安 710065; 3.西安建筑科技大学 土木工程学院，陕西 西安 710055)

近年来，国内外学者研究和分析了钢筋混凝土(RC)构件剪切破坏的相关问题，并提出了桁架理论、修正压力场理论、极限平衡理论、塑性理论、压力路径理论及非线性有限元分析方法等理论。由于钢筋混凝土构件的受剪破坏机理相对复杂，特别是混凝土在开裂之后发生的内力重分布，使得上述理论在实际设计计算过程中出现了一些不合理的情况[1- 3]。目前仍缺乏公认的、针对我国实际工程情况的抗剪理论模型和计算方法，亟需提出一套合理、完善的抗剪承载力计算理论[4]。

1988年Kotsovos[5]提出了“压力路径”(Compressive Force Path，CFP)理论，认为：压力通过梁支座与受压区的压力作用点之间的压力路径进行传递；当梁构件处于极限状态时，其受剪机理应从压力路径的角度进行考虑；梁剪切破坏的发生，是由沿压力路径上垂直于裂缝的拉应力不断发展所导致的[6]。Kotsovos[7- 8]还通过改变箍筋布置位置进行了试验，研究了构件的受剪破坏机理和抗剪承载力，发现抗剪性能受箍筋布置位置影响显著，其主要应力作用于压力传递路径上的相关区域，否定了应力由中性轴以下纵筋销栓作用以及骨料咬合作用来承担的传统理论。“压力路径”理论与“拉压杆模型”都应用了结构内的“力流”概念，这一概念能够包容塑性理论下限定理的优美性和简单性，在此概念基础上建立起来的钢筋混凝土梁剪切理论更容易被学者们所接受[9- 10]。

文中基于“压力路径”理论，制作了剪跨比为4.0、3.0、2.5、2.0、1.5、1.0的6组钢筋混凝土试验梁，研究了压力路径法配筋梁在不同剪跨比下的各项力学性能，并与我国现行混凝土结构设计规范[11]配筋梁进行了对比。

1 基于压力路径法的钢筋混凝土梁抗剪设计方法

为了更好地应用压力路径法模型，众多学者对可能导致梁破坏的因素进行了研究，认为钢筋混凝土梁构件的抗剪承载力与剪跨比密切相关[12- 13]，并将破坏类型分为4类[14]，如表1所示。

表1 破坏类型分类Table 1 Classification of failure modes

1)a、d含义如图1所示。

文中仅研究梁的剪切性能，考虑到类型Ⅰ与梁的弯曲破坏性能有关，类型Ⅳ与深梁的破坏性能有关，可能会发生斜压破坏[15]，在实际中应用较少，这里暂不讨论，故选取类型Ⅱ和类型Ⅲ进行研究，取剪跨比为4.0、3.0、2.5、2.0、1.5、1.0进行试验。

1.1 类型Ⅱ的抗剪设计方法

图1为无腹筋钢筋混凝土梁构件压力路径的物理模型，该模型呈现出被受拉钢筋所束缚的“梳”状。该模型中最主要的部分是具有倾斜支腿的混凝土框架，而结构中的“齿”则代表混凝土悬臂梁，它是由加载过程中不断产生的连续倾斜的裂缝分隔而成的。混凝土梁构件受力时的真实形状与该模型横截面的形状相同。CFP理论认为钢筋混凝土梁的抗剪承载力主要是由框架中的粘结力来提供，下部的齿状混凝土对抗剪强度的贡献源于其自身与受拉钢筋之间的粘结力，但贡献较小。

图1 无腹筋混凝土梁压力路径的物理模型

在无腹筋钢筋混凝土梁中，压力路径改变处的应力仅由混凝土来承担，此时混凝土可提供的剪力VⅡ,1为

VⅡ,1=0.5bh0ft

(1)

式中，b为截面宽度，h0为截面有效高度，ft为混凝土抗拉强度。

对于破坏类型Ⅱ，通过在弯剪段水平部分的加载点以及压力路径方向的改变处施加变化较大的内力来平衡应力。当在斜向与水平方向的转角处布置箍筋时，箍筋可改变图1中的梳状模型，同时会增大斜压作用下垂直构件的剪力，平衡梁中产生的剪力。根据圣维南原理，横向拉应力的影响范围约为压力路径方向改变处的两侧h0距离内，因此箍筋的配置范围也规定在距离支座2.5h0位置两侧的2h0范围内，式(2)给出了箍筋面积Asv,Ⅱ1：

Asv,Ⅱ1=Vf/fyv

(2)

式中，Vf为梁能承受的最大剪力，fyv为钢筋的屈服强度。

在压力路径的水平段，为了维持因裂缝粘结破坏以及弯曲破坏而产生的拉应力，也需要配置一定量的箍筋。同时，由于粘结破坏导致的裂缝深度增加，梁体会发生应力重分布现象，如图2所示。在梁构件发生弯曲破坏时，梁体单元压应力区所产生的应力σt为

|σt|=fc/[5(Fc/Vf-1)]

(3)

Fc=σabxr

(4)

σa=fc+5|ft|

(5)

xr=xfc/σa

(6)

式中，fc为混凝土抗压强度，Fc为受压区混凝土合力，σa为受压区混凝土的平均应力，xr为发生内力重分布后截面受压区的高度。

图2 粘结破坏后梁体的应力重分布Fig.2 Stress redistribution of beam after bond failure

由于混凝土的抗拉强度相对较低，在外荷载作用下，当梁构件某点的拉应力达到抗拉强度时，梁腹部会出现弯曲裂缝，弯曲裂缝一旦产生，便会迅速向受压区下边缘延伸扩展，并逐渐趋于稳定。荷载进一步增大，裂缝的分布范围增大，但截面受压区高度变化较小，因此，可采用应变的平截面假定和线弹性弯曲理论[16- 17]来计算梁受压区高度x：

(7)

式中：ρ为纵筋配筋率；n为钢筋与混凝土的弹性模量比，即n=Es/Ec，Es和Ec分别为钢筋和混凝土的弹性模量。

由σt可计算得到单位长度内的水平及垂直力作用，即

TⅡ,2v=σtb/2

(8)

TⅡ,2h=σtx/2

(9)

故类型Ⅱ破坏最终的水平及垂直箍筋用量为

Asv,Ⅱ2v=TⅡ,2v/fyv

(10)

Asv,Ⅱ2h=TⅡ,2h/fyv

(11)

以上公式计算得到的箍筋量均以单位长度为标准，钢筋布置在梁的跨中至压力路径方向的改变处，构造上应符合箍筋间距不超过0.5h0的要求，构造钢筋所能够承受的应力应大于0.5 MPa，所配的抗剪箍筋与构造钢筋的间距均需符合箍筋的最大间距要求。

1.2 类型Ⅲ的抗剪设计方法

对于类型Ⅲ破坏模式，随着荷载增大，混凝土梁在弯剪段逐渐形成斜裂缝。斜裂缝出现后，部分荷载通过受压混凝土传递到支座位置，此时承载力仍然保持在一定值，无显著降低；主斜裂缝形成后，当受拉钢筋发生屈服时，主裂缝尖端区域的中性轴高度减小，受压区内的拉应力逐渐增大，在合力作用下，当受压区混凝土超过极限承载能力时，试件发生破坏。类型Ⅲ破坏发生时，试件裂缝截面上的内力组成如图3所示。

图3 类型Ⅲ破坏裂缝截面上的内力构成Fig.3 Internal forces on crack section for type III failure

假设此时该处箍筋承担所有剪力，且全都达到屈服状态，可得Tsv,Ⅲ=Asv,Ⅲfyv。对受压区混凝土合力作用点取矩，根据弯矩平衡，有

Rfav-Tsv,Ⅲ(av/2)-Fsz=0

(12)

Fsz=MⅢ

(13)

Mf=σabx(h0-x/2)

(14)

式中，Tsv,Ⅲ为箍筋屈服时的合力，Asv,Ⅲ为箍筋面积，Rf为支座处反力，av为集中荷载到支座处的剪跨长度，Fs为纵筋拉力，z为受拉纵筋到受压区合力作用点的距离，VⅢ为剪力，MⅢ为剪切破坏发生时的弯矩，Mf为梁的受弯承载力。

由图3所示平衡关系，根据上述关系式，可推导出箍筋的用量为

Asv,Ⅲ=2(Mf-MⅢ)/(avfyv)

(15)

通过上述计算得到的箍筋应布置在梁的弯剪段，箍筋的构造要求与类型Ⅱ的相同。

1.3 压力路径法与规范抗剪设计计算的比较

CFP理论认为垂直于压力路径上的拉应力是影响梁构件抗剪性能的主要因素，主要体现在垂直于压力路径的拉应力会随着压力路径方向及位置的改变而不断发生变化；混凝土与纵筋之间所发生的粘结破坏也会产生拉应力，同时，构件的有效截面高度随着裂缝的开展而不断减小。这将使得受压区的混凝土压应力不断增大，导致梁中的应力以及破坏模式发生变化。在抗剪机制层面，CFP理论指出，破坏与压力路径区域内的拉应力发展有关，压力呈双折线状传递，骨料咬合作用和纵筋消栓作用并非抗剪机制的主要部分，构件的最终破坏与中性轴上的应力并无关系。约束箍筋在裂缝发展的相关区域对混凝土施加与压力路径相垂直的压应力，从而在临界区域极大地减小了混凝土所承受的拉应力，使压力路径上的混凝土在路径方向的抗压强度得到显著提高，同时也相应地提高了梁构件的抗剪强度。因此CFP理论指出，仅在拉应力出现范围内的局部区域合理布置箍筋就完全可以避免发生剪切破坏，显著提高梁的抗剪强度。

图4展示了构件内压力的传递路径。

C为混凝土受压区合力，T为纵筋拉力，F为箍筋合力， t1、t2为垂直于压力路径上的拉应力作用

我国GB 50010—2010规范中的受弯构件抗剪承载力计算基于极限平衡理论中的塑性机理，其中混凝土抗剪贡献项的计算公式是依据1985年版设计规范中的试验数据通过数理统计拟合分析来建立的，并根据45°桁架模型来计算箍筋的抗剪贡献，没有考虑纵筋消栓作用的积极贡献。为有效避免脆性剪切破坏的发生，分析设计中设置了较高的安全系数。规范中斜截面抗剪承载力的计算公式如式(16)所示，根据该公式计算得到的箍筋按间距s沿构件长度方向均匀布置。

(16)

式中，Vcs为抗剪承载力设计值，αcv为斜截面抗剪承载力系数，βh为截面高度影响系数，Asv为配置在同一截面内各肢箍筋的总截面积，s为沿构件长度方向的箍筋间距。

2 试验概况

2.1 构件设计

试验过程中，依据压力路径法和我国现行规范分别制作了剪跨比为4.0、3.0、2.5、2.0、1.5、1.0的6组试件，每组2根梁；梁总长2 800 mm，净跨2 400 mm，截面尺寸为150 mm×300 mm。文中以剪跨比为1.5的E组试件为例，展示试验梁的钢筋数量及加载位置、配筋位置、钢筋应变片的布置情况，如表2、图5所示。图5仅展示了梁左侧所布钢筋应变片的情况，试验梁的右侧与左侧对称布置。

表2 试件基本参数Table 2 Basic parameters of test specimens

2.2 试验加载与量测方案

依据GB/T 50152—2012《混凝土结构试验方法标准》[18]来确定具体的试验加载方案。通过两点对称的集中力方式进行加载，试验梁的3种不同剪跨比通过改变加载点的位置来调整实现。在试验梁两侧弯剪段的压力路径传递方向上，每间隔50 mm布置相互垂直的混凝土应变片，同时在跨中位置沿梁高方向水平均匀布置3个混凝土应变片，以观测斜裂缝出现的位置，并记录梁体混凝土的应变。为观察试验中的挠度变化，分别在试件跨中、两端支座和加载点处布置了5个测点，量测试验梁在上述位置的位移以及挠度变化，测点的布置位置如图6所示。试验加载装置如图7所示。

图6 试件测点布置图(单位：mm)Fig.6 Layout of measuring points(Unit:mm)

图7 试验加载装置图Fig.7 Experimental loading set-up

在试验开始之前，参照数字图像相关技术[19- 20](Digital Image Correlation，DIC)的量测方法要求，在梁的正表面用记号笔随机无规则地点上尺寸合适的墨点，便于在加载时用照相机对数据点进行实时测量采集。

2.3 材性试验

2.3.1 混凝土材性试验

本试验中采用强度等级为C30的混凝土，依据 GB/T 50081—2019《混凝土物理力学性能试验方法标准》[21]中的技术方案，在浇筑梁试件时预留6个立方体试块(尺寸100 mm×100 mm×100 mm)和9个标准立方体试块(尺寸150 mm×150 mm×150 mm)，在相同条件下与试验梁一起共同养护28 d后，测量预留的混凝土立方体抗压强度。依据GB 50010—2010《混凝土结构设计规范》[11]中所列出的拉压换算关系式(17)、(18)，得到混凝土抗压强度fcu、fc、ft的实测值分别为32.13、24.42、2.66 MPa。

fc=0.76×a2×fcu

(17)

(18)

2.3.2 钢筋材性试验

在制作试验梁时，选取HRB400级和HPB300级两种钢筋分别用作纵筋、架立筋和箍筋，其直径分为6、8、10和22 mm共4种。依据GB/T 228.1—2010《金属材料拉伸试验第1部分：室温试验方法》[22]中测试方案的要求，在进行材性试验的过程中计算相同类型、相同直径的3根钢筋的屈服强度和极限强度的平均值，材性试验所得的强度实测值见表3。

表3 钢筋材性实测结果Table 3 Measured mechanical properties of steels

3 试件破坏过程

各试件的参数虽然不同，但其破坏均经历了开裂、临界裂缝、极限状态3个阶段。随剪跨比不同，试件主要发生弯曲破坏和剪切破坏两种典型破坏形态，试验梁的弯曲效应随着剪跨比增大愈加显著，此时，破坏形态逐渐由弯曲破坏转变为剪切破坏。

3.1 弯曲破坏

以典型试件B组梁为例，由图8可见，按压力路径法配筋的试验梁B- 3.0和按我国规范配筋的试验梁B′- 3.0发生的均是弯曲破坏。在临界斜裂缝阶段之前，试件上裂缝无明显发展。在荷载为15 kN左右时，试验梁B- 3.0和B′- 3.0均在纯弯段出现第一条竖向弯曲裂缝；随着荷载的继续增大，纯弯段原有裂缝出现一定的延伸和扩展，同时出现一些新的裂缝，两根梁的竖向弯曲裂缝逐渐斜向发展；当分别加载至210、195 kN时，两根梁的跨中位置处及沿压力路径方向上的裂缝都十分显著，试件跨中裂缝加宽，发生弯曲破坏，其中梁B- 3.0受压区压碎明显。图8为试验梁裂缝分布图。

图8 B组试验梁最终破坏对比图

利用DIC技术分析得到的裂缝图见图9。

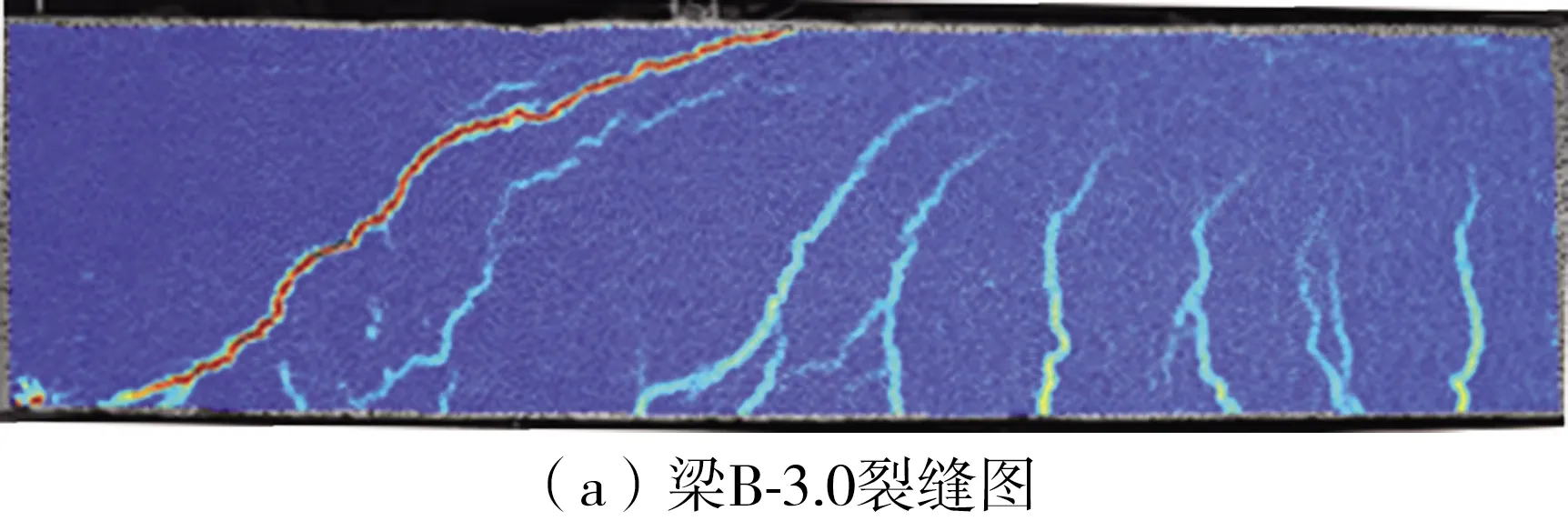
图9 DIC技术所得B组试验梁的裂缝图

3.2 剪切破坏

以典型试件D组梁为例，梁D- 2.0和梁D′- 2.0发生的均是剪切破坏。梁D- 2.0和D′- 2.0的第一条竖向弯曲裂缝出现在纯弯段，此时荷载分别为25和20 kN；继续加载，新的竖向裂缝慢慢在试验梁底部产生，旧裂缝逐渐延伸和扩展，弯剪段出现了第一条腹剪斜裂缝，弯剪段的竖向裂缝开始缓慢斜向发展，后逐渐形成贯通的斜裂缝。当荷载加至310 kN时，梁D- 2.0的斜裂缝加宽，而试验梁D′- 2.0在300 kN时斜裂缝加宽，最终剪压区的混凝土被压碎，承载力丧失，试验梁发生的是剪切破坏。图10给出了D组试件最终破坏的裂缝分布图，图11为运用DIC技术分析得到的裂缝图。

图10 D组试验梁最终破坏对比图

图11 DIC技术所得D组试验梁裂缝图

4 试验结果与分析

4.1 主要试验结果

表4汇总了两种不同方法得到的配筋梁的主要试验结果，对比了各根试验梁的抗剪箍筋面积Asv、开裂荷载Pcr、破坏荷载Pu、梁破坏时加载点处的位移Δu1和跨中位置的最大位移Δu。

根据上述试验结果，在12根试验梁中，压力路径法配筋梁的开裂荷载均低于我国现行规范方法配筋梁的开裂荷载，但开裂荷载之间的差异并不显著；同组试验梁跨中位置处的位移在破坏时相差不大，压力路径法配筋梁在破坏时跨中处的位移均小于规范法配筋梁的位移，但发生斜压破坏的F组梁例外。

表5列出了不同配筋方法试验梁的极限荷载和所节约的配箍量。可以看出：不同组别内两种配筋方法所配箍筋量差异较大，但极限荷载之间的差异并不明显；而且剪跨比越小，根据压力路径法制作的梁所需箍筋量越少。

4.2 抗剪承载力

表6列出了6根压力路径法配筋梁试件的试验结果和试验前的抗剪承载力理论计算值。

从表6可以看出，除F组梁外，试验所得荷载与压力路径法计算的理论极限荷载无明显差异。由压力路径法计算得到的理论值略小于实测值，该结果很好地验证了基于压力路径法进行抗剪设计的科学性及合理性。

表4 试验结果汇总Table 4 Summary of test results

表5 试验梁极限荷载对比Table 5 Comparison of ultimate loads of test beams

表6 抗剪承载力试验值与理论值的对比

对于简支梁承受集中荷载的情况，压力路径法可以较为准确地预测承载力大小，但对剪跨比为1.0的F组梁，应用压力路径法抗剪承载力计算公式计算配筋的准确性并不高，梁的最终破坏是由于混凝土被压碎而产生了斜压破坏。因此，类型Ⅲ的破坏模式不适用于剪跨比为1.0的F组梁的抗剪设计，需要对该破坏类型下的抗剪承载力计算做进一步的分析，修正出更为准确的计算式。

4.3 荷载-挠度分析

图12中对比了各试件的荷载-挠度曲线。

图12 各组试验梁的荷载-挠度曲线Fig.12 Load-deflection curves of specimens

在试验梁加载的全过程中，最初裂缝为细微裂缝，应力主要由混凝土承担，此时的纵筋应力很小；伴随着荷载的逐渐增大，试件在纯弯段和剪弯段出现的细微裂缝渐渐发展为主要裂缝，且承担剪力的对象亦由混凝土逐渐转变为箍筋，梁的挠度不断增大。在荷载逐步增大至极限荷载的过程中，梁体裂缝宽度随之增大，试验梁产生明显的挠度直至破坏。

由图12不同配筋方法配筋试验梁的荷载-挠度曲线可以看出，虽然两种不同方法配筋梁所配的箍筋量差异较大，但试验梁的荷载-挠度曲线的增长规律并没有显著的差异，主要区别在于破坏时所对应的挠度有所不同，但两者相差不大。

4.4 应变分析

4.4.1 纵筋应变

为了研究破坏过程中试件纵筋的应变变化及力学特征，在试件的纵筋上布置一定量的钢筋应变片，应变片具体位置如图5所示。图13给出了12根试验梁的荷载-纵筋应变曲线；表7列出了最大荷载下12根试验梁在各测点位置的钢筋应变，其中ε1为支座处与加载点连线的纵筋应变，ε2为加载点正下方的纵筋应变，ε3为跨中位置的纵筋应变。

图13 各组试验梁的荷载-纵筋应变曲线

从表7可以看出：除发生斜压破坏的F组试验梁外，其余组别试验梁在发生破坏时其加载点下方和跨中位置的纵筋均发生了屈服；压力路径法配筋梁无论发生何种破坏模式，其跨中位置的纵筋应变均小于同组内规范法配筋梁的应变；压力路径法配筋梁加载点下方纵筋的应变更大；发生剪切破坏时，对于6组试验梁中加载点与支座连线处的纵筋应变,规范法配筋梁均小于压力路径法配筋梁，而发生弯曲破坏时恰好相反。

表7 各试验梁在不同测点位置的纵筋最大应变

由图13可以看出：在裂缝出现前，试件上纵筋各测点位置处的应变很小，且增长十分缓慢；但当梁跨中位置开始出现竖向裂缝后，加载点下方以及跨中处的纵筋应变逐渐变大；继续加载，试件弯剪段产生裂缝，箍筋此时开始承受应力作用且应力逐渐向支座位置传递，加载点位置与支座连线处的应变增长速度显著加快。

对于A、B、C这3组发生弯曲破坏的试件，其中A组梁中试件A- 4.0加载点位置的纵筋应变增长比跨中的更快，梁A′- 4.0跨中和加载点下方纵筋的应变有相似的增长规律，应变增长值的不同是因为布置在弯剪段箍筋的位置和间距有一定的差异；B组梁加载点下方以及跨中的纵筋应变变化基本相同，由于弯剪段箍筋位置的不同使得B′- 3.0支座位置和加载点连线处的纵筋应变相对较大；C组试件中，梁C- 2.5的跨中应变增长较梁C′- 2.5的慢，但加载点下方的应变变化相对较快。D、E两组试验梁发生的都是剪切破坏，其荷载-纵筋应变曲线变化规律较为相似，在梁将要达到极限荷载时，两种计算方法配筋梁中加载点与支座连线处的纵筋应变增长相对较快，D′- 2.0试件加载点下方和跨中位置纵筋的应变增长规律一致，但由于在弯剪段内所布箍筋的位置和间距不同，导致梁D′- 2.0和D- 2.0的纵筋应变变化有一定的差别；E组梁加载点下方以及跨中处的纵筋应变变化基本一致，但由于梁E- 1.5弯剪段布置了不同数量的箍筋，使得支座连线处与加载点的纵筋应变略大于梁E′- 1.5。梁F- 1.0发生的是斜压破坏，其加载点下方位置纵筋的应变大于跨中处的应变，且没有屈服，而梁F′- 1.0中跨中处纵筋的应变比加载点下方增长得要快且最终发生屈服。

4.4.2 箍筋应变

如图5所示，在试验梁剪跨区段加载点和支座连线处的箍筋内表面布置若干个钢筋应变片，图14展示了各组梁试件的荷载-箍筋应变关系曲线。

分析图14曲线可知，在开始加载后，试验梁中的箍筋应变很小，部分箍筋甚至出现了受压应力状态，斜裂缝出现前箍筋没有起到很大作用，此时试件所受到的剪力近乎全部由混凝土来承担。当加载至极限荷载的35%左右时，斜裂缝开始出现在剪跨区段内，此时混凝土慢慢退出工作，剪力承担对象逐渐转为斜裂缝相交处的箍筋。剪跨区段内箍筋的应变逐渐增长，靠近加载点处的箍筋应变随着持续加载而逐渐增大，而支座附近箍筋应变无明显变化。箍筋在尚未发生屈服时发挥着限制斜裂缝的开展和延伸的作用，这在一定程度上保证了荷载可以继续增大。同时，箍筋应变和梁的挠度随着试验加载也逐渐增大，这直接导致梁腹部区段的箍筋应力达到最大值而首先发生屈服，随后剪切斜裂缝继续向两侧延伸，生成剪跨段通长的斜裂缝，此时梁上部剪压区的混凝土被压碎，最终梁试件发生破坏。

在图14中，对于A、B、C这3组发生弯曲破坏的试件，其中梁A- 4.0、B- 3.0的箍筋应变相比规范法配筋梁更小，梁C- 2.5的箍筋应变相比规范法配筋梁略大。梁A- 4.0、B- 3.0与规范法配筋梁在抗剪箍筋配置位置上的差异较大，可以看出通过合理地布置箍筋位置，能让箍筋更好地发挥作用，限制混凝土拉应力的增长，提高抗剪承载力；梁C- 2.5与梁C′- 2.5抗剪箍筋配筋段相同，可以看出梁C- 2.5的抗剪箍筋发挥了更大的作用。剪跨比为2.0的D组梁和剪跨比为1.5的E组梁都发生了剪切破坏。压力路径法配筋梁的箍筋应变明显大于规范法配筋梁，箍筋在抑制裂缝发展方面体现了良好的效果；而剪跨比为1.0的F组梁，其破坏模式是斜压破坏，在梁F- 1.0比F′- 1.0的箍筋使用量减少68%的情况下，梁F′- 1.0弯剪段箍筋的应变相对较小，可以看出压力路径法配筋梁F- 1.0中的箍筋利用得更为充分。

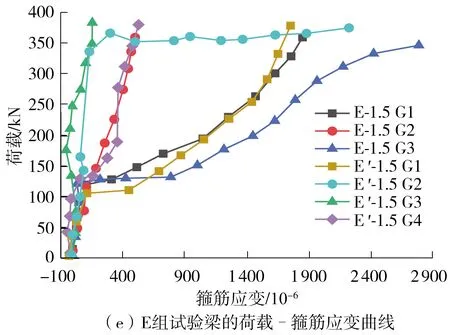
图14 各组试验梁的荷载-箍筋应变曲线Fig.14 Load-stirrup strain curves of test beams

5 结论

(1)通过研究各组试验梁的破坏裂缝分布以及钢筋应力-应变关系曲线的变化，发现压力路径传递方向上的箍筋在抑制斜裂缝发展方面效果显著，这验证了由Kotsovos提出的压力传递路径的合理性，根据压力路径方法进行抗剪设计的梁达到了预期抗剪性能要求；

(2)试验中试件的破坏模式随着剪跨比变化而逐渐转变，剪跨比为4.0、3.0、2.5的梁发生的是弯曲破坏，剪跨比为2.0、1.5的梁发生的则是剪切破坏，剪跨比为1.0的梁发生的是斜压破坏；

(3)对于剪跨比为4.0、3.0、2.5、2.0和1.5的梁试件，应用压力路径法能够较好地预测其极限荷载，但对于剪跨比为1.0的发生斜压破坏的F组梁，根据类型Ⅲ的破坏模式进行抗剪设计配筋则会产生一定的偏差；

(4)在比现行规范所配箍筋减少6%～68%的情况下，压力路径法配筋的试验梁的抗剪承载力没有明显降低，甚至还有提高，这说明压力路径法与我国现行规范设计方法相比，在抗剪设计上展现出了很好的经济性，同时又满足了安全性要求。