原状土的抗剪强度研究

蔡 建

（1.中交上海航道勘察设计研究院有限公司，上海 200120；2.上海航源港口工程质量检测有限公司，上海 200120）

1 引 言

在天然状态下的现场原位土样受正应力和侧向应力作用，为了获得土的抗剪强度指标须采用钻孔取土进行室内试验，土样经过应力释放的卸载和室内试验的再加载过程，土的室内试验抗剪强度指标与土的现场原位抗剪强度指标必然存在差异。土体的抗剪强度是土力学的重要内容之一，是研究土压力、边坡稳定、地基承载力等问题的基础。抗剪强度出现微小偏差将对岩土工程问题的安全、造价带来较大影响，有必要对原状土抗剪强度指标进行研究。

根据土的现场原位和室内压缩曲线的变化规律，结合土的卸载抗剪强度[1]的计算方法，分析加、卸载时土的抗剪强度的变化规律。推导出土的黏聚力和土的内摩擦角两者之间的相互关系，最后分析得出了考虑前期固结应力对土的抗剪强度影响的原状土抗剪强度的计算方法，采用黄文熙[2]和魏汝龙[3]的文献资料进行了试验验证，理论值与试验值基本一致。

2 土的室内和现场原位压缩曲线

土的室内压缩试验反映了土的孔隙比e与有效固结应力σ′（或用p表示）的对应关系，压缩试验的成果可用e-lgσ′表示，图1为正常固结土的e-lgσ′曲线，土样在A点开始加载沿直线AG变化，假设在G点卸载土样e-lgσ′曲线沿GF方向变化，在F点再加载，土样e-lgσ′曲线沿FG方向变化，当压力大于G点时e-lgσ′曲线沿GH方向变化，类似有HE和HK直线变化。

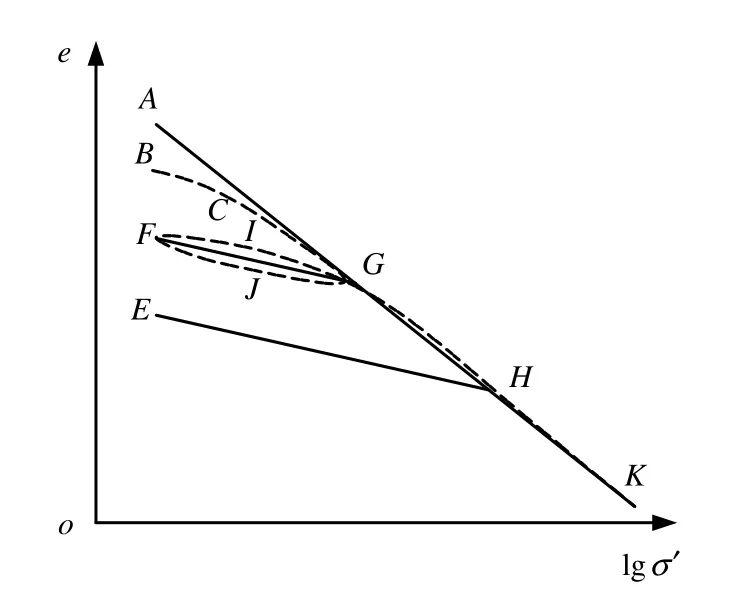
图1 土的压缩曲线Fig.1 Soil compression curve

土样e-lgσ′曲线同样有沿图 1中的加载BCG曲线、卸载GJF曲线、再加载FIG曲线、加载GH曲线方向变化。图1中e-lgσ′曲线有直线和曲线两种表示方法，文献[4－5]指出，图 1中曲线是土的室内压缩曲线，直线是现场原位压缩曲线。

3 土的抗剪强度线

3.1 土的库仑抗剪强度线

法国科学家Coulomb于1776对土进行了一系列试验得到土的加载抗剪强度线，对砂性土和黏性土其抗剪强度的规律可分别采用如下公式描述。

砂性土：

黏性土：

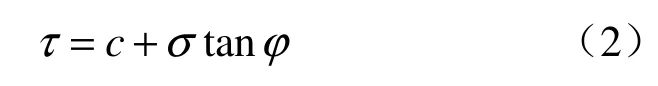
式中：τ为土的抗剪强度；σ为正应力；φ为土的内摩擦角；c为土黏聚力。

土的库仑抗剪强度有以下几点疑问：

（1）文献[5]第260页指出：“……任一平面上的抗剪强度只是该面上法向应力的函数，即

该函数在法向应力与剪应力图上为一曲线，称摩尔破坏包线或摩尔强度线。在一定的应力范围内，这一关系曲线可用线性方程，即库仑定律来表达……”。由此可见，土的抗剪强度线为一段曲线简化成的直线，那么土的抗剪强度线本质上应该是怎样的函数关系曲线？

（2）砂性土黏聚力c=0，黏性土因为含有黏粒，所以具有黏聚力c，为什么具有相同级配、成分和黏粒含量的土具有不同黏聚力值？假如级配、成分和黏粒含量相同的土由于前期固结应力不同，它的黏聚力c值也不同，这不能直观地反映土的前期固结应力对土的抗剪强度的影响，土的库仑抗剪强度定律会不会是一条错误的定律？怎样考虑前期固结应力对抗剪强度的影响？

（3）土的库仑抗剪强度为土的加载抗剪强度线，如果土样在卸载状态时，例如基坑开挖后的坑底卸载土层，真空预压或堆载预压卸除荷载后的土层，此时怎样计算土的抗剪强度？

（4）土的黏聚力和土的内摩擦角两者之间有没有定量关系？假设有，它们的定量关系是什么？

（5）天然土样采用钻孔取土进行室内试验，土样经过应力释放的卸载和室内试验的再加载过程，土的库仑抗剪强度指标为室内强度指标，怎样确定土的现场原位抗剪强度指标？

上述这些问题是值得讨论的。

3.2 土的摩擦抗剪强度线

根据摩擦力公式发生在两相对滑动物体之间的摩擦力f与压力N大小成正比，即

式中：f为摩擦力；N为压力；μ为摩擦系数。

假设土体为正常固结土，从未受到过周围固结压力的饱和正常固结试样不具有强度[5]，此情况下抗剪强度线为通过坐标原点的直线，土的黏聚力为0，初始内摩擦角为φ0，加载固结时土的抗剪强度为

式中：σ′为土的有效应力；φ0为土的初始内摩擦角。

由式（4）、（5）对比可见，经典力学的摩擦力公式对土体材料同样适用。

3.3 土的卸载抗剪强度线

文献[1]根据土的e-lgσ′压缩曲线的变化规律及正常固结土和超固结土的应力关系，得出土的卸载抗剪强度的计算方法，文献[1]中的式（4）可改写为用应力表示的式（6）：

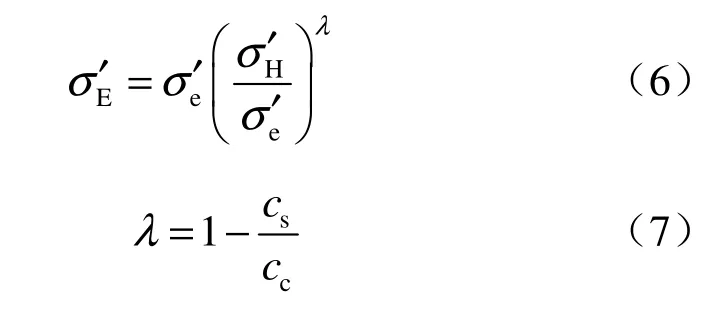
式（6）中各字母含意见文献[7]中图2，假设土体为正常压缩曲线上H点经卸载到E点，土体的最大前期固结应力为，卸载后的土体竖向应力（上覆压力）有两个计算值：一个为不考虑超固结影响土体的竖向应力（上覆压力）；一个为考虑超固结影响土体的竖向应力（上覆压力），换言之，一个土样经过卸载后位于卸载回弹曲线上土体竖向应力（上覆压力），与它具有相同孔隙比所对应的正常压缩曲线上的土体竖向应力（上覆压力）。

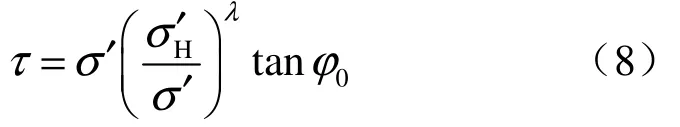
化简后，有

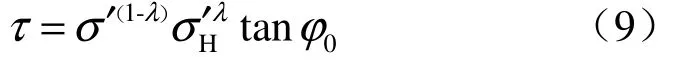
式中：σ′H为土体在固结过程中所受的最大有效固结应力（即图2中H点对应的有效固结正应力）。

式（9）可表示为图2中曲线ODH表示的抗剪强度线，也可简化成图2中的OD和DH直线。

图2 土的卸载抗剪强度线Fig.2 Soil unloading shear strength curve

4 加、卸载时土的抗剪强度变化规律

土的固结过程就是在某一压力作用下有效应力增大、孔隙水压力消散的过程。随着有效应力增大土孔隙比减小，而土的抗剪强度增大，土的压缩曲线与土的抗剪强度线之间有一一对应关系[1,6－7]。

图3的上半部分表示孔隙比e与固结应力的对数值lgσ′的关系，变化过程与图1相同。

图3的下半部分为抗剪强度与有效应力的关系，假设土体沿ah为正常固结土，从未受到过周围固结压力的饱和正常固结试样（土的黏聚力为 0，初始内摩擦角为φ0）土的抗剪强度线为ah，加载到g点后卸载，根据文献[1]沿抗剪强度线gfo曲线变化。再加载先沿ofg变化，荷载超过g点后沿抗剪强度线gh变化到h点。在h点卸载，类似于卸载、加载均重合的oeh抗剪强度线。因为在图3中压缩曲线与抗剪强度线之间有一一对应关系。同样图 2中的ODH可理解为既是加载也是卸载的抗剪强度线。

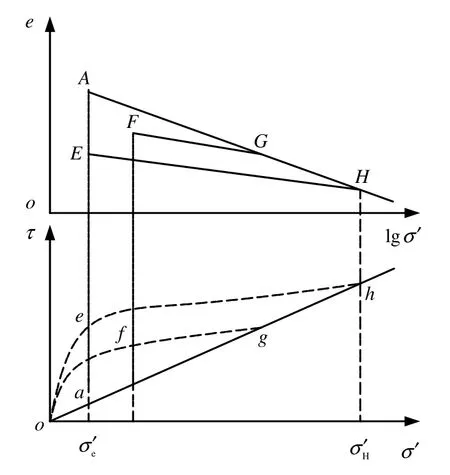
图3 土的抗剪强度的变化规律Fig.3 Variation regularity of soil shear strength curve

5 原状土抗剪强度

5.1 原状土抗剪强度公式

为了与土的库仑抗剪强度相区别，本文采用原状土抗剪强度这一名词表述，原状土抗剪强度线即图2中的OH直线、ODH曲线、HF直线，可用式（10）表示：

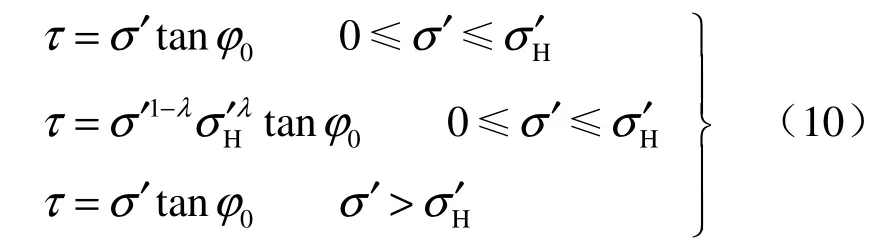
从上面的分析可知，土在初始固结过程中的抗剪强度按式（10）第1式计算。

当土体在某一前期固结应力下已固结时：（1）当有效应力沿大于前期固结应力的方向加载，按式（10）第3式进行土的抗剪强度计算。（2）当土体沿小于前期固结应力的方向卸载，按式（10）第 2式进行土的抗剪强度计算。（3）当土体在小于前期固结应力的情况下沿不大于前期固结应力的方向加载，也按式（10）第2式进行土的抗剪强度计算。

5.2 原状土抗剪强度线的形状研究

在图1中土的压缩曲线为直线，当为砂性土时土的加载压缩和卸载膨胀曲线基本重合，即λ≈0，由式（9）知，原状土抗剪强度线为通过原点的直线，土的黏聚力c≈0。当土中含黏粒时，土的加载压缩和卸载膨胀曲线不重合，λ≠0，由式（9）知，原状土抗剪强度线为图 2中通过原点的ODH幂函数曲线。由于土性系数λ的值不同，原状土抗剪强度线可为直线或曲线，砂性土和黏性土的抗剪强度可采用统一计算公式表示。随着土性系数λ的减小，图2中的ODH幂函数曲线向OH直线变化，当λ=0时，变化成OH直线。

在文献[1]中已研究拐点D点对应的正应力约为前期固结应力的 0.2倍。关于应力较小段OD段曲线是否应该通过坐标原点的问题，笔者认为，如果土的加载压缩和卸载膨胀曲线都是直线，从公式的推导过程看，OD段曲线应为通过坐标原点的幂函数曲线。如果土的加载压缩和卸载膨胀曲线在小应力段不是直线，而是图1中的BCG曲线和GJF曲线，从公式的推导过程看，OD段演变成图4中的不通过坐标原点GD曲线，用GDH曲线表示的抗剪强度线与文献[4，6]黏性土的抗剪强度线一致。因为压缩试验起始压力一般为50 kPa或100 kPa，没有应力较小段加载压缩和卸载膨胀曲线的变化规律，本文不研究图2中OD段抗剪强度线的变化规律，DH段成图2中的CH直线（高校教材中对超固结土小于前期固结压力时土的抗剪强度线也常采用类似CH的直线表示）。图2中的CH直线为小于前期固结应力情况时简化的原状土抗剪强度线。

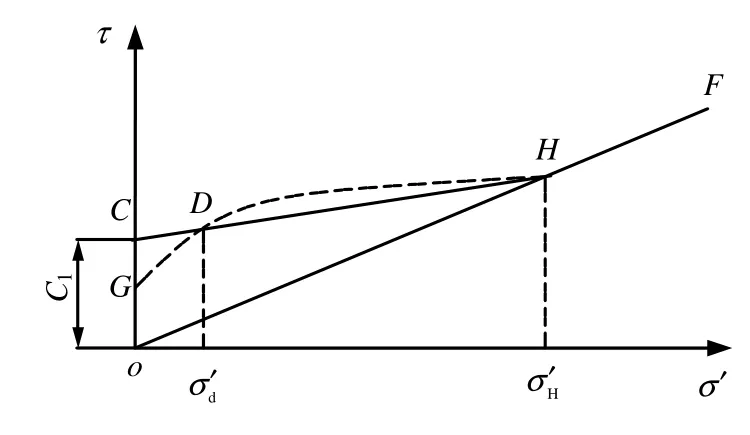
图4 土的抗剪强度线Fig.4 Soil shear strength curve

5.3 土的内摩擦角和土的黏聚力的计算公式

在文献[1]中土的卸载抗剪强度分析中取λ为统计平均值0.64，为具有普遍性现将λ作为一个待定的土性参数进行土的抗剪强度分析，对简化的原状土抗剪强度线CH用c1表示土的黏聚力，k1表示土抗剪强度线的斜率，则土的抗剪强度公式为

简化的原状土抗剪强度指标黏聚力、内摩擦角（或斜率）为

式中：m为系数；φ0为土的初始内摩擦角；φ1为土的内摩擦角（ φ1=arctan(k1)）。

采用文献[1]中的推导方法，经过整理得：

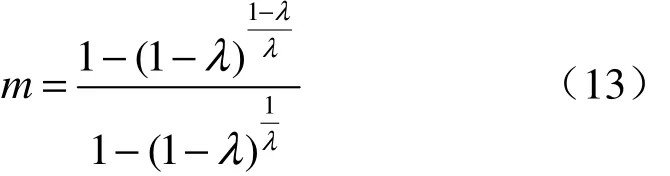
由式（12）可以看出，土的抗剪强度的黏聚力与最大有效固结应力成正比，土的抗剪强度线的斜率（或内摩擦角）为与土性有关的常数。

式（13）表示了m和λ的关系，计算后的m近似值用m′表示，通过拟合计算m和λ关系见图5，式（13）也可近似用式（14）表示。

λ与m值、拟合值m′的关系见表1。

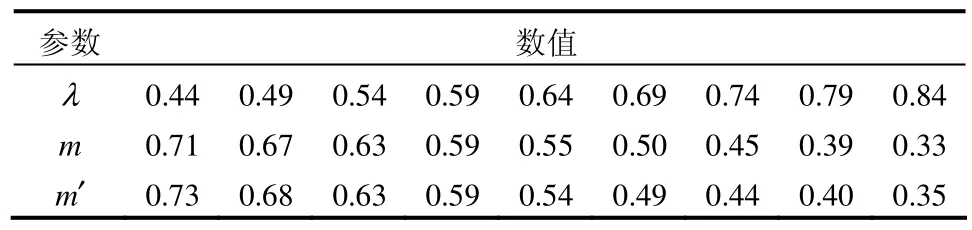
表1 λ与m值、拟合值 m′的关系Table1 Relationships among λ,m,and m′

例如：假设取λ=0.64查表1得m=0.55，再代入式（12）求得c1、k1，再将c1、k1代入式（11），土的抗剪强度便可用下式表示：

5.4 土的黏聚力和内摩擦角之间内在的定量关系

将式（12）化简得式（16），m与土性系数λ有关，可采用式（13）或式（14）计算，也可查表 1得到。

式（16）左边是土的黏聚力和内摩擦角的正切值与前期固结应力之积的比值，右边为关于m的常数，对于某一土样，它的土性参数是惟一的，式（16）揭示了土的库仑抗剪强度的两个指标之间内在的定量关系。

6 土的现场原位测试与室内试验抗剪强度指标的关系

将图2简化成图6，假设现场原位土体为正常固结土，初始抗剪强度线为通过原点的OF线，土样先固结到图6中H点，前期固结应力为H点对应的正应力。

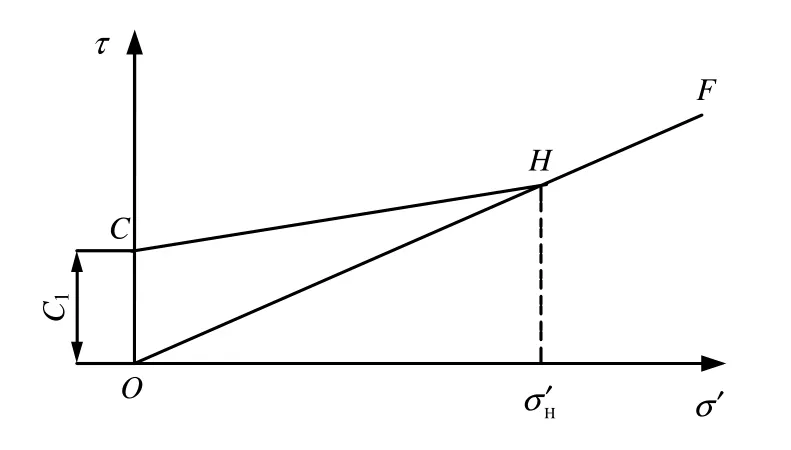
图6 简化的原状土抗剪强度线Fig.6 Simplified intact soil shear strength curve

正常固结土经过现场取土后应力释放接近O点，然后再加载进行室内抗剪强度试验，土的固结抗剪强度线为图中的CH和HF直线组成。假设不考虑土的前期固结应力影响时，室内试验结果是在CH和HF组成的折线上取点，土的库仑抗剪强度指标试验即施加正应力（常规正应力为100、200、300、400 kPa）对应的抗剪强度。比较典型的试验结果可能有以下3种情况：（1）假设土的前期固结应力较大，如某一钻孔的深层土样，试验时施加的正应力均小于前期固结应力，试验结果为CH直线对应的指标；（2）试验时施加的正应力部分点的正应力小于前期固结应力，部分点的正应力大于前期固结应力，在CH和HF组成的折线上取点，试验结果为试验点回归的直线对应的指标，文献[6]指出，这样的结果造成的误差为15%；（3）假设土的前期固结应力较小，如某一钻孔的浅层土样，试验时施加的正应力均大于前期固结应力，试验结果为HF直线对应的指标。

这种室内土的库仑抗剪强度试验结果不一定能反映在工程使用荷载作用下现场原位土体的抗剪强度。土的库仑抗剪强度指标试验最大的缺陷是不能在明确的物理意义和概念下考虑土的前期固结应力对试验结果的影响，然后进行合理、准确的强度试验。

原状土抗剪强度室内试验应根据土样的前期固结应力H点，然后再确定加载、卸载强度曲线CH和加载强度曲线HF，最后根据工程的使用荷载与前期固结应力的关系，在式（10）中选用土的抗剪强度计算公式。

7 原状土抗剪强度与土的库仑抗剪强度的区别和联系

原状土抗剪强度线与土的库仑抗剪强度线的主要区别和联系是：

（1）原状土抗剪强度线揭示了土的抗剪强度线本质上的变化规律是一条幂函数曲线。虽然土的库仑抗剪强度线与原状土抗剪强度线存在误差，但它仍是一条合理的简化直线。

（2）黏性土具有黏聚力主要是由前期固结应力形成的，其值大小基本上与土的前期固结应力成正比，土的库仑抗剪强度定律虽然不能直观地反映前期固结应力对抗剪强度的影响，但由式（12）知，黏聚力的大小已隐含了土的前期固结应力对抗剪强度的影响。

（3）在小于前期固结应力的情况下，土的加、卸载的抗剪强度线重合。此时简化的原状土抗剪强度线与土的库仑抗剪强度线一致，两者均适用于土的加载和卸载抗剪强度计算。

（4）黏聚力和土的内摩擦角的正切值与前期固结应力之积的比值为关于土性系数的常数，揭示了土的库仑抗剪强度的两个指标（土的黏聚力和内摩擦角）之间内在的定量关系。

（5）天然土样采用钻孔取土进行室内试验（同一钻孔中从上到下土样的前期固结应力相差较大），土样经过应力释放的卸载和室内试验的再加载过程后，原状土抗剪强度试验比土的库仑抗剪强度试验方法合理，能根据工程的使用荷载与前期固结应力的关系，选用抗剪强度计算公式，正确考虑了前期固结应力对土的现场原位抗剪强度指标的影响。

8 原状土抗剪强度线验证

8.1 原状土抗剪强度线形状验证

8.1.1 原状土抗剪强度线理论形状

假设取土的初始内摩擦角为28°，土性系数λ为0.64，土样分别在前期固结应力500、800 kPa作用后卸载，计算后原状土抗剪强度线理论形状分别为图7中的OFG和OEH线。

图7 原状土抗剪强度的理论计算曲线Fig.7 Theoretical calculation curve of intact soil shear strength

8.1.2 原状土抗剪强度线试验形状

图8为黄文熙[2]的文献资料中第 292页的图3-74，表示重塑的威尔德黏土各向等压固结不排水强度（有效应力强度）与的关系。和qfm表示前期固结应力和对应的强度（对应于本文中的和τH），和qf为正应力和强度（对应于本文中的σ′和τ），实线AFHK为试验结果。

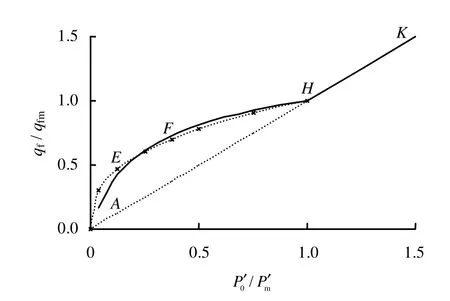
图8 原状土抗剪强度的试验曲线Fig.8 Measured curve of intact soil shear strength

由式（10）的第2式可和式（17）得

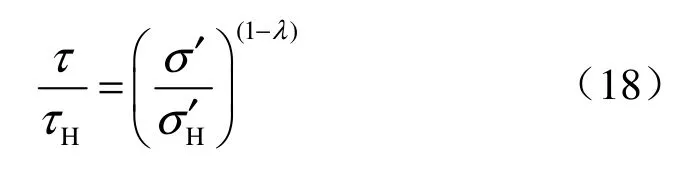
假设取λ=0.64，按式（18）计算得到图 8中OEH虚线表示的土的加载、卸载抗剪强度曲线。由式（10）中的第1式和式（17）得OH虚线表示的初始固结的加载抗剪强线。由式（10）中的第3式和式（17）得HK表示的土的加载抗剪强度线。从图8可以看出，虚线OEH曲线与实线AFH曲线基本重合。因此，式（10）表示的原状土抗剪强度计算公式基本是正确的。

8.2 土的黏聚力和内摩擦角验证

8.2.1 土的黏聚力和内摩擦角之间的定量关系

魏汝龙[3]的文献资料中第 28页对黏聚力c0=0 kPa，土的初始内摩擦角φ0=20°的淤泥质黏土按3种不同的固结压力进行卸载试验，前期固结应力分别为Pcm=100、150、200 kPa，剪切试验时它们的最小正应力分别为25、50、50 kPa，均大于对应前期固结应力的0.2倍，即20、30、40 kPa，不能得出图 2的原状土抗剪强度线ODH曲线，只能拟合成图 6中简化的原状土抗剪强度线CH直线，3条直线见图9，内摩擦角均为12°，黏聚力分别为16、24、32 kPa。

图9为简化的原状土抗剪强度线，将图9中的数值分别代入式（16）计算结果见表2。

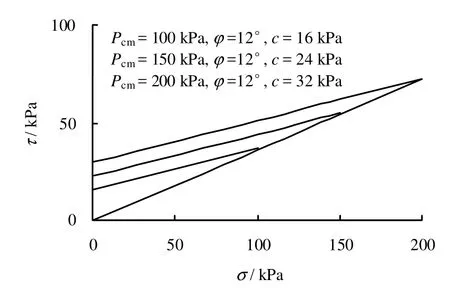
图9 不同前期固结应力时简化的原状土抗剪强度线Fig.9 Simplified intact soil shear strength curves for different pre-consolidation pressures

表2 土的黏聚力和内摩擦角的相互关系Table2 Relationships between cohesion and internal friction angle of soil

从表2知，式（16）右边的比值为0.75，推算出m值为0.57。表2的计算结果表明，黏聚力和内摩擦角的正切值与前期固结应力之积的比值是关于土性系数的常数。

8.2.2 土的黏聚力和土的内摩擦角的理论值计算

同样采用魏汝龙[3]的文献中第28页的资料，假设取λ=0.64，将已知的初始内摩擦角φ0=20°和3种不同的前期固结压力Pcm=100、150、200 kPa分别代入式（12）或式（15）计算土的黏聚力c和内摩擦角φ见表3。

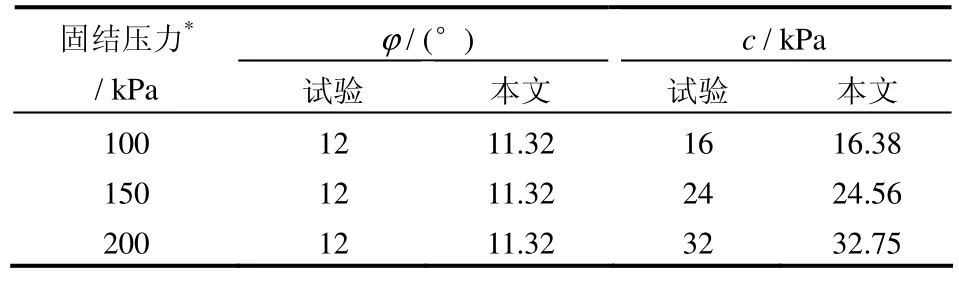
表3 试验结果与本文的计算结果对比表Table3 Comparison between measured value and calculated value according to this paper

从表3可知，式（12）表示简化的原状土抗剪强度指标黏聚力、内摩擦角的计算方法基本是正确的。

9 讨 论

土的库仑抗剪强度指标是1776年库仑（Coulomb）在试验基础上提出的，从公式表面上看，未能反映前期固结应力对土的抗剪强度的影响，是不得以求其次的经验公式，虽然土的库仑抗剪强度定律存在许多缺陷，本文原状土抗剪强度不是对距今已经使用230多年的库仑抗剪强度定律进行全盘否定，而是加深了对库仑抗剪强度定律的理解，补充了土的库仑抗剪强度定律的物理意义，完善了前期固结应力影响下库仑抗剪强度指标的试验方法。砂性土和黏性土的抗剪强度可采用统一计算公式表示，砂性土的抗剪强度线为通过原点的直线，该直线是土性参数λ=0时土的抗剪强度线的特殊情况。

λ是土性参数，不同的土λ值不同，可由室内试验确定，Mayne[3]通过96种黏土试验结果，λ在0.3～1.0之间变化，缺少试验资料时可采用λ的统计平均值0.64。在图8、9中因缺少试验资料，故假设λ=0.64，实测λ的精确值也不一定正好是0.64，λ值可能还应乘以一个修正系数。

本文仅研究了应力历史对原状土的抗剪强度的影响，土的抗剪强度的影响因素很多，其他方面有待土力学爱好者进一步深入研究。

10 结 论

（1）原状土抗剪强度线揭示了土的抗剪强度线本质上的变化规律是一条幂函数曲线与一条直线相连组成。初始固结的加载抗剪强度线为直线，小于前期固结应力的加、卸载抗剪强度线均为幂函数曲线，大于前期固结应力的加载抗剪强度线为直线。

（2）黏性土具有黏聚力主要是由前期固结应力形成的，黏聚力值大小基本上与土的前期固结应力成正比。

（3）在小于前期固结应力的情况下，土的加、卸载的抗剪强度线重合。此时简化的土的抗剪强度线与土的库仑抗剪强度线一致，两者均适用于土的加、卸载抗剪强度计算。

（4）土的库仑抗剪强度的两个指标之间有定量关系，黏聚力和内摩擦角的正切值与前期固结应力之积的比值为关于土性系数的常数。

（5）现场天然土样采用钻孔取土进行室内试验（同一钻孔中从上到下土样的前期固结应力相差较大），土样经过应力释放的卸载和室内试验的再加载过程后，原状土抗剪强度正确考虑了前期固结应力对土的现场原位抗剪强度指标的影响。

[1]蔡建,周健. 土的卸载抗剪强度[J]. 岩土工程学报,2006,28(5): 606－610.CAI Jian,ZHOU Jian. Unloading shear strength of soil[J].Chinese Journal of Geotechnical Engineering,2006,28(5): 606－610.

[2]黄文熙. 土的工程性质[M]. 北京: 水利电力出版社,1983.

[3]魏汝龙. 软黏土的强度和变形[M]. 北京: 人民交通出版社,1987.

[4]殷志建,张诚大,关文光. 土力学与地基基础[M]. 北京: 中国建筑工业出版社,1980.

[5]钱家欢,殷宗泽. 土工原理与计算(第二版)[M]. 北京:中国水利水电出版社,1996.

[6]洪毓康. 土质学与土力学[M]. 北京: 人民交通出版社,1989.

[7]蔡建,蔡继锋. 土的抗剪真强度探索[J]. 岩土工程学报,2011,33(6): 934－939.CAI Jian,CAI Ji-feng. True shear strength of soil[J].Chinese Journal of Geotechnical Engineering,2011,33(6): 934－939.