兼顾系统调压和降损需求的配电网分散式无功控制

钟令枢 管霖

(华南理工大学 电力学院，广东 广州 510640)

以光伏为代表的分布式电源(Distributed Ge-nerators，DG)广泛接入配电网[1]，不仅可以提供廉价、清洁的有功功率，还可以利用逆变器的剩余容量提供无功支持[2]。相比投切电容器、调节有载调压分接头等传统的无功控制方式[3]，直接由高密度部署的DG进行分散无功控制在空间上可以更大限度地减少无功功率传输距离，提高无功补偿的效率；在时间上不受开关动作频次的限制，可以根据系统运行点的变化连续调整补偿量以实现最优无功控制。分布式电源通过智能逆变器参与电压-无功控制已被写入最新的IEEE 1547-2018标准[4]当中，我国的分布式电源并网运行控制规范[5]也要求接入中低压配电网的DG需提供无功控制。

配电网无功控制的主要目的是将负荷节点的电压稳定在规定范围内，并且尽可能地降低系统的有功网损。这一目的可以通过求解一个以分布式电源无功输出为决策变量、以有功网损为优化目标、以负荷节点电压符合要求为约束的最优潮流(Optimal Power Flow，OPF)问题来达成。

由于节点电压、系统网损与所有节点的功率注入均有关，OPF问题的精确求解需要获得全网的量测信息，通常采用集中优化的方式来实现[6- 8]，即设置一个可以获得全网所有节点功率注入的中央控制器，由其计算出每个分布式电源的最优无功输出，再下发到各个DG节点执行。然而，集中计算需要建设一个连接配网中所有节点的实时通信网络，不仅造价高昂，也容易受到通信网络单点故障的影响。此外，集中计算要求配电网中的所有用户提供自己的实时功率需求数据，这些数据中蕴含的个人隐私信息可能被非侵入式负荷监测所提取，恐难以被部分注重隐私的用户所接受[9]。

通过引入一些合理近似，可以将原始的OPF问题转化为半定规划[10- 12]、二阶锥规划[13- 14]等形式较为简单的问题，而后利用配电网自身的拓扑特性将每个DG的最优无功输出表示为部分局部信息的函数，以实现OPF问题的分布式求解[15- 16]。分布式求解方法可以利用很少的通信来达到和集中式优化相近的结果，对于通信网络的单点故障也具有较好的鲁棒性，但在大多数情况下仍需要对所有负荷节点的电压和功率进行测量。微型同步相量测量单元(Micro Synchro Phasor Measurement Unit，μ-PMU)在配电网中的使用为进一步减少对前述隐私信息的依赖提供了新的渠道。以文献[17- 19]为代表的一系列成果通过线性近似，把使得网损最小化的DG最优无功输出表示为邻近DG节点之间的电压相角差的函数，并对DG节点电压约束进行拉格朗日松弛，从而在不收集负荷节点实时功率需求的前提下优化网损，并且保证DG节点的电压满足限值。这种方法在每一个时步的计算中都需要获得邻近DG的相角，故需建立稳定的、能持续通信的信道。此外，持续的通信要求每个时步都留出通信的时间，而电压越限的修复是通过逐步更新对应拉格朗日乘子的反馈控制来实现的，这会导致电压恢复较为缓慢。文献[20]在文献[19]的基础上改用本地电压控制处理DG节点电压约束，提高了电压修复的速度。文献[21]对文献[19]和[20]做了进一步改进，将系统有功网损对DG无功的偏导数表示为DG节点自身电压相角的函数，可以在没有通信的情况下仅凭本地量测优化网损。然而这些方法只能保证DG节点的电压符合要求，并不能保证无法测量的负荷节点的电压也符合要求。此外，文献[19]和[20]理论上能在一个时步内让系统网损达到最小，但需要多个时步的反馈控制才能修复电压越限，而在工程实践中，快速地恢复电压关乎安全，比降低网损等经济性指标更加优先。

为了解决上述问题，在优化网损的同时快速恢复负荷节点的电压，文中对文献[21]的方法做了进一步改进，让DG节点接收周围负荷节点的低电压警报，并根据线路的阻抗参数计算最优的电压支撑策略，以最小的网损代价修复电压越限。文中所述的方法能在一个时步内修复负荷节点的低电压问题，然后逐步优化网损。由于单纯提供越限时的电压幅值信息基本分析不出用电行为，且文中所述的方法对于较大的越限也可在一个时步内修复，无需负荷节点长时间连续提供自身电压信息，因此对用户的隐私友好。

1 基于灵敏度的网损优化问题建模

当系统中所有节点均没有低电压或者过电压风险时，无功控制应以降低系统的有功网损为目标。

为避免电磁环网，配电系统通常以闭环设计，开环运行，实际运行时的网络拓扑为辐射状，可表示为一棵有向树。其中，树的根节点代表与主网连接的系统母线，在分析配电网时视为无穷大母线，下标为0，其电压恒定为VN=1∠0 p.u.。

现考虑一个除根节点外还有m个装有分布式电源的DG节点(以G={G1,G2,…,Gm}标记)及n个纯负荷节点(以L={L1,L2,…,Ln}标记)的辐射状配电系统，系统中的支路以其末端节点的编号标记，例如连接节点i及其父节点的支路标记为支路i。以ei,j表示任意两个节点i和j之间的唯一通路上所有支路的编号构成的集合。为了便于描述系统的拓扑，引入(m+n)×(m+n)维0/1矩阵A，其第i行第j列的元素定义为

(1)

即当且仅当支路i处于连接节点j和根节点的通路e0,j上时，Ai,j不为0。

根据基尔霍夫定律，系统的支路电流可以表示为支路下游节点注入电流之和，节点间电压降可表示为连接两节点的通路上的支路电压降之和：

IBr=AI

(2)

V=1+ATVBr

(3)

1为所有元素均由根节点电压VN=1∠0 p.u.构成的列向量；I为根节点以外的所有节点注入电流构成的列向量，IBr为所有支路电流构成的列向量；V为根节点以外所有节点电压构成的列向量，VBr为所有支路电压降构成的列向量。设支路i的阻抗为zi=ri+ixi，z=r+ix为所有支路阻抗构成的列向量，ri和xi分别为支路i的电阻和电抗，则VBr可表示为节点注入电流的线性函数：

VBr=diag(z)IBr=diag(z)AI

(4)

将式(4)代入式(3)，设H=ATdiag(z)A，则V可表示为I和H的乘积的函数：

V=1+HI

(5)

(6)

(7)

又考虑到同一电网中不同输电线路的阻抗比差值不会过大，使用系统中所有输电线路的平均阻抗角θ来近似地代替每一条输电线路的具体阻抗角，设r0=cosθ，x0=sinθ，z0=r0+ix0，则有

H=|H|z0=|H|r0+i|H|x0

(8)

式(8)中，|H|为H中所有复元素取幅值后得到的方阵。基于上述假设，式(4)可改写成

V=1+(|H|P-i|H|Q)z0

(9)

则式(6)可改写成

PLoss=PT|H|Pr0+QT|H|Qr0

(10)

QLoss=PT|H|Px0+QT|H|Qx0

(11)

将PLoss对Q求导可得灵敏度向量

(12)

式中，Im表示取虚部。将式(12)展开到元素，具体的一个DG节点Gi的无功输出对有功网损的灵敏度可以由本地电压相量算出：

(13)

这一结论在一定程度上是反直觉的，因为网损是一个全局量，网损灵敏度和所有节点的功率注入都有关，却用一个本地量被估计出来了。但如式(12)所示，单一节点的电压相量中确实蕴含着全局信息，可以从中提取出系统所有节点无功注入的加权和，进而计算出节点无功注入对系统总网损的灵敏度，因此式(13)在计算灵敏度时即使只需要本地电压相角，也不会忽略来自其他任何一个节点的影响。

根据式(13)设计控制器，可以在仅跟踪本地电压相量的前提下优化网损：

(14)

(15)

2 以最小网损代价修复负荷低电压的分散式优化方法

当系统中出现电压过高或者过低的节点时，无功控制的目标从降低有功网损转化成了提供电压支撑，以修复负荷节点电压越限。其中，过电压问题在DG节点的逆变器具有足够容量的条件下可以直接用本地电压控制解决，因为负荷节点均为无源的纯负载，系统中的电压最高点一定出现在DG节点或者根节点上，而根节点的电压恒定为1.0 p.u.，只要所有DG节点通过本地电压控制确保电压符合限值，就可以确保系统中所有节点均不会出现过电压。

相比之下，即使所有DG节点电压均符合限值，负荷节点依然可能出现低电压，需要通过DG节点进一步提高无功输出来修复。因此，本节对修复负荷节点低电压的最优无功控制展开讨论。

2.1 消除低电压的最优无功控制问题描述

2ΔQGT|N|QL)r0

(16)

将式(15)代入式(16)，可消去第2和第3项，得

ΔPloss=ΔQGT|M|ΔQGr0

(17)

引入n维列向量ΔVL描述各负荷节点需要抬升的电压，其第j个元素ΔVLj表示负荷节点Lj的电压越限值，当VLj>Vmin时ΔVLj=0，否则ΔVLj=VLj-Vmin。根据上述定义，DG节点的最优无功控制可以表示为一个线性约束的二次规划问题的解：

(18)

s.t. |N|TΔQGx0≥ΔVL。

2.2 基于对偶分解的分散无功控制

(19)

(20)

(21)

(22)

由于式(22)中的矩阵|M|-1|N|具有稀疏性[19]，仅当DG节点Gi和负荷节点Lj之间的通路eGi,Lj上不存在其他DG节点时，[|M|-1|N|]i,j≠0，此时称Gi与Lj“相邻”。根据这一性质，当一个负荷出现低电压时，只有与其最邻近的少数DG节点需要调节无功。因此式(22)可以改写为

(23)

(24)

式中，VLj(ΔQG)为各分布式电源的调节量是ΔQG时节点Lj的电压，可以在调压后直接测量Lj的电压获得。

利用式(23)和(24)，优化问题(18)可以用如下的对偶分解法求解——在每个时步的无功控制中，各个分布式电源Gi按以下两个步骤依次更新拉格朗日乘子和本地无功输出：

(25)

式中，β为常系数。

利用这一策略，各个DG节点只需要获取周边负荷节点利用短距离信道广播的低电压告警，即可在若干次调节无功之后实现最优无功控制。

2.3 无需迭代的分散无功控制

2.2节中提出的基于对偶分解的无功控制方法需要一定次数的迭代才能完成节点电压的修复，在此期间需要DG节点在接到周边负荷节点的低电压警报之后持续监测越限的电压，直至低电压警报解除，这意味着更长时间的稳定通信要求和更长时间的低电压风险。如果能在收到低电压警报之后直接求出修复电压越限所需的调节量，进行一步到位的调节，不仅可以减少电压过低的时间，也可以避免对信道的长时间占用。

由于式(18)在数学上不存在直接获得解析解的方法，需要结合电网的实际特点对其进行进一步简化。

首先考虑只有一个负荷节点Lj出现电压过低的情况，此时最优无功的表达式为

(26)

式中，|N|:,j为矩阵|N|的第j列。此时的电压约束为

(|N|:,j)TΔQGx0≥ΔVLj

(27)

(28)

将式(23)代入式(26)，对于所有与Lj相邻的DG节点Gi，有

(29)

由于式(29)只和Lj需要提升的电压有关，可以直接根据式(29)计算出最优无功调节量。

配电系统出现低电压往往有一个渐进的过程，在最开始的时候只有电压最低的节点出现低电压，随着负荷的持续增加，低电压节点的数量才逐渐增加。如果每一个节点在出现低电压之后都能根据式(29)立即修复，系统可以持续满足电压约束。

当系统中确实存在多个低电压的负荷节点时，可以分别按照单一负荷节点出现低电压的情况计算需要输出的无功，然后选择其中的最大值：

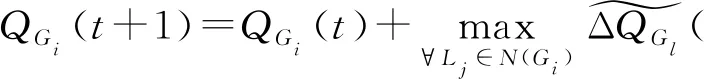
(30)

3 考虑节点电压及配电系统网损的分散无功控制

利用前两节提出的优化技术，结合本地电压控制，可以建立一个兼顾节点电压和有功网损的分散无功控制系统。文中选用的本地电压控制的控制律如下：

QGi(t+1)=QGi(t)+γ(1-|VGi|)

(31)

式中，QGi为自身电压越限的DG节点的无功输出，常数γ为控制器增益。

该无功控制系统要求所有DG节点装有μ-PMU，可以实时测得自身的电压相角；要求无DG的负荷节点能监测自身电压，并在低电压时能向相邻的DG节点发送自己的电压越限量，除此之外无需传送任何隐私信息；另外，要求每个DG具有足够的无功调节能力。满足上述条件后，任何DG节点Gi在时刻t的无功输出QGi(t)可以用图1所示的步骤算出。在这个策略下，各个分布式电源优先保证自身电压处于安全范围，然后尝试恢复邻域内出现低电压的负荷节点。当自身电压符合限值、邻域内也没有需要提供电压支撑的负荷节点时，则尝试优化网损。

图1 考虑负荷电压和系统有功网损的无功控制策略

由于每个分布式电源仅需要保证其邻域内的负荷节点电压符合约束，且各个分布式电源之间不需要相互通信，上述控制方法属于分散式控制的范畴，即使在规模较大的配电系统中，各个分布式电源仅需搜集有限范围内的量测数据即可完成控制任务。相比集中式控制，这种分散式的架构对通信基础设施的要求低得多，因为实时地集中优化网损需要在集中式控制器和各DG之间维持稳定的双向实时信道，为了避免单点故障可能还需要冗余的信道，而文中方法只需要能在出现电压问题时暂时使用的信道，且只需要进行短距离通信。负荷节点向周边的分布式电源广播自己的电压时可以通过载波通信来实现，也可以通过短距离的无线通信来实现，具有更高的现实可行性。在计算上，集中式方法如果要获得比文中方法更优的网损，需要使用基于精确配网模型的非线性优化器，实时计算需要很大的计算资源，且对降损能力的提升极其有限；而文中方法只需要进行矩阵乘法，可以轻易地实现实时性。

4 算例分析

使用改进的IEEE 33节点系统[22]对文中方法的有效性进行验证。网络拓扑和DG装设的位置如图2所示，其中白色节点为纯负荷节点，黑色节点为DG节点。由于文中侧重考虑低电压时的场景，且DG有功波动对式(14)控制效果的影响在文献[21]中已经充分讨论，故这里假设每个DG节点恒定提供275 kW的有功功率，并且有足够的逆变器剩余容量提供无功调节。其余负载在默认值的基础上逐渐增加，以模拟低电压场景。和文献[19- 21]相同，文中的数值仿真采用Matpower进行，每隔1 s更新1次负荷数值，并由图1所述的控制策略计算1次最优无功输出。虽然这里的控制时间间隔设为了1 s，但实际使用中可以根据具体的通信延时酌情增加或减少。作为对比，还设置了2个对照组，其中一个采用文献[19]所述的分布式反馈控制进行无功控制，另一个采用可以获得全局最优解的集中式控制。

图2 改进的33节点系统拓扑和DG装设位置

4.1 负荷逐渐增加时的无功控制效果

首先考虑较为常见的情况，即负荷在平稳运行一段时间后逐渐增加，直至出现低电压。系统先在原始负载下运行50 s，之后在25 s内匀速增加到1.5倍原始负载，并保持25 s。

如图3所示，如果所有分布式电源的功率因数都定为1.0而不提供无功补偿，系统中的低电压问题会随着负载上升逐渐加重。即使采用文献[19]中的分布式无功控制，在负载最重时依然会出现10 s左右的低电压问题。如果使用文中策略进行无功控制，则所有负荷的电压都能持续保持在限值以内。从图4可以看出，在负荷增加的最后10 s内，文中方法大幅提升了29号节点的无功输出，从而将系统末端的电压刚好保持在限值之上。

图3 负荷匀速增加时的全网最低电压变化曲线

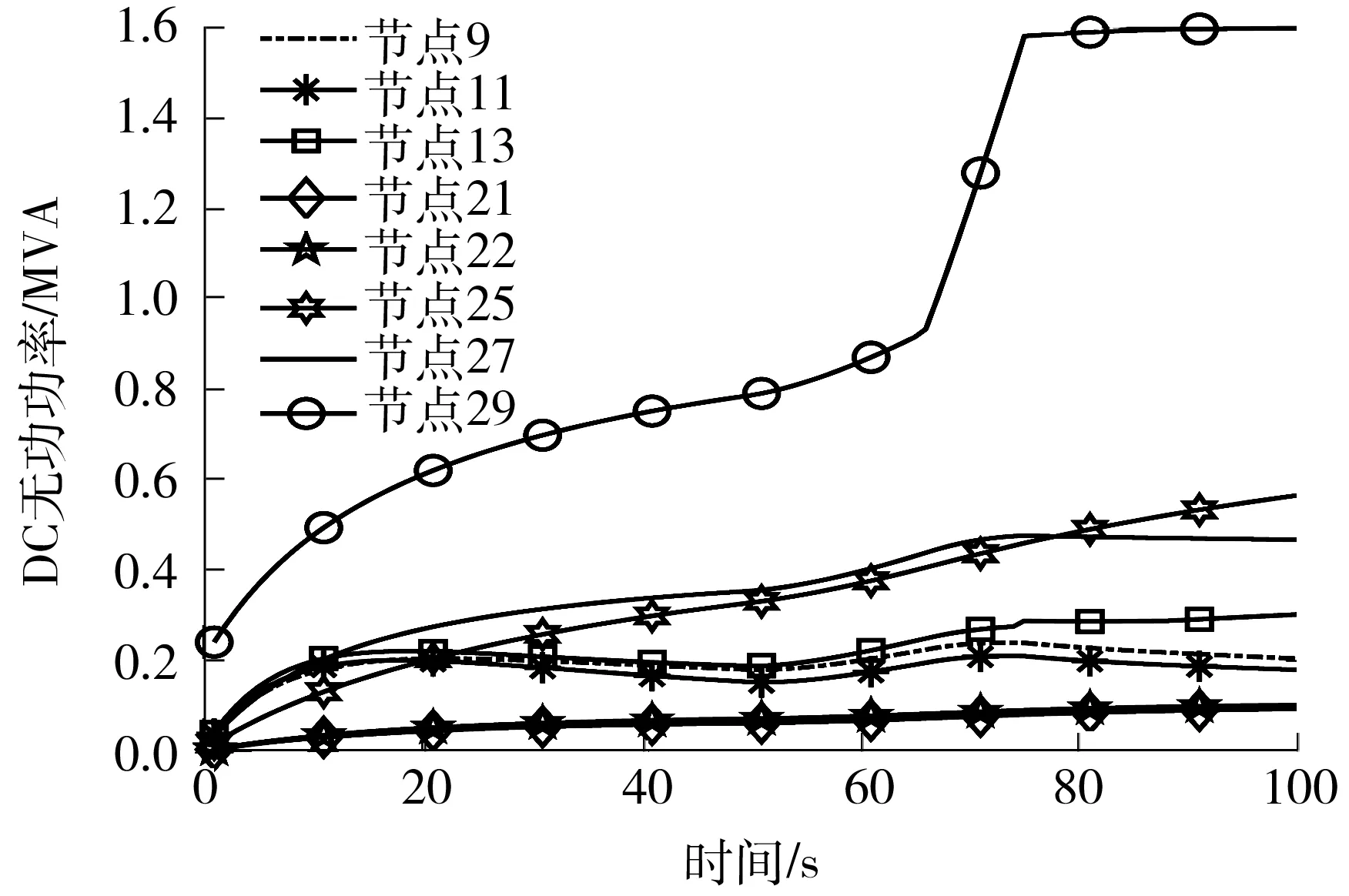
图4 负荷匀速增加时以文中方法进行控制的DG无功功率曲线

在网损方面，从图5可以看出，文中方法在负荷保持稳定的前50 s能将网损逐步降低，直至网损曲线与集中优化得到的最优解重合。在50～75 s之间负载快速增长了50%，导致电压快速下降，直至出现低电压风险。在这个过程中，文中方法的网损曲线一直与最优曲线紧密贴合。这一结果与2.3节的理论分析结果是一致的——算例中电压开始下降时系统网损已经接近最优，并且由于电压是逐步下降的，只要能及时恢复就不会出现距离较远的两个负荷同时出现低电压的情形，此时采用式(30)可以直接算出最优无功输出。因此，虽然文中方法在仿真开始时需要花费比文献[19]中方法更多的时间来将网损降到最低，但二者在负荷爬升阶段没有明显差异。

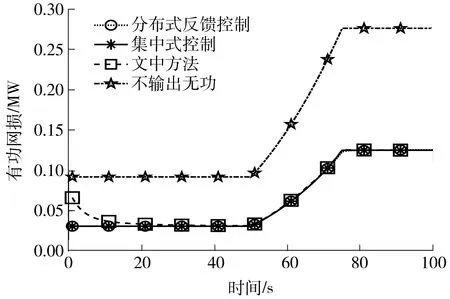
图5 负荷匀速增加时的有功网损曲线

4.2 负荷骤然增加时的无功控制效果

当负荷不是逐步增加，而是在一瞬间提升时，同一时步内可能出现多个电压越限节点，导致由式(30)算出的无功输出偏大。为了验证这种情况下系统是否可以再次到达网损最低的运行点，对4.1节的算例进行修改，前50 s依然保持默认负载不变，51 s时所有负载直接变为原本的1.5倍，直至仿真结束。从图6可以看出，负荷骤增使得系统最低电压在51 s时产生了一个巨大的跳变，采用分布式反馈控制的对照组出现了低电压，经过10 s左右的振荡后从低电压状态恢复。相比之下，采用文中方法没有出现低电压，但网损曲线偏离了集中控制算出的最优解，如图7所示。

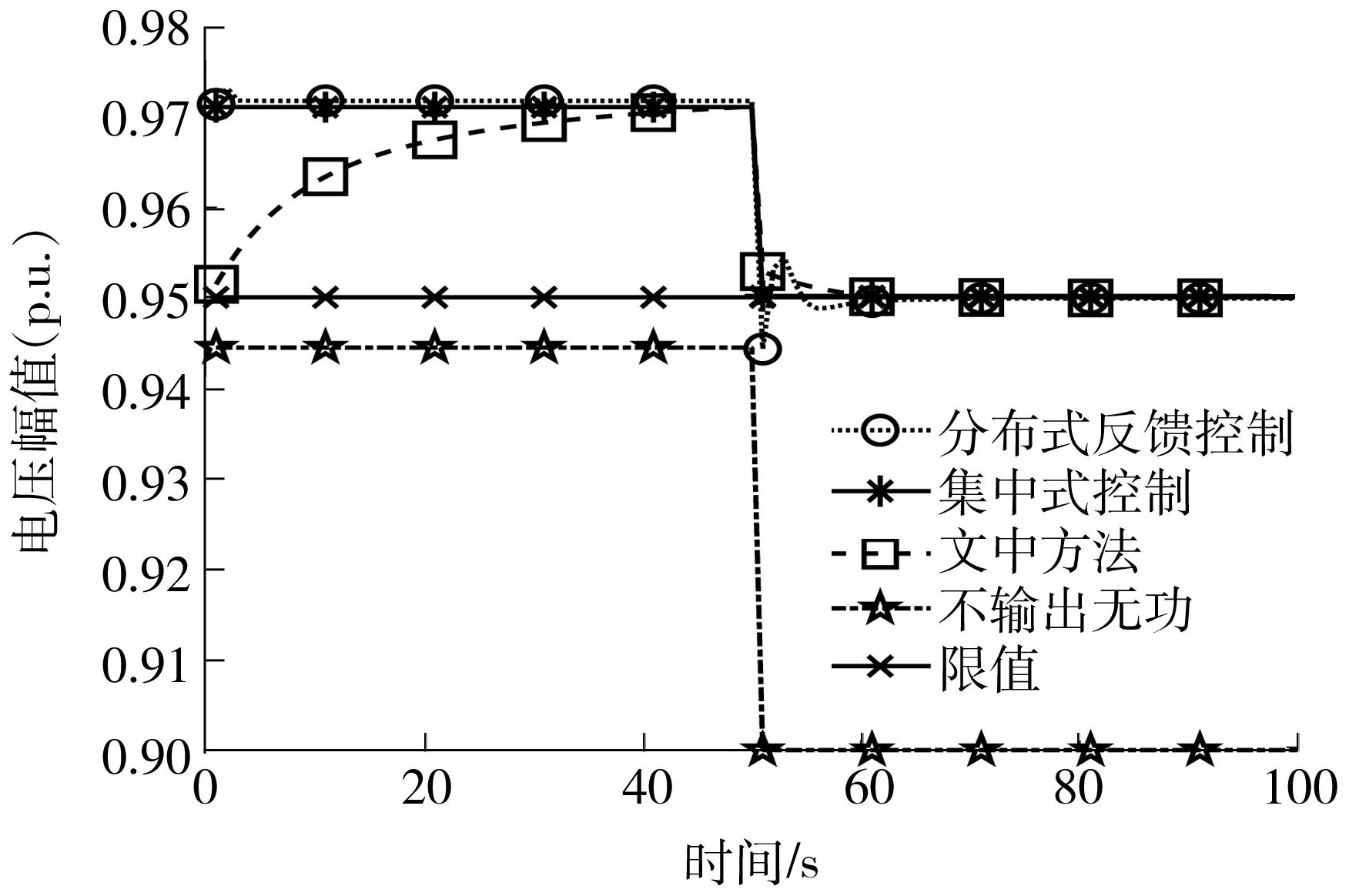
图6 负荷骤然增加时的全网最低电压变化曲线

图7 负荷骤然增加时的有功网损曲线

为了明确电压骤变时的具体情况，图8给出了文中方法的DG无功输出曲线。可以看出，51 s时，节点13和节点29上的DG无功大幅上升，为33节点系统的两个末梢提供电压支撑，避免了电压骤降。由于这两个DG的邻域没有交集，按照2.3节的理论分析，会导致过补偿，表现在仿真结果上就是网损曲线脱离最优解。此后，在式(14)的作用下，这两个DG的无功开始下降，直至网损曲线重新与最优值重合，系统的最低电压也稳定在了0.95 p.u.的邻界值上。可以看出，文中方法在多个负荷节点同时出现低电压问题时依然可以立即使其恢复，因此造成的过度补偿也能在之后快速消除。

图8 负荷骤然增加时以文中方法进行控制的DG无功功率曲线

4.3 负载骤增时运行点离最优较远的情形

前两个例子里，负载上升都出现在50 s之后，此时系统网损在式(14)对应的本地控制下已几乎降到最低。为了验证文中方法在更极端条件下的性能，将负载从仿真开始就设为原始负载的1.5倍，一直持续到仿真结束。这意味着过半的负荷节点都会在一开始出现过电压(如图9所示)，从而导致大部分DG节点在一开始就运行在低电压修复模式。图10示出了从重载状态开始控制时的全网最低电压变化。

图9 重载状态下各节点的初始电压Fig.9 Initial bus voltage under a heavy load level

图10 从重载状态开始控制时的全网最低电压变化曲线

如图11所示，除了21、22、25这3个距离系统末端较远的DG以外，所有DG都在一开始就调高出力，以修复系统末端的低电压，之后逐渐下调直至平稳。整个过程中，负荷电压始终满足限值，网损则逐渐向最优值逼近，如图12所示。可以看出，由于低电压出现的面积太大，文中方法在第一秒时就出现了严重的过补偿，以致于有功网损超过了不输出无功时的情形。然而这一问题在之后的无功控制中很快得到了缓解，网损曲线快速贴近最优值。可见，出现低电压前的初始运行点对文中方法控制过程的影响是有限的，对最终控制效果没有影响。相比之下，基于分布式反馈控制的方法虽然能更快地最小化网损，但需要经过10 s左右的振荡才能逐渐消除低电压问题。

图11 从重载状态开始控制时的DG无功功率曲线Fig.11 DG reactive power curves under a heavy load level

图12 从重载状态开始控制时的有功网损曲线Fig.12 Active power loss curves under a heavy load level

5 结论

文中提出了一种根据负荷低电压警报和DG同步相量策略实现配电网最优无功分散控制的方法。该方法可以在无需用户提供实时负荷曲线等敏感信息的前提下，通过调节DG节点的无功功率，快速修复负荷节点的低电压，并且最大限度地降低系统的有功网损。仿真显示，文中方法在各种场景下都能一步到位地修复系统的低电压问题，而后渐进地将运行点移动到网损最小的位置。其中，当系统负载逐步增加时，文中方法不仅可以持续避免低电压问题，也能让系统继续维持在网损最低的运行点。当系统复杂性突然加大，导致大量负荷节点同时出现低电压问题时，文中方法依然可以立即修复低电压问题，因此造成的过补偿可以在之后快速恢复，从而让系统重新找到最优运行点。