改进的粒子群变异算法在建筑节能优化中的应用

刘刚 王漠 董伟星 黄文龙

(1．天津大学 建筑学院，天津 300072；2.天津大学 天津市建筑物理环境与生态技术重点实验室，天津 300072； 3.天津大学 国际工程师学院，天津 300072；4.中国中建设计集团有限公司，北京 100037)

建筑能耗模型一般是黑箱问题，求解其全局最优值的计算过程复杂，时间成本高。能耗模型一般为多峰值函数，若用优化算法求取其全局最优值，很容易在局部最优时过早收敛。

粒子群算法[1]是一种建筑领域常用的优化算法。针对算法容易陷入局部最优的缺点，建筑领域内的许多研究人员对粒子群算法进行了优化和改进，以解决实际应用中存在的问题。王玲[2]对粒子群算法中惯性权重的动态调整方式进行了改进，优化了变流量空调控制系统的参数，大幅缩短了控制系统的响应时间。吴洲等[3]采用自适应的粒子群算法优化建筑内各窗帘的开启角度，改善了室内光环境和太阳辐射得热，降低了建筑能耗。Rapone等[4]将粒子群算法与能耗仿真软件进行耦合，对办公建筑典型幕墙的参数进行优化，降低了建筑物的碳排放量。曹祥红等[5]将模拟退火的机制结合到粒子群算法中，引入速度收缩因子和轮盘赌策略，优化了公共建筑能耗拆分模型的参数。李建维[6]对惯性权重的取值策略进行改进，对中央空调水系统的运行工况进行优化，实现了系统的整体节能。

近几年粒子群算法的改进工作中，一个主要的方向是引入遗传算法中的变异操作，使用数学分布作为变异算子，在粒子位置的更新过程中进行变异，帮助粒子跳出局部最优区域，以找到全局最优值[7]。在这方面，Higashi等[8]使用高斯分布随机数作为变异算子，Stacey等[9]使用柯西分布随机数作为变异算子，Ling等[10]提出一种基于小波变异的粒子群算法，Thangaraj等[11]则提出一种基于Beta分布的变异方法。

目前，粒子群变异算法主要应用于计算机领域，尚未见到有应用于建筑节能优化问题的报道。多数研究者将研究重点放在了对原理的改进上，只进行了测试函数层面的验证，具体的变异方式和操作并不完全合理。将这样的算法应用到实际问题中时，优化效果往往不够理想。鉴于此，文中拟对粒子群变异算法进行改进，并探究其对建筑节能优化问题的适用性。

1 现有粒子群变异算法概述

1.1 粒子群算法原理

在粒子群算法中，粒子的信息由粒子的位置、速度、适应度来表示，每个粒子都根据自身历史状态以及与全局最优粒子间的关系不断更新自己的速度和位置，每次更新之后使用适应度来评价粒子位置的优劣。

在D维的目标搜索空间中，存在由n个粒子组成的种群X=(X1,X2,…,Xn)，其中第i个粒子的位置为xi，粒子的速度为vi，该粒子当前搜索到的最优位置为pi，整个粒子群的最优位置为pg。更新公式为

(1)

(2)

式中：i=1,2,…,n；维数d=1,2,…,D；ω为惯性权重；c1、c2为学习因子；r1、r2为[0,1]上的随机数；t为粒子群迭代代数。

1.2 粒子群变异算法原理

在粒子位置的更新过程中，可通过某种方式对粒子的位置进行改变，如下式：

(3)

这种完全随机的、不遵循粒子群内部规律和关系的变化，使粒子能够跳出局部最优区域，在求解空间中进行更均匀的探索以找到全局最优点。目前常见的变异方式有4种。

(1)高斯变异

Higashi等[8]提出的高斯变异算法使用下式进行变异：

(4)

式中：gaussian(σ)为取自高斯分布的随机数；σ为高斯分布的标准差，取值为搜索空间范围的0.1倍。

(2)柯西变异

Stacey等[9]提出的柯西变异算法使用下式进行变异：

(5)

文中通过经验观察将γ的值取为0.2。

(3)小波变异

Ling等[10]提出的小波变异粒子群算法的变异方式如下：

(6)

式中，w(φ)为小波函数值，pmax、pmin为粒子搜索空间的上界和下界。小波变换的函数有许多种，文中选择Morlet小波作为小波基，其具体形式如下：

w(φ)=e-φ2/2cos (5φ)

(7)

φ为[-2.5,2.5]间的随机数。

(4)Beta变异

Thangaraj等[11]提出的Beta分布变异方法的具体形式如下：

(8)

式中，b为服从Beta分布的随机数，α和β均为Beta分布的参数。

图1为粒子群变异算法的流程图，与标准粒子群算法的流程相比，区别主要是增加了步骤3和4，来对是否发生变异进行判断并实现变异操作。

图1 粒子群变异算法的流程Fig.1 Flow chart of particle swarm mutation algorithm

2 对现有粒子群变异算法的改进

2.1 基于变异操作的改进

文中针对现有变异方式和操作的不合理之处，基于将变异算子与粒子群算法结合的思想，对算法中具体的变异操作进行改进，提出一种新的变异操作：

(9)

ε为取自上述4类数学分布的随机数，r取[-1,1]区间内的随机数。

如图2所示，对上述4种分布的参数进行调整以及放缩、平移变换，可以得到改进后的分布。

2.2 测试函数实验与分析

文中选取了表1所示的3个最常用的评价单目标寻优算法有效性的测试函数[7]进行实验。这3个函数均为多峰值函数，具有多个局部最优点，对于建筑能耗模型有一定的代表性。它们均在自变量[0,0,0,…,0]点处取得全局最优值0。

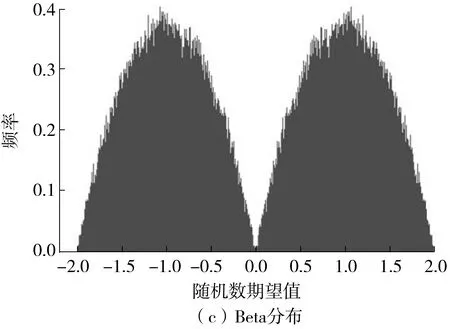
图2 改进后的4种数学分布Fig.2 Four types of improved mathematical distribution

表1 测试函数Table 1 Test functions

算法的参数设置如表2所示，均选择粒子群算法最常用的参数，其中加速度常数取自文献[1]，迭代次数、粒子数量、惯性权重变化范围、速度限值分别为文献[8]、[9]、[10]、[11]中使用次数最多的取值，变异率(取0.5)是一个较为均衡的取值[7]，搜索空间维度取决于自变量的个数。

表2 算法参数设置Table 2 Parameters setting of algorithms

为便于在后续实验中对比变异算法的效果，文中对变异策略进行了统一：

①粒子适应度的全局最优值持续5代不变，引入一次变异；

②对粒子的位置进行变异，粒子位置的每个维度都按照变异率发生变异；

③比较粒子变异前后的适应度值，若变异使粒子的适应度变差，则恢复变异前的位置。

文中所有实验使用Python编程语言完成，编程平台采用PyCharm，编程环境为Python 3.7。伪代码如下所示(文中程序均在Windows10系统中运行，Intel(R)Core(TM) i7- 7700HQ@2.80 GHz，16.0 GB内存)：

while iteration<=max_iteration do

begin

j=0

for each particleido

begin

calculate its fitness value

if fitness value is better than its best fitness value in history

then updatepi

if the fitness value is better than best fitness value of population in history

then updatepg

calculateviaccording equation(1)

updatexiaccording to equation(2)

end

if fitness value change

thenj=0

else fitness value not change

thenj=j+1

ifj==5

then for each particleido

begin

for each dimensionddo

begin

p=random number from[0,1]

ifp>mutation possibility

end

j=0

if fitness value not better than before

thenxinot change

calculate fitness value

if fitness value is better than its best fitness value in history

then updatepi

if the fitness value is better than the best fitness va-lue in history

then updatepg

end

outputpgand best fitness value of population

使用标准粒子群算法、4种现有粒子群变异算法以及对应的4种改进后的算法进行测试函数实验。选取目标函数的平均值和能够找到目标函数全局最优值的次数(即收敛次数)作为评价标准。目标函数值小于0.01即认为找到全局最优值。

表3为9种算法在3个测试函数上分别运行50次的实验结果。相对于标准粒子群算法而言，改进前的4种算法中，对于Ackley函数，只有柯西变异的平均值稍低，其余算法的结果均比较差；对于Griewank函数，高斯变异、柯西变异、小波变异的优化效果稍好，Beta变异则较差；对于Rastrigin函数，高斯变异和柯西变异的平均值稍低一些，其余均较差。

表3 测试函数实验结果Table 3 Results of test function experiment

从表3中可以看出，相对于标准粒子群算法,现有的粒子群变异算法的寻优结果并没有本质性的改善，有些情况下甚至会导致优化效果变差。使用标准粒子群算法以及现有粒子群变异算法的有效性较差，用于优化建筑节能问题是不能满足要求的。

但是变异方式得到改进之后，3种函数的目标函数平均值显著降低，收敛次数大幅增加。这初步表明变异方式的改进是有效的。4种变异算法的性能大体相近，不存在本质性的差别。对于Ackley函数，柯西变异的效果稍差于其他3种变异方式。对于Griewank函数，柯西变异与Beta变异的效果稍好于高斯变异与小波变异。对于Rastrigin函数，小波变异和柯西变异的效果好于高斯变异和Beta变异。

3 优化案例

3.1 问题的引出

商业综合体建筑目前在我国发展迅速，数量庞大。这类建筑的体量特点是单层面积较大，层数较少，呈扁平状。由于人流量大、商业活动频繁，这类建筑的能耗非常大。商业建筑的节能优化应用范围很广，具有代表性。

太阳辐射得热是影响建筑能耗的重要因素，合理地控制形体参数和材料种类来调整太阳辐射得热量是建筑节能的重要手段，因此，笔者认为商业综合体建筑的太阳辐射得热优化可以代表一般的建筑节能优化问题。

3.2 商业建筑标准模型的建立

根据寒冷地区近10年新建的40座商场的调研数据[12]，选定参数如表4所示。在Grasshopper参数化平台建立建筑模型，如图3所示。

表4 商场标准模型参数Table 4 Parameters of standard model of a commercial building

图3 商业综合体建筑模型Fig.3 Model of a commercial building

3.3 太阳辐射得热模型的建立

首先假设一种理想的设计环境：建筑周围无遮挡，围护结构各层材料均为均质材料。共选取9个影响太阳辐射得热量的建筑参数，相关情况总结于表5。

表5 自变量参数表Table 5 Parameters of independent variables

外墙、侧窗、屋顶和天窗的材料类型及太阳能吸收系数均取自文献[13]。窗墙比与屋顶透光面积比的取值范围取自GB 50189—2015《公共建筑节能设计标准》[14]。

建筑的太阳辐射得热量HG由下式计算：

HG=∑kiSiRi

(10)

式中，Si为建筑各面接受太阳辐射的面积，Ri为单位面积太阳辐射得热量，ki为各围护结构材料的太阳能辐射吸收系数。

使用Grasshopper参数化平台上的EnergyPlus插件模拟夏季和冬季的单位面积太阳辐射量(夏季取6—8月，冬季取当年11月—次年1月)，所得结果见表6。

在天津地区，理想状态为夏季得热量HGsummer取最小值，冬季得热量HGwinter取最大值[15]。此外，因文中研究的是单目标函数的优化问题，故取目标函数为夏季得热量与冬季得热量之差，求其最小

表6 单位面积太阳辐射量Table 6 Solar radiation per unit area

值，即目标函数为

HG=HGsummer-HGwinter

(11)

目标函数表示太阳辐射得热对建筑能耗的影响程度。将上述常量数值与自变量对应变量标记代入，得到

HG=(x2-x1)(190 675x5+245 525x6-

402 100x7+228 050x8)+262 150x1+

4 642 600[x3+x9(x4-x3)]

(12)

该目标函数是一个多峰值的数学模型，存在一个全局最优点和多个局部最优点，当自变量x=[0.92,0.16,0.52,0.37,0.70,0.70,0.20,0.70,0.20]时，目标函数取得最小值2 223 790.2 kW·h。

3.4 实验与分析

对标准粒子群算法和4种改进后的粒子群变异算法分别进行50次重复实验，评价指标包括寻优结果的平均值、标准差、收敛率以及收敛速度，实验结果见表7与图4。

1)斜线前数字表示大部分实验的最大收敛代数，斜线后数字表示全部实验的最大收敛代数。

本节实验条件和参数设置均与3.3节完全相同，Python代码仅在自变量及目标函数部分进行了相应的修改。

从实验结果可以看出，对于商业建筑的太阳辐射得热优化问题，4种改进后的粒子群变异算法相对于标准粒子群算法，目标函数平均值降低了1.3%以上，收敛率至少提高了3倍，寻优效果明显优于标准粒子群算法。从平均值和收敛率来看，柯西变异和Beta变异要优于高斯变异和小波变异;从收敛速度来看，小波变异要优于其他3种变异方式;从标准差来看，高斯、柯西、Beta变异要优于小波变异。

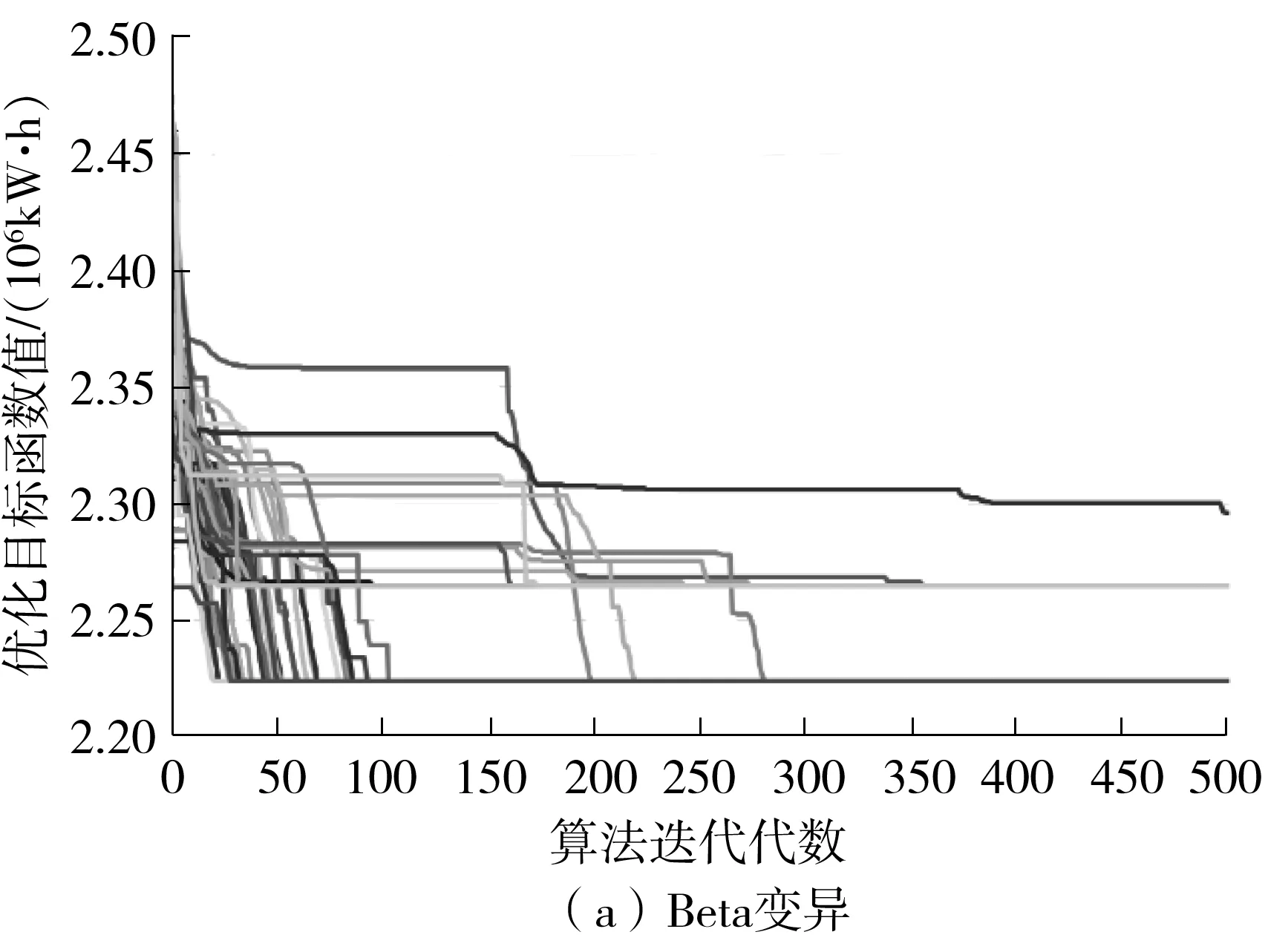
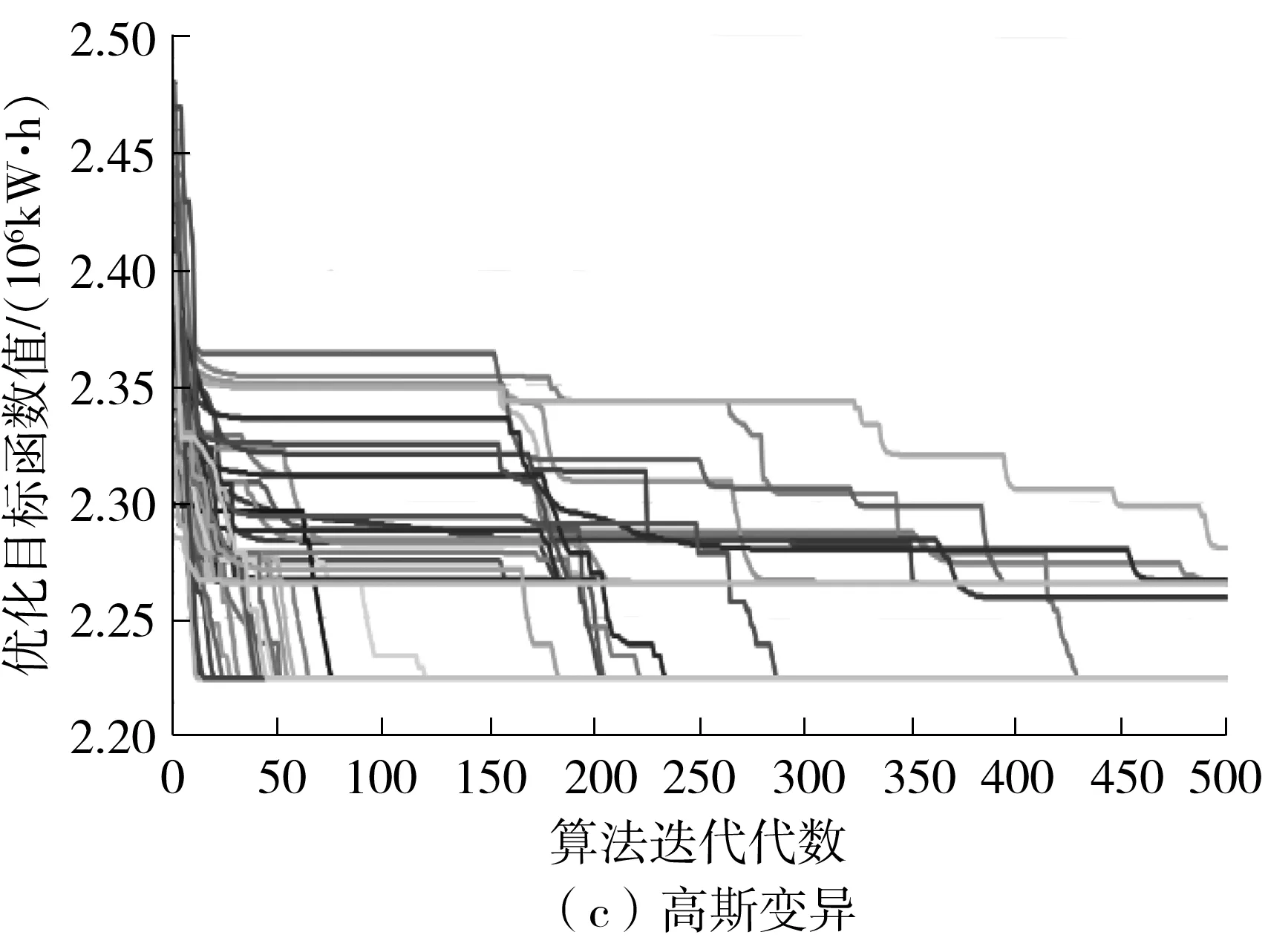
图4 目标函数值随收敛代数的变化趋势

改进算法有效的原因主要有三点：其一是变异随机数的分布范围更加均匀合理，可以为粒子位置提供多种变异步长，粒子不论遇到大或小的局部最优区域，都有更大的概率从其中跳出，并且避免粒子位置经常超出求解空间，从而降低变异操作的有效性；其二是变异既能向正向进行，也能向反向进行，并且概率相同，粒子经过变异可以更全面地探索求解空间；其三是粒子位置绝对值的增大变异与减小变异的概率是相同的，为粒子均匀遍布求解空间提供了更多的可能性。

4 结语

为克服现有粒子群变异算法的缺陷，文中对4种粒子群变异算法的变异操作进行了改进，并使用测试函数和建筑节能优化案例验证了改进的有效性。现有粒子群变异算法的有效性较差，相对于标准粒子群算法寻优能力没有显著提高，主要原因是变异方式以及参数设置不合理。对于测试函数实验以及文中的建筑节能优化问题，使用改进的粒子群变异算法可以使目标函数值更低、收敛率更高，该算法可以在一般建筑节能优化问题中推广。

4种粒子群变异算法的优化效果互有长短。目标函数值、寻优速度、稳定性三者之间的矛盾，还需要建筑师根据实际要求做进一步的权衡取舍。

本文的局限性体现在3个方面：

①仅考虑了形体和材料对建筑太阳辐射得热量的影响，涉及的参数较少，仅根据简化的模型从原理方面说明改进的粒子群变异算法对于建筑节能问题的优化效果具有本质性的改善，未涉及复杂的计算和模拟过程；

②仅使用了最常见的算法参数和变异策略，没有探讨算法参数和变异策略对于优化效果的影响；

③仅讨论了商场建筑节能优化问题，未针对其他类型的建筑进行实验，不同类型的建筑能耗模型具有不同的特点，文中改进算法的适用性和优化效果可能会稍有差异。

未来的研究工作将围绕更细致的建筑参数以及不同的算法参数、变异策略、建筑类型来展开，进一步探讨改进粒子群变异算法在建筑节能优化领域内的适用性问题。