改进的格网惯导系统无阻尼综合校正方法

黄卫权，方涛，王宗义

哈尔滨工程大学 自动化学院，哈尔滨 150001

为克服指北方位惯性导航系统(Inertial Navigation System, INS)在高纬度地区定位与定向的困难，以格网坐标系为导航坐标系的格网INS力学编排被提出并经过理论验证可作为船舶在高纬度地区导航的可靠方案[1-2]。惯性器件测量误差、初始对准误差等误差源的存在导致INS导航误差随时间积累严重，其中陀螺漂移是导致误差积累的主要因素。随着导航时间的延长，单纯依靠INS自主工作难以长时间持续为载体提供可靠的姿态、速度和位置信息[3-6]。

组合导航技术可有效抑制INS随时间积累的误差[7-8]，但对于在海上航行的船舶而言，长时间获取外部导航信息是不允许的，并且将极大地降低船舶的导航自主性。从保持船舶导航自主性的角度出发，综合校正技术作为一种有效的误差抑制手段被广泛应用于长航时船用INS中，该技术旨在通过有限的外部导航信息对陀螺漂移进行估计和补偿来抑制INS的误差[9-11]。当有限的外部导航信息为间断信息时，称为点校，如两点校、三点校和点点校。

目前，大多数点校算法均需要在阻尼条件下进行。文献[12]最早提出了在阻尼条件下进行的适用于平台式INS的两点校、三点校以及点点校方案。在此基础上，针对捷联式INS，文献[13]提出了在位置信息辅助下的三点校方案，对方位陀螺漂移进行了估计和补偿。文献[14]根据全阻尼INS误差传播规律，在间断的位置信息辅助下估计并补偿了导致误差发散的等效陀螺漂移。针对高纬度地区的捷联式INS，文献[15]延续文献[13]的思路提出了横坐标系INS的三点校方案。文献[16]在阻尼条件下设计了格网INS的两点校和三点校方案。通常阻尼需要借助外部速度进行[17-18]，而外部测速设备如多普勒计程仪(Doppler Velocity Log, DVL)是通过向外发射信号的形式测量速度[19-20]。阻尼条件下进行的综合校正方案需要在校正期间长时间获取外部速度辅助，是以牺牲惯导系统导航自主性和隐蔽性为代价的，该类方案在船舶需保持静默航行状态下无法实施，不具备普适性。为确保综合校正在无阻尼条件下进行，文献[20]将外部位置和速度与INS组合通过卡尔曼滤波技术估计水平姿态误差角，进而反馈修正水平姿态误差以保证综合校正在无阻尼条件下进行，该方法本质上仍然属于阻尼条件下的综合校正。阻尼条件下的综合校正是从抑制水平姿态误差的角度进行综合校正，而阻尼无法抑制加速度计零偏所造成的水平姿态误差这一事实也就成为影响陀螺漂移估计精度的重要因素。文献[21]将外部速度与格网INS组合,通过卡尔曼滤波技术估计水平姿态误差角，将估计结果作为位置和航向误差的修正量引入到综合校正过程以保证综合校正在无阻尼条件下进行。该方案有效地缩短了外部速度信息的使用时间，同时由于保证了舒勒调整条件，船舶航行不受运动状态的限制。该方案中组合滤波方式仍然无法估计出加速度计零偏所造成的水平姿态误差，因而陀螺漂移的估计精度仍受限于加速度计零偏。

文献[22]提出了在全球定位系统(Global Positioning System, GPS)提供的速度信息辅助下的姿态和加速度计零偏的参数估计方法。文献[23] 提出了在DVL提供的速度信息辅助下的姿态估计方法，基于此，本文提出一种改进的格网INS无阻尼两点校方案。首先在文献[23]基础上，参考文献[22]中的思路，将加速度计零偏纳入被估计参数，在格网坐标系框架下推导了DVL辅助下的姿态和加速度计零偏的参数估计目标函数，进而采用牛顿迭代最优化方法对姿态和加速度计零偏进行估计。综合校正前，在DVL辅助下估计和补偿加速度计零偏以抑制由其所造成的水平姿态误差对综合校正中陀螺漂移估计精度的影响。其次在两次间断的外部位置和航向的辅助下设计了无阻尼综合校正方案对陀螺漂移进行估计，接受校正信息时刻处所涉及到的水平姿态误差由本文所推导的参数估计方法估计得到。仿真及实验结果表明：所设计的方案进一步缩短了DVL使用时间，同时加速度计零偏的补偿显著地提高了陀螺漂移的估计精度，补偿惯性器件测量误差有效地抑制了格网INS随时间积累的导航误差。

1 姿态和加速度计零偏的参数估计方法

在格网坐标系框架下，本节首先推导了DVL辅助下的加速度计零偏和姿态的参数估计目标函数，进而介绍了牛顿迭代最优化参数估计方法。本文将3次使用该参数估计方法：第1次在综合校正前估计并补偿加速度计零偏以抑制水平姿态误差；第2次和第3次分别在接受外部校正信息的200 s时间内估计水平姿态，将估计的等效水平姿态误差引入无阻尼两点校过程。本文所涉及的坐标系及其定义如下：

1) 载体坐标系b。载体坐标系原点Ob位于船舶质心,zb轴垂直于船舶的甲板平面，xb轴指向船舶的右舷，yb轴指向船艏，构成右手坐标系。载体坐标系如图1所示。

2) 惯性坐标系i。惯性坐标系原点位于地球质心,xi轴位于赤道平面内并指向某一恒星，yi轴位于赤道平面内并垂直于xi轴，zi轴与地轴重合，构成右手坐标系。

3) 地心地固坐标系e。地心地固坐标系原点位于地球质心,ze轴沿地轴方向，xe轴在赤道平面与格林威治子午面的交线上，ye轴也在赤道平面内与xe、ze轴构成右手坐标系。惯性坐标系和地心地固坐标系如图2所示。

4) 格网坐标系G。格网坐标系原点OG位于船舶质心,yG轴位于当地水平面指向北并平行于格林威治子午面，xG轴位于当地水平面指向东并垂直于yG轴，zG轴垂直于当地水平面与yG、zG轴构成右手坐标系。格网坐标系如图3所示，图中格网平面平行于格林威治子午面。

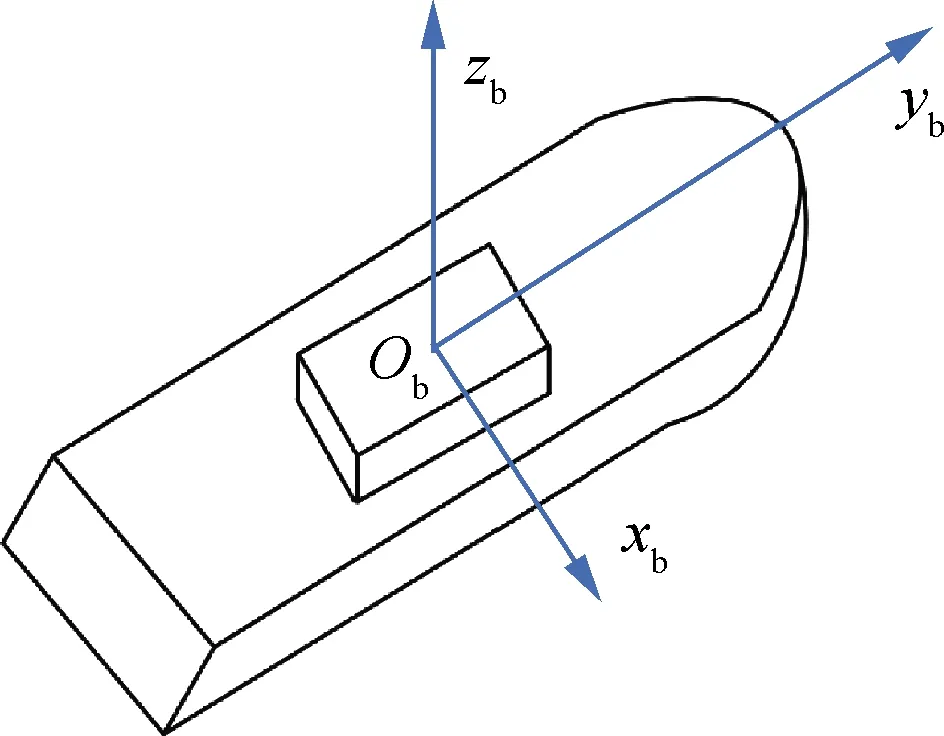
图1 载体坐标系Fig.1 Body frame

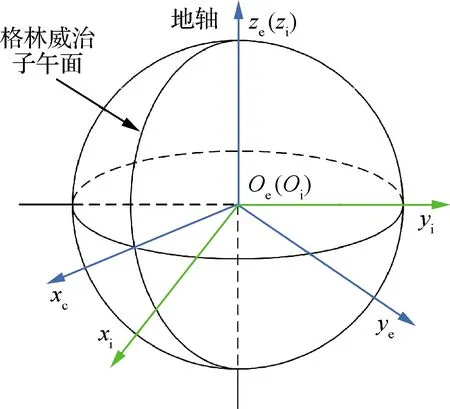
图2 地心地固坐标系和惯性坐标系Fig.2 Earth centered-earth fixed frame and inertial frame

图3 格网坐标系Fig.3 Grid frame

1.1 参数估计目标函数

格网坐标系下的姿态和速度微分方程为

(1)

(2)

由式(1)，速度微分方程可进一步表示为

(3)

(4)

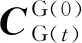
(5)

(6)

将式(4)代入式(3)可得：

(7)

在[0,t]时间段内对式(7)两侧进行积分：

(8)

结合式(6)，左侧第1个积分项可计算为

(9)

式中：Vb(0)表示载体坐标系下的初始速度。

将式(9)代入式(8)可得：

(10)

(11)

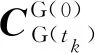
(12)

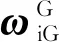
(13)

(14)

式中：δθ1、 δθ2为[tk,tk+1]时间段内第1和第2次陀螺输出的等效角增量信息；δv1、 δv2为[tk,tk+1]时间段内第1和第2次加速度计输出的等效速度增量信息。式(14)的详细计算过程可参考文献[22]。

为表示方便，令

(15)

(16)

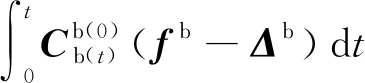
(17)

结合式(12)和式(17)，式(10)可表示为

(18)

为表示方便，令

(19)

(20)

则参数估计目标函数为

(21)

(22)

为了表述方便，仍然使用式(21)的形式表示重构后的参数估计目标函数：

(23)

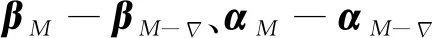
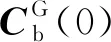
(24)

与四元数乘法相关的矩阵为

(25)

式(23)的等价形式为

(26)

式中：α、β和κΔb在此处转换为标量为0的四元数。

进一步地，文中的参数估计问题可转化为有约束条件的最小化参数估计问题：

(27)

1.2 牛顿迭代法

牛顿迭代法可作为解决有约束条件的最小化参数估计问题的有效手段。引入拉格朗日乘子ξ，则式(27)可通过拉格朗日算子表示为

(28)

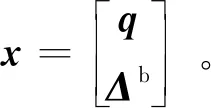
(29)

式中：迭代增量δx和δξ的计算方式为

(30)

详细的计算可参考文献[22]中给出的姿态和参数估计递归算法，本文不再赘述。

2 P方程和ψ方程

P方程和ψ方程是设计综合校正策略的核心方程。P方程建立起位置误差、格网航向误差与平台漂移角之间的关系；ψ方程建立起平台漂移角与陀螺漂移之间的关系。针对格网INS，文献[21] 给出了适用于无阻尼条件下进行综合校正的P方程：

(31)

ψ方程为

(32)

3 综合校正方案

在两次间断的外部位置和航向信息辅助下，本文设计了相应的两点校策略,外部位置由GPS提供，外部航向由天文导航系统(Celestial Navigation System, CNS)提供。在综合校正前的某一时间段内，在DVL的辅助下，通过第1节中设计的参数估计方法对加速度计零偏进行估计和补偿。通常现代船舶一般都装备有DVL，由于该参数估计方法所需时间较短，因而船舶在开始导航后即可进行加速度计零偏的估计和补偿。需要指出的是，本文所设计的参数估计方法在估计航向的精度方面性能有限，因而并不将估计出的航向引入综合校正过程。DVL、GPS和CNS引入INS的时间如图4所示。图中虚线中的实线和实心原点表示向INS引入外部导航信息的时间，需要强调的是本文所设计的参数估计方法在200 s时间内即可准确地估计出加速度计零偏和姿态。

图4 3种导航系统信息引入INS的时间Fig.4 Time for introducing three types of navigation information to INS

设INS在t1和t2时刻接收外部校正信息。由式(32)可得t1～t2时间段内的ψ角增量为

(33)

由式(31)可得t1～t2时间段内ψ角增量的另一种计算形式

δψ=M-1(t2)P(t2)-M-1(t1)P(t1)

(34)

在t1时刻，根据外部提供的位置和航向对INS进行位置和航向重调，同时根据前述参数估计方法估计出的水平姿态对水平姿态进行重调。则式(34)可简化为

δψ=M-1(t2)P(t2)

(35)

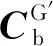
(36)

由式(36)可计算得到等效的姿态误差φx、φy和φz，进而可计算得到P(t2)。

由式(33)和式(35)可计算得到εb：

(37)

由式(37)估计出陀螺漂移后对陀螺漂移进行补偿，同时对位置、姿态和速度进行重调即可完成综合校正过程。

4 仿真及实验结果及分析

本文分别采用数值仿真和实验的形式对所设计的两点校方案进行验证。

4.1 数值仿真结果及分析

仿真条件设置如下：仿真时长25 h；陀螺常值漂移为0.01 (°)/h，随机漂移为白噪声；加速度计常值零偏为100 μg，随机零偏为白噪声；船舶初始位置为(85°N, 18°E)；船舶以10 m/s的速度向正北方向运动；姿态设置为正弦函数变化；对准后失准角为6″、6″和6′；外部位置误差标准差为10 m；外部航向误差标准差为10″；辅助速度信息误差为白噪声。

t=3 h时，在DVL的辅助下完成加速度计零偏的估计和补偿以及水平姿态的估计和重调。为确保参数估计的收敛，参数估计在t=3 h前持续200 s。加速度计零偏的估计结果如图5所示。

由图5可知，在200 s时间内，所设计的参数估计方法可准确地估计出加速度计零偏，在t=3 h 时补偿加速度计零偏可有效地抑制由其所造成的水平姿态误差。

t=6 h和t=8 h时，INS两次接收外部位置和航向，同时在t=6 h和t=8 h的前200 s时间内，在DVL的辅助下估计水平姿态并引入综合校正过程。由于在t=3 h后加速度计零偏造成的水平姿态误差得到了有效抑制，相对于未进行加速度计零偏补偿的情况，在接收校正信息前的短时间内本文所提出的方案中水平姿态的估计精度应该更高。以t=6 h前200 s为例，t=6 h前200 s水平姿态估计误差如图6所示：

如图6所示，由于加速度计零偏得到了有效的补偿，所提出的方案在接受校正信息前的200 s内具备更高的水平姿态估计精度。为验证所设计的综合校正方案在陀螺漂移估计和抑制导航误差方面的优势，对包含本文所设计方案在内的4种解算方案进行仿真分析，4种方案如表1所示。

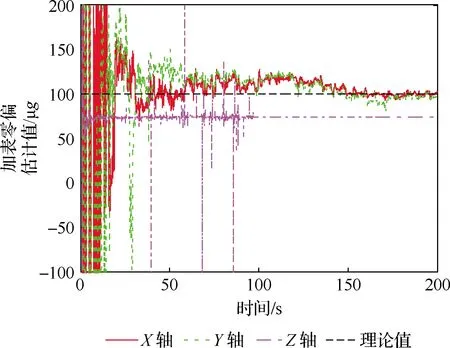
图5 加速度计零偏估计值Fig.5 Estimation results of accelerometer biases

图6 200 s内水平姿态估计误差Fig.6 Estimation errors of level attitudes in 200 s

表1中方案1即为常规的无阻尼INS解算。方案3与文献[21]中设计的无阻尼两点校方案相同，区别在于本文所设计的方案采用第1节中提到的参数估计方法对水平姿态进行估计，而文献[21] 则采用卡尔曼滤波技术估计水平姿态误差。方案4即为本文所设计的综合校正方案。方案3、方案4和文献[21]中方案的陀螺漂移估计值如表2所示。

由表2可知，方案3取得了与文献[21]中方案相当的陀螺漂移估计精度。文献[21]中滤波器单次需要20 min以确保水平姿态误差估计稳定收敛，两点校总共需要40 min的DVL辅助，而本文所设计的参数估计方法单次仅需要200 s的DVL辅助即可保证水平姿态估计稳定收敛，3次参数估计总共需要10 min的DVL辅助，因而采用该方法进一步地缩短了DVL的辅助时间。方案4取得了更高的陀螺漂移估计精度，原因分析如下：方案3中的参数估计方法并不能估计出加速度计零偏所造成的等效水平姿态误差。由于方案4在综合校正前补偿了加速度计零偏，在综合校正阶段相对于方案3具备更高的水平姿态估计精度，因此方案4取得了更高的陀螺漂移估计精度。

表1 4种解算方案Table 1 Four types of solution schemes

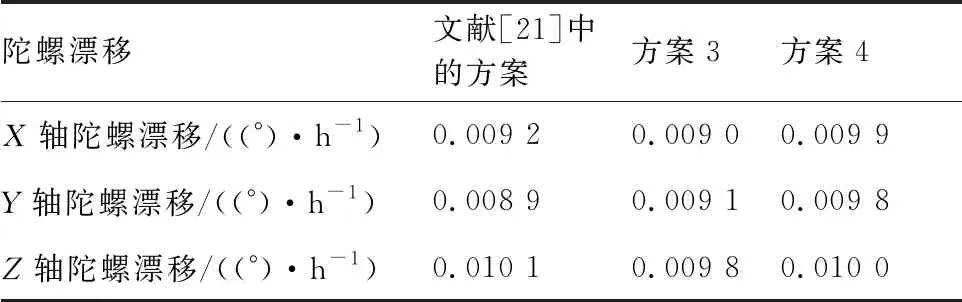
表2 3轴陀螺漂移估计值Table 2 Estimation results of three-axis gyroscope drifts

表1中4种方案的格网姿态误差、格网水平速度误差以及位置误差如图7所示。

t=8 h后4种方案导航误差的均方根统计值如表3所示。

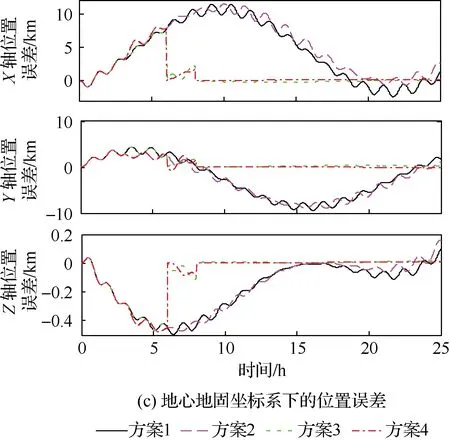
图7 姿态、速度和位置误差Fig.7 Attitude, velocity and position errors

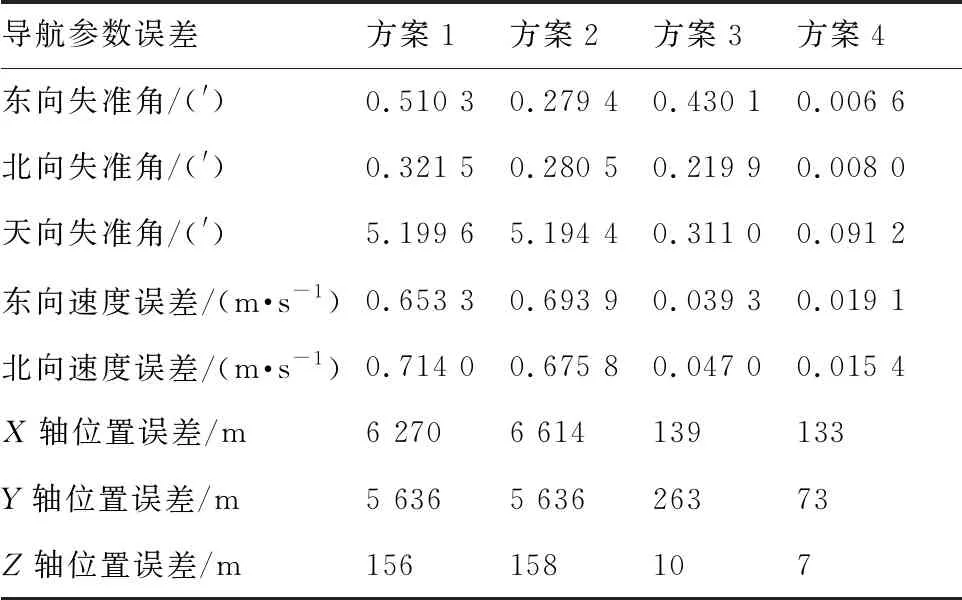
表3 t=8 h后4种方案导航误差的均方根统计值

由图7和表3可知，方案2由于在t=3 h后补偿了加速度计零偏，相较于方案1，稳态水平姿态误差得到了有效抑制(振荡更靠近X轴)，同时由仿真结果可以看到，仅补偿加速度计零偏无法抑制航向、速度及位置误差。方案4由于补偿了陀螺漂移，格网INS随时间积累的误差在校正点后得到了有效的抑制。相对于方案3，方案4的陀螺漂移估计精度更高。这样由于陀螺漂移补偿更彻底，加速度计零偏同时也得到了有效的补偿，方案4更好地抑制了积累的导航误差。综上所述，所设计的综合校正方案进一步地缩短了综合校正过程中DVL的辅助时间，有效地解决了加速度计零偏所造成的水平姿态误差影响陀螺漂移估计精度这一问题，更好地抑制了格网INS随时间积累的导航误差。

4.2 实验结果及分析

本文采用3轴转台摇摆实验对所设计的综合校正方案进行验证。实验场景如图8所示。

激光惯导系统安装于3轴转台上，安装误差已补偿，转台3轴进行等幅正弦摇摆，转台位置为(45.779 6°N, 126.670 5°E)。激光惯导系统在室温条件下热开机后完成初始对准，导航时长11 h，在t=4 h和t=6 h接入位置和航向辅助信息，位置辅助信息由转台位置叠加误差仿真得到，误差标准差设置为10 m；航向辅助信息由转台同步输出航向叠加误差仿真得到，误差标准差设置为10″。惯导系统在t=1,4,6 h的前200 s时间内接入DVL信息估计加速度计零偏和水平姿态，DVL测速由零速叠加真实海试实验测速误差得到。所给出的海试实验测速统计结果给出了DVL和GPS的对地速度，以GPS测速为参考，某一段200 s时间内DVL在载体纵轴方向上的测速误差如图9所示。

本文方案在综合校正前完成了加速度计零偏的补偿，4.1节中的仿真测试是建立在加速度计零偏不变的前提条件下。事实上，惯性器件测量误差会随着时间发生变化，因而后续加速度计零偏的变化会直接影响水平姿态误差的抑制效果，进而影响陀螺漂移的估计精度。幸运的是，针对船舶导航所用的高精度加速度计而言，即使在综合校正期间加速度计零偏发成了变化，由于仍有部分加速度计零偏被补偿掉，其对综合校正仍将产生积极效果。t=1 h和t=6 h处3轴加速度计零偏的估计值如图10所示。

图8 实验场景Fig.8 Experiment scenario

由图10可知，X轴和Z轴加速度计零偏在2个时刻处的估计值基本一致，因而在t=1 h处补偿X轴和Z轴加速度计零偏对综合校正方案是有益的。Y轴加速度计零偏的估计值由13 μg变化为39 μg，显然在t=1 h处补偿后的加速度计输出仍将对综合校正方案产生积极效果。以转台的位置和同步输出的姿态信息为参考，表1中4种方案的姿态误差、速度误差和位置误差如图11所示。

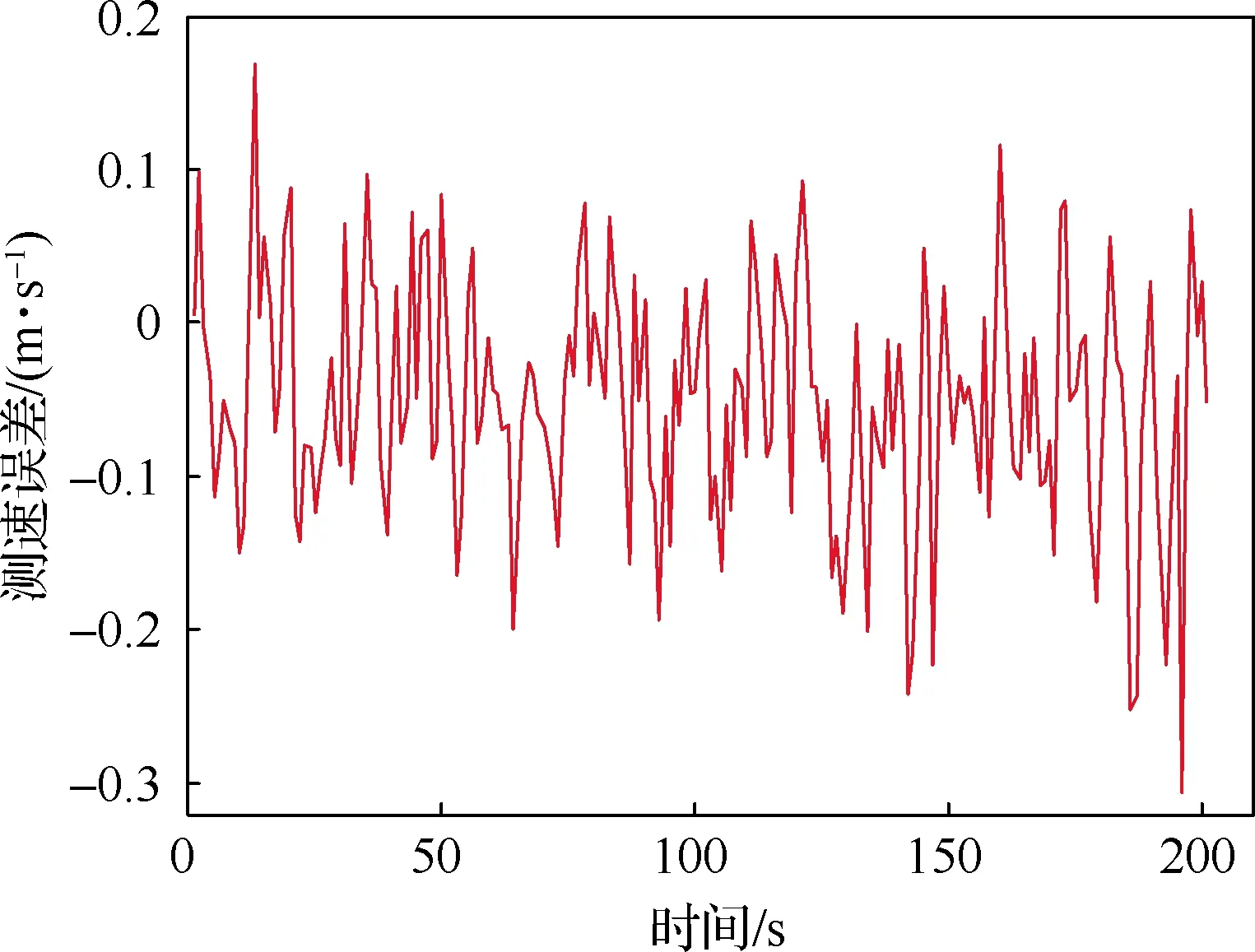
图9 海试实验中DVL测速误差Fig.9 DVL measurement error in sea test

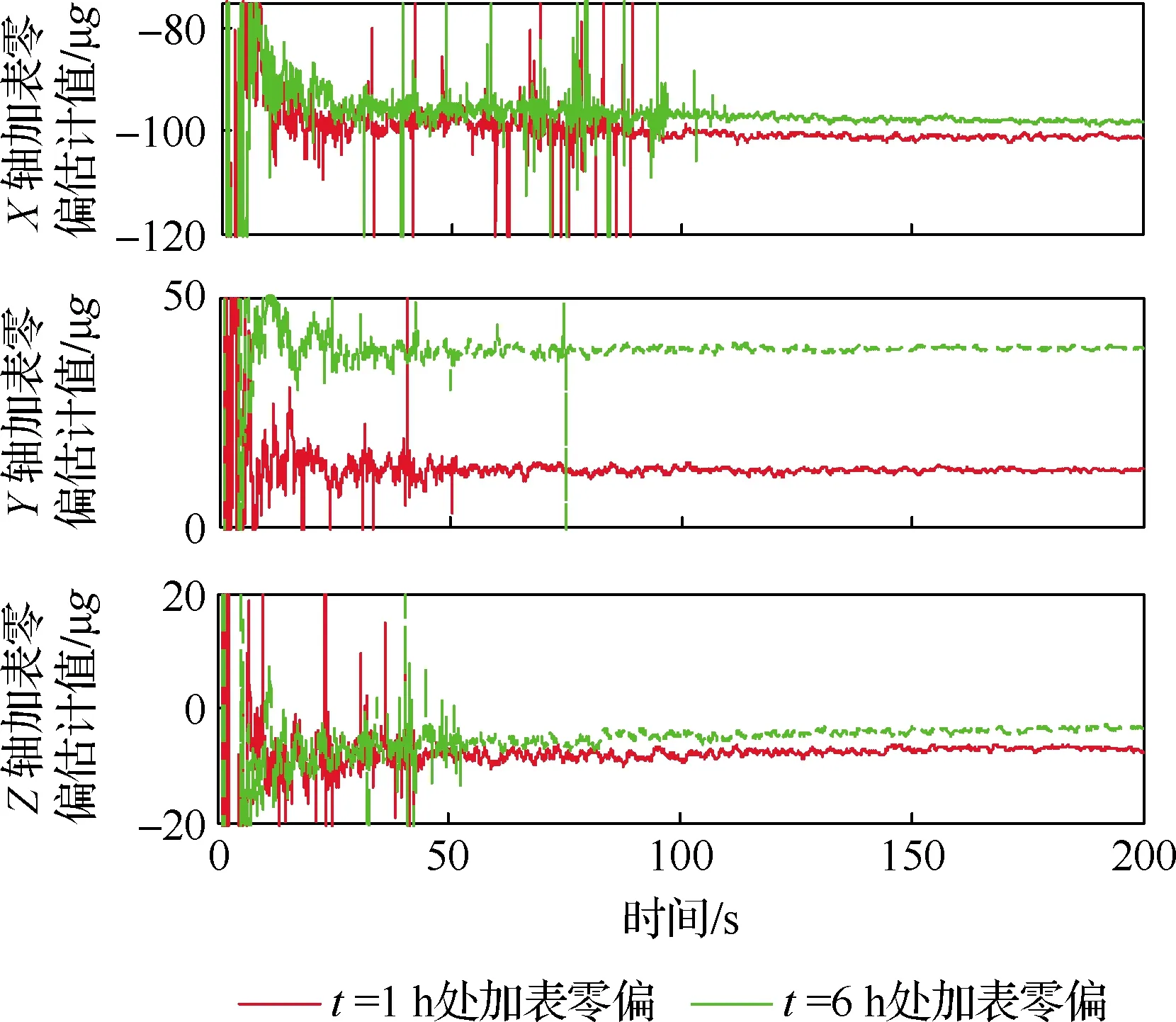
图10 t=1 h和t=6 h处3轴加速度计零偏估计值Fig.10 Estimations of three-axis accelerometer biases at t=1 h and t=6 h

t=6 h后4种方案导航误差的均方根统计值如表4所示。

图11和表4取得了与前述仿真测试一致的结果。方案2中仅补偿加速度计零偏仅能抑制由其造成的稳态误差，同时由方案2可以看到，仅补偿加速度计零偏无法抑制航向、速度及位置误差。相对于方案3，方案4由于在综合校正前补偿了加速度计零偏，取得了更高的陀螺漂移估计精度，因而最终得到了更好的导航误差抑制效果。方案4在10 min的DVL信息和两次间断的外部位置和航向信息辅助下，有效地估计并补偿了陀螺漂移，有效地提高了长航时格网惯导系统的导航精度。

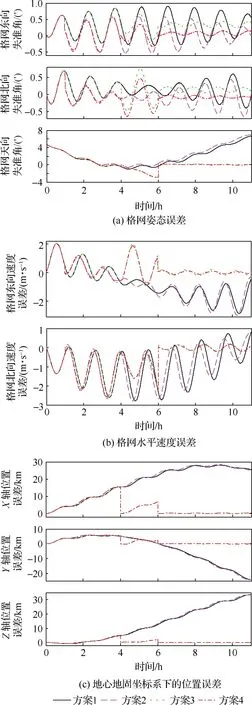
图11 地心地固坐标系下的位置误差Fig.11 Position errors in earth centered-earth fixed frame

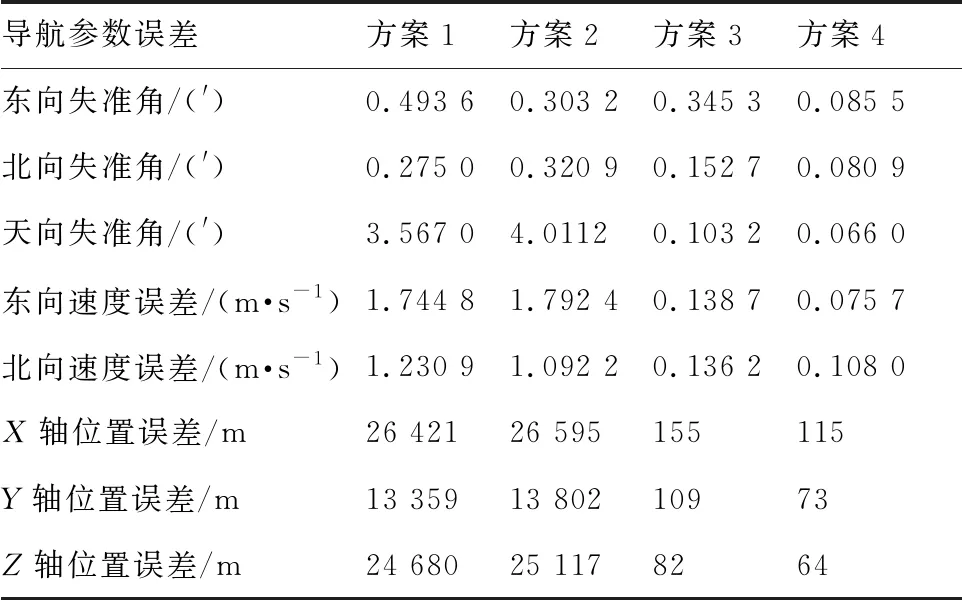
表4 t=6 h后4种方案导航误差的均方根统计值

针对本文所设计的综合校正方案，补充以下3点：① 针对适用于中低纬度地区的指北方位惯导系统，若能推导得到DVL辅助下的地理坐标系框架下的加速度计零偏和姿态的估计目标函数和适用于无阻尼综合校正的P方程，延续本文的综合校正方案设计思路，同样可以设计出适用于指北方位惯导系统的无阻尼两点式综合校正策略；② 为确保参数估计方法所估计出的加速度计零偏和姿态的准确性，本文所提出的综合校正方案需要保证DVL测速的准确性。在以下情况不采用DVL辅助估计相关参数：船舶进出港口靠离岸时、船舶转弯时、复杂恶劣海况条件下；③ 实际船用惯导系统在初始对准阶段可完成水平方向陀螺漂移的估计和补偿[24]。本文为凸显综合校正中陀螺漂移估计精度和导航误差抑制效果，并未在初始对准阶段实现陀螺漂移的估计和补偿。由于本文综合校正方案可准确估计出天向陀螺漂移，因而本文的综合校正方案在陀螺漂移估计和导航误差抑制方面仍然具备积极作用。

5 结 论

1) 采用本文所设计的格网坐标系框架下的参数估计方法在200 s时间内即可准确地估计出加速度计零偏和水平姿态，补偿加速度计零偏可有效地抑制格网INS中由加速度计零偏所造成的水平姿态误差。执行综合校正方案仅需10 min 的DVL辅助时间，相对于已有的研究，进一步地缩短了DVL的使用时间，提高了综合校正方案在实际应用中的普适性。

2) 加速度计零偏的补偿提高了陀螺漂移的估计精度。由于惯性器件测量误差补偿更加彻底，本文所设计的综合校正方案在抑制格网INS积累的导航误差方面效果更明显。实测条件下，相对于已有的综合校正方案，格网姿态误差分别减小75.2%、47.0%和36.0%；格网水平速度误差分别减小45.4%和20.7%；地心地固坐标系下位置误差分别减小25.8%、33.0%和22.0%。