一种适合迭代求解的反馈力浸入边界法
李旭,周洲,薛臣
西北工业大学 航空学院,西安 710072
工程实际中存在大量的流固耦合问题,物体存在复杂的运动或变形,这给数值求解带来了困难。传统的贴体网格方法已经实现了对此类问题的计算,如动网格方法、嵌套网格方法。但是这些方法都不可避免地需要网格的运动,这就带来了新的问题。当物体出现大变形或大位移时,动网格方法计算可能会出现负网格,而嵌套网格方法则容易出现孤儿网格[1],这都会影响计算的稳定性。
浸入边界法[2-3]采用笛卡尔网格进行计算,物面用一系列离散的Lagrange点表示,通过边界对周围流体网格施加力或直接施加速度边界条件来等效物体对流体的作用。在对运动边界进行计算时,只需要改变Lagrange点的作用区域,并不需要流体网格的运动,避免了传统贴体网格方法网格的变形或运动,不仅保证了网格质量,还降低了复杂几何的网格生成难度。经过多年的发展,目前已经出现了许多种不同形式[4-5]的浸入边界法。Goldstein的反馈力浸入边界法(又称虚拟边界法,Virtual Boundary Method)正是这些方法中的一种[6-7]。该方法基于非定常Navier-Stokes(N-S)方程提出,其吸取了控制理论中反馈的思想,分别采用积分和比例环节,利用物面的速度误差计算力源项,并利用力源不断对流场进行反馈,最终实现无滑移边界条件。该方法形式简单,不用对物体内外的流体网格单元进行区分,也不用对已有求解器进行大的改动,因此方便使用[8-9],已经成功应用到了柔性变形[10-12]、扑翼运动[13-15]、叶栅颤振[16-19]、多相流计算[19]等问题上。
Goldstein的反馈力浸入边界法含有对时间的积分项,这也是目前国内外学者将该方法与非定常N-S方程求解结合的原因之一。对控制方程的求解采用的方法包括谱方法[9]、投影法[15,20]、格子玻尔兹曼方法[21]等,多为显式时间推进。Goldstein的反馈力方法在应用时有两个不便:第一,积分和比例环节的反馈系数需要人为给定;第二,计算存在稳定性问题。原始的反馈力浸入边界法在进行显式计算时,出于稳定性的要求,求解方法有非常严格的时间步长限制[20,22]。显式计算本来就有稳定性要求,采用反馈力浸入边界法后,受反馈力系数取值的影响,计算的时间步将必须取得很小,不然会引起发散,这降低了求解的效率。文献[21]指出Lee研究了在采用反馈力浸入边界法时不同时间推进方法的稳定性范围,对比了Adams-Bashforth格式与Runge-Kutta格式的差异,结果表明Runge-Kutta类方法稳定性较强,但CFL(Courant-Friedrichs-Lewy)数仍不能超过1。Shoele和Zhu[12]将加权隐式Crank-Nicolson格式与反馈力浸入边界法结合,但反馈力源项仍然按照时间步进行更新,为保证格式的有界性,时间步长仍要受到限制。
由此可知,显式求解制约了反馈力浸入边界法发挥作用。与此相对,隐式方法通常是无条件稳定的,计算时可采用更大的时间步,更加适合实际的工程计算。因此,将隐式求解方法与反馈力浸入边界法结合是一种不错的选择。另外,对于一些不可压的定常流动,往往可直接利用松弛迭代方法对不含时间项的N-S方程进行求解,如果能将反馈力浸入边界法与这类定常求解方法结合,将进一步拓展该方法的使用范围,但目前还未见到这方面研究公开发表。
基于以上思考,本文对Goldstein的反馈力浸入边界法进行了改进,将原始方法中的时间积分项改为对迭代次数的求和。与原始方法相比,改进的方法不再含有与时间相关的参数。本文对一系列的定常与非定常算例进行了计算,结果表明改进后的方法可同时用于定常与非定常N-S方程的求解,这为以后反馈力浸入边界法的应用提供了新的选择。
1 数值计算方法
1.1 控制方程
非定常不可压的N-S方程组为
(1)
式中:ρ为密度;p为压力;μ为层流黏性系数;F(x,t)为流体的力源项,其计算公式为
(2)
其中:f(xs,t)为物体的力源项;δ(x-xs)为Delta函数[23],积分前的负号表示物体的力源与流体的力源方向相反。Goldestein的反馈力浸入边界法计算物体的力源项的表达式为
β′(u(x,t)-u(xs,t))
(3)
式中:u(x,t)为流体计算得到的物面速度,可通过Delta函数计算得到;u(xs,t)为物面真正的速度。式(3)含有两个待定参数:α′和β′,需要人为给定,控制原理如图1所示。

图1 反馈力浸入边界法原理Fig.1 Principle of feedback forcing immersed boundary method
图1中的比例积分环节代表式(3),通过每个时间步的速度误差反馈,使|u(x,t)-u(xs,t)|趋于0,从而实现无滑移边界条件。
Delta函数是物面节点与流场网格单元信息交流的关键,其形式并不唯一,本文选用的Delta函数为
δ(r)=
(4)
阻力系数的计算参考文献[20],表达式为
(5)
式中:右边第1项表示物面上力源的积分,S指物体表面,fx为反馈力法计算物面上一点x方向的动量源项;第2项反映运动加速度的效应,V表示物体的体积;uc,x表示物体质心平动速度在x方向的分量。同理可得物体其他方向的受力。本文所有算例的密度均取为ρ=1.0 kg/m3。需说明的是,本文在采用式(2)计算时,反馈力参数均取正值。
1.2 反馈力浸入边界法的改进
Goldstein的反馈力浸入边界法(后文统称原始方法)与显式求解方法结合将严重限制计算的效率,难以在工程应用中推广。而隐式格式通常没有稳定性的限制,将反馈力浸入边界法与隐式格式结合,是一种有效的解决办法,也能更好地发挥反馈力浸入边界法的优点,这正是本文改进方法的出发点。
在进行数值计算时,Goldstein反馈力的计算公式可写为
β′(u(x,t)-u(xs,t))
(6)
式中:i表示时间步数,t=N′·Δt,N′表示当前的时间步数。即式(3)中对时间的积分项化为了对时间步的求和。通过对不同时间步的速度误差进行反馈来最终满足物面边界条件,这是目前国内外学者计算时采用的通用方式。
从纯反馈的原理出发,通过对式(6)进行分析,本文认为既然α′和β′需要人为给定,可以对其重新进行定义,令α=α′·Δt,β=β′,则可得
β(u(x,N)-u(xs,N))
(7)
式中:N表示当前计算的迭代次数。式(7)不含时间相关的参数,积分环节转化为不同次迭代速度误差的求和,而非式(6)中不同时间步速度误差的求和,这是与原始方法最大的不同之处。相同的是,仍然是通过对流场速度误差的反馈来计算力源项。相比式(6),改进后的方法有两方面的好处:第一,由于不含时间相关参数,可直接与一些定常N-S方程迭代求解方法结合;第二,在非定常计算时,通过迭代次数来计算力源项更加适合隐式求解,因为隐式推进一个时间步内往往有多次迭代的要求。
进一步来看,方程求解的迭代过程就是流域内的网格单元速度不断调整,达到收敛,从而与给定边界条件相适应的过程,这正好与控制系统中的反馈作用相类似。当实际的输出量与给定值存在偏差时,系统就不断通过误差反馈来减小偏差,从而使得输出量等于给定值。也就是说,直接利用迭代过程中的速度误差来计算力源项,并将其反馈给流体以期实现无滑移边界条件是可行的,反馈原理的本质不应与N-S方程的具体求解方法有关。
因此,改进的方法将具有更大的适用性。本文改进的方法不仅能与含有时间项的N-S方程进行结合,还能与不含时间项的N-S方程进行迭代求解,本文将对这一观点进行验证。
Fluent是目前一款应用较广泛的CFD商业软件,其基于有限体积法,求解器分为两大类:密度基和压力基。密度基求解器定常与非定常计算均按照时间推进求解,压力基求解器则不同。对于定常计算,压力基求解器求解的是不含时间项的N-S方程,非定常计算才含有时间项,且为隐式时间推进[24]。本文选用压力基求解器,基于软件中的用户自定义函数(User-Defined Functions, UDFs),通过一系列定常与非定常算例的计算,验证本文改进反馈力浸入边界法的有效性。
各个算例空间离散均采用二阶精度。对于非定常计算,时间推进则采用一阶隐式。定常计算可直接根据迭代进行力源的更新。对于非定常隐式计算,改进方法的实施步骤如下:
步骤1初始化,读入物面Lagrange点坐标。
步骤2每个时间步开始,如果物面位置发生变化,则更新Lagrange点,并在本时间步的迭代过程中保持其坐标不变。根据迭代次数,利用改进方法进行力源项的更新,并将其添加到动量方程中,参与控制方程的求解。
步骤3待本时间步迭代收敛,利用最终的力源进行本时间步物体受力的计算。
步骤4重复步骤2和步骤3,进行下一时间步的计算。
反馈力源的计算在DEFINE_ADJUST宏中进行,并通过DEFINE_SOURCE宏将其加给动量方程。关于UDF更多的使用细节,可参考Fluent自带的UDF Manual进行了解。
2 改进反馈力浸入边界法的验证
2.1 静止圆柱绕流
对静止圆柱绕流的计算是验证数值方法的经典算例。首先,本文对雷诺数Re=40时静止圆柱的流动进行了计算,以此来验证本文改进的反馈力方法在定常N-S方程求解时的有效性。采用Fluent压力基求解器中两种不同的定常计算方法,控制方程求解均不含时间项,进行松弛迭代求解。此时由于计算不再是时间推进求解,Goldstein的原始公式不再适用。
圆柱表面均匀分布75个Lagrange点,所在流域采用均匀网格,网格间距Δx的选取采用文献[25]的方法,计算网格量为29 380。
如图2所示,计算源项时需要对网格单元进行搜索,为减少搜索的范围,流体网格被分成了内外两个域。圆柱阻力系数的定义为
(8)
式中:U∞为自由来流速度,U∞=5.84 m/s;D为圆柱直径,D=1×10-4m。采用矩形计算域,60D×40D。入口采用速度入口,出口采用压力出口,上下边界设置为对称边界条件,空间离散采用二阶精度。将分别基于Simplec和Couple算法对静止圆柱绕流进行计算。其中Simplec为分离式求解(经典的压力修正算法),Couple则为耦合式求解,以此来检验改进方法对不同求解格式的可靠性。

图2 计算网格分布Fig.2 Grid distribution in simulation
确定好网格和边界条件后,就需要对α和β进行取值。虽然反馈原理的本质不变,但α和β的取值会影响到反馈的效果。α和β选取过大,会引起计算振荡,甚至导致显式计算发散;选取过小,会使得收敛变慢[9]。正如前文所说,目前并没有理论的方法确定α和β的最优值,这与计算状态和求解器本身相关,本文选取的值也是经过尝试确定的。
本文研究了α和β的取值对计算结果的影响。由于物体静止,式(5)中的第2项为0。基于Simplec算法,对比不同反馈力参数对计算收敛的影响,结果如图3所示。
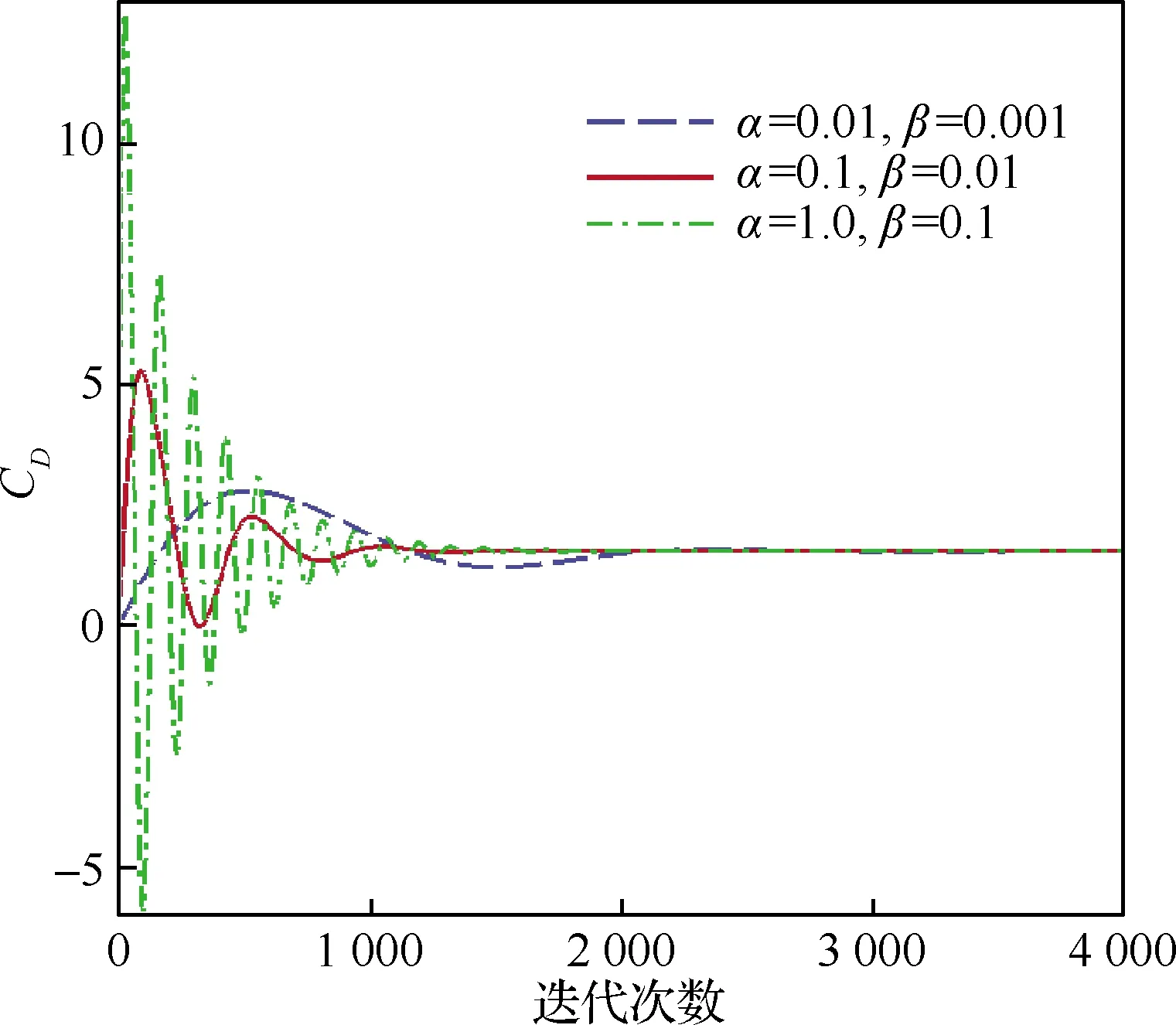
图3 反馈力参数对收敛的影响Fig.3 Influence of feedback forcing parameters for iteration
在3种不同取值下,阻力系数均收敛到了相同值。取α=1.0,β=0.1时,阻力系数的振荡比较明显,即超调量大;取α=0.01,β=0.001时,阻力系数波动幅值较小,但达到平稳速度较慢。因此,确定本算例反馈力参数α=0.1,β=0.01。
在计算过程中,每进行一次迭代,反馈力的源项都会得到更新,再将式(7)的力源分布到周围的流体网格上,进行下一次迭代,如此反复进行,直到计算收敛。
取Simplec计算收敛后流场的流线如图4所示。由于雷诺数较小,可以看出圆柱后方形成了两个对称、稳定的分离涡。表1是计算得到的圆柱绕流特征参数(阻力系数CD和无量纲回流区长度L/D),分别是两种求解方法与改进的反馈力浸入边界法结合(表中用Simplec和Couple表示),并与文献[26-28]的结果对比。通过圆柱绕流特征参数的对比可知,本文计算得到的圆柱阻力系数和回流区的长度与文献符合较好。
再取圆柱表面的压力系数Cp与文献[29]对比,如图5所示。可以看出,本文改进方法计算的压力系数与文献[29]给出的计算结果符合很好,表明本文改进的反馈力浸入边界法是有效的。不同于原始方法,本文改进的方法能用于不含时间项N-S方程的迭代求解,且反馈力系数取值对收敛结果没有大的影响。由于Simplec计算求解速度快,本文以后的计算均采用Simplec算法。
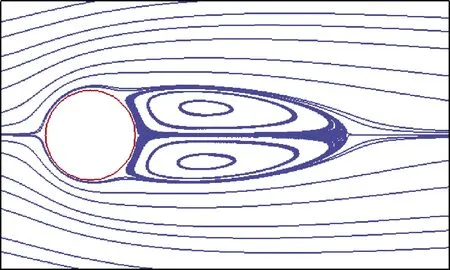
图4 圆柱流线(Re=40)Fig.4 Streamlines on circular cylinder at Re=40

表1 Re=40阻力系数和回流区长度对比

图5 静止圆柱压力系数Fig.5 Pressure coefficient for stationary circular cylinder
以上计算求解的是不含时间项的N-S方程,为验证改进方法在非定常隐式求解上的有效性,本文对Re=40时的圆柱绕流进行了非定常模拟。同样基于Simplec算法,对含有时间项的N-S方程进行求解,对原始反馈力浸入边界法与改进方法的收敛效果进行对比。
在进行隐式计算时,原始方法的源项是按照时间步进行计算的,则每个时间步只在最开始进行更新,一个时间步内其值保持不变。本文改进方法的源项基于迭代次数计算,每一次迭代后源项均会得到修正,一个时间步内其值一般是变化的。
时间步长取为0.002 s,一个时间步内迭代20次,采用相同的计算设置,对两种方法的收敛特性进行对比。图6为阻力系数的收敛曲线。可以看出,采用原始方法进行隐式计算时收敛较慢,特别是在快接近稳定值的时候,最终到500个时间步才完全收敛。而本文改进的方法则很快收敛,阻力在100个时间步后就达到平稳。
参考文献[14],定义CFL数为
式中:Δx=2.96×10-6m,为圆柱周围Euler网格尺寸。本文改进方法隐式计算与文献显式结果对比如表2所示。由于本文是隐式求解,与显式计算[8, 14]相比,CFL数可以取的很大,这也体现了隐式求解的好处。
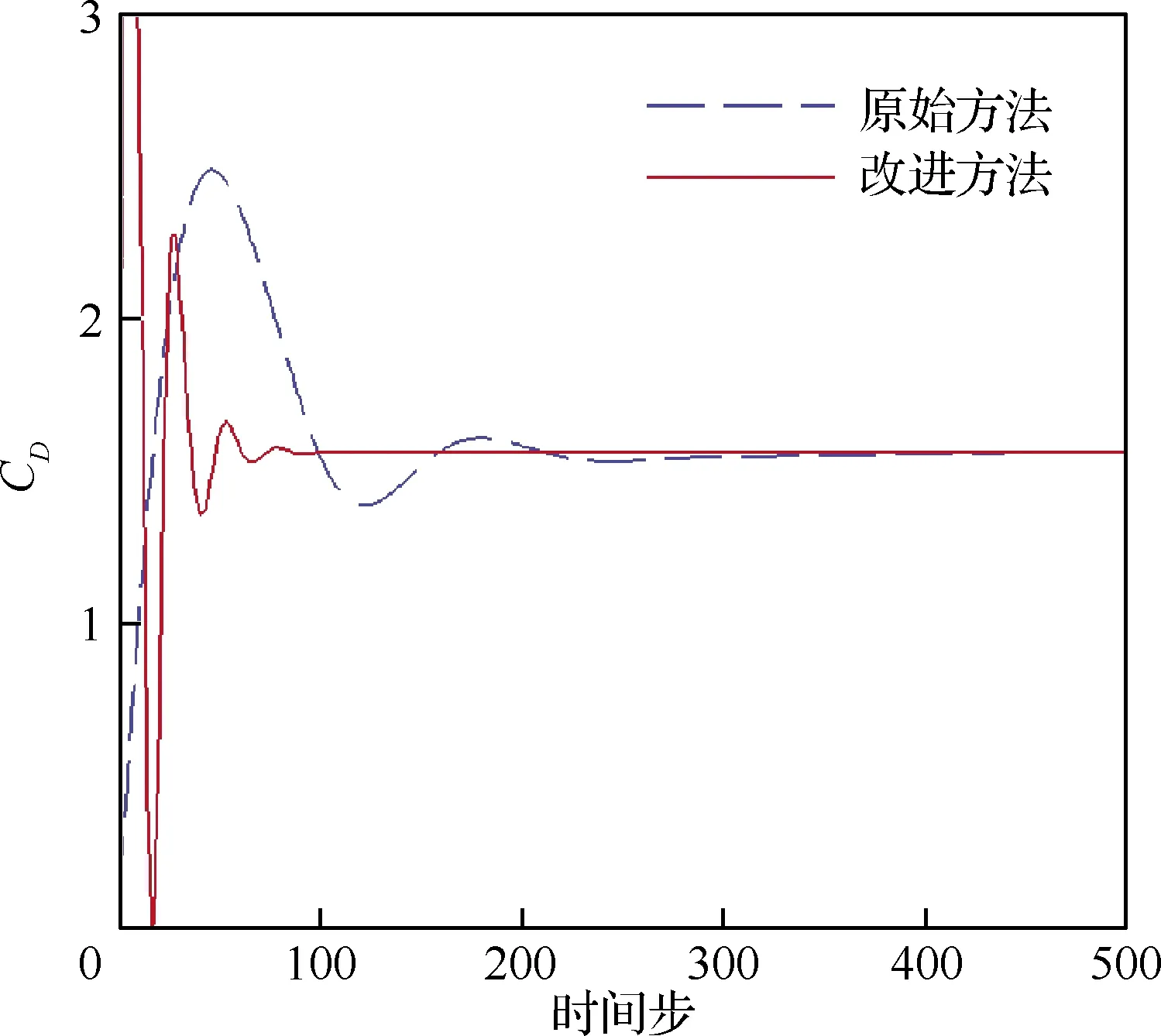
图6 静止边界隐式计算收敛效率对比Fig.6 Comparison of efficiency for implicit iterations at stationary boundary
从数值求解上来看,在代数方程求解的过程中,源项影响的是方程组的常数项。隐式求解每一次迭代都修正源项,使得源项与速度场的同步性得到改善,能起到加速收敛的作用。也就是说,改进的方法更加适合非定常隐式求解。

表2 Re=40时隐式与显式结果对比
2.2 振荡圆柱
为验证改进方法对运动边界模拟的可行性,选取静止流体中往复振动的圆柱[29-30]进行非定常计算,采用Simplec算法求解不可压非定常N-S方程,通过与文献对比来验证本文方法在运动物体求解上的有效性。
本算例计算域的大小取为40D×40D,圆柱将在水平方向进行往复运动,平衡位置在原点处,运动方程为
x(t)=-Asin(2πft)
(9)
式中:x为圆柱水平方向位移;A为振动幅值;f为振动频率。
在本算例中,影响计算结果的关键参数为雷诺数Re和KC(Keulegan-Carpenter)数,分别定义为
(10)
式中:umax为圆柱振动的最大速度,umax=2πfA。本文选取Re=100,KC=5。
参考文献[8],四周远场边界设置为无剪切的物面条件。由于采用隐式计算,一个周期只取360个时间步,每个时间步内迭代次数为20次。反馈力参数取值见表3。
对于圆柱表面运动速度的计算,可直接对式(9) 求导获得,然后将该速度代入式(7)中进行力源项的计算。在一个时间步内,圆柱的位置不会变化,每迭代一次,流场速度得到更新,反馈力

表3 不同算例反馈力参数Table 3 Feedback parameters for different cases
源项就会进行更新,然后再将其添加到动量方程中,进行下一次迭代,直到该时间步收敛。
与2.1节相同,流场网格分为了两个域,内区域网格量为40 000,圆柱运动过程都在其中,外区域网格量为31 824,总计网格为71 824,物面有75个Lagrange点。在计算过程中,只对圆柱所在区域的网格进行搜索判断以及反馈力源项的赋值。运动稳定后,得到流场不同时刻的压力及涡量如图7所示。
图7中涡量的正负分别用虚线和实线表示,当圆柱向远离平衡位置方向运动时,其后会形成两个强度相同、方向相反的对称涡;而当圆柱向平衡位置返回时,其将分开之前形成的这对涡,并改变涡的旋转方向,这种现象与文献[30]一致。

图7 不同相位下的涡量/压力等值线Fig.7 Vorticity/pressure contours at different phase angles
取改进方法计算的圆柱一个周期的阻力曲线与文献进行对比,如图9所示。可以看出,阻力的最大、最小值并不是在特殊相位(t=0.25nT,n为正整数,T为振动周期)时取得,这与圆柱运动过程中流体的惯性有关,表现出了迟滞特性,计算得到的振动圆柱阻力的变化与文献[30]符合较好。

图8 运动边界隐式计算效率对比Fig.8 Comparison of efficiency for implicit iterations at moving boundary
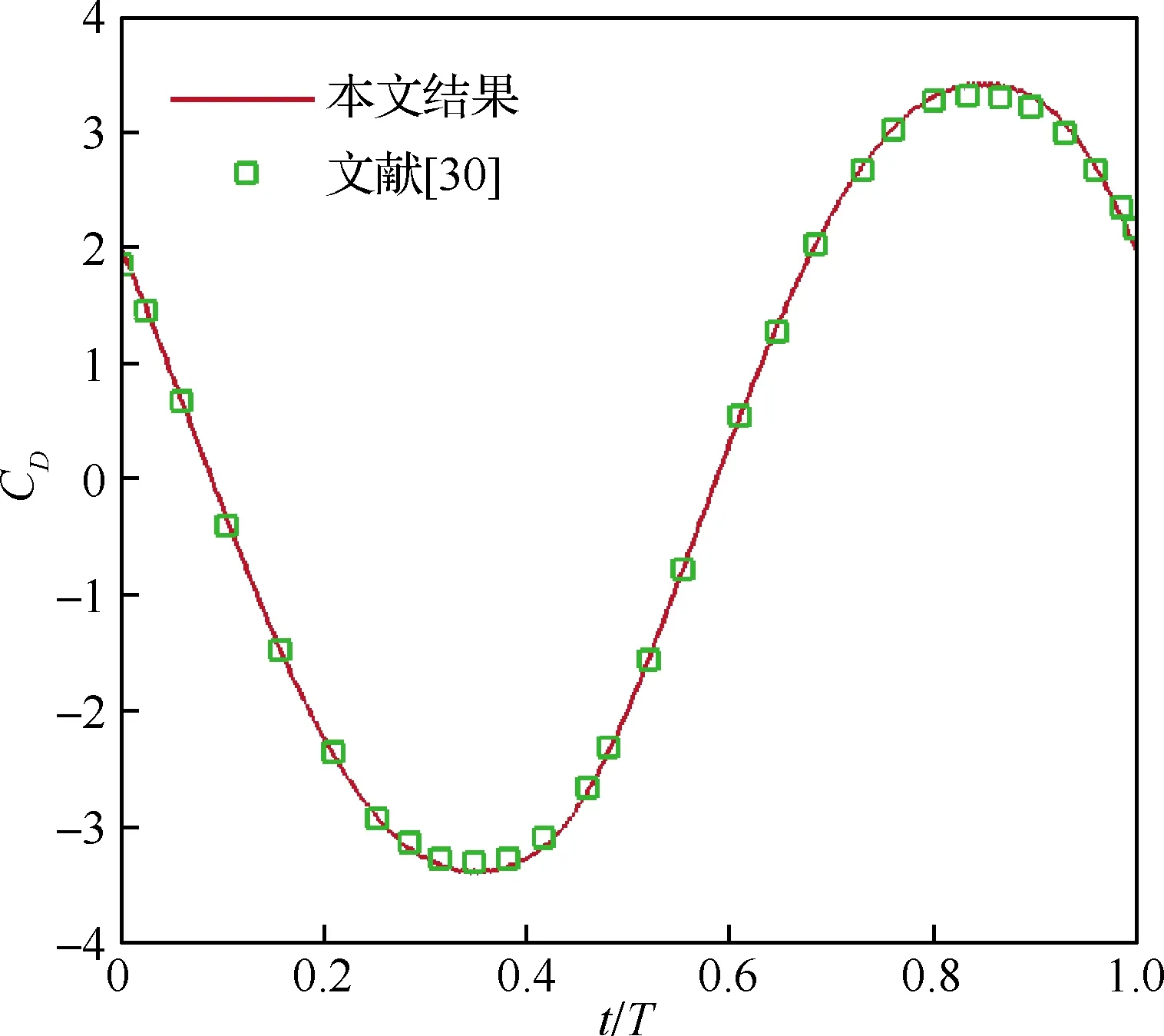
图9 阻力系数变化曲线Fig.9 Time history of drag coefficient
以上结果表明本文改进的反馈力浸入边界法可与隐式求解方法结合,对运动物体进行迭代计算,且收敛效果优于原始方法。
2.3 运动椭圆翼
振动圆柱只有一个方向的运动,椭圆翼的运动要更加复杂,其不仅有平动,还有绕自身质心的转动,可用其来研究昆虫翅膀运动时非定常流动机理[31]。本节将选取静止流体中的椭圆翼来验证本文改进方法对物体复杂运动的模拟能力。
椭圆翼运动如图10[31]所示,质心的平动和绕质心的转动规律为
(11)
(12)

阻力系数和升力系数的定义分别为
(13)

图10 椭圆翼运动路径[31]Fig.10 Flapping path of ellipse wing[31]
式中:c为椭圆翼的长轴长,取c=1 m。椭圆翼的短轴长b=0.25 m。一个周期T分为360个时间步,内迭代次数为20。选取计算域为80c×80c,四周远场边界采用无剪切壁面,总网格量为164 160。由于运动比较复杂,物面取150个Lagrange点。
计算稳定后,得到椭圆翼运动周期内不同时刻的涡量图如图11所示。在向下运动过程中,椭圆翼前后缘会产生一对反向旋转的涡(t=0.25T),由于椭圆翼自身的旋转作用,这对涡将逐渐靠近(t=0.44T)。在向上扑动过程中,之前形成的这对涡会从椭圆翼表面脱落(t=0.74T),形成一对相互作用的偶极子,并向下运动(t=0.99T)。
得到椭圆翼的阻力和升力变化规律如图12所示。可以看出,由于椭圆翼流场非定常特性明显,其气动力变化并不是简单的正弦曲线。另外,本文计算的椭圆翼的升力阻力变化与文献[14]基本一致,且相比文献[14],计算没有明显的数值振荡,表明可以利用本文改进的方法进行隐式计算,对复杂的非定常运动进行模拟。
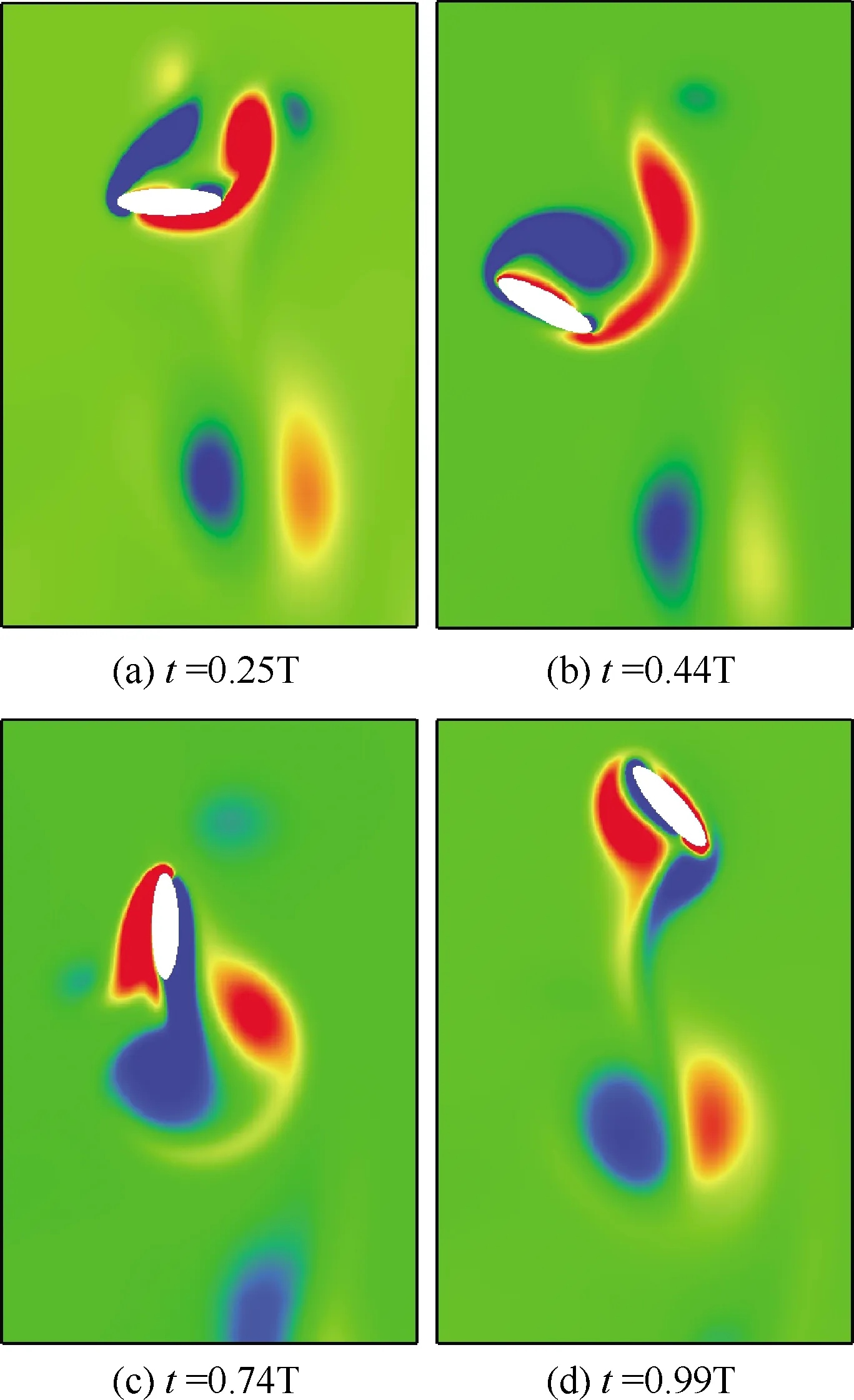
图11 一个周期内不同时刻的涡量图Fig.11 Vorticity fields during one period

图12 扑动过程中的气动力曲线Fig.12 Curves of aerodynamic coefficients during flapping
2.4 静止圆球
为进一步验证本文方法对三维物体模拟的可靠性,选取静止圆球进行定常计算,求解不含时间项的N-S方程。采用Simplec算法,计算域大小为80D×60D×60D,D=0.001 m。
为减少网格量,本文在圆球所处的流域进行了局部网格加密,如图13所示,加密后总的网格量为282万。远场边界分别采用速度入口和压力出口。
圆球表面的网格如图14所示,采用三角形单元来离散球面,共计有3 860个单元。来流速度分别取15 m/s和25 m/s,对Re=150和Re=250时的圆球绕流进行计算,得到流场如图15所示。可以看出,在Re=150时,绕圆球的流动是轴对称的。但在Re=250时,虽然圆球本身是轴对称的,但流动的对称性减弱,x-y面的流动和x-z面的流动存在差异,流场只存在面对称,即上下对称。由于x-z面涡不对称,圆球产生了侧力,但流动依旧保持稳态。

图13 局部网格加密Fig.13 Local refining for computation mesh
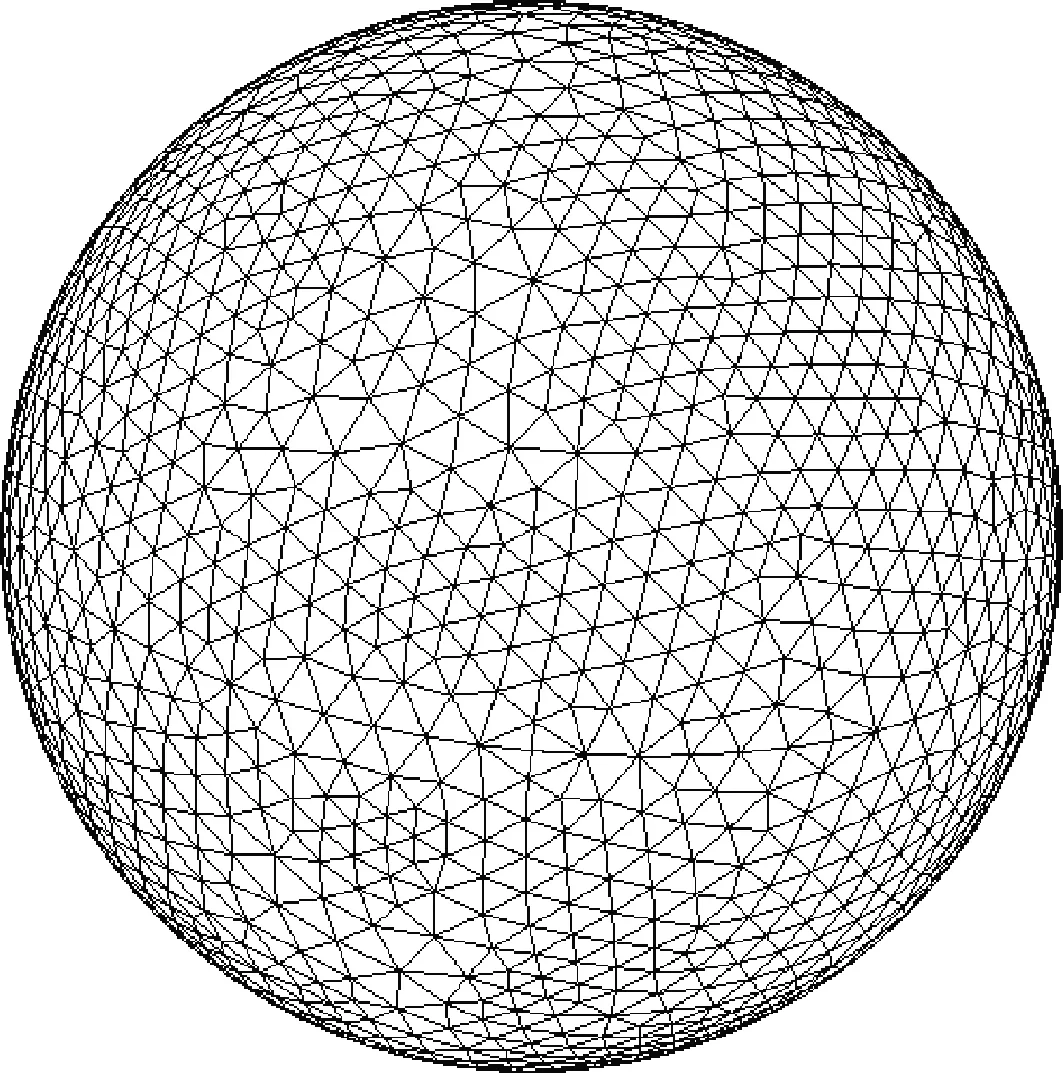
图14 圆球表面的Lagrange网格单元Fig.14 Lagrange mesh of sphere surface
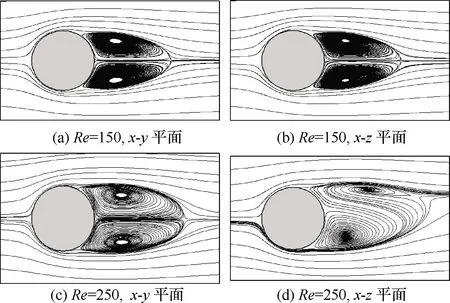
图15 不同雷诺数圆球绕流流线Fig.15 Streamlines for flow past sphere at different Re
本文计算得到圆球的受力与文献对比如表4所示。可以看出,本文计算结果与文献结果符合较好,在Re=250时,圆球产生了侧力(表中用Cc表示)。表明本文改进的反馈力浸入边界方法适合三维物体的计算。
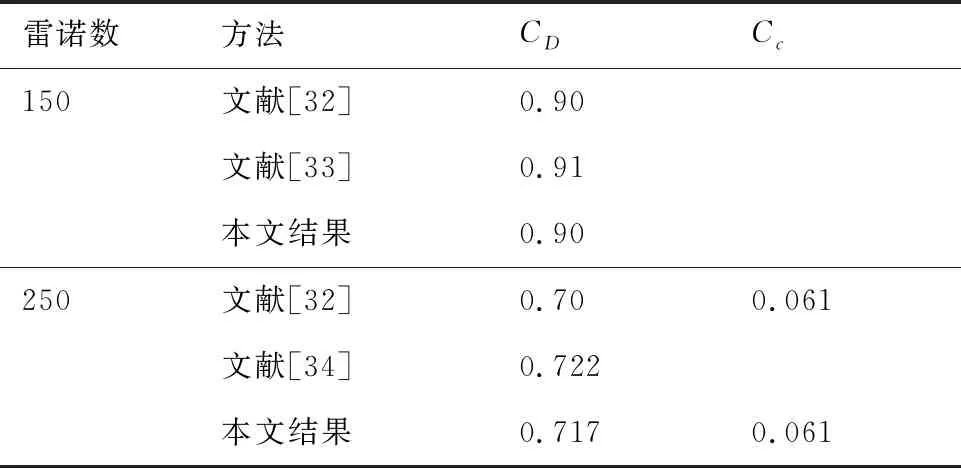
表4 圆球气动特性对比
3 结 论
本文对Goldstein的反馈力浸入边界法进行了研究和改进,将原始方法中含有的对速度误差的时间积分转化为迭代过程中速度误差的求和,利用多个定常与非定常算例验证了改进方法的有效性。得到的主要结论有:
1) 可直接基于迭代次数对反馈力源项进行计算。与原始方法相比,由于不含时间相关参数,改进的反馈力浸入边界法可与求解定常N-S方程的松弛迭代方法结合,用于定常流动计算。
2) 隐式时间推进可以避免反馈力浸入边界法显式求解时严格的时间步长限制。本文改进的反馈力浸入边界法适合于隐式时间推进,可实现对非定常N-S方程的求解,且收敛特性要优于原始方法。
3) 改进的方法与原始方法均是基于速度误差反馈的思想求解力源项,但本文改进的反馈力浸入边界法有更广泛的适用性。

