求解极值点偏移问题的一种技法

浙江省安吉县高级中学 (313300) 黄德丽

1.问题提出

极值点(或零点)偏移问题是近年各地模拟试题的一个热点问题，其最早出现在2010年的全国卷和天津卷中，以考察学生是否具备一定的对称式构造能力，是以解决变量间的相互关系为主的一种数学模型问题．

引例已知函数f(x)=xe-x，若f(x1)=f(x2)，且x1≠x2，证明：x1+x2>2.

思考：在上述证明过程中，我们体会到了极值点的偏移，运用导数工具证出函数在某一区间上单调，从而得出结论．

尽管这种证明方式可以总结为一种模式加以理解和掌握，但处理起来仍然显得繁琐(通法往往如此)，特别是证明构造出来的新函数的单调性尤为如此，那么我们在深层挖掘题目内涵的基础上，能不能找到一种更为简捷的证明方法呢？

2.技法引入

从已经学习过基本不等式，可获取以下重要结论：当a,b为正实数时，则有

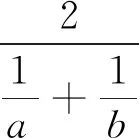
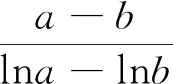
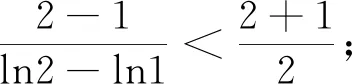
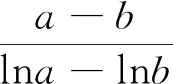
3.回眸一望

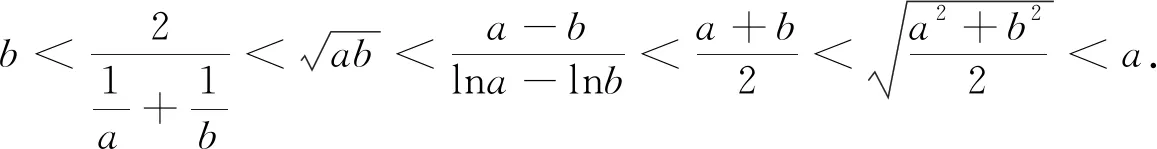
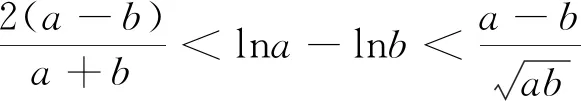
实际上，巧妙地利用对数均值不等式证明某些不等式确实会显得比较简便，往往比利用极值点(或零点)偏移思想证明不等式要简便很多．

4.再战江湖

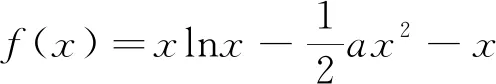
(1)求实数a的取值范围；

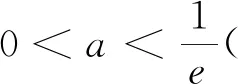
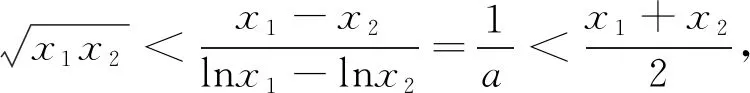
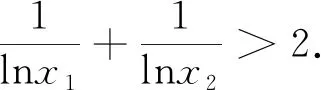
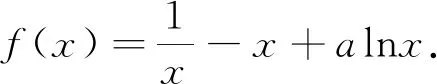
(1)讨论f(x)的单调性；

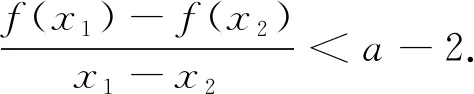
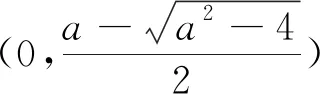
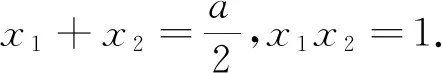
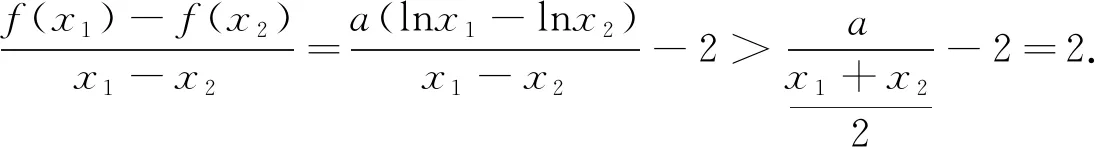
5.一夜春来

本文从与众不同的视角，围绕对数均值不等式结论的探究、证明及运用，有意回避了利用零点偏移或极值点偏移的思想证明类似不等式组，对于极值点偏移类问题的理解与分析将会大大深入，从另一方面我们也有效地拓展了基本不等式链，这对不等式知识也是一种加强，特别是在处理某些不等关系时在方法选择上又有了一个新台阶，并提供了一种全新的思路．这恰有一种“忽如一夜春风来，千树万树梨花开”的感觉．