一道印度奥林匹克不等式题的再推广
2020-12-01 09:20:10江苏省姜堰中等专业学校225500包长海
中学数学研究(江西) 2020年8期
江苏省姜堰中等专业学校 (225500) 包长海 陈 宇
1.原题呈现

2.拓展研究
笔者再将其推广如下结果:

证明:由题设可知s>0,s2=(a+b+c)2≥3(ab+bc+ca).由(λ+mb)(μ+a)+(λ+mc)(μ+b)+(λ+ma)(μ+c)=3λμ+sλ+msμ+m(ab+bc+ca);
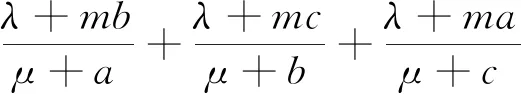
要证(3)式成立,只需证(4)式右端项与(3)式右端项的差大于0即可.
又因为(9λ2+6msλ+m2s2)(6μ+ms)-[3λμ+sλ+msμ+m(ab+bc+ca)](18λ+6ms)=9msλ2+6m2s2λ+m3s3-6ms2λ-18sλ2-18mλ(ab+bc+ca)-6m2s(ab+bc+ca)=9sλ2(m-2)+3ms2λ(m-2)+3mλ[ms2-6(ab+bc+ca)]+m2s[ms2-6(ab+bc+ca)]≥(3mλ+m2s)[2s2-6(ab+bc+ca)]≥0(∵m≥2).从而(3)成立得证.
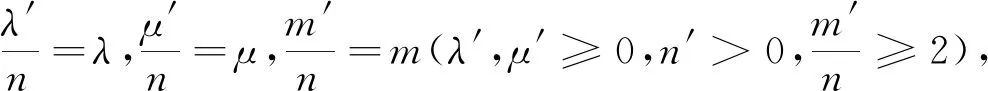
猜你喜欢
江苏农村经济(2023年8期)2023-09-13 06:35:08
数理化解题研究(2022年22期)2022-08-30 06:37:58
中小学校长(2021年9期)2021-10-14 14:36:12
河北理科教学研究(2021年1期)2021-06-07 07:49:14
江苏安全生产(2020年3期)2020-04-21 05:44:12
小读者(2019年24期)2020-01-19 01:51:48
新高考·高二数学(2018年1期)2018-11-20 02:15:42
党的生活(黑龙江)(2017年7期)2017-07-19 06:37:29
晚报文萃·开心版(2013年8期)2013-04-29 01:52:56
老年世界(2011年2期)2011-04-06 10:04:00

