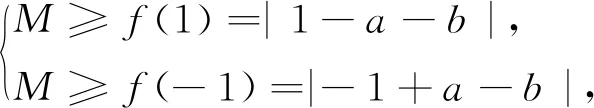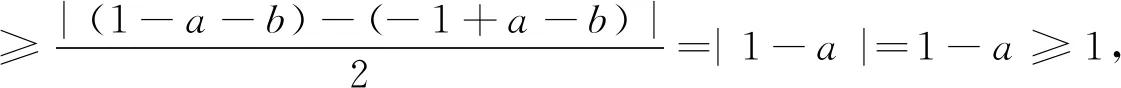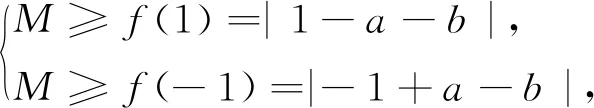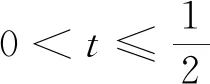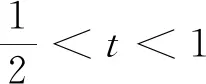一类双重最值问题的解法探究

江苏省海门中学 (226100) 杨智慧

双重最值问题是指形如求解min{max{f1(x)，f2(x)}}的相关问题,探究复杂的多元双重最值问题的解题策略，包括数形结合与分段(分类)讨论；探究了均值不等式、设而不求、先猜后证、绝对值的三角不等式放缩等方法，旨在介绍解决双重最值问题的通性通法.

引题已知函数f(x)=|x2-ax-b|,当x∈[-2,2]时设f(x)的最大值为M(a,b)，则M(a,b)的最小值为，此时a+b=.

解析:利用几何意义解之，这里的M(a,b)可以理解为函数y=x2,x∈[-2,2]和直线y=ax+b的铅垂距离的最大值，由于a,b没有限制，所以需要考虑任意直线.

易知，在斜率存在情况下，M的值总不小于2，当斜率为0时，我们发现M有最小值可以为2，由于a,b没有限定，所以我们可以令a=0,b=2，此时M(a,b)的最小值为2.

问题设函数f(x)=|x3-ax-b|，x∈[-1,1]，其中a、b∈R.若f(x)≤M恒成立，则当M取得最小值时，a+b的值为.

方法一：分类讨论，利用绝对值三角不等式

构造函数g(x)=x3-ax-b，可知该函数关于点(0,-b)对称，然后分a≤0、a≥3、0

详解:构造函数g(x)=x3-ax-b，则f(x)=|g(x)|，由于g(x)+g(-x)=(x3-ax-b)+

(-x3+ax-b)=-2b，所以函数y=g(x)的图象关于点(0,-b)对称，且g′(x)=3x2-a.

①当a≤0时，g′(x)≥0，函数y=g(x)在区间[-1,1]上单调递增，则

②当a≥3时，对任意的x∈[-1,1]，g′(x)≤0，函数y=g(x)在区间[-1,1]上单调递减，则

x[-1,-t)-t(-t,t)t(t,1]g'(x)+0-0+g(x)↗极大值↘极小值↗

评注：本题考查利用绝对值三次函数的最值求参数，解题的关键就是充分利用三次函数的单调性，找出绝对值三次函数最大值的可能值，并结合绝对值三角不等式的性质来求解，考查分析问题和解决问题的能力，属于难题.

方法二：寻求关键点，利用绝对值三角不等式放缩

方法三：利用函数奇偶性，消参处理恒等式

方法四：利用三倍角公式，巧妙进行三角换元

因为|cos3θ|=|4cos3θ-3cosθ|≤1，所以

方法五：数形结合，借助切比雪夫最佳逼近理论背景

图1

变式训练：设函数f(x)=(x-1)3-ax-b，x∈R，其中a，b∈R.

(Ⅰ)求f(x)的单调区间；

(Ⅱ)若f(x)存在极值点x0，且f(x1)=f(x0)，其中x1≠x0，求证：x1+2x0=3；

第(Ⅲ)问详解：设g(x)在区间[0,2]上的最大值为M，max{x,y}表示x,y两数的最大值.

下面分三种情况处理：

b|,|1-2a-b|}=max{|1-a+(a+b)|,