最大度较小的图的线性着色
彩春丽,易 华
最大度较小的图的线性着色
*彩春丽,易 华
(井冈山大学数理学院,江西,吉安 343009)
本文研究了最大度较小的图的线性着色问题。通过分析未着色顶点的邻近顶点的着色情况,扩充图的部分线性着色,利用数学归纳法证明了△() ≤ 4的非4正则图的线性色数有lc() ≤ 7和△() ≤ 5的非5正则图的线性色数有lc() ≤ 13。
最大度;线性着色;线性色数
0 引言
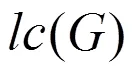
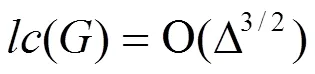
1 符号说明
2 主要结果

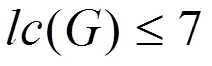


[1] Yuster R. Linear coloring of graphs [J].Discrete Mathematics, 1998, 185:293-297.
[2] Esperet L, Montassier M, Raspaud A. Linear choosability of graphs [J].Discrete Mathematics, 2008, 308:3938-3950.
[3] Cai C L, Xie D Z, Yang W J. A result on linear coloring of planar graphs[J]. Information Processing Letters, 2012, 112(22): 880-884.
[4] Liu C H, Yu G. Linear colorings of subcubic graphs[J]. European Journal of Combinatorics, 2013, 34: 1040-1050.
[5] Li C, Wang W, Raspaud A. Upper bounds on the linear chromatic number of a graph [J]. Discrete Mathematics, 2011, 311:232-238.
[6] Dong W, Lin W S. On linear coloring of planar graphs with small girth[J]. Discrete Applied Mathematics, 2014, 173: 35-44.
[7] Wang Y Q, Wu Q. Linear coloring of sparse graphs[J]. Discrete Applied Mathematics, 2012, 160: 664-772.
[8] Wang W F, Wang Y Q. Linear coloring of planar graphs without 4-cycles[J]. Graphs and Combinatorics, 2013, 29: 1113-1124.
LINEAR COLORING OF GRAPHS WITH SMALL MAXIMUM DEGREE
CAI Chun-li, YI Hua
(School of Mathematics and Physics, Jinggangshan University, Ji’an Jiangxi 343009, China)

maximum degree; linear coloring; linear chromatic number
O157.5
A
10.3969/j.issn.1674-8085.2020.05.002
1674-8085(2020)05-0005-05
2020-04-20;
2020-05-18
*彩春丽(1986-),女,河南商丘人,助教,硕士,主要从事图论及其应用研究(Email:619662208@qq.com);
易 华(1973-),男,湖北松滋人,讲师,博士,主要从事小波分析及其应用研究(Email:876145777@qq.com).

