含参广义向量拟均衡问题有效解映射的下半连续性
孟旭东
含参广义向量拟均衡问题有效解映射的下半连续性
孟旭东
(南昌航空大学科技学院,江西,南昌 330034)
针对一类含参广义向量拟均衡问题,在实Hausdorff拓扑向量空间中研究了有效解映射的下半连续性。在锥凹、一致连续及Hausdorff上半连续的假设下,运用分析的方法,得到了含参广义向量拟均衡问题有效解映射下半连续性定理。
有效解映射;下半连续性;含参广义向量拟均衡问题
向量优化、向量变分不等式、向量Nash平衡及向量补问题等均是向量均衡问题研究的热点问题。文献[1-3]主要讨论了向量均衡问题解的存在性。文献[4-13]重点围绕向量均衡问题解的稳定性进行分析,主要研究了解映射的下半连续性。文献[4-11]运用标量化方法、稠密性结果、凸分析及光滑分析等研究了含参(集值)向量均衡问题各种有效解映射的下半连续性。在锥凹及一致连续的条件下,Rabian,Panatda和Pakkapon在文献[12]中,运用标量化方法,讨论了含参广义向量均衡问题近似解映射的下半连续性。在文献[13]中,Han和Gong得到了含参广义强向量均衡问题有效解映射下半连续性定理。
受文献[12]与文献[13]思想的启发,在实Hausdorff拓扑向量空间中,研究含参广义向量拟均衡问题的有效解映射的下半连续性。通过转化为集值映射在零点下半连续的方法,给出含参广义向量拟均衡问题有效解映射下半连续的最优性条件。
1 预备知识

其中
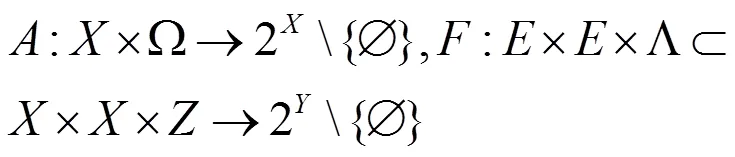
为给定集值映射,满足



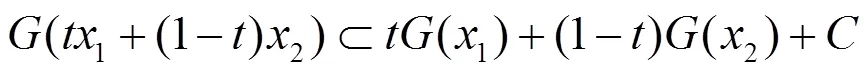



2 主要结果
定理 假设以下条件成立:




2.3 不同ADC值下肺结节良恶性分布情况 以ADC=1.41×10-3m2/s为临界值分析肺结节良恶性分布情况,结果显示,ADC<1.41×103 m2/s恶性病变的发生例数明显高于良性病变,而ADC≥1.41×103 m2/s的良性病变的发生例数明显高于恶性病变,见表3。


及
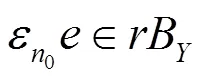



再由(5)知,


设
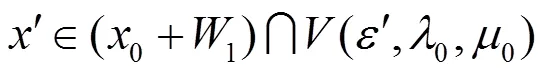




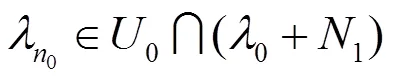
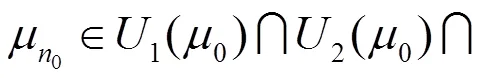
再由(12)与(13)知,

且

取
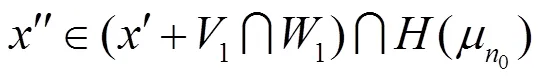

再由(10)知,

再由(2)、(9)与(16)知,

[1] Fu J F.Vector equilibrium problems,existence theroems and convexity of solutionset[J].J Glob Optim,2005, 31(1):109-119.
[2] Song W. Vector equilibrium problems with set-valued mapping[A]. In:Giannessi F. Variational inequalities and vector equilibia[C]. Dordrecht, Netherlands Kluwer, 2000, 38(2):403-418.
[3] Ansari Q H,Oettli W,Schlaer D.Generalization of vector equilibria[J].Math Meth Oper Res,1997,46(2): 147-152.
[4] Huang N J, Li J, Thompson H B. Stability for parametric implicit vector equilibrium problems[J]. Math Comput Model, 2006, 43(11): 1267-1274.
[5] Gong X H, Yao J C. Lower semicontinuity of the set of efficient solutions for generalized systems[J]. J Optim Theory Appl.,2008, 138(2):197-205.
[6] Chen C R, Li S J, Teo K L. Solution semicontinuity of parametric generalized vector equilibrium problems[J]. J Glob Optim, 2009, 45(2):309-318.
[7] Chen B, Gong X H. Continuity of the solution set to parametric set-valued weak vector equilibrium problems [J]. Pacific J Optim, 2010, 6(4): 511-520.
[8] Chen C R, Li S J. On the solution continuity of parametric generalized systems[J].Pacific J Optim. 2010, 6(1): 141-151.
[9] Peng Z Y, Chang S S. On the lower semicontinuity of the set of efficient solutions to parametric generalized systems[J].Optim Lett, 2014, 8(1):159-169.
[10] Peng Z Y,Lin Z,Yu K Z,et al.A note on solution lower semicontinuity for parametric generalized vector equilibrium problems[J].Journal of Inequalities and Applications,2014,2014(1):1-10.
[11] Li S J,Liu H M,Zhang Y, et al. Continuity of the solution mappings to parametric generalized strong vector equilibrium problems[J].J Glob Optim,2013, 55(17):597-610.
[12] Rabian W, Panatda B, Pakkapon P. Lower semicontinuity of approximate solution mappings to parametric generalized vector equilibrium problems[J]. Journal of Inequalities and Applications,2014, 2014(1):1-9.
[13] Han Y,Gong X H. Lower semicontinuity of solution mapping to parametric generalized strong vector equilibrium problems[J].Appl Math Lett.,2014,28(2): 38-41.
[14] Fu J Y.Generalized vector quasi-equilibrium problems[J]. Math Methods Oper Res.,2000,52(1): 57-64.
[15] Aubin J P, Ekeland I. Applied Nonlinear Analysis[M]. New York: Viley, 1984.
LOWER SEMI-CONTIONUITY OF EFFICIENT SOLUTION MAPPING TO PARAMETRIC GENERALIZED VECTOR QUASI-EQUILIBRIUM PROBLEMS
MENG Xu-dong
(Science College of Nanchang Hang kong University,Nanchang, Jiangxi, 330034,China)
The lower semi-continuity of efficient solution mapping to a class of parametric generalized vector quasi-equilibrium problems in real Hausdorff topological vector space is studied.Under the assumption conditions of cone concave,uniformly continuous and Hausdorff upper semi-continuous, the lower semi-continuity theorem for efficient solution mapping to the parametric generalized vector quasi-equilibrium problems is gained by using the method of analysis.
efficient solution mapping; lower semicontionuity; parametric generalized vector quasi-equilibrium problems
O317
A
10.3969/j.issn.1674-8085.2020.05.001
1674-8085(2020)05-0001-04
2020-05-08;
2020-06-15
国家自然科学基金项目(11201216);江西省教育厅科学技术重点研究项目(GJJ181565,GJJ191614);江西省教育厅科学技术研究项目(GJJ161597)
孟旭东(1982-),男,江西南昌人,副教授,硕士,主要从事向量均衡与向量优化理论研究(E-mail: mxudongm@163.com).

