基于动态R-Vine Copula的银行股指投资组合及风险度量研究

徐刚刚，狄千姿，石 慧

基于动态R-Vine Copula的银行股指投资组合及风险度量研究

*徐刚刚，狄千姿，石 慧

(新疆农业大学数理学院，新疆，乌鲁木齐 830052)

金融资产价格之间的波动往往具有结构相依性。为了研究银行股指数据间这种复杂关系，能够进一步准确度量金融风险，本文以我国六大银行股指数据为研究对象，利用ARMA-GJR-SkT模型作为单一资产序列的边缘分布，以灵活的R-Vine Copula模型为基础，联合构建投资组合模型。通过滚动时间窗口的Monte Carlo技术及MST-PRIM算法确定各类模型的RVM结构，在此基础上结合逆变换法仿真模拟收益率序列，并利用模拟收益率进一步计算VaR与CVaR，最后经返回值检验法对模型进行验证。结果表明：建立最优的投资组合模型是精准度量金融风险的关键；在风险度量时，相同的置信水平下，CVaR模型比VaR模型更可靠。置信水平不等时，其值增大的同时，失败天数会减小。

动态R-Vine Copula模型； Monte Carlo模拟；CVaR;MST-PRIM算法

0 引言

随着金融市场一体化、全球化发展，银行股指数据间的波动通常具有跨地区的相依性，同时伴随着银行业系统性风险的出现，而精准度量这种风险的关键在于构建资产间的投资组合模型。众多学者[1-5]将目光投放到Copula函数的研究上，Copula被引入到金融领域中广泛应用的同时，其自身也得到了迅速的发展。自从Embrechts等[6]利用Copula函数分析金融数据以来，无论从维数上，还是动态时变性方面都得到了进一步扩展。比如Patton等[7]利用动态Copula模型分析了国际外汇市场的动态相关性；李平等[8]通过建立Copula模型，进一步模拟或有可转换债券(CoCo)定价，并在此模型的基础上数值分析；葛亮[9]采用Copula-GARCH模型对上证交易所新兴产业指数与上证综合指数构建五个二元Copula模型，并用GOD模型对数据尾部进行分析，事实证明：极端情形下两指数的涨跌幅度较大；吴鑫育等[10]通过构建随机Copula模型来研究中国股市量价间的尾部相关性，最终结果表明：中国股市量价尾部相关性展现明显的动态特征；鲁思瑶等[11]针对2015年股灾和2016年熔断期间的上证综、中证综合债以及上证基金间的相关性，通过利用扭曲混合Copula和RAMA-GARCH-T模型实证分析，研究表明：扭曲混合Copula模型较混合Copula模型能更好地拟合各资产日收益率间的相关结构；许可等[12]采用混合Copula函数刻画银行业间的复杂相关性，进一步度量商业银行面临的主要风险；韩超等[13]采用R-Vine Copula模型解决股份制商业银行系统性风险精准度量问题，并以历史重现原则仿真VaR，为金融风险管理研究者提供了风险度量的量化方法。银行业股指数据间的传染性往往会影响其投资组合风险度量的准确性，因此构建合理的银行股指数据间的投资组合模型，能够为进一步精准度量银行系统性风险提供可靠的理论支撑。

银行业系统性风险度量是近年来学者们[14-16]所青睐的热点之一，目前应用较多的是风险价值(VaR)、条件风险价值(CVaR)以及Mean-CVaR。例如，叶莉等[17]基于CoVaR方法对我国商业银行系统性风险溢出效应进行分析，研究结果表明：过去十年间，从宏观和微观两个层面比较分析了银行之间的溢出效应与风险传染方向；翁志超等[18]以商业银行指数和互联网金融指数收盘价数据为研究样本，建立了GARCG-Copula-CoVaR模型来度量互联网金融对商业银行的系统性风险溢出效应，得出了互联网金融对不同类型商业银行的系统性风险溢出具有异质性结论。上述文献均从静态的角度讨论了金融风险特性，但对序列数据的动态波动特点并未做过多研究，而金融序列数据的时变性已经是一个不可忽视的研究课题。

因此，本文从序列波动的动态方面出发，利用滚动时间窗口的Monte Carlo技术进行仿真模拟，最终得到每日的VaR以及CVaR预测值。在上述文献的基础上，从下面几个方面进行研究：首先，选取我国具有代表性的六大银行股指数据为研究对象，利用ARMA-GJR-SkT模型作为边缘分布，通过对单一资产序列进行拟合，充分解释了金融序列非对称性以及ARCH效应等方面的分布特征；其次，利用R-Vine Copula模型连接各边缘分布，由于R-Vine结构在选择pair-Copula函数时具有其独特的灵活性，因此经过最大生成树(MST-PRIM)算法得到最优的藤结构，使投资组合模型更加合理；另外，本文整个过程采用滚动时间窗口的Monte Carlo模拟技术完成，故在仿真模拟以及VaR和CVaR的计算上遵从动态的时变性原则；最后，通过理论成熟的Kupiec检验完成了模型验证，分别选95%和99%的置信水平，对比讨论了VaR与CVaR的在度量金融风险上的优点和不足。

1 模型的构建

1.1 边缘分布

由于股票收益率序列往往具有非对称性及“尖峰厚尾”等分布特征，因此本文选择具有偏学生分布的ARMA(p,q)-GJR(1,1)-SkT模型作为边缘分布进行刻画序列的这些特性。具体公式为

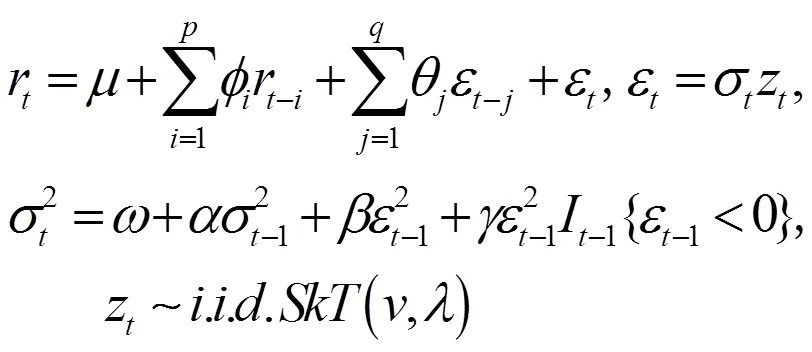
1.2 R-Vine Copula模型与参数估计

精准度量金融风险的关键在于构建合理的投资组合模型，在各类Vine Copula模型中，R-Vine Copula在选择pair-Copula函数时更灵活，刻画金融序列的复杂相依性时优越性更强，因此本文以R-Vine Copula来建立投资组合模型。考虑到该模型比较复杂，这里采用R-Vine矩阵法(RVM)[19~22]来表示其结构，一个维R-Vine Copula模型联合密度形式为

R-Vine Copula模型的参数估计采用极大似然估计法，具体步骤为：首先根据最大生成树MST-PRIM算法[23]来选择R-Vine结构，然后利用赤池信息准则(AIC)以及贝叶斯信息准则(BIC)确定Pair-Copula函数，最后通过极大似然估计法估计出所有的未知参数。AIC与BIC的具体计算公式为

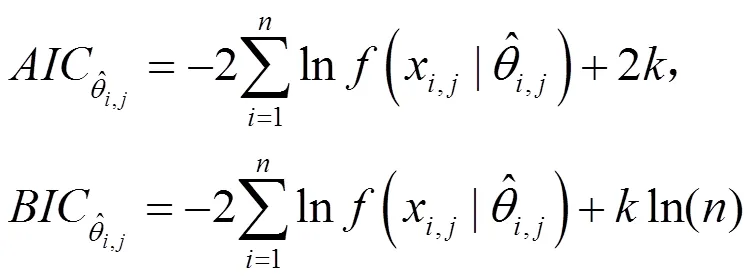
1.3 仿真模拟及模型预测

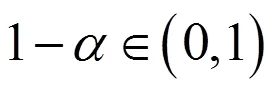
为了有效验证银行业金融市场波动的时变特点，采用具有动态性的滚动时间窗口Monte Carlo技术[20]进行仿真模拟并预测，具体做法如下：

(5)在样本量恒定为1386的情况下，将样本区间向后推一天，再进行(2)~(4)过程就可以得到第+1日(第1388日)的VaR与CVaR预测值；

(6)反复进行步骤(5)，可以计算出第1389，1390直到第1686日的VaR与CVaR值，即得到样本外300天的投资组合VaR与CVaR。

1.4 模型检验

2 实证分析

2.1 数据说明与处理

图1 六支股票指数收益率波动图

图1为六支股票收益率序列波动图，从图中可以很明显看出：前4支序列的波动幅度整体较小，而平安银行(PA)和招商银行(ZS)股指收益率序列波动幅度较大；除了金融序列固有的“典型特征”之外，不同的序列数据在相同的时间段波动趋势极其相似，说明序列之间还存在复杂的相依关系，因此选择GARCH族以及Vine Copula模型刻画它们之间的分布特征显得很有意义。

2.2 数据分析与参数估计

为了进一步量化分析收益率数据的分布情况，这里首先对其进行描述统计分析，结果如表1所示。由结果可得：各序列的偏度均大于0，峰度大于3，具有典型的“尖峰厚尾”、右偏特征，说明股票收盘价整体呈现上涨趋势，并且不适合用正态分布去拟合，J-B检验也充分证实了这一结论。另外由各阶滞后的LM检验结果显示：各序列检验统计量对应的值都小于0，拒绝原假设，即认为各序列存在明显的ARCH效应。综合以上分析：选取具有时变性、动态性及非对称性的ARMA-GJR-SkT模型作为序列的边缘分布颇为恰当。

由于本文采用能够体现动态与时变特性的滚动时间窗口Monte Carlo模拟法进行参数估计与仿真模拟，在滚动计算过程中共进行了300次建模，每次建模所选择的样本数据都不同。因此这里只给出了首次滚动的ARMA-GJR-SkT模型的参数估计及检验结果，具体如表2所示。

表1 原始数据的描述性统计分析结果

注：括号内为J-B统计量和L-M统计量对应的值

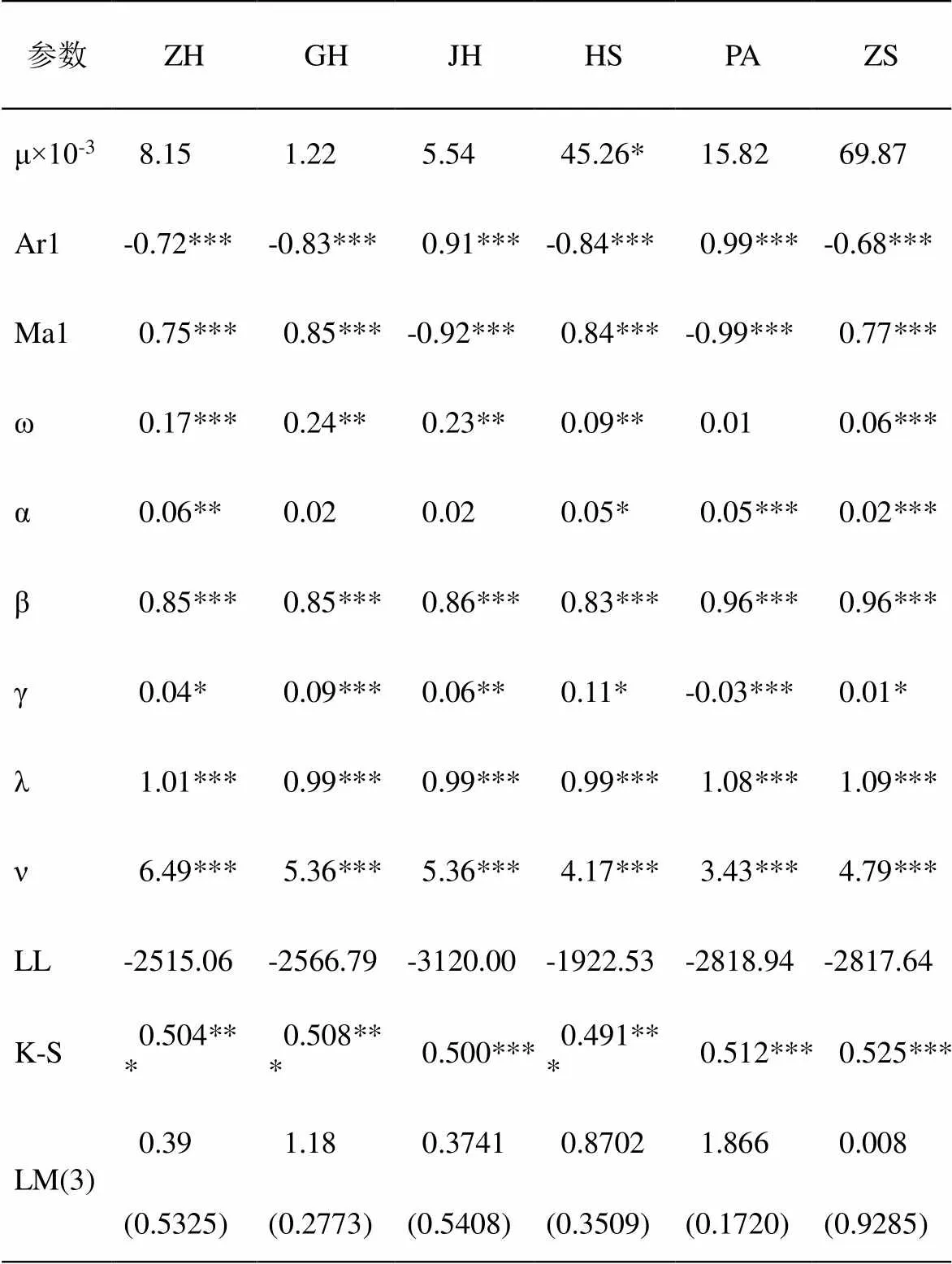
表2 各序列边缘分布模型ARMA(1,1)-GJR(1,1)-SkT参数估计结果

注：LL为模型估计的对数似然值，“***，**，*”表示在1%，5%，10%的水平下显著，LM(3)为ARCH效应检验，括号中的数字对应检验统计量的值

由表2结果可得：除均值之外，大部分参数在1%的显著性水平下均显著，模型整体也通过了检验。对原序列的K-S检验结果表明：原序列在5%的显著性水平下均显著，即认为概率积分化处理之后的残差序列服从0-1均匀分布。 LM(3)检验对应的值均大于给定的显著性水平5%，可以认为残差序列的波动不存在ARCH效应，从而进一步体现了ARMA-GJR-SkT模型作为边缘分布的合理性。

表3 R-Vine首次滚动的RVM结构的参数估计及检验结果

为了更直观看到R-Vine首次滚动的RVM结构，这里给出了RVM结构图，同样1、2、3、4、5、6分别表示ZH、GH、JH、HS、PA以及ZS，图2与表3中的树结构完全吻合。

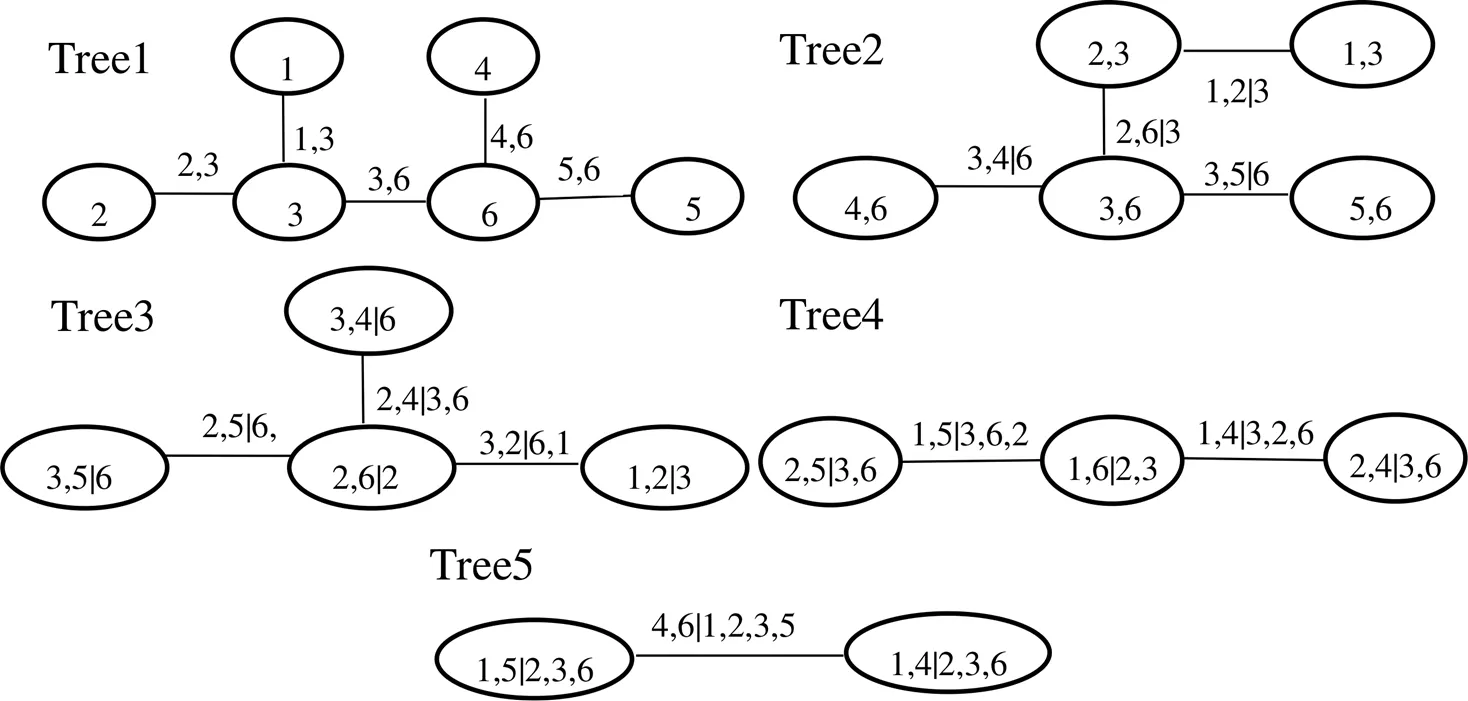
图2 R-Vine首次滚动的RVM结构图

2.3 风险度量与模型检验

建立合理的投资组合模型，其目的在于精准地度量金融风险。度量金融风险的方法有很多，本文选择风险价值(VaR)以及条件风险价值(CVaR)来实现模型的预测效果。计算投资组合VaR时，本文通过Monte Carlo模拟技术，结合逆变换法反推得到仿真模拟的日收益率数据，在给定置信水平为95%与99%时分别求得VaR值，然后通过与原始投资组合收益率相比，进而得出总失败天数，最后通过Kupiec检验得出相应的统计值与值，具体结果见表4。

表4 R-Vine Copula模型VaR预测效果及Kupiec检验结果

由于组合的VaR可能超过组合中各资产的加权平均VaR，因此，本文利用具有次可加性的CVaR来进一步度量组合的风险，具体如表5所示。

表5 R-vine Copula模型CVaR预测效果及Kupiec检验结果

由表4和表5可得：无论在95%还是在99%的置信水平下，VaR与CVaR的Kupiec检验结果对应的值均大于各自的显著性水平，因此没有理由拒绝原假设，即认为模型预测精准，拟合较合理；其次，从两个表中可以明显看出：随着置信水平的增大，风险价值减小，即失败天数随着置信水平的增大而减小；另外，在相同的置信水平下，CVaR预测结果整体高于VaR，而CVaR反映了一定置信水平下发生损失超过VaR的平均损失，因此在风险度量时显得更加可靠。图3更清楚地反映了两种置信水平下的CVaR预测结果。

图3 不同置信水平下的CVaR与原序列投资组合收益率对比图

3 结论

选取六大银行业股票收盘价数据作为研究样本，经计算得到的各序列收益率数据不仅表现出明显的金融数据的“典型特征”，还具有复杂的相依性和波动的动态时变性。本文以ARMA(1,1)- GJR(1,1)-SkT模型作为边缘分布，以灵活的R-Vine Copula模型为基础，联合建立了投资组合模型，通过滚动时间窗口的Monte Carlo模拟技术进行仿真模拟，从静态的低维研究上升到高维的动态研究，在理论和实际操作上都有了进一步突破。

在六大银行股指序列的风险度量方面，本文不仅采用动态VaR模型进行预测，还选用CVaR模型做进一步预测，通过两种预测结果对比得出：在相同的置信水平下，CVaR在风险度量时更加可靠，比VaR模型更具稳健性；置信水平不等时，随着置信水平的增大，风险价值减小，即失败天数减少。

[1] Chen P, Zeng W L, Chen M, et al. Modeling arterial travel time distribution by accounting for link correlatio-ns: a copula-based approach [J]. Journal of Intelligent Transportation Systems, 2019, 23(1): 879-890.

[2] Lyes K. Extreme Risk Modeling: An EVT-pair- Copulas Approach for Financial Stress Tests[J]. Journal of Banking and Finance, 2016 (70): 3-12.

[3] 谢赤,李洪琼.金砖国家股指期货市场的相关结构及谱风险度量——基于Vine-Copula模型的实证研究[J].金融理论与实践, 2019(6): 1-8.

[4] 韩超,周兵.高维动态藤Copula函数建模、仿真及在金融风险研究中的应用[J].数学的实践与认识, 2019, 49(12): 16-20.

[5] 韩超,严太华.基于高维动态藤Copula的汇率组合风险分析[J].中国管理科学, 2017, 25(2): 10-20.

[6] Embrechts P, McNeil A, Straumann D. Correlation: Pitfalls and alternatives [J]. RISK, 1999, 12(5): 69-70.

[7] Patton Andrew J.Modeling asymmetrics changes rate dependence [J]. International Economic Rview, 2006, 47(2): 527-554.

[8] 李平,尹菁华,来娜,等.基于Copula双变量模拟的CoCo债券定价[J].系统工程学报,2016,31(6): 772-782.

[9] 葛亮.基于Copula-GARCH模型的新兴产业与上证指数相依性研究[J].统计与决策,2016(24):170-173.

[10] 吴鑫育,李心丹.中国股市量价尾部相关性研究——基于随机copula模型的实证[J].金融理论与实践,2017(1):93-97.

[11] 鲁思瑶,徐美萍.基于扭曲混合Copula和ARMA- GARCH-t模型的投资组合风险分析——以上证综指、中证综合债和上证基金为例[J].数理统计与管理,2017,36(6):1131-1140.

[12] 许可,刘亚南,张峰.基于混合Copula的商业银行整合风险度量研究[J].商场现代化,2017(7):146-147.

[13] 韩超,周兵,熊亚.基于高维动态R-Vine Copula的股份制商业银行系统性金融风险计量研究[J].数学的实践与认识,2019,49(16):306-314.

[14] Matthew G N, Viet H N, Barry R. Risk and return spill-overs among the G10 currencies[J]. Journal of Financial Markets, 2016, 31: 43-62．

[15] 黄冬阳,宋光辉,董永琦.股票市场风险测度方法:文献综述[J].财会月刊,2019(3):147-158.

[16] 李荣,刘露.Mean-CVaR准则下延期支付供应链决策与协调[J].系统工程学报,2017,32(3):370-384.

[17] 叶莉,李园丰,王远哲.基于CoVaR方法的我国商业银行系统性风险溢出效应测度[J].河北工业大学学报,2019,48(5):81-90.

[18] 翁志超,颜美玲.互联网金融对商业银行的系统性风险溢出效应测度[J].统计与决策,2019,35(22): 159-163.

[19] 谢赤,李洪琼.金砖国家股指期货市场的相关结构及谱风险度量——基于Vine-Copula模型的实证研究[J].金融理论与实践,2019(6):1-8.

[20] 林宇,梁州,林子枭,等.基于高维R-vine Copula的金融市场投资组合优化研究[J].系统工程理论与实践,2019,39(12):3061-3072.

[21] 谢敏,胡昕彤,柯少佳,等.基于vine-Copula的发电商运营损益动态风险VaR评估方法[J].电力系统自动化,2019,43(5):39-45,52.

[22] 朱鹏飞,唐勇,张仁坤.国际主要股票市场联动性——基于藤Copula-HAR-RV模型[J].系统工程,2018, 36(9):16-29.

[23] Xiong F, Jun L I. Network Resource Risk Forecast Based on Vine Copula-GARCH Model[J]. Journal of Hubei University of Technology, 2016, 31(5): 68-71.

[24] Kupiec P. Techniques for verifying the accuracy of risk measurement models [J]. Journal of Derivatives, 1995,3(2): 173-184.

RESEARCH ON BANK STOCK INDEX PORTFOLIO AND RISK MEASUREMENT BASED ON DYNAMIC R-VINE COPULA

*XU Gang-gang, DI Qian-zi,SHI Hui

(College of Mathematics and Physics, Xinjiang Agricultural University, Urumuqi, xinjiang 830052,China)

The fluctuation of financial asset prices often has structural dependence. In order to study the complex relationship between banking stock index data and further accurately measure the financial risk, this paper takes the six major stock index data of China's banking as the research object, Using arma-gjr-skt as the marginal distribution of a single asset sequence, Based on the flexible r-vine copula model, jointly build the portfolio model. The RVM structure of various models is determined by the Monte Carlo technique of rolling time window and mst-prim algorithm. On this basis, the return sequence is simulated by inverse transformation method, and the VaR and CVaR are further calculated by the simulated return rate. Finally, the model is verified by back-testing method. The results show that the establishment of the optimal portfolio model is the key to accurately measure the financial risk. Given the same level of confidence in risk measurement, CVaR model is more reliable than VaR model.When the confidence level is different, the number of failure days will decrease as the value increases.

dynamic R-Vine Copula model; Monte Carlo simulation; CVaR; MST-PRIM algorithm

F830.59

A

10.3969/j.issn.1674-8085.2020.05.003

1674-8085(2020)05-0010-08

2020-05-06；

2020-06-17

新疆维吾尔自治区高校科研计划项目(XJEDU2018Y021);新疆农业大学大学生创新创业计划训练项目(dxscx2020518)

*徐刚刚(1989-)，男，甘肃平凉人，助教，硕士生，主要从事数理统计与金融统计研究(E-Mail:907252735@qq.com);

狄千姿(1999-)，女，新疆乌鲁木齐人，新疆农业大学数理学院2018级本科生(E-Mail:1602857468@qq.com);

石 慧(2000-)，女，重庆人，新疆农业大学数理学院2018级本科生(E-Mail:2190212874@qq.com).