一种新的L-fuzzy粗糙集的刻画方法

孙守斌 胡 凯

(1.聊城大学 计算机学院，山东 聊城 252059；2.聊城大学 数学科学学院，山东 聊城 252059)

0 引言

1982年，Z.Pawlak 提出了粗糙集理论[1,2]，用于研究和处理信息系统中的模糊和粒度以及进行数据分析.随后粗糙集理论得到了迅速的发展，取得了许多有益的成果.众所周知，粗糙集理论在数据的决策与分析、模式识别、机器学习与知识发现等方面都有很好的应用.研究粗糙集的方法多种多样，覆盖是一种基本的方法[3-8].许多学者用邻域的方法研究粗糙集也有许多好的结论[9-16],在模糊拓扑中，邻域和远域都起着非常重要的作用，利用远域理论在相当广泛的框架下建立了比较完整的Moore-Smith收敛理论，那么在粗糙集理论中用远域理论刻画近似算子就是很自然的事情了.笔者及其合作者利用远域理论刻画了上近似，并得到了许多好的结论.

1 预备知识

设L是带有逆和对应“′”的完全分配格，X是非空的集合，LX是L-fuzzy集合.LX中的最大元和最小元分别记为1X和0X.设a∈L，a叫做素元，若对L的任意元b,c，当a≥b∧c时,有a≥b或a≥c.设a∈L，a叫做余素元，若对L的任意元b,c，当a≤b∨c时,有a≤b或a≤c.L中非单位元的素元，记为P(L)，L中非零元的余素元，记为J(L),LX中非0X的余素元，记为J(LX).

2 L-fuzzy远域系统

在这一节，我们将定义广义的L-fuzzy远域系统以及上近似，并分别讨论串行的、自反的、弱传递的、弱一元的和传递的等性质.

定义3 一个映射FRN:J(LX)→2LX称为广义的L-fuzzy远域系统，如果对任意的xλ∈J(LX)和K∈FRN(xλ)，K≠0X.这里FRN(xλ)称为xλ的远域系，K∈FRN(xλ)称为xλ的远域.

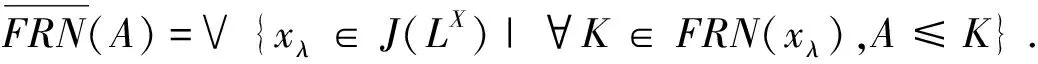
下面我们在广义的L-fuzzy远域系统下分别定义串行的、自反的、弱一元的、弱传递的和传递的，并讨论它们的性质.

定义5 设FRN是广义的L-fuzzy远域系统，则

(FRN1) 称FRN是串行的，如果任给xλ∈J(LX)和K∈FRN(xλ)，K≠1X；

(FRN2) 称FRN是自反的，如果任给xλ∈J(LX)和K∈FRN(xλ)，xλ∉K；

(FRN3) 称FRN是弱一元的，如果任给xλ∈J(LX)和K,V∈FRN(xλ)，存在M∈FRN(xλ)使得K∨V≤M；

(FRN4) 称FRN是弱传递的，如果任给xλ∈J(LX)和K∈FRN(xλ)，存在V∈FRN(xλ)使得对任意的yλ∉V存在Vyλ∈FRN(yλ)且K≤Vyλ；

(FRN5) 称FRN是传递的，任给xλ,yλ,zλ∈J(LX)和K∈FRN(yλ)，M∈FRN(zλ)，若xλ∉K且yλ∉M，则xλ∉M.

命题1 设FRN是广义的L-fuzzy远域系统，则

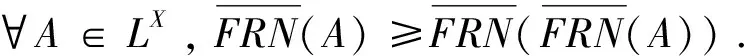
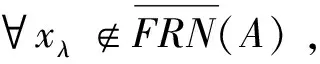
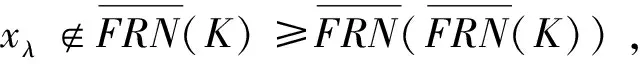
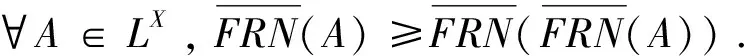
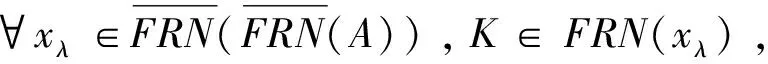
下面的例子表明这个命题反过来不成立.

例1 设X={x,y,z}，L={0,1}，这里模糊点的高度只能是1，即形如x1，为了方便我们直接写成x，最小元“0X”，实际上就是∅，于是我们得到

FRN(x)={∅,{y},{z}}，

FRN(y)={∅,{x,z},{z}}，FRN(z)={∅,{x},{y}}，则

3 近似算子的公理化刻画

证明必要性 由命题1易得结论成立.

充分性 设f:LX→LX是一算子满足(FT1)和(FT2)，定义FRNf如下

∀xλ∈J(LX)，A∈LX，A∈FRNf(xλ)当且仅当存在B∈LX，A≤B且xλ∉f(B).

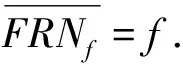
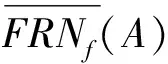
(FT1)：f(0X)=0X；(FT2)：若A≤B，则f(A)≤f(B)；(FT3)：f(1X)=1X.

充分性 设f:LX→LX是一算子满足(FT1)，(FT2)和(FT3)，FRNf的定义如定理1.显然，我们只需证明(FT3)蕴含串行的条件.事实上，∀xλ∈J(LX)，由f(1X)=1X得xλ∈f(1X)，这表明1X∉FRNf(xλ)，

所以FRN是串行的.

(FT1)：f(0X)=0X；(FT2)：若A≤B，则f(A)≤f(B)；(FT4)：∀A∈LX，A≤f(A).

充分性 设f:LX→LX是一算子满足(FT1)，(FT2)和(FT4)，FRNf的定义如定理1.显然，我们只需证明(FT4)蕴含自反的条件.事实上，∀xλ∈J(LX)，A∈FRNf(xλ)，由FRNf的定义得，存在B∈LX使得A≤B且xλ∉f(B).由(FT4)知B≤f(B)，于是xλ∉B，故xλ∉A，所以FRNf是自反的.

(FT1)：f(0X)=0X；(FT2)：若A≤B，则f(A)≤f(B)；(FT5)：∀A∈LX，f(A)≥f(f(A)).

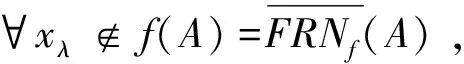
充分性 设f:LX→LX是一算子满足(FT1)，(FT2)和(FT6)，FRNf的定义如定理1.显然，我们只需证明(FT6)蕴含弱一元的条件.事实上，∀xλ∈J(LX)，K,V∈FRNf(xλ)，由xλ∉f(K)且xλ∉f(V)得xλ∉(f(K)∨f(V))=f(K∨V).因此存在M∈FRNf(xλ)使得K∨V≤M.所以FRNf是弱一元的.

4 结 语

笔者及其合作者基于广义的远域系统定义了上近似算子，并讨论了一些基本概念的性质，这些性质丰富了粗糙集理论.在分明集中，若a∈X且A∪A′=X，则a∉A当且仅当a∈A′.但对于模糊点与模糊集而言xλ∉A与xλ∈A′一般不等价.因此用远域系统刻画下近似算子遇到了困难，这正是我们下一步要考虑的问题.今后我们将用远域系统刻画粗糙集理论中的一些概念，进而讨论它们的性质.我们相信远域系统和邻域系统一样，在粗糙集理论中得到广泛的应用.