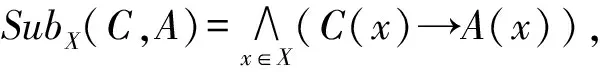模糊划分及其模糊粗糙近似算子
姚 卫 陈晓庆
(河北科技大学 理学院,河北 石家庄 050018)
0 引言与预备知识
粗糙集理论由Pawlak于1982年提出[1,2],是基于不可分辨关系的一种聚类方法.经过几十年的发展,粗糙集理论与方法已成功地应用到了过程控制、社会经济、医疗诊断、生物化学、环境科学、心理学和冲突分析等领域中.
最初的粗糙集的基本结构是等价关系,然而这并不能描述信息系统中的一些粒化问题,于是基于广义关系的粗糙集模型得到了快速发展.除关系型粗糙集外,覆盖型和邻域型(包括邻域系统和邻域算子)粗糙集也应运而生.邻域型粗糙集可以看做是覆盖型粗糙集的一种特殊情形,而覆盖型粗糙集可以看做是关系型粗糙集的扩展,二者都具有明显的粒化思想.
粗糙集和模糊集的交叉结合也是粗糙集理论的一个重要组成部分.在关系型模糊粗糙集模型方面,从模糊二元关系和赋值格的扩展两方面涌现了大量的研究论文,如:基于单位区间的模糊粗糙集[3-12],基于剩余格的模糊粗糙集[13-16]; 在覆盖型和邻域型模糊粗糙集模型方面,由于模糊覆盖诱导的不同类型的邻域系统及其上下近似算子,因此也就诱导了很多不同的粗糙近似算子模型[17-20].此外,文[21]提出了具有分析学背景的度量型粗糙集,研究了这种模型在模糊聚类中的应用.
由于等价关系和划分是两个相互等价的概念,因此二者在研究粗糙集时是等价的.对于模糊情形,通常的模糊等价关系是利用格值上的三角模对经典等价关系的逻辑扩展,其定义方式较为固定.是否存在与模糊等价关系一一对应的模糊划分的概念,一直是模糊数学界关注的问题.2004,Belohavek基于完备剩余格、利用模糊等同价系引入了一种模糊划分的概念[22],并证明了模糊等价关系和模糊划分之间一一对应性.在此之前的模糊粗糙集的相关结构都是建立在模糊覆盖的基础上的,模糊覆盖虽然是划分的一种弱化后的模糊扩展,但是无论如何它始终无法与模糊等价关系相对应.
本文将以含幺序半群(不必交换)为取值域,引入一种模糊划分的定义,推广Belohavek的相关定义,并证明它与模糊等价关系的一一对应性,最后以交换单位quantale为取值格研究模糊划分诱导的模糊粗糙近似算子的基本性质.
下面给出本文所需要的预备知识.
定义1 设L是一个偏序集,*是L上的一个半群运算,e是L中关于运算*的单位元.如果运算*与偏序相互协调,即a≤b,c≤d蕴含a*c≤b*d(∀a,b,c,d∈L),则称(L,*,e)是一个含幺序半群.
定义2[23]设(L,*,e)是一个交换的含幺序半群,其中L是完备格,如果运算*对任意并分配,即a*
例1 (1) ([0,+∞),×,1])和([0,+∞)op,+,1])都是交换的含幺序半群.
(2) ([0,1],×,1)和([0,1],min,1)是交换的单位quantale.
(3) 设L={0,a,b,1}是一个菱形格,即0 在本节中,我们假定(L,*,e)是一个交换的含幺序半群. 定义3 设X是一个非空集,映射R:X×X→L称为X上的一个模糊等价关系,如果 (R1) 自反性:∀x∈X,R(x,x)≥e; (R2) 对称性:∀x,y∈X,R(x,y)=R(y,x); (R3) 传递性:∀x,y,z∈X,R(x,y)*R(y,z)≤R(x,z). 定义4 非空集X的模糊子集族Φ⊆LX称为X上的一个模糊划分,如果 (P1) 对于任意的C∈Φ,存在x∈X使得C(x)≥e; (P2) 对于任意的x∈X,存在C∈Φ使得C(x)≥e; (P3) 对于任意的C1,C2∈Φ和x1,x2∈X,有C1(x1)*C2(x1)*C1(x2)≤C2(x2). 注1 设Φ是非空集X上的一个模糊划分,则 (P3′) 对于任意的C1,C2∈Φ和x1,x2∈X,C1(x1)*C2(x1)*C2(x2)≤C1(x2). 证明我们只需要交换C1和C2就完成了(P3)和(P3′)的相互转化. 我们称 (P3)和 (P3′)为“三换一”规则. 命题1 设Φ是非空集X上的一个模糊划分,则对任意的x∈X都存在唯一的Cx∈Φ使得Cx(x)≥e. 证明对任意的x∈X,设有C1,C2∈Φ使得C2(x)≥e和C1(x)≥e.对任意的y∈X,由三换一规则,C1(y)=e*e*C1(y)≤C1(x)*C1(x)*C2(y)≤C2(y).则C1≤C2.同理,C2≤C1.因此C1=C2. 在下文中,我们假设R是非空集X上的一个模糊等价关系.对于任意的x∈X,定义映射[x]R:X→L为[x]R(y)=R(x,y),称为x在R下的模糊等价类. 命题2 设R是非空集X上的一个模糊等价关系,则ΦR={[x]R|x∈X}是一个模糊划分. 证明显然,[x]R(x)=R(x,x)≥e,则(P1)和(P2)成立.由R的对称性和传递性,对于任意的a,b,x,y∈X有,[x]R(a)*[y]R(a)*[x]R(b)=R(x,a)*R(y,a)*R(x,b)≤R(y,b)=[y]R(b),从而(P3)成立.因此ΦR={[x]R|∀x∈X}是一个模糊划分. 命题3 设Φ是非空集X上的一个模糊划分,则对于任意的x,y∈X都有Cx(y)=Cy(x). 证明由三换一规则,Cx(y)=Cx(y)*e*e≤Cx(y)*Cy(y)*Cx(x)≤Cy(x).同理,Cx(y)≥Cy(x)因此,Cx(y)=Cy(x). 设Φ⊆LX是一个模糊划分,定义RΦ:X×X→L为RΦ(x,y)=Cx(y)(∀x,y∈X). 命题4 设Φ是非空集X上的一个模糊划分,则RΦ是一个模糊等价关系. 证明(R1) 由命题1易得.(R2) 由命题3易得. (R3) 对于任意的x,y,z∈X, RΦ(x,y)*RΦ(y,z)=Cy(x)*Cy(z)=Cy(x)*e*Cy(z)≤Cy(x)*Cx(a)*Cy(z)≤Cx(z)=RΦ(x,z). 因此,RΦ是一个模糊等价关系. 引理1 设ΦR是非空集X上的一个模糊划分,有Cx=[x]R,其中Cx为命题1中模糊划分对应的模糊子集. 证明对于任意x∈X,有[x]R(x)=R(x,x)≥e,由命题1中的唯一性可知,Cx=[x]R. 引理2 设ΦRΦ是非空集X上的一个模糊划分,有Cx=[x]RΦ其中Cx为命题1中模糊划分对应的模糊子集. 证明对于任意的y∈X,有[x]RΦ(y)=RΦ(x,y)=Cx(y).因此,[x]RΦ=Cx. 定理1 设R是非空集X上的一个模糊等价关系,Φ是非空集X上的一个模糊划分,则(1)RΦR=R;(2)ΦRΦ=Φ.因此,模糊等价关系和模糊划分之间存在一一对应性. (2) 首先,ΦRΦ={[x]RΦ|x∈X}.由引理2,对于任意的x∈X,[x]RΦ=Cx.则ΦRΦ⊆Φ.其次,对于任意的C∈Φ,存在x∈X使得C(x)≥e,我们有C=Cx=[x]RΦ.从而ΦRΦ⊇Φ.因此,ΦRΦ=Φ. 称为由模糊划分Φ诱导的上、下粗糙近似算子.有意思地是,这两个粗糙近似算子还有如下描述方式. 定理2 设Φ是非空集X上的一个模糊划分,则对于任意的A∈LX和x∈X,有 (O4) 首先,对于任意的C1,C2∈Φ和y∈X,由三换一规则有 注2 公式(O1,O3)解释为:x∈aprΦ(A)当且仅当[x]⊆A,当且仅当对于任意的C∈Φ,x∈C蕴含C⊆A,当且仅当存在C∈Φ使得x∈C且C⊆A(注意C其实就是[x]).1 模糊划分与模糊等价关系的一一对应性

2 模糊划分诱导的模糊粗糙近似算子