具有多选评判集的高校实验室绩效模糊综合评价

郭慧媚 郑彩芬 杨晓斌 林亨斌 杨晓鹏

(1.韩山师范学院 数学与统计学院，广东 潮州 521041；2.韩山师范学院 资产管理处，广东 潮州 521041)

关键字 模糊综合评价;多选评判集;实验室绩效;区间值

0 引言

实验室绩效评价，是指综合考虑实验室的多个评价指标，兼顾定性评价和定量评价，科学、规范、客观的绩效评估方法.对实验室的绩效评价，是高校实验室管理和建设的重要环节，也是提高高校实验室建设质量的有效措施之一[1-3].一般实验室主要功能为开展实验研究和探索，而高校实验室还兼具教学功能.绩效考评的关键是绩效指标的选取和评价方法的确定.绩效指标一般根据不同学校的条件和要求、不同类型实验室的功能、不同学科和专业的特点等进行选取.目前，高校实验室绩效评价指标的选取，评价体系的确立，主要采用层次分析法[4-10].层次分析法的优点在于可以构建多个层次的指标体系，各个不同的指标具有不同的权重因子，从而体现每个指标对总体绩效的不同影响或重要程度.权重因子可以由特定的专家根据历史经验直接给出，也可以通过抽样调查，利用统计的手段获取.在获得各个指标的评价分值以及对应的权重因子之后，如何计算表示综合评价结果的数值，这是评价方法的核心.主要的评价方法包括模糊综合评价法[11-15]、基于决策树模型的方法[16,17]、基于集对理论的评价方法[18]等.

在经典的模糊综合评价方法中[11,19,20]，评审专家只能根据评判指标作出单一的选择.然而，评价本身就具有主观性.因此可能出现部分专家在作出评判选择时，难以确定被评判事物应该归属于哪个指标，而是在某两个指标之间犹豫.这种情况我们称之为具有多选评判集的情况.经典的模糊综合评价不再适合具有多选评判集的情况.为此，本文提出了基于区间值运算法则的模糊综合评价方法.

1 模糊综合评价方法简介

模糊综合评价方法是对受多个因素影响的事物或现象作出全面综合评价的一种有效的多因素决策方法.首先它全面考虑了影响事物的多种因素，其次它将人们对事物主观的甚至带有不确定性的评价进行量化，最后综合多个因素的量化评价，通过精确的推导计算，得到体现综合评价的结果.本节我们简单介绍经典的模糊综合评价方法.

设U={u1,u2,…,un}表示含有n种影响因素(或指标)的因素集，V={v1,v2,…,vm}表示含有m种评判的评判集.由于各种因素对事物的影响不同，地位和作用不同，因此一般情况下，各个因素也具有不同的权重.假设第j个影响因素uj的权重为aj∈[0,1],j∈J={1,2,…,n}，则影响因素的权重向量为

a=(a1,a2,…,an)∈[0,1]n.

(1)

它是一个n维模糊向量.人们对m种评判指标的评价结果经常也不是绝对的肯定或者否定，因此一般可以用一个介于0到1的模糊数来表示.假设对一个事物进行评价，第j个影响因素uj关于第i个评判指标vi的评价结果为模糊数rij∈[0,1]，j∈J,i∈I={1,2,…,m}，则评价结果可以用一个模糊矩阵表示

R=(rij)n×m,

(2)

矩阵R称为评判矩阵.

在得到评判矩阵之后，可以利用影响因素权重向量，计算综合评判向量b=(b1,b2,…,bm)，其中bi表示所评价的事物关于第i个评判指标的量化评价结果，i∈I.由评判矩阵R和权重向量a得到综合评判向量b，一般由下面式子进行计算

b=a∘R，

(3)

其中∘表示模糊合成算子.一般∘可取“取大-取小”(∧∨)、“取大-乘积”(∨，·)或“加法-乘积”(+，·)等合成算子[24].综合评判向量的计算结果b∈[0,1]m是一个模糊向量.

在得到计算综合评判向量b之后，如何确定综合评价的结果呢？这里我们列举两种比较常用的方法.

第一种方法，以向量b的最大分量所对应的评判指标作为对该事物的评价结果.比如，假设向量b的最大分量为bi*，即bi*=max{b1,b2,…,bm}，其中i*∈I，则对该事物的评价为vi*.

第二种方法，根据每个评判指标对评价结果的贡献程度，确定每个评价指标的分值.假设第i个评判指标对应的分值为vi，则我们得到评判指标的分值向量V=(v1,v2，…,vm)T.从而我们可以计算得到评价该事物的综合量化分值为

(4)

如果对多个事物进行模糊综合评价，就可以利用以上每个事物的综合量化分值，对多个事物进行排序，得到相应的评价结果.一般情况下，综合量化分值越高的事物，评价结果越好.

2 具有多选评判集的实验室绩效评价

在经典的模糊综合评价方法中，专家对事物的评价一般只能选取单个评判指标.例如，假设评判集为V={v1=优，v2=良，v3=中，v4=差}，则评审专家只能选择这四个指标中的一个，即只能“单选”.然而在某些情况下，评审专家可能难以确定所评价的事物应该属于哪一个评价指标，而是在某两个(甚至多个)评审指标之间犹豫.比如在上述情况下，个别专家可能会认为该事物可以是“优”，也可以是“良”.在这种情况下就会出现“多选”评判集，经典的基于单选评判集的模糊综合评价方法就失去了它的效果.因此，为了处理这类评价问题，本文提出了具有多选评判集的模糊综合评价方法，并将其应用于实验室的绩效评价.

2.1 基于单选评判集的评判矩阵计算方法

这一小节我们以实验室绩效评价模型为例，说明基于单选评判集的评判矩阵计算方法(见文献[24]).(1) 因素集U={u1,u2,u3,u4,u5}，其中：u1表示教学成果，u2表示科研成果，u3表示设备保养与维护，u4表示管理制度建设，u5表示设备利用与共享.(2) 评判集V={v1,v2,v3,v4}，其中v1表示“优”，v2表示“良”，v3表示“中”，v4表示“差”.(3) 建立评判矩阵.专家评审组的每个成员对被评判的对象(实验室)进行评价.假定评审组由c个专家组成，每个专家以投票的方式，选择评判集中的某一个评判指标，表明各自对对被评判对象的评价.例如对某一个实验室的教学成果(u1因素)，评审组中有c11个专家通过投票方式认为是“优”的，c12个专家认为是“良”的，c13个专家认为是“中”的，c14个专家认为是“差”的.对于其他因素，也通过投票方式得到相应的评价结果，则评价的结果可以利用表1加以描述.

表1 评审专家的投票结果

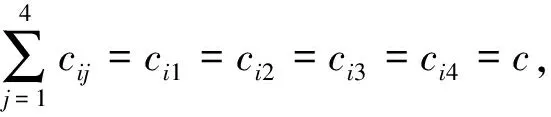
2.2 具有多选评判集的专家投票结果表示

前面我们已经介绍了经典的具有单选评判集的模型及其相应的模糊综合评价方法.为了评价具有多选评判集的模型，这一小节我们先介绍其模型特征以及评审专家投票结果的表示方式.

在具有多选评判集的模型中，评审专家在投票的时候，可以选择两个及以上的评判指标.例如，在上述实验室绩效综合评价模型中，对于实验室的其中一个因素的评价，如果专家确定其评价结果为“优”，则选择唯一的指标v1(优)进行投票；如果专家锁定了其评价结果为“优”或“良”，但又不能确定到底是“优”还是“良”，此时专家就可以同时选择这两个，即v1(优)和v2(良)进行投票.对于选择唯一指标的投票结果，我们称之为确定的投票结果，而对于选择两个及以上个指标的投票结果，我们称之为犹豫的投票结果.为了区分这两种类型的投票结果，我们以区间值的形式表示专家的投票结果.

例如对某一个实验室的教学成果(u1因素)，评审组中有c11个专家以唯一指标的投票方式认为是“优”，有c11个专家的投票含有两个及以上个指标，且包含了指标“优”.这样，对于因素u1，得到的单选的“优”的票数是c11，而得到的多选的“优”的票数是c11.显然，单选表示专家百分之百的肯定，而多选则意味着专家暂不确定，抱着犹豫的态度选了“优”.因此单选的“优”的权重明显应该大于多选的“优”的权重.我们不妨设单选的“优”的权重为1，而多选的“优”的权重为0.5，则该因素评价结果为“优”的票数可以表示为为[c11,c11+0.5c11].这样，左端点c11就表示确定的票数，而右端点c11+0.5c11则包含了确定和犹豫的等效总票数.

因此，具有多选评判集的专家投票结果表示利用表2进行描述.

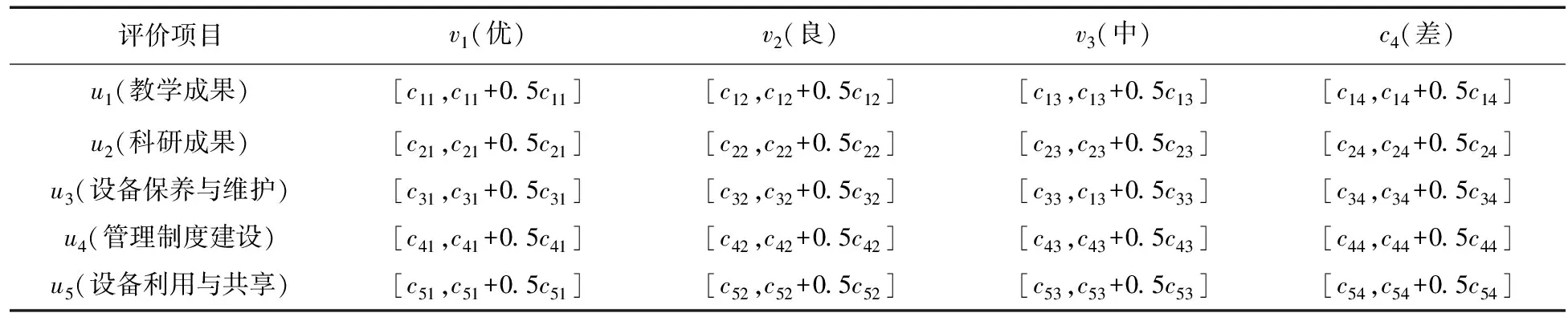
表2 具有多选评判集的评审专家投票结果

假如评审组的专家人数依然记为c，则表2中的投票结果显然满足ci1+ci2+ci3+ci4≤c≤ci1+ci1+ci2+ci2ci3+ci3+ci4+ci4，其中i∈{1,2,3,4,5}.

3 基于区间值运算法则的模糊综合评价方法

3.1 区间值运算法则

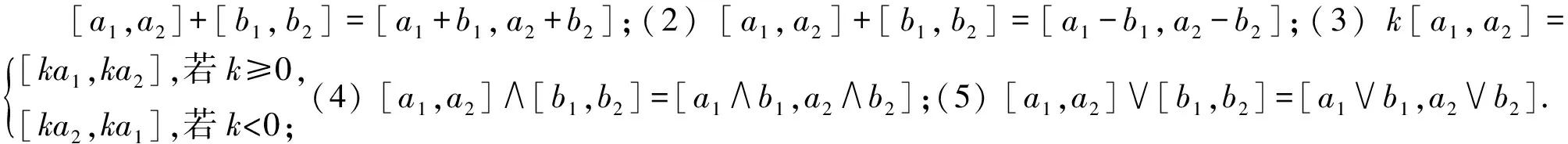
记全体区间值构成的数集为IV.为了比较两个区间值的大小关系，我们定义数集IV上的关系≤如下.

根据定义1容易验证下面的定理.

定理1 设[a1,a2],[b1,b2],[c1,c2]∈IV，则(1) [a1,a2]≤[a1,a2]；(2) 若[a1,a2]≤[b1,b2]且[b1,b2]≤[a1,a2]，则[a1,a2]≤[b1,b2]；(3) 若[a1,a2]≤[b1,b2]且[a1,a2]≤[c1,c2]，则[a1,a2]≤[c1,c2]；(4) 在[a1,a2]≤[b1,b2]和[b1,b2]≤[a1,a2]这两个式子中，必有一个式子成立.

根据定理1，“≤”是数集IV上的一个全序关系.定理1中的(4)表明，在序关系“≤”之下，任意两个区间值是可以比较大小的.

3.2 具有多选评判集的模糊综合评价方法

假设在具有多选评判集的实验室绩效综合评价模型中，评审专家的投票结果如表2所示，影响因素的权重向量为a=(a1,a2,a3,a4,a5).我们用矩阵

C=(Cij)=([cij,cij+0.5cij])

(5)

表示表2中的投票结果，并利用取大-乘积(·,∨)合成运算计算加权评价向量B=(B1,B2,B3,B4)；

(6)

其中⊙表示(·,∨)合成算子，

(7)

j=1,2,3,4.根据区间值的运算法则，向量B是可以计算出来的.在加权评判结果B=(B1,B2,B3,B4),B1表示对实验室绩效评价结果为“优”的加权票数，B2,B3,B4表示的意思类似B1.

为了更好地利用加权评价向量进行评价，我们进一步将评判集数量化.根据经验，评判集V={v1(优)，v2(良)，v3(中)，v4(差)}可以量化为V=(v1,v2,v3,v4)T=(1,0.75,0.5,0.25)T,接着在结合加权向量计算综合评价的总分

(8)

综合评价的总分越高，说明相应的实验室的绩效评价结果越好.

以上关于具有多选评判集的投票结果表示方式和综合评价方法，我们给出相应的模糊综合评价的步骤.

步骤1 确定因素集U={u1,u2,…,un}，其中uj表示影响被评判对象的影响因素，j=1,2,…,n，并确定影响因素的权重向量a=(a1,a2,…,an).

步骤2 确定评判集V={v1,v2,…,vm}，其中表示具体的若干个评价指标，i=1,2,3,…,m，并确定评判集的量化向量V=(v1,v2,…,vm)T.

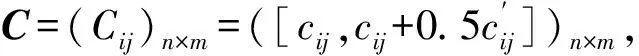
步骤4 根据影响因素权重向量a和表示评审专家投票结果的矩阵C，利用式子

(9)

计算加权评价向量B，其中⊙表示(·,∨)合成算子

(10)

步骤5 根据加权评价向量B和评判指标数量化之后的向量V，利用式子

(11)

计算综合评价总分S.

步骤6 根据综合评价总分，对被评判的对象进行模糊综合评价.总分越高，综合评价的结果越好.

4 数值例子

这节我们以实验室的绩效综合评价为例，说明本文提出的具有多选评判集的模糊综合评价方法的应用.

例基于模糊综合评价方法的实验室绩效评价模型.

步骤1 确定因素U={u1=教学成果，u2=科研成果，u3=设备保养与维护，u4=管理制度建设，u5=设备利用与共享}.并且，影响因素的权重向量为a=(a1,a2,…,a5)=(0.4,0.2,0.1,0.1,0.2).

步骤2 确定评判集V={v1=优，v2=良，v3=中，v4=差}，并且，评判集的量化向量为V=(v1,v2,v3,v5)T=(1,0.75,0.5,0.25)T.

步骤3 根据各个影响因素及相应的评判指标，专家评审组对被评判对象的进行投票评价.假设评审组共有10个专家成员.对每一个因素进行评价时，允许评审专家选择两个及以上个指标进行投票评价.针对三个不同实验室的投票结果分别表示为下列表4、5、6 的形式.

表3 专家评审组对实验室甲的因素u1的投票结果

对其他影响因素以相同的方式进行投票，可以得到对实验室甲的绩效评价的结果如下表4所示.

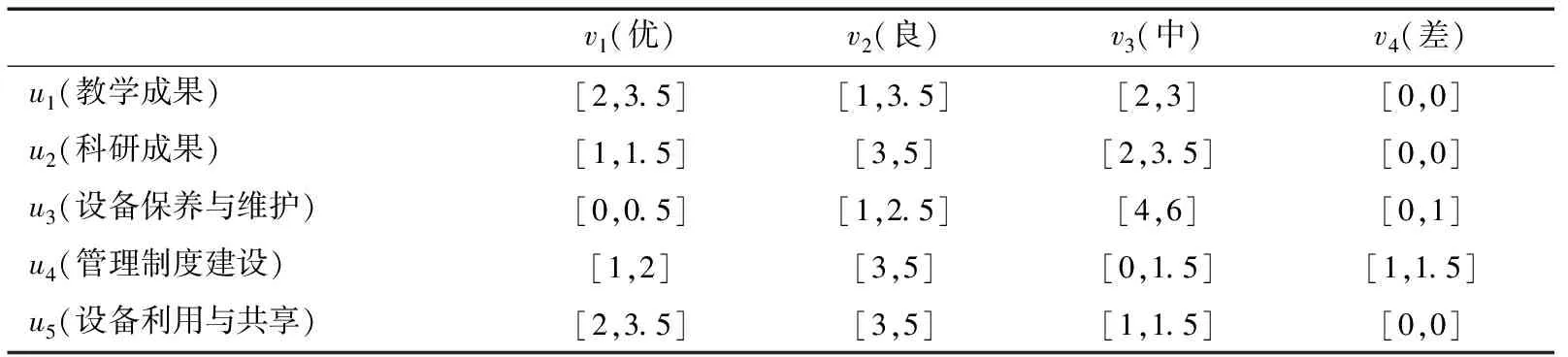
表4 实验室甲的评审专家投票结果

类似地，可以得到下面的表5和6.

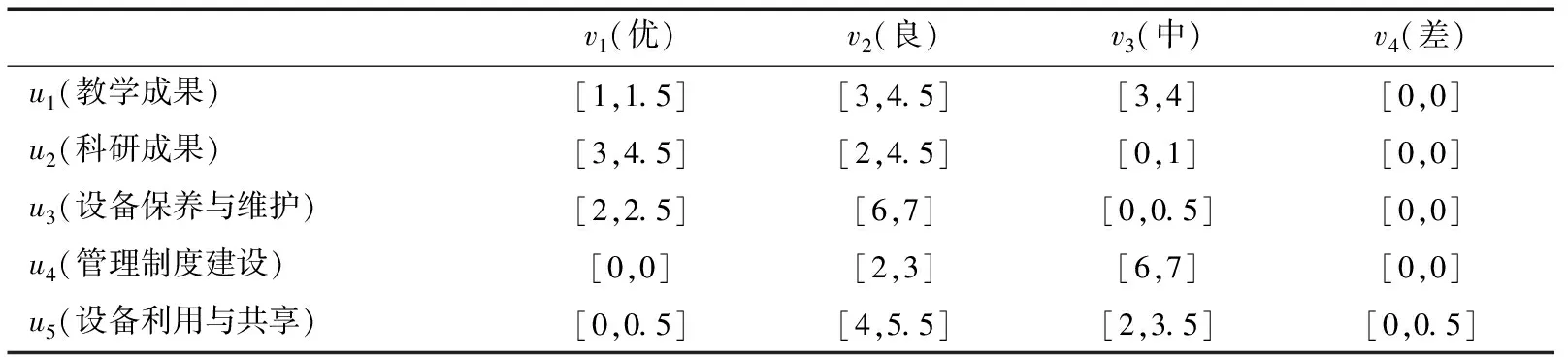
表5 实验室乙的评审专家投票结果

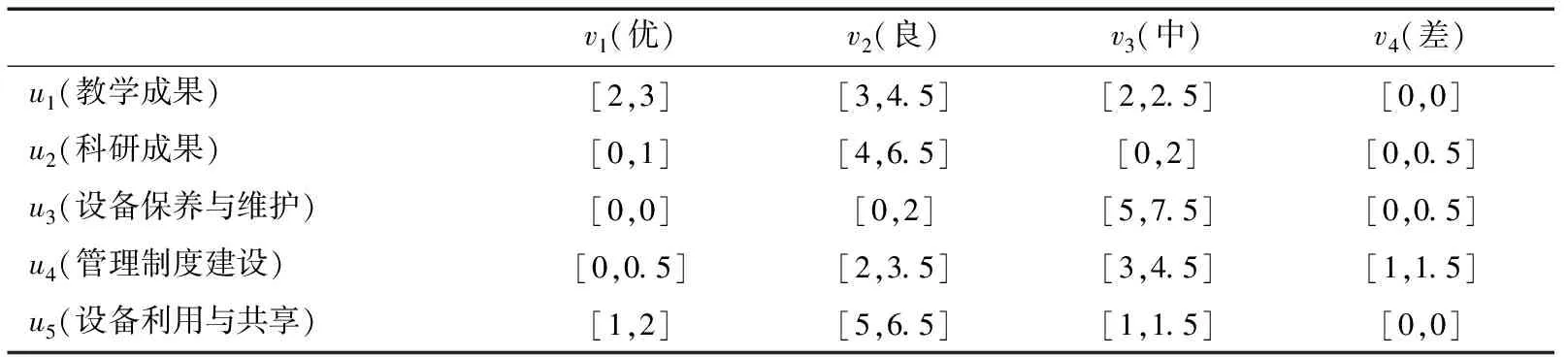
表6 实验室丙的评审专家投票结果

得到体现投票结果的矩阵分别为

(12)

步骤4 根据影响因素权重向量和表示评审专家投票结果的矩阵，利用式子(9)和(10)分别计算对实验室甲、乙、丙的加权评价向量B1、B2、B3.

=([0.8,1.4],[0.4,1.4],[0.8,1.2],[0.1,0.15]).

(13)

同理可以计算得到

B2=a⊙C2=([0.6,0.9],[1.2,1.8],[1.2,1.6],[0,0.1]),

B3=a⊙C3=([0.8,1.2],[1.2,1.8],[0.8,1.0],[0.1,0.15]).

(14)

步骤5 根据加权评价向量B和评判指标数量化之后的向量V，利用式子(11)计算对实验室甲、乙、丙的综合总分S1、S2、S3.

S1=B1·V=([0.8,1.4],[0.4,1.4],[0.8,1.2],[0.1,0.15])·(1,0.75,0.5,0.25)T=[1.525,3.0875],
S2=B2·V=([0.6,09],[1.2,1.8],[1.2,1.6],[0,0.1])·(1,0.75,0.5,0.25)T=[2.1,3.075],
S3=B3·V=([0.8,1.2],[1.2,1.8],[0.8,1.0],[0.1,0.15])·(1,0.75,0.5,0.25)T=[2.125,3.0875].

步骤6 根据综合评价总分，对被评判的对象进行模糊综合评价.根据步骤5的计算结果，实验室甲、乙、丙的综合评价总分分别为S1=[1.525,3.0875],S2=[2.1,3.075],S3=[2.125,3.0875].根据定义1的序关系，不难验证得到S1≥S2≥S3.

5 结论

高校实验室的绩效评价是实验室建设和管理的重要环节.经典的模糊综合评价方法只适用于具有单选评判集的模型.为了对具有多选评判集的情形进行评价，本文提出了基于区间值运算法则的模糊综合评价方法.具有多选评判集的专家投票结果可以利用区间值模糊数进行刻画，然后再利用相应的运算法则，求出每个被评判对象的综合评价总分并进行排序或者评价.本文提出的基于区间值运算法则的模糊综合评价方法也适用于其他具有多选评判集的综合评价模型.