圆形截面非均匀对称配筋的无量纲诺模图*

任志文 周东华 双超 李露 罗莎

(昆明理工大学建筑工程学院 昆明 650504)

0 引言

圆形截面是在工程中常见的截面形式，如桥墩、抗滑桩和桩基础等。《混凝土结构设计规范》[1](下文简称为《规范》)给出了计算圆形截面配筋的超越方程组，其求解的难点在于须迭代求解，通常超越方程组可能存在有很多解，迭代计算所得到的解是否是真正所需要的解，在很大程度上取决于给定的迭代初始值，因此迭代求解并不简单，还需有个经验积累的过程。在工程设计中求解超越方程组是十分不便的，也并不可取，而最为需要的是能简单快速计算的方法或能手算的工具。《规范》中引用了等效矩形应力图换算，而换算系数又是用矩形截面换算系数α1和β1，这样就存在了两次近似，换算时使得合力点的位置比真实位置外移了2.9%，导致内力壁增大，偏于不安全[2]。另外，《规范》公式是基于纵向钢筋沿圆周均匀布置推导的，一部分位于中性轴附近的钢筋因应变很小，其应力远小于屈服强度，使得这部分钢筋对截面承载力的贡献很小，这对于配筋量较大的大直径圆形截面(如抗滑桩)是很不经济的。因此本文拟通过推导、计算和绘制诺模图来提供方便设计人员手算的实用工具，同时还要考虑钢筋沿周边可不均匀布置的方式，即将计算上所需的受力钢筋尽可能地布置在远离中性轴的地方，从而增大力臂和提高钢筋的使用效率。

1 非均匀配筋计算方法推导

1.1 支撑条件

文中公式推导时所采用的符号含义均与《规范》中相应符号一致。混凝土与钢筋的应力应变关系(本构关系)采用《规范》给出的公式：

(1)

(2)

圆形和环形截面配筋及承载力计算的无量纲诺模图[2]中根据规范推出了混凝土和钢筋应变的变化范围，即图1的5个应变区域。

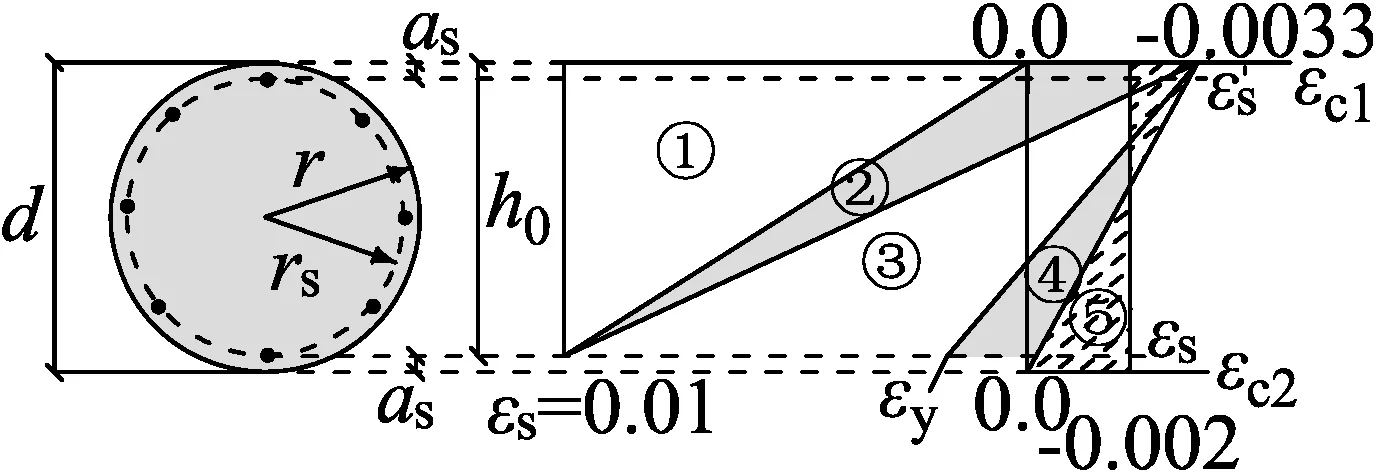
注：εc1、εc2分别为混凝土截面的上、下边缘应变；分别为钢混截面的上、下部钢筋应变。图1 混凝土及钢筋应变变化区域

如图1所示的5个应变区域，涵盖了混凝土与钢筋所有受力下可能出现的应变之间的变化情况。5个区域的特点以及对应的受力情况参考新的混凝土配筋计算方法:无量纲图表法[3]。

1.2 圆形截面中钢筋应力和内力计算

与常规规范[4-13]的设计理念不同的是，本文的配筋方式如图2所示，圆形截面中的上边缘与下边缘同样的角度内配均匀的受力钢筋。为方便积分计算，可先假定上面有受力钢筋的部分为90°，沿y轴对称分布，下面与上面部分沿x轴对称分布。

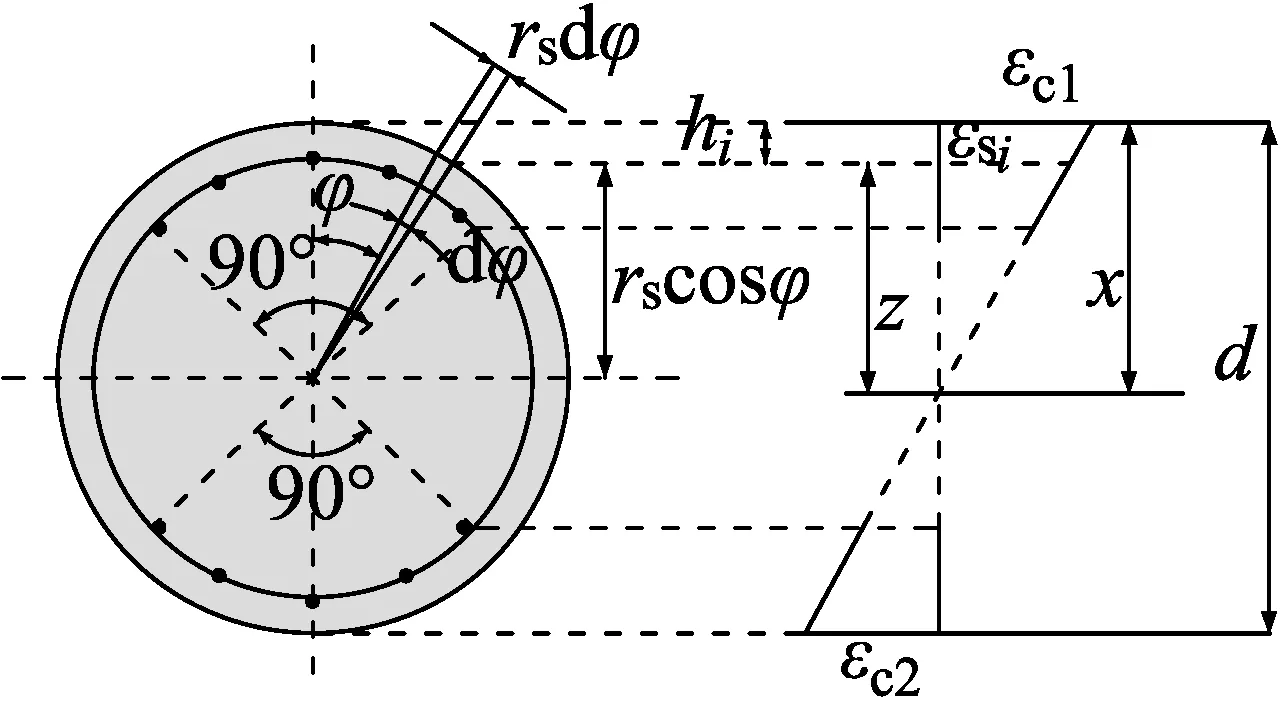
注：φ为截面任意角度；dφ为截面任意角度的积分增量；εsi为任意角度对应的应变；rsdφ为积分增量对应弧长；z为长度坐标。图2 钢筋截面参数

可以将均匀分布的钢筋等效看作连续的，钢筋的总面积(As)便会均匀地平摊到上下有受力筋的部分，由此部分的角度可得弧长为半圆的周长，因此钢筋总面积均摊到弧长为

(3)

根据混凝土和钢筋的应变对应变化，可以得出受压区高度与混凝土及钢筋应变之间的几何关系：

(4)

截面配筋部分任意单元处的应变(仅在有配筋部分使用，无配筋区域钢筋应变εs0=0)：

(5)

为了使式(5)中的z与截面配筋部分任意单元具有相关性，如图2所示引入参数hi，可得：

z=x-hi=x-(r-rscosφ)

(6)

(7)

将式(7)代入式(2)求得截面任意单元应力即

(8)

由图2可知，钢筋的应变随截面上边缘和钢筋下边缘的应变而改变，参考式(2)，钢筋应力的分布有两种形式，一种为三角形(-εy<εs<εy)，另一种为矩形(εs<-εy,εs>εy) 。两种分布形式的内力计算如下。

(1)矩形区钢筋应力弯矩计算

此区域与上面的区别是钢筋应力变为了一个常量，故此轴力及弯矩的计算如下

(9)

(2)三角形区钢筋应力弯矩计算

三角区截面钢筋任意单元的应变即为式(8)，对式(8)积分即可求得其轴力为

(10)

对过圆心的水平轴取矩积分可得到钢筋三角区的弯矩为

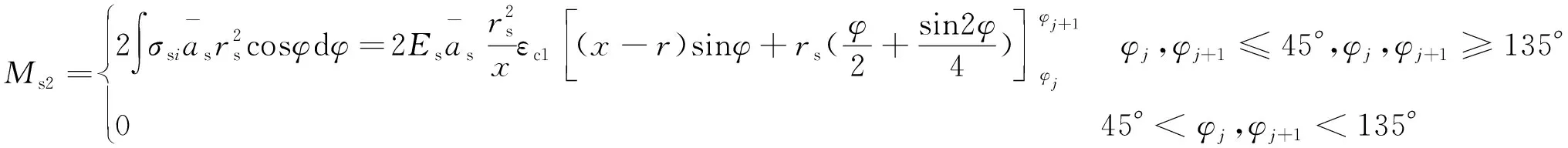
(11)

此时求得的轴力与弯矩与截面尺寸有联系，为了消除这种关联性，应将式(9)和式(10)除以πr2fc，式(11)除以πr3fc，即得到钢筋无量纲的轴力和弯矩。

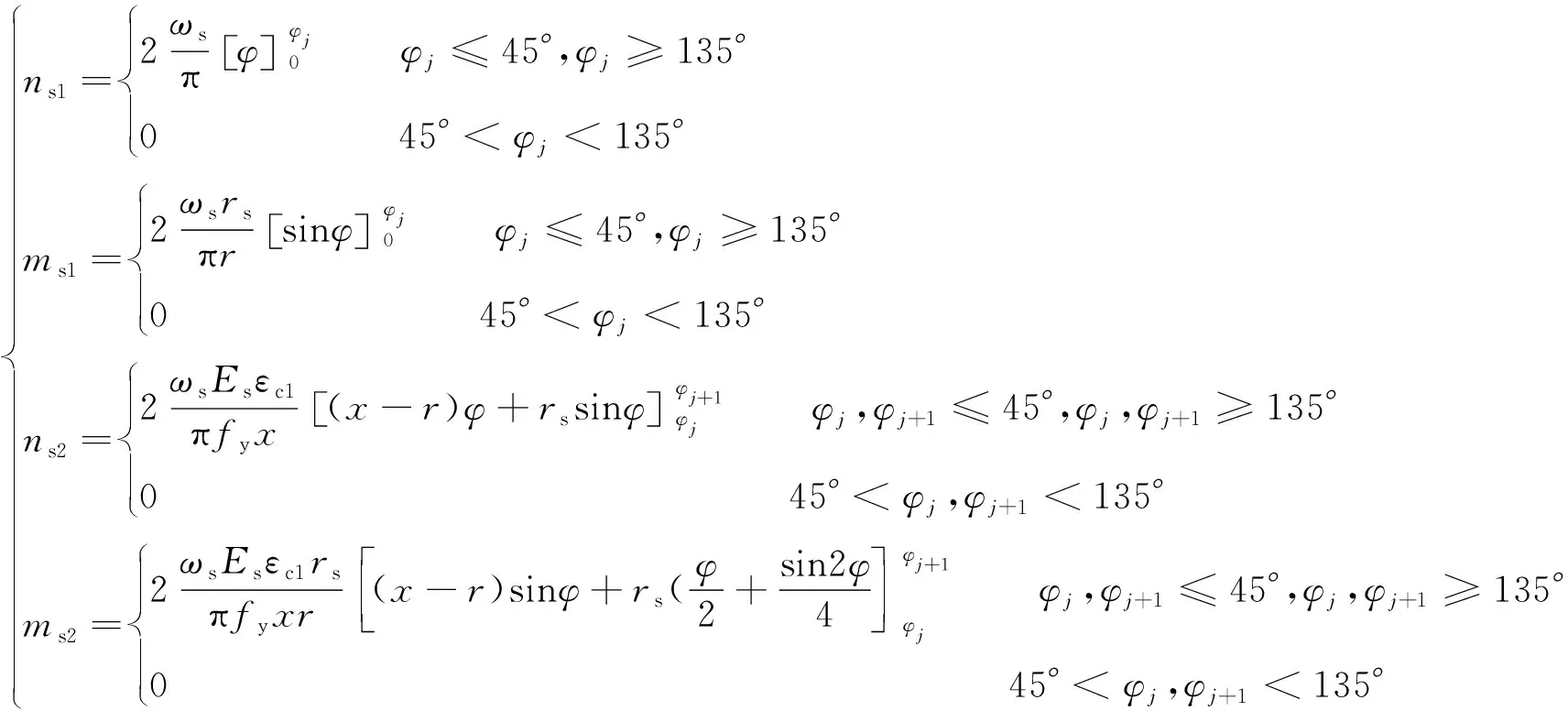
(12)

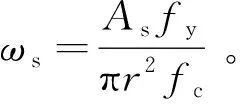
式(12)中的上下限与式(1)相关，εsi达到屈服应变前为弹性，属于三角形区，达到屈服应变后为塑性，属于矩形区。为方便表达积分上下限与应变区间的联系，引入一个值q，令q=(r-hi)/r，则圆心角φj=arccos(q)。结合图1的5种应变区域，可将式(12)中的上下限分为3种情况，如表1所示。

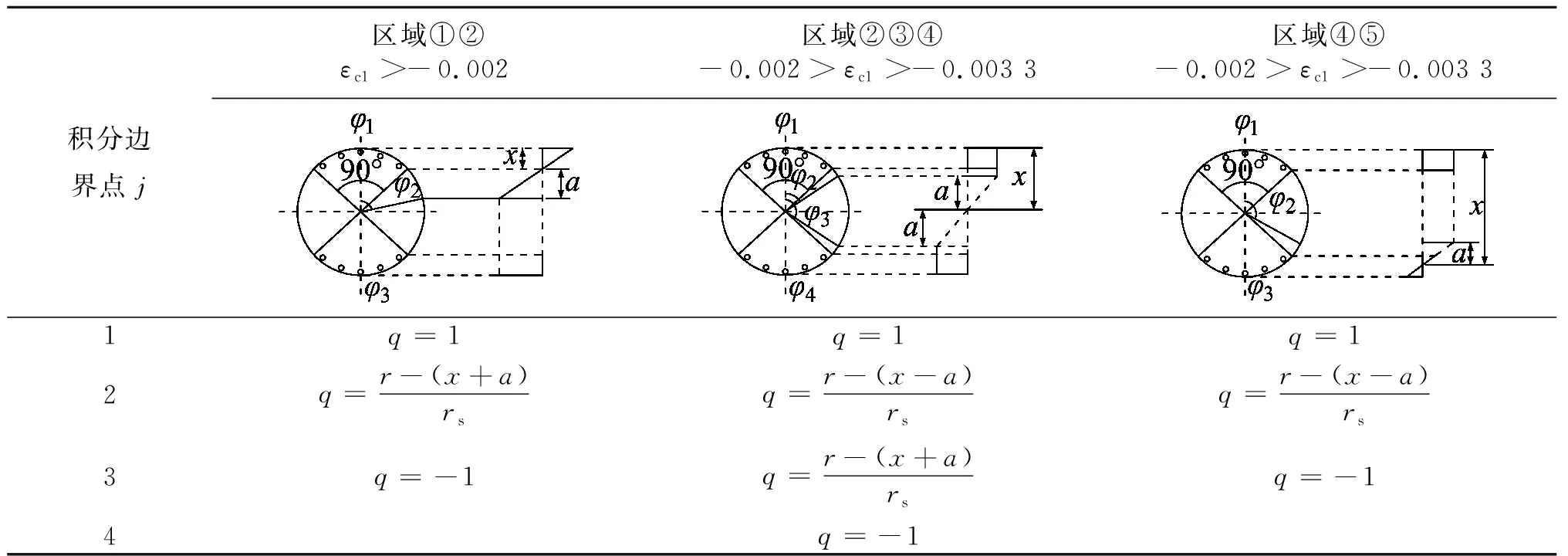
表1 钢筋各应变区积分角度计算

1.3 圆形截面中混凝土的应力和内力计算

与式(7)相同的原理可推出混凝土任意单元的应变与圆心角之间的关系如图3所示。

(13)

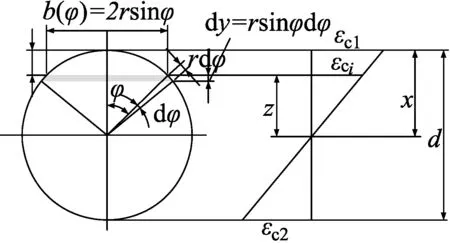
图3 混凝土截面参数

将式(13)代入式(1)便可得到圆形截面混凝土任意单元的应力。

(14)

引入系数K1、K2、K3，将式(14)改写为

(15)

与钢筋应变的三角形区和矩形区相似，混凝土的应变根据式(1)可分为抛物线区和矩形区。下面分别推导抛物线区和矩形区的内力及弯矩。

矩形区混凝土的轴力和弯矩为

(16)

(17)

抛物线区混凝土的轴力和弯矩计算由式(15)积分可得出此区域的轴力和弯矩为

(18)

(19)

同式(12)相似，为了消除轴力和弯矩与混凝土截面尺寸的联系，令式(16)和式(18)除以 πr2fc，式(17)和式(19)除以πr3fc，即是无量纲的轴力与弯矩。

(20)

式(20)的积分上下限可归纳为表2。

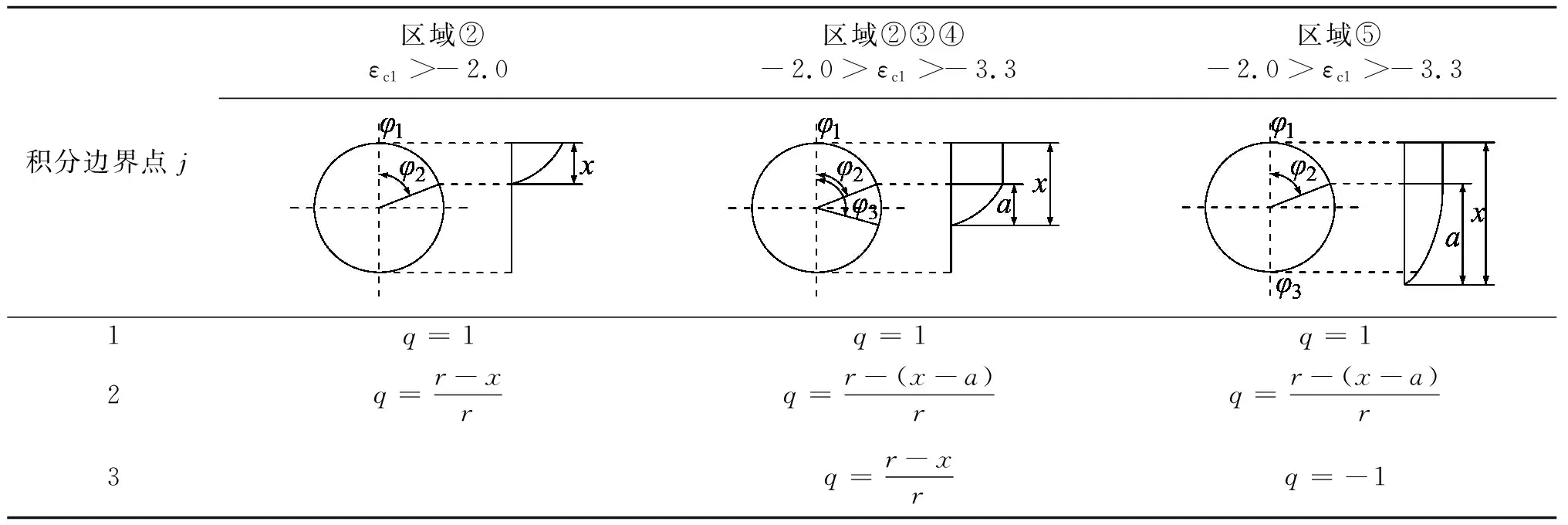
表2 混凝土各应变区积分角度计算

由钢筋和混凝土的无量纲弯矩，可根据应变的变化区间推导出总的无量纲轴力与弯矩，当满足εc1≥-0.002和εs≥-εy时，为

(21)

当满足εc1<-0.002和εs<-εy时，为

(22)

将构件破坏前的所有应变区域代入运算，混凝土应变与钢筋应变便成为了已知量，无量纲轴力也成为了已知量，对无量纲弯矩m赋值，即可得到相应的强度配筋率。使用Matlab软件编程计算即可得到图4，使此公式运用更为简便。

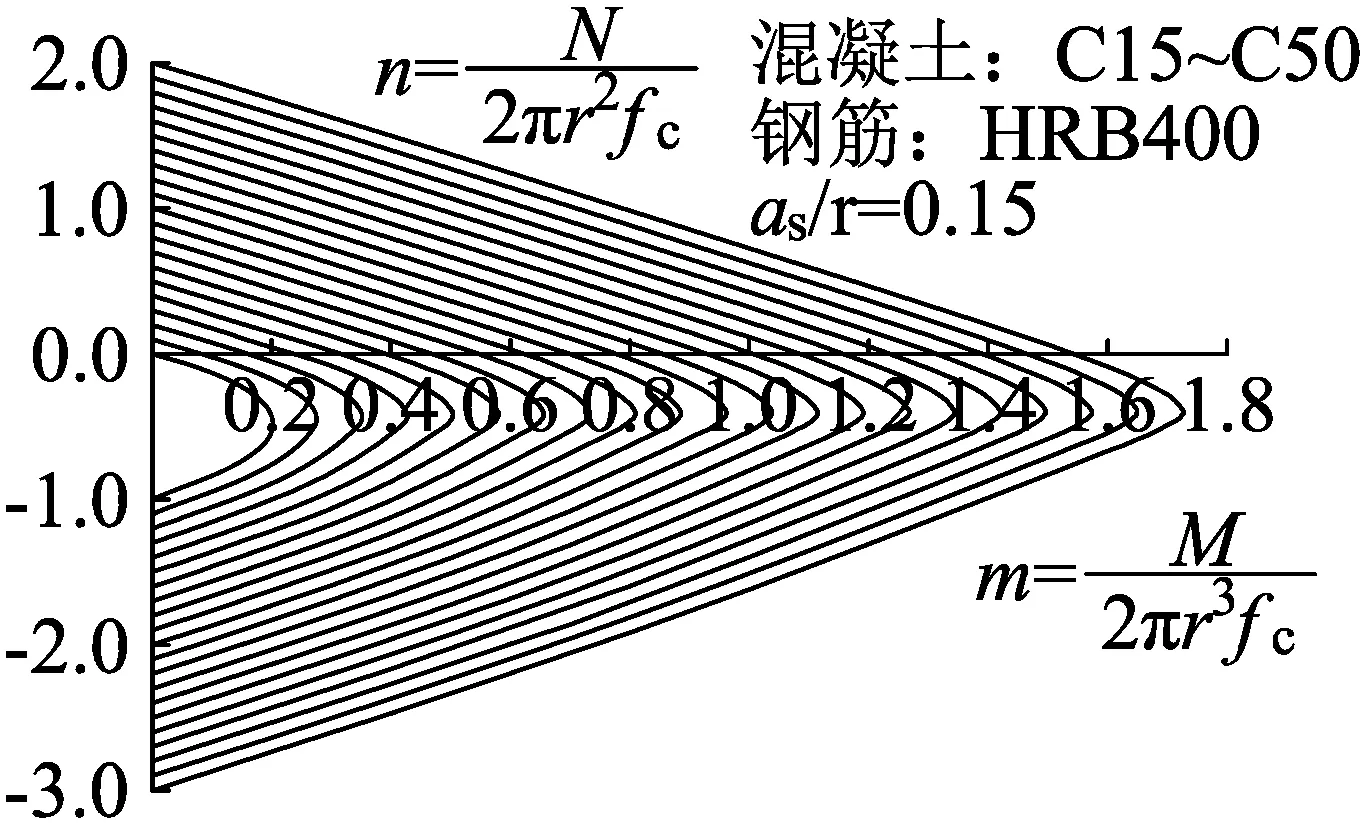
图4 圆形截面非均匀对称配筋诺模图

2 计算例题

为了验证本文的计算方法是否合理有效，特选取以下示例与规范配筋进行比较。已知圆形截面参数为：r=400 mm、as=60 mm、C40、HRB400。分别取不同的受力情况，且分别用《规范》与本文方法计算，结果如表3。

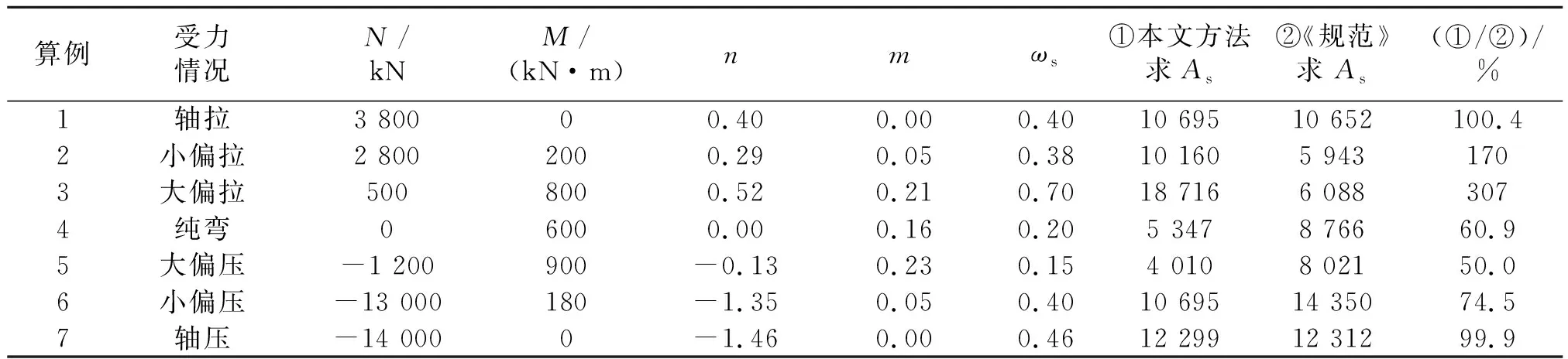
表3 算例1～7

由表3内的计算结果可以得到：《规范》仅可用于偏心受压，遇到小偏拉以及大偏拉时，算出的配筋面积比本文少了甚多，而本文的计算图皆由本构关系推导，《规范》的计算存在着两次近似的过程——等效矩形应力换算和换算系数近似值。因此本文的配筋方法相对更为合理。在轴压和轴拉时，配筋面积很接近，相对而言，本文的方法更加精确。而纯弯以及大小偏压都能不同程度地节俭钢筋，这是因为偏心受压以及纯弯时，中性轴附近钢筋应力小，非均匀配筋布置正是减少了中性轴附近的钢筋。

3 结语

与《规范》不同之处在于，本研究未使用矩形等效系数，全程利用积分的形式推导公式，消除了迭代所产生的误差的影响，使得配筋结果更加精确。《规范》属于超越方程，运算时还需计算机编程辅助才可求解，由截面钢筋混凝土应变间的关系得出：纯弯、大偏压和小偏压时，中性轴处钢筋应变小，钢筋未能达到合理利用，由算例可知，运算结果确实可有效地节省配筋面积，为工程实际提供一种简便且有效的圆形截面非均匀配筋计算方法。