高温后杉木枋碳化速度及力学性能研究*

王展光 王婷婷 邵建华

(1.凯里学院建筑工程学院 贵州凯里 556011； 2.江苏科技大学土木工程与建筑学院 江苏镇江 212003)

0 引言

黔东南地区是少数民族聚集区，其传统民居为穿斗式木结构，其采用木枋将木柱连接成整体，木枋的尺寸比汉式木结构的木梁尺寸小很多，一般截面尺寸在5 cm×15 cm左右。火灾是黔东南州穿斗式民居面临的最主要的灾害形式，木枋作为穿斗式木结构的主要受力构件，其抗火性能直接关系到穿斗式木结构的整体性能，对其火灾后的性能研究是木结构火灾后性能评价的重要依据。

在北美和澳大利亚等地民居大部分为木结构房屋，相关学者对木结构的防火也进行了大量的研究。LIE T T[1]综合考虑安全系数、材性劣化和荷载水平的影响，给出了受火木梁和木柱耐火极限的简化计算公式；BUCHANAN A等[2]将木材高温后的截面划分为炭化层、高温分解层和正常区域3个部分，认为内部剩余区域为不考虑温度影响的正常区域；FIRMANTI A等[3]通过试验发现受火木梁的碳化速度近似为常量，耐火时间受荷载影响，荷载越大降耐火时间越低；在相关学者的研究基础上，在欧美等国家的木结构设计规范中对不同木材碳化速度和耐火极限计算进行了相应的规定[4-7]。

在国内，对木结构防火性能进行了许多探索。刘静、张盛东等[8-9]提出了木结构抗火性能的主要热学参数，推导出木材温度场的理论公式；李帅希[10]对花旗松木梁、木柱受火后碳化速度和力学性能进行了试验和模拟；许清风、张晋等[11-13]对不同受火情况下木梁性能进行了研究，分析了剩余承载力、碳化速度的影响因素；陈玲珠等[14-15]通过对比国外相关规范的取值，提出了适合我国木结构耐火极限计算的方法；马京华[16]对小叶杨、花旗松和落叶松3种木材的剩余承载力性能进行了研究；王正昌[17]通过试验研究和有限元模拟研究了采用传统“一麻五灰”地仗工艺处理后对木梁、木柱耐火极限和受火后力学性能。由于现在国内木结构相对较少，国家建筑材料相关标准中对木结构的耐火性能的要求主要采用定性规定[18]；在《建筑设计防火规范》和《木结构设计标准》中也仅对各类木构件的耐火极限时间做出了相应的要求[19-20]。

由于木枋截面远小于木梁，在标准升温曲线下，木枋已经烧毁，因此本文在前期对旧松木枋耐火性能的基础上[21]，采用了5种最高温度的升温曲线，研究黔东南本地杉木枋在不同升温曲线后性能，分析不同加温温度下的碳化速度和剩余承载力。

1 试验研究

1.1 木枋试件

黔东南木结构大部分采用本地生长的杉木，因此本次试验的杉木枋采用本地杉木制作。通过对杉木进行相关测试，常温下杉木密度为359.3 kg/m3,含水率10.4%。杉木枋为矩形截面，采用木枋在实际工程中的尺寸，其中宽为42 mm，高为135 mm，长为800 mm，根据试验需要一共制作了12个试件。

1.2 加温试验

木枋试件加热使用的是课题组定制某公司生产的加热电炉，其采用电阻丝加热，感应器控制温度，电热炉最高温度1 000 ℃，能满足本试验需求。

在对松木枋耐火性进行研究时，其在600 ℃时松木枋受火断裂[21]，由于杉木的硬度和密度都要小于松木枋，其对高温耐火性能也要低于松木枋，所以本次试验最高温度设为500 ℃，采用最高温度分别为500、450、400、350、300 ℃的5种加温过程曲线见图1所示，并将5种加温情况下的性能与常温情况进行比较。将加工好的杉木枋试件放入加热电炉中，按照规定的升温曲线进行加热，加温结束后取出试件并进行浇水冷却。

图1 升温曲线

1.3 加载试验

加温后杉木枋进行三点弯曲试验和松木枋弯曲试验相同[21]，相关数据由试验机自带的IMP数据采集系统进行采集。

2 结果与讨论

2.1 高温后碳化情况

随着加温温度的升高，杉木枋表面的碳化程度越来越高；当温度大于350 ℃，木枋表面出现纵横向裂缝，且随着温度升高，裂缝宽度越来越大；当温度达到500 ℃时，杉木枋发生断裂，具体见图2。杉木枋在不同加温温度下的截面情况见图3。

图2 杉木枋高温后的形态

图3 杉木枋高温后截面情况

加温温度为300 ℃时，木枋表面几乎没有变化，木枋截面保存完整，表面有局部轻微碳化，但不是很明显，这是由于木材是在温度达到200～300 ℃开始分解，300 ℃以上才会形成碳化区，在最高温度为300 ℃的情况下，难以形成明显的碳化层。

加温温度达到350 ℃时为杉木枋表面完全碳化阶段，该阶段表现为矩形棱角碳化和外表面出现纵向裂纹，但碳化层还没有出现鳄鱼皮式裂缝，木枋整体还是比较完整。

加热温度达到400 ℃以上为木枋的碳化层加深阶段；这个阶段木枋剩余截面从内向外划分为3层，分别为正常区域、高温分解区和碳化区[21]。随着温度的升高，碳化区不断增大，正常区域不断缩小，木枋截面出现不同程度的弯曲变形，随着表面纵横向裂缝的发展，鳄鱼皮式裂缝越来越明显，局部发生破损断裂。

加温温度达到500 ℃为杉木枋断裂阶段，见图2，该阶段杉木枋发生断裂，只有端部有部分残留，将其截开(见图3)发现还保留少量木材材质。

2.2 碳化速度计算

选取木枋的1/3跨度作为木枋参考截面，根据该截面进行碳化速度计算，高温后的截面见图3，对杉木枋的碳化区、高温分解区和正常区域进行测量，通过相关公式，计算出杉木枋的碳化速度。

杉木枋碳化速度分别用Vb和Vh进行表示，其中Vb表示木枋宽度方向上碳化速度，Vh表示木枋高度方向上碳化速度，其公式为[14]

Vb=(B-b)/2t

(1)

Vh=(H-h)/2t

(2)

式中，B、H分别杉木枋截面常温情况下宽度和高度；b、h分别为木枋高温后宽度和高度；t为杉木枋在高温下的受火时间。

不同加温温度后杉木枋截面剩余的宽度和高度见表1，将相关结果代入式(1)和式(2)，可以得到杉木枋不同加温温度下的碳化速度，具体见表1，其中500 ℃时取截面全部碳化情况来进行计算。

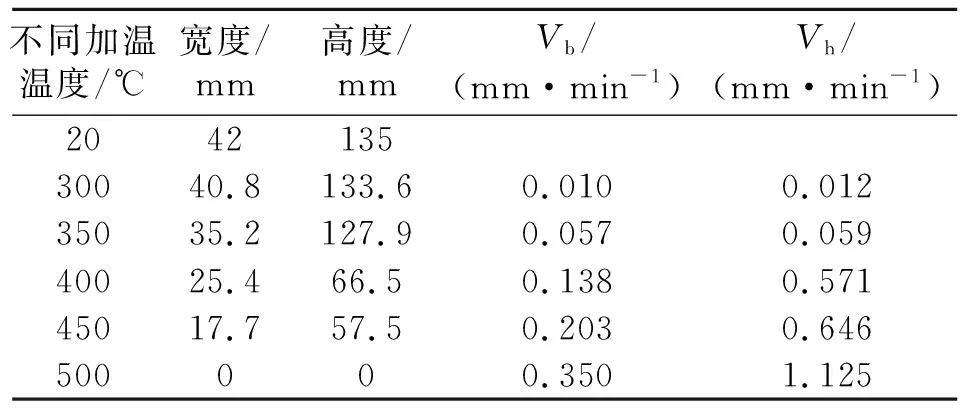
表1 杉木枋碳化速度

杉木枋碳化速度与温度关系见图4，杉木属于软木，根据欧美规范给出在标准升温曲线下软木炭化速度值为0.65 mm/min[4-7]。从表1和图4可以看出，杉木枋高度方向和宽度方向的碳化速度随着温度升高而增大；其宽度方向的碳化速度与加温温度近似为线性，碳化速度远小于欧美规范的推荐值；其高度方向的碳化速度要大于宽度方向的碳化速度，随着加温温度升高，高度方向的碳化速度增加值明显大于宽度方向增加值，当温度达到500 ℃时，其高度方向的碳化速度Vh达到1.125 mm/min，远远高于欧美规范的推荐值0.65 mm/min。

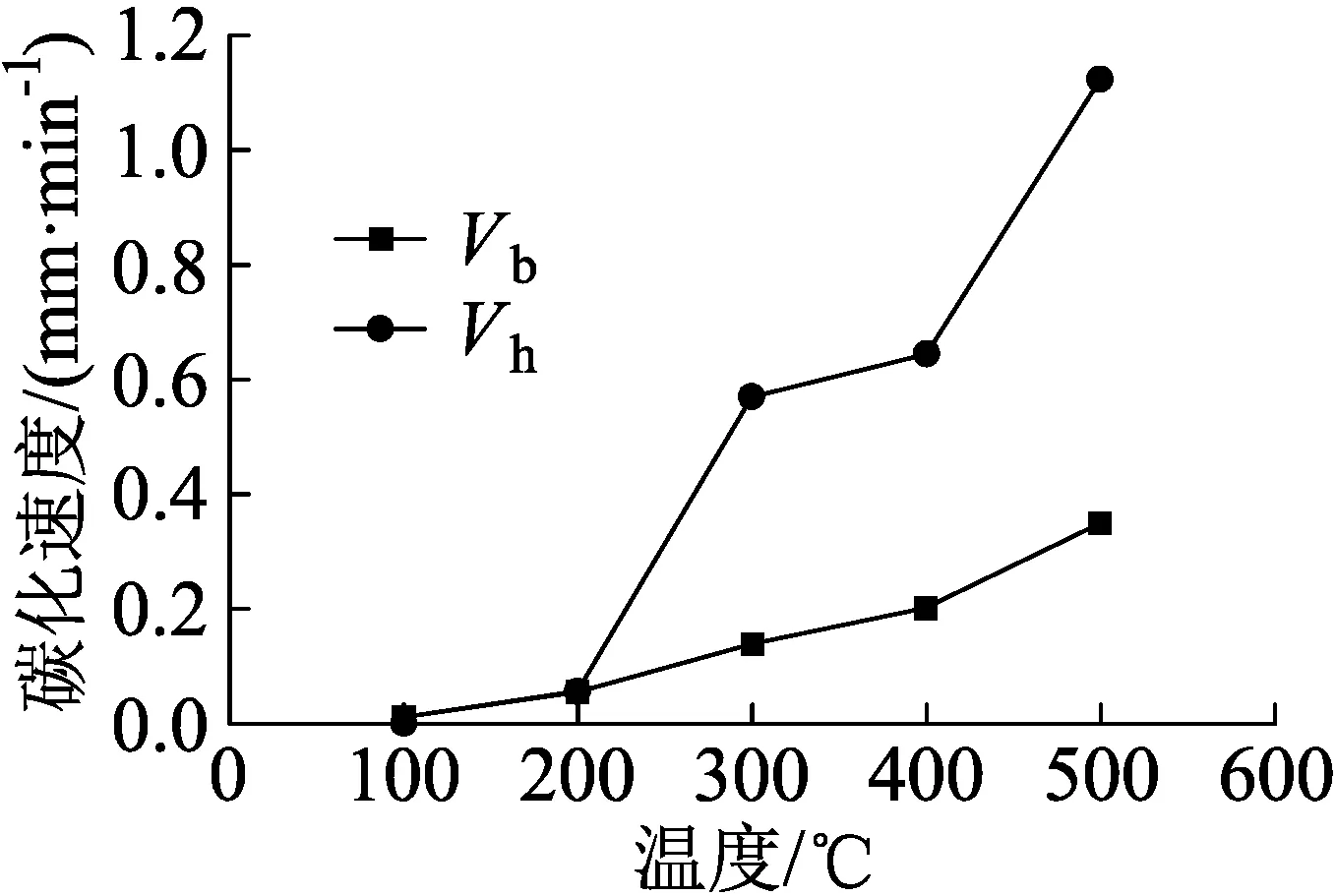
图4 杉木枋碳化速度与温度关系

2.3 加载试验和弯曲曲线

杉木枋的三点弯曲试验示意图见图5，木枋在试验过程中分为发出响声、出现明显裂纹和碳化层脱落、木枋破坏3个阶段。在第一阶段，木枋所受荷载较小，杉木枋在加载过程中不断发出轻微响声，表明木枋局部出现损坏；随着荷载增大，木枋的整体变形不断增大，木枋的裂纹不断扩展，在常温情况表现为木枋下侧出现几条细小的纵向裂纹，而加温后的木枋表现为下侧外表面碳化层裂缝宽度不断增加，并伴随着加载过程中出现碳化层不断脱落现象；当加载荷载达到极限荷载时，杉木枋承载能力会急速下降，在荷载位移曲线上表现为出现明显下降，这时常温情况的木枋下部几条细小裂纹相互贯通，形成较大纵向裂缝，杉木枋发生拉断破坏，见图6。

图5 木枋三点弯曲试验示意

图6 常温木枋破坏

三点弯曲情况下，杉木枋在不同温度下的荷载位移曲线可划分为弹性上升阶段和破坏下降阶段。弹性上升阶段，木枋的荷载随位移增大而增大；荷载达到最大值后，木枋承载力迅速下降，在荷载位移曲线上出现明显的下降段，此时木枋出现局部破坏而失去承载能力，见图7。从图中可以看出，高温后杉木枋剩余极限强度和抗弯刚度随着加温温度的升高而不断降低，当加温温度达到400 ℃时，杉木枋剩余强度下降非常明显，只有常温情况下的1/10。

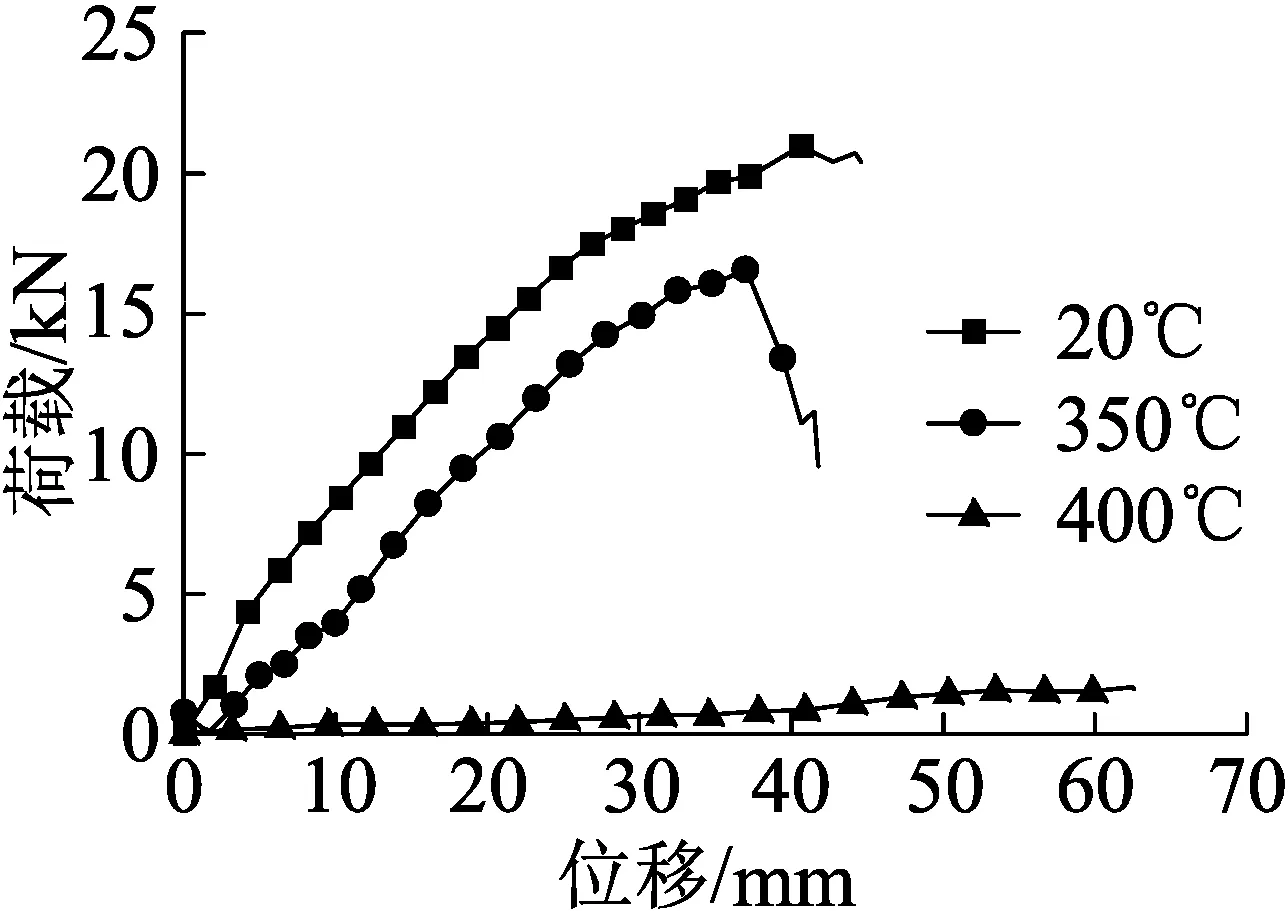
图7 杉木枋荷载位移曲线

2.4 剩余极限强度计算

欧洲EN 1991-1-2[4]采用剩余截面法来计算火灾后木结构的剩余极限强度，该理论认为高温后木枋碳化层已经退出作用，木枋的承载力完全由木枋的有效截面法来决定[21]。

根据木结构规范，杉木枋在三点弯曲过程中，其承受着弯矩和剪力作用。

(1)在弯矩作用下，其公式为[20]

(3)

三点弯曲情况下，弯矩和外荷载的关系为M=Pl/4，将其代入式(3)中，可以得出在弯曲情况下的木枋所受极限荷载为

(4)

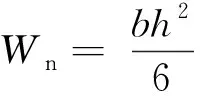
(2)在剪力作用下，其公式为[20]

(5)

三点弯曲情况下，截面剪力和外荷载的关系为V=P/2，将其代入式(5)中，可以得到在剪力作用的极限荷载为

(6)

式中，fv是杉木顺纹的抗剪强度设计值，根据规范，fv取值为1.3 N/mm2。

(3)综合以上两种情况，三点弯曲情况下的木枋的极限荷载为两者较小值。

P=min(Pm,Pv)

(7)

杉木枋高温后的剩余极限荷载与温度关系见图8，可以看出，杉木枋剩余极限荷载随温度升高而降低，加温温度小于350 ℃时，木枋的剩余极限荷载随加温温度增加降低较为平缓；加温温度超过350 ℃后，其剩余极限荷载急速下降，加温温度为400 ℃时，其剩余承载力只有常温情况下的13.4%，当加温温度达到450 ℃时，其剩余承载能力进一步降低，只有常温情况下的5.9%，说明加温温度350 ℃为杉木枋的加温转折点。从图8可以看出，式(7)理论计算结果要小于木枋的试验值，常温情况下两者相差较大，而随着加温温度的升高，两者差距不断缩小。

图8 杉木枋剩余极限荷载与温度关系

3 结论

通过对杉木枋在不同加温温度后的碳化速度和剩余承载力进行分析，结论如下：

(1)杉木枋的碳化速度随加温温度升高而增加，高度方向的碳化速度增长速度更快，高度方向的碳化速度要大于宽度方向的碳化速度。

(2)杉木枋的三点弯矩试验中分为发出响声、出现明显裂纹和碳化层脱落、木枋破坏3个阶段。

(3)高温后杉木枋的荷载位移曲线分为两个阶段，分别为弹性上升阶段和破坏下降阶段。

(4)杉木枋剩余极限荷载随加温温度升高而降低，加温温度350 ℃为加温转折点，当加温温度超过350 ℃，其剩余极限荷载急速下降，在加温温度为400 ℃，其剩余承载力只有常温情况下的13.4%，当加温温度为450 ℃时，其剩余承载能力只有常温情况下的5.9%左右。

(5)采用剩余截面法计算高温后的杉木枋剩余极限强度，在常温情况下两者相差较大，而随着加温温度的升高，两者的差距不断缩小。