基于深度神经网络的航天器姿态控制系统故障诊断与容错控制研究

耿飞龙，李爽，*，黄旭星，杨彬，常建松，林波

1. 南京航空航天大学 航天学院，南京 210016 2. 北京控制工程研究所，北京 100190

航天器在极其复杂、严苛的空间环境下长时间工作，其控制系统执行机构难免出现各种故障。航天器控制系统发生故障，对航天器及航天任务的影响都将是巨大的。调查统计表明，32%的航天器故障来源于航天器轨道姿态控制系统[1]。姿态控制系统的容错控制技术常被用于提高航天器姿态控制的鲁棒性，保证故障情况下航天器姿轨控的精度，对航天器的正常运行尤为重要[2-4]。随着人工智能技术的兴起，基于人工智能技术的姿态容错控制因其良好的适应性以及鲁棒性获得了广泛关注[5-6]。随着航天技术的不断发展，航天任务数量日益增多，相关数据逐渐累积[7]，为深度学习在姿态控制系统故障诊断与容错控制算法的应用提供了充实的数据基础。

基于人工智能技术的容错控制属于主动容错控制范畴。主动容错控制包含故障诊断、操纵律以及可重构的反馈控制器三部分[8-9]。其中，故障诊断是实现容错控制的前提，一直是容错控制领域的研究热点。人工智能技术主要以数据驱动的方式协助故障诊断[10]。Zhao等提出了一种基于支持向量机(SVM)的故障诊断方法，利用主成分分析(PCA)方法生成残差进行姿态控制系统故障分类，然后使用一对一支持向量机分辨传感器和执行机构的故障[11]。Li等通过使用动态神经网络，实现了反作用轮总线电压故障、电流损耗故障或温度故障诊断，并基于此确定了发生故障的反作用轮[12]。Hu等针对以反作用轮为执行器的航天器姿态控制系统，应用核模糊C-均值法设计了能够诊断已知或未知故障的故障诊断器[13]。Valdes等为编队飞行中的脉冲等离子推进航天器设计了一种以动态神经网络为基础的故障诊断方案，通过在线/离线学习的方式对网络进行训练，实现了高准确率的故障诊断[14]。Ahn等从姿态控制系统模拟的多维时间序列数据中提取特征，并使用具有高斯过程的贝叶斯优化算法来优化基于两种生成模型的神经网络参数，最终得到检测航天器姿态控制系统异常和表征故障的方法[15]。Li等通过建立描述电压和温度、电流、压力以及充放电时间等变量之间相关性的神经网络模型，得到一种快速检测航天器蓄电池异常的算法[16]。Huang等为保障未来载人火星探测器在火星进入下降着陆段的控制系统稳定性，采用基于BP神经网络的故障诊断算法，离线训练完毕后的网络能够实时地对故障进行诊断与分离[17]。

在控制器重构机制及控制器设计方面，人工智能技术可通过前馈和反馈的方式实现自适应控制的效果。Eroglu等在飞机姿态容错控制系统中引入了深度循环神经网络以及深度卷积网络，通过分析飞行器状态轨迹，在飞行器执行器或引擎故障时，对自适应控制器的控制参数进行估计。相比于常规自适应控制，该方法极大地提高了控制器协同系数的收敛速度[18]。Sahin等在此工作基础上，不仅利用自适应控制器来控制执行器发生故障的飞行器，同时借助深度卷积网络在风向管故障时估计大气数据[19]。黄怡欣等研究了执行器故障条件下小行星探测器的姿态容错控制问题[20]。Li等使用径向基(RBF)神经网络对多种火星探测器的滑模控制器中的不确定项进行估计，加强了其在火星进入阶段的鲁棒性[21, 22]。Jiang等使用增强学习的方法，在火星进入下降着陆任务的高不确定性条件下，得到全局最优制导律[23]。上述研究分别针对故障诊断和可重构的反馈控制器，运用人工智能技术提高故障诊断及容错控制系统的整体性能，从而实现高鲁棒性的自适应容错控制。在航天器智能故障检测与容错控制领域，目前主流的研究方法是借助于人工智能技术优化故障检测或容错控制系统中的部分环节来提高系统的性能，缺乏利用人工智能技术替代传统姿态控制系统的研究，其技术可行性目前尚未得到验证。当航天器故障诊断及容错控制系统全部替换为深度神经网络等人工智能技术时，如何对神经网络的神经元数量、网络层数、激活函数等进行寻优，还亟待深入研究。

本文针对未来航天器姿态控制系统执行机构的故障诊断与容错控制问题，引入人工智能技术，建立基于深度神经网络的故障诊断与自适应容错控制系统，提高航天器姿态控制系统的控制效率、精度以及鲁棒性。本文假设任务场景是利用冗余控制力矩陀螺保持三轴姿态稳定的空间航天器，当系统内控制力矩陀螺失效后，对故障进行快速诊断识别并控制剩余正常控制器，使航天器实现期望的控制目标。根据万能近似定理(universal approximation theorem)，具备有限隐含层和有限神经元的前馈神经网络能以任意精度拟合任意复杂度的函数[24]。通过运用深度神经网络，对故障诊断映射，控制器再分配映射以及控制器映射进行学习拟合，构建不含任何传统控制器的航天器姿态故障诊断及容错控制系统。随后，对所构建的智能控制器参数进行对比分析，通过优化网络神经元数、网络层数、激活函数等神经网络参数，得到结构最优的深度神经网络姿态容错控制器。通过与传统容错控制器的对比仿真，验证了本文构建的智能姿态容错控制器的可行性，以及在控制效率、精度和鲁棒性方面的优势。

1 航天器姿态控制系统建模

1.1 坐标系定义

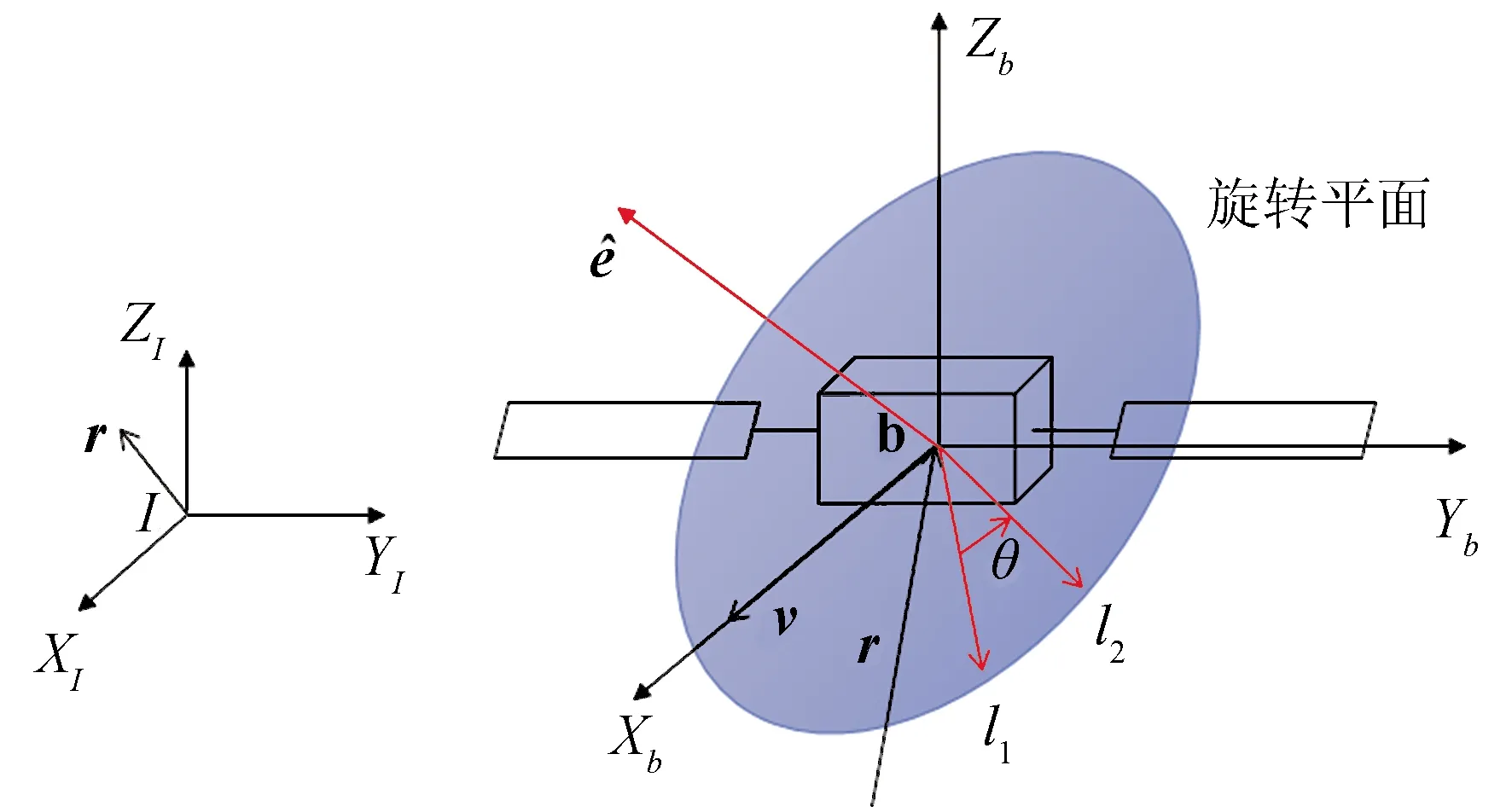
图1 坐标系定义Fig.1 Definition coordinate system

1.2 姿态动力学建模

假设三轴稳定刚体航天器的控制力矩陀螺角动量远小于航天器本体角动量，对航天器本体的影响可以忽略。其中，航天器角速度变化可利用欧拉方程进行描述，其形式如下：

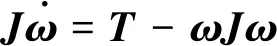
(1)

式中：T为作用于刚体质心上的力矩总和；J为刚体的转动惯量矩阵；ω=[ωx,ωy,ωz]T为姿态角速度。

航天器姿态则利用姿态四元数进行描述以避免奇异。基于四元数的航天器姿态运动学方程如下[25]：

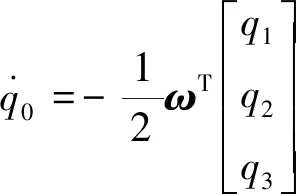
(2)

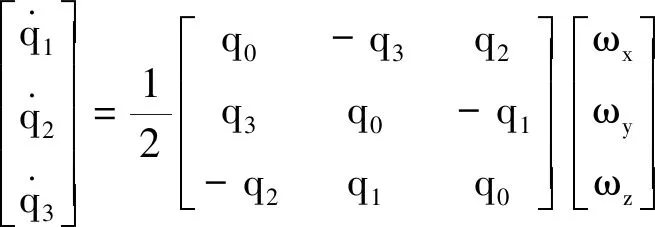
(3)

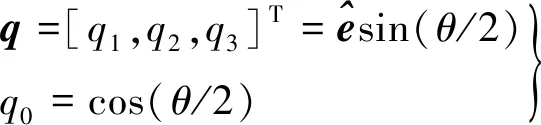
(4)

当航天器动力学参数和初始姿态信息已知时，即可利用以上模型进行数值积分，获得任意时刻的姿态角速度以及姿态四元数。

1.3 控制力矩陀螺故障模型

在航天器控制力矩陀螺发生故障的情况下，陀螺的实际输出信号与其期望产生的输出将会出现偏差。控制力矩陀螺采用三正装一斜装结构，总执行机构数量为4个，安装矩阵如下：

(5)

式中：α为斜装陀螺轴与XbbYb平面的夹角，以陀螺轴在Zb轴方向上分量的符号判断正负；β为斜装陀螺轴在XbbYb平面上的投影与Xb轴的夹角，以该投影在Xb轴方向上分量的符号判断正负。

假设控制力矩陀螺故障为突变故障，通常为陀螺内部某零件发生突发性损坏。该故障类型导致控制力矩陀螺输出发生突变，由正常输出跳变为故障输出。在此基础上，再假设控制力矩陀螺发生空转故障，即控制力矩陀螺完全失效，无法改变自身的转速而导致完全无法输出力矩。

仅考虑单自由度情况下，令to作为力矩陀螺输出的实际控制力矩，同时令tc作为控制器计算所需的控制力矩。为了对该力矩陀螺的故障模型进行建模，这里采用如下式所示的线性模型。其中f为力矩陀螺故障参数。

to=f·tc

(6)

当力矩陀螺无故障时，f设置为1；当力矩陀螺发生故障，则f设置为0。在航天器内有4个力矩陀螺时，将该式变为向量形式以及矩阵形式：

(7)

To=MfTc

(8)

1.4 姿态控制系统构架

在实际任务中，航天器利用姿态控制系统实现姿态调整。姿态控制系统不仅将姿态控制指令转化为控制力矩陀螺的控制信号，同时监测系统的状态，并根据系统运行情况实时调整控制输出。为实现以上功能，姿态控制系统应具备故障诊断、确定控制力矩以及控制力矩分配的能力。航天器姿态控制系统的架构示意图如图2所示。

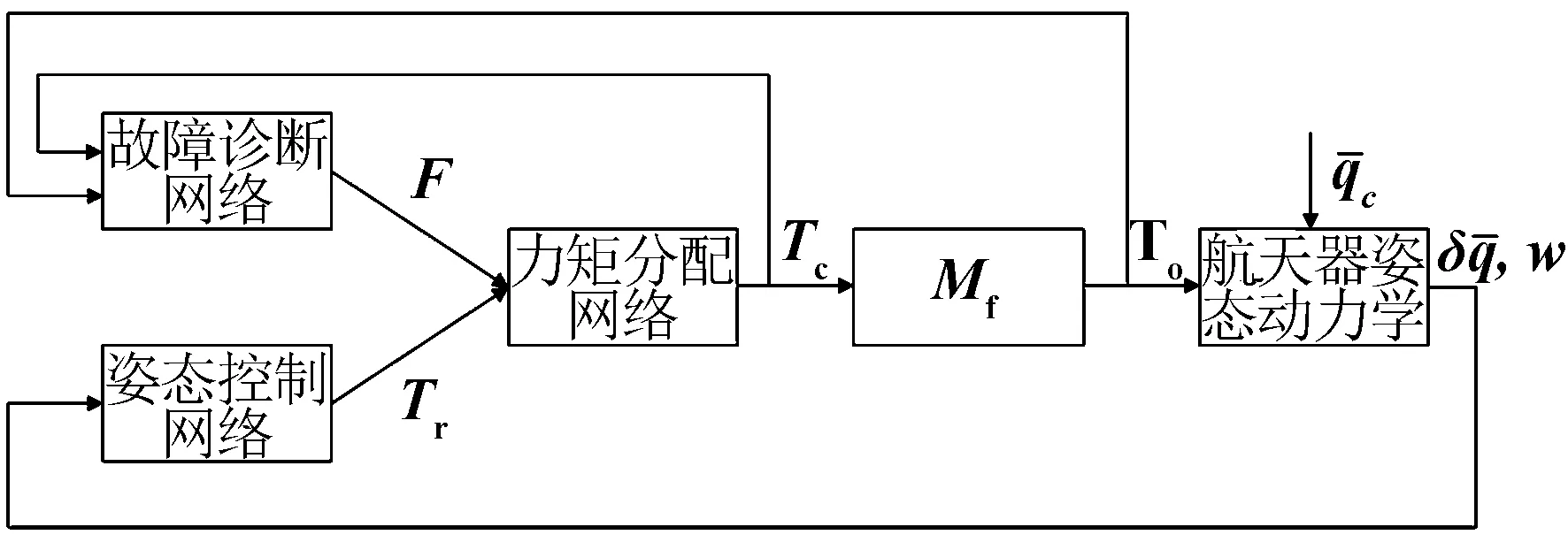
图2 航天器姿态控制系统Fig.2 Spacecraft attitude control system

由于传统控制方法难以满足强非线系统的高精度控制需求，本文通过引入深度神经网络，实现智能故障诊断及容错控制，提高航天器姿态控制效率、精度以及鲁棒性。

2 智能姿态控制系统设计

为提高航天器故障诊断以及容错控制效率，本文基于深度神经网络建立智能姿态控制系统。首先对深度神经网络的结构和激活函数进行简要介绍，再分别建立故障诊断、智能控制以及力矩分配神经网络。

2.1 深度神经网络

2.1.1 网络结构及优化算法

深度神经网络具有极强的非线性拟合能力，理论上能够拟合任意非线性映射。网络节点之间的激活函数影响不同非线性系统的拟合效果。

深度神经网络的基本结构如图 3所示，该网络为全连接神经网络，即每个神经元与上一层网络的每个神经元相连接。输出层可根据不同的任务需求对其结构进行相应的调整，满足映射关系。

利用均方差(MSE)函数作为目标函数，并使用自适应矩估计(Adam)法作为优化算法，对已有数据样本进行离线训练后，最终获得具有目标功能的神经网络算法。

图3 深度神经网络结构Fig.3 Deep neural network structure

2.1.2 激活函数选择

深度神经网络可通过调整神经元之间的激活函数，使网络具备非线性映射的特征，从而使深度神经网络更好地逼近不同的非线性系统。本文通过对比隐藏层神经元激活函数，分析不同激活函数对于网络学习效果的影响。通常使用的隐藏层激活函数有Sigmoid函数、tanh函数以及ReLu函数。其中，Sigmoid函数的公式为：

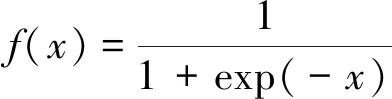
(9)

tanh函数公式为：

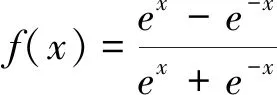
(10)

ReLu函数公式为：

f(x)=max(0,x)

(11)

Sigmoid函数由于其函数饱和使得梯度消失以及并不关于原点中心对称等原因，目前已经较少使用。为代替Sigmoid函数，目前常用tanh函数以及ReLu函数。tanh函数由于其相当于一个中心对称且放大版的Sigmoid函数，有效克服了Sigmoid函数的缺点。而ReLu函数相较于前两种函数，由于其非饱和的特性，能够极大地加速随机梯度下降收敛的过程[26]。因此，在之后的仿真试验中，本文主要对以tanh函数或ReLu函数作为隐藏层激活函数的网络进行学习效果比较。

2.2 故障诊断神经网络

故障诊断神经网络根据期望以及实际控制效果对力矩陀螺工作状态进行判断。通过给定当前以及前若干时刻力矩需求和实际力矩输出的情况，可对当前时刻各个控制力矩陀螺进行故障诊断。考虑到陀螺故障为瞬变故障，本文故障诊断神经网络架设有三个隐藏层以及一个输出层。输出层神经元激活函数为softmax函数[27]，softmax回归模型是logistic回归模型在多分类问题上的推广[28]：

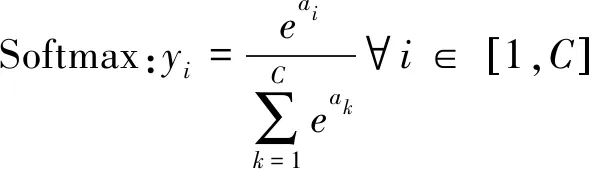
(12)

式中：ai为上一层的第i个输出；C为故障类别数；yi为该类别的概率。最终输出为发生故障概率最大的故障类型yi的序号i。

网络输入为当前时刻各个控制力矩陀螺所需施加的力矩Tc(k)、经过可能的故障控制力矩陀螺后输出的实际控制力矩To(k)以及这两者前一时刻的状态Tc(k-1)与To(k-1)，输出为故障诊断结果F。则故障诊断网络映射可表示为如下形式：

f:Tc(k),To(k),Tc(k-1),To(k-1)→F

(13)

通过以上方式，训练得到用当前及前一个时刻的力矩陀螺的目标输出与实际输出作为输入，来判断力矩陀螺自身状态的故障诊断网络，实现故障类型实时诊断。

2.3 姿态控制神经网络

姿态控制神经网络的主要功能为根据航天器当前状态以及期望控制，对控制输出进行调整，提高姿态控制精度。对于非线性系统的控制问题，LQR可实现高精度的控制效果。航天器姿控系统的线性模型可以写成如下形式：

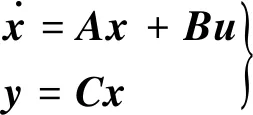
(14)

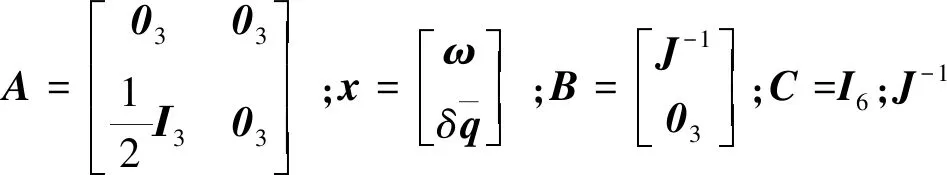
LQR通过搜索最优状态反馈矩阵：

u=-[D,K]x=-Gx

(15)

使得代价函数最小：

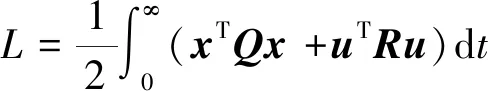
(16)

式中：Q和R都为正定矩阵。

LQR设计的最优控制如下：

u(t)=-R-1BTFx(t)=-Gx

(17)

式中：F为正定矩阵，并且是代数黎卡提方程的解：

-FA-ATF+FBR-1BTF-Q=0

(18)

由文献[25]可以得到最优控制：

u(t)=-[R-1J-1F11,R-1J-1F12]x

(19)

并且在该控制条件下，航天器的姿态仍然可以保持稳定[25]。

(20)

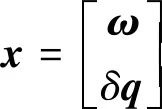
(21)

(22)

通过输入当前角速度以及姿态误差四元数的复数部分，网络即可输出三轴控制力矩。

2.4 力矩分配神经网络

力矩分配神经网络的主要功能为在确定了航天器当前控制力矩需求的情况下，结合各个控制力矩陀螺的状态进行执行机构分配，实现鲁棒容错控制。当力矩陀螺处于不同状态时，姿态控制系统可利用冗余机构对控制输出进行分配，实现自适应容错控制。控制分配问题描述如下：一个动态系统具有输入矩阵B∈Rn×l，且l>n，即系统状态数量小于可施加的控制数量，具有冗余控制量。但每个控制量都具有界限约束(即umin和umax)。对于所需控制量md。则当冗余控制实现所需控制量的同时，控制消耗达到最优，即可实现最优控制，其形式如下：

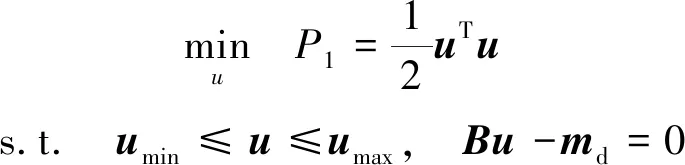
(23)

若控制不能满足等式条件约束，则应最小化其误差：

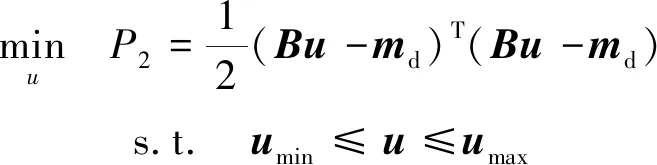
(24)

作为训练样本，本文基于冗余机构的力矩分配算法采用改进伪逆重分配算法[29]。传统伪逆矩阵分配算法在没有破坏不等式约束的情况下时，得到力矩分配结果，其形式为：

u=BT(BBT)-1md≡B+md

(25)

当系统输出u不符合约束时，可利用改进伪逆重分配算法求解符合约束的力矩，更新最优力矩分配方案。改进伪逆重分配算法的流程如下：

3)将输出分为饱和输出us以及冗余输出ur，将us的值设定为其对应的极限值。同样将两者对应的控制矩阵也分为饱和矩阵Bs和冗余矩阵Br；

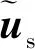
5)如果ur=null，则转到第7步；

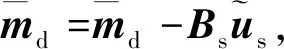
8)最终得到的u即为符合不等式约束的再分配输出值。

当航天器控制力矩陀螺发生空转故障时，故障识别网络检测并识别出故障的发生以及故障类型，将故障类型信号发送给力矩分配神经网络。力矩分配网络结合所需力矩，对输出信号重分配。对故障陀螺发出需求零力矩输出的控制信号，对其余正常陀螺发送按照所学习操纵律进行重分配后的所需力矩控制信号。

基于改进伪逆重分配算法获得训练样本，对深度神经网络进行训练。其中，网络中含有数个隐含层，每个隐藏层含有若干个神经元，激活函数、具体隐藏层层数以及神经元数目将在仿真分析中给出。在生成训练样本时，通过输入设定好的故障诊断结果F得到对应的输入矩阵B∈Rn×l，并使用设定好的所需力矩Tr的序列，利用该算法生成控制力矩分配输出作为网络的输出训练数据Tc。最终学习映射：

f:Tr,F→Tc

(26)

由于该力矩分配算法需要进行矩阵求逆运算，且在超过控制量界限约束时需进行迭代运算，神经网络方法则无此需求，因此理论上设计合理的力矩分配神经网络可减小分配过程的运算量。

3 仿真分析

本文对上述系统进行了仿真试验。仿真试验包含两部分：对于3种网络的训练以及最终容错姿态控制系统的仿真。仿真环境：CPU:i7-8750H，GPU:GTX1060(6G)，matlab2016a，python3.6，tensorflow1.12。

3.1 故障诊断及姿态控制深度神经网络训练

3.1.1 故障诊断神经网络训练结果

利用Matlab按照各个故障状态时的故障力矩陀螺矩阵，各陀螺通过随机数生成随机力矩向量，并通过故障力矩陀螺矩阵得到三轴实际输出力矩向量。得到16万组各种故障情况下的力矩输入输出数据样本。从数据集中随机选取10%的样本作为测试集，剩余90%将作为训练集。在训练集中再抽取20%的样本作为训练时的验证集，以供训练过程中验证其训练效果。网络设定含有3个隐藏层，每一层均含有64个神经元。将数据集带入网络进行训练，每完成一次训练集的训练后对其中的验证集进行测试，当验证集准确率经过10次迭代学习后未减小时，停止训练。设置最大训练次数100次。训练完毕后使用测试集数据对其分类准确率进行验证。

故障诊断网络的准确率随训练次数的变化如图 4所示。在经过约60次的训练后，准确率几乎不再上升，此时停止训练。可以看到网络在经过多次迭代之后，其识别准确率已经可以达到较高水平，约97%。

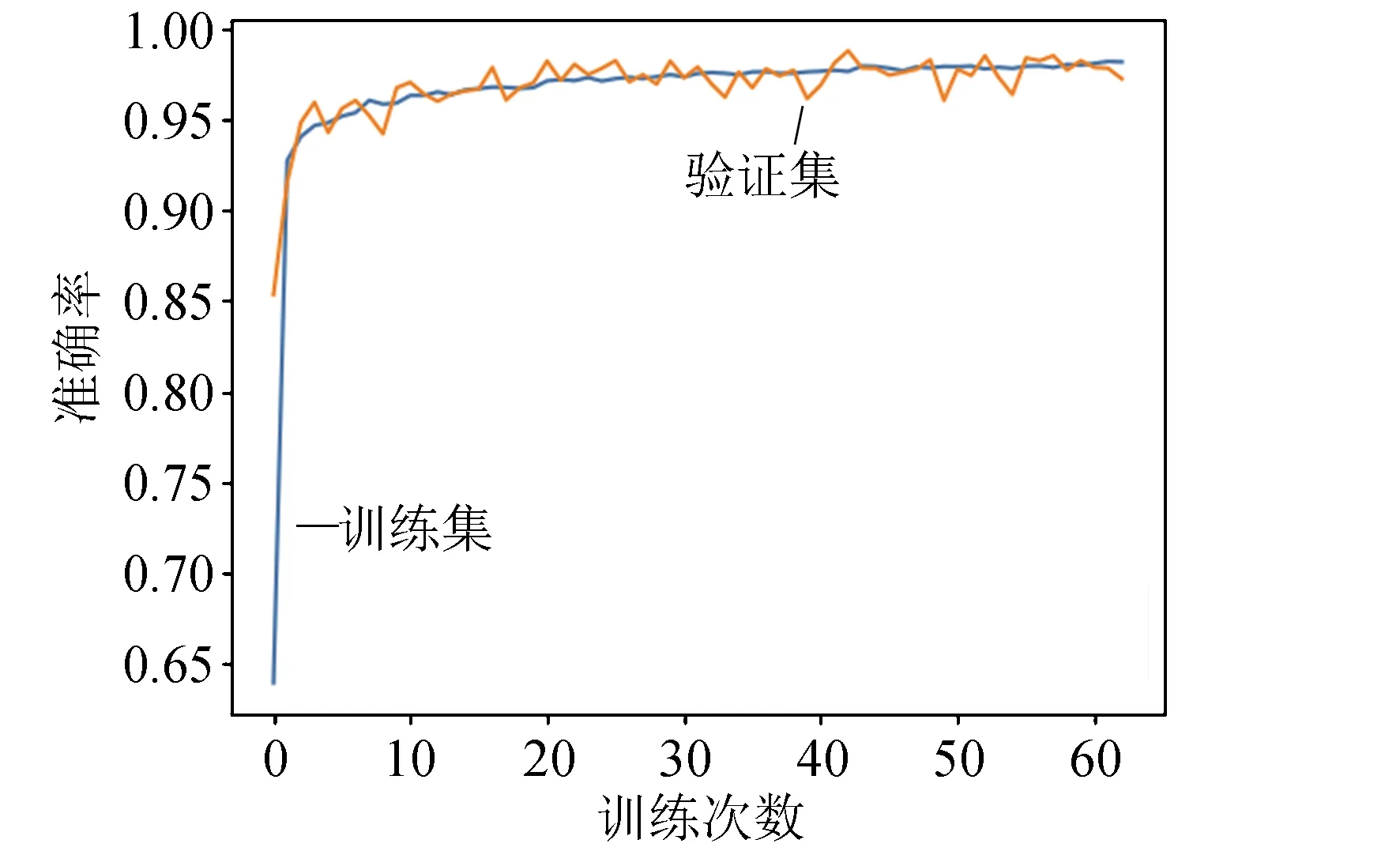
图4 故障诊断神经网络训练时准确率变化Fig.4 Accuracy change for fault diagnosis neural network in training

3.1.2 姿态控制神经网络训练结果

首先通过仿真程序生成了约200万组仿真姿态控制数据，每个数据都为一组角速度向量和三轴所需力矩向量。本文利用Matlab搭建控制器模型，各轴角速度当取值绝对值在[0.02,0.2]rad/s区间内时，以0.06 rad/s作为间隔，当取值绝对值在[0,0.02]rad/s区间内时，以0.006 rad/s为间隔；在每个角速度情况下，随机生成1 000个姿态误差四元数作为四元数样本，用其向量部分与角速度向量合并为网络输入向量。LQR状态反馈矩阵如下：

计算出每个网络输入对应的所需三轴力矩向量。从数据集中随机选取10%的样本作为测试集，剩余90%将作为训练集。在训练集中再抽取20%的样本作为训练时的验证集，以验证其训练效果。随后将数据代入网络中进行训练，每完成一次训练集的训练后对其中的验证集进行测试，当验证集均方差经过10次迭代学习后未减小时，停止训练。设置最大训练次数200次。训练完毕后使用测试集数据对其进行验证。

深度神经网络选择如表 1所示的6种备选结构，全部都先后采用不同的隐藏层激活函数进行试验对比，综合比较得出最优结构以及最佳隐藏层激活函数。

表1 姿态控制神经网络结构参数

训练结果如表 2所示。可以看到，tanh激活函数的网络在此环境下的训练集均方差普遍比ReLu激活函数低一个数量级，在测试集中，tanh激活函数网络组的均方差也普遍小于ReLu组。在同种激活函数的网络之中，tanh组的训练效果随着网络结构的简化而提高；ReLu组则是编号2与编号4型网络出现了局部最优训练效果。可以认为tanh组最优结构在编号6型或更简化的结构中，而ReLu组最优结构则在编号2和编号4型相近的结构中。由tanh组网络训练效果与网络结构复杂度相反的结果可以得出，该组普遍存在过拟合的情况：相较于单层128神经元的网络，单层64神经元的网络训练集以及测试集结果全面领先，且层数较少的网络能够在一定程度上避免过拟合。

表2 姿态控制神经网络训练结果

在本测试条件下，tanh激活函数的6号网络能够得到最优的精度，而ReLu激活函数的2号网络能达到该激活函数下的最高精度。最终选择tanh激活函数的6号网络作为下一步试验的姿态控制网络。

3.1.3 力矩分配神经网络训练结果

首先通过仿真程序生成了约160万组仿真力矩分配数据，每个数据都为一组三轴所需力矩向量、故障诊断结果和各个力矩陀螺的输出力矩指令。通过Matlab中事先建立的先验知识力矩分配算法，分别在[-10,-1]∪[1,10](N/m)、[-1,-0.1]∪[0.1,1](N/m)、[-0.1,-0.01]∪[0.01,0.1](N/m)和[-0.01,0.01](N/m)区间内，以2 N/m、0.2 N/m、0.02 N/m和0.002 N/m为间隔，生成操纵律样本，且每种故障状态均重新生成一次，最终得到在每种故障状态和每种三轴力矩需求状态下，各个力矩陀螺的输出力矩指令。将该组数据作为训练集，在训练集中抽取20%的样本作为训练时的验证集，以供训练过程中验证其训练效果。测试集重新按各轴力矩需求以5.1 N/m为间隔，从-70 N遍历到70 N，且每种故障状态均重新生成一次。随后将数据代入网络中进行训练，神经网络有4种备选结构，其参数如表 3所示，先后都采用不同的隐藏层激活函数进行试验对比。每完成一次训练集的训练后对其中的验证集进行测试，当验证集均方差经过10次迭代学习后未减小时，停止训练。设置最大训练次数100次。训练完毕后使用测试集数据对其进行验证。

表3 力矩分配神经网络结构参数

训练结果如表 4所示。可以看到所有网络训练到最终，验证集均方差数量级都在个位数级，测试集均方差数量级也基本相同。ReLu激活函数网络的验证集均方差以及测试集均方差均要小于tanh激活函数网络。同激活函数网络当中，ReLu组各个结构的网络训练结果相差并不大。故选择ReLu 激活函数的3号网络作为下一步试验的力矩分配网络。

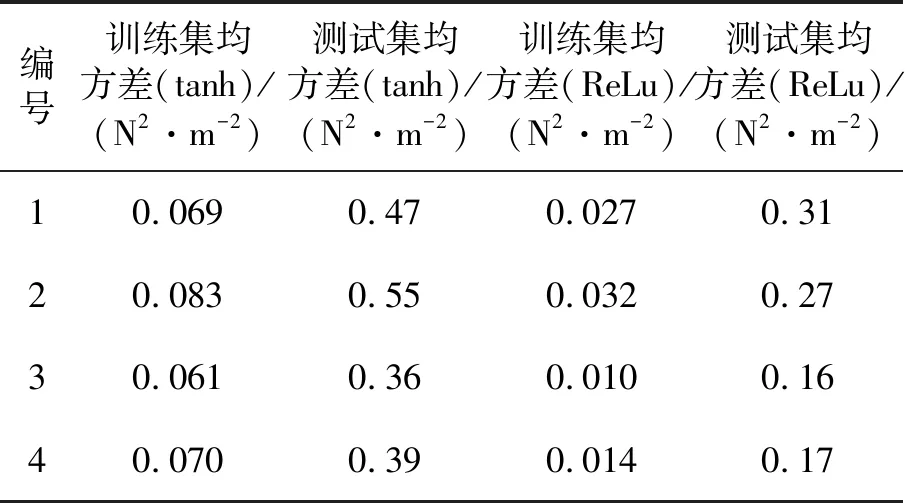
表4 力矩分配神经网络训练结果

3.2 智能姿态容错控制系统仿真

仿真场景为航天器在正常运行状态时，突发力矩陀螺故障。在一定范围内随机的初始角速度下，若航天器能够实现从当前姿态四元数转移到目标姿态四元数，则认为该姿控系统有效。控制力矩陀螺安装矩阵为：

航天器惯量矩阵为：

仿真步长为0.01 s，进行仿真。

场景1：令各轴初始角速度在[-0.2,0.2](rad/s)内随机取值，令故障时间在[0,50]s内随机取值，仿真时长定为100 s，令故障种类为4个控制力矩陀螺中随机一个发生空转故障。其中选取初始角速度为[0.1,-0.15,0.1](rad/s)，初始姿态四元数为[0.035 7, 0.848 6, 0.493 0, 0.188 6]，目标姿态四元数为[ 0.678 7 , 0.556 5 , 0.356 1, 0.320 7]，在10 s时发生Xb轴控制力矩陀螺故障的情况进行仿真模拟绘图。仿真结果如图5～9所示。

图5 场景1下三轴角速度Fig.5 Three axes angular velocity under case 1

图6 场景1下三轴控制力矩大小Fig.6 Three axes control moment under case 1

图7 场景1下各控制力矩陀螺输出力矩Fig.7 Output torque of each reaction wheel under case 1

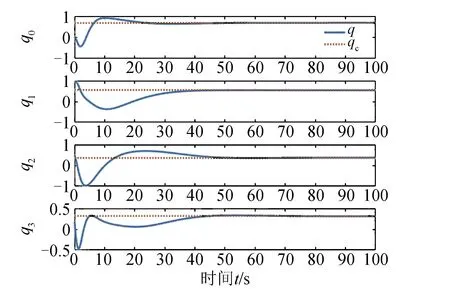
图8 场景1下姿态四元数变化情况Fig.8 Attitude quaternion variation under case 1

图9 场景1下姿态四元数末状态误差Fig.9 End state error of attitude quaternion under case 1

根据仿真结果可知，航天器在第10 s前，图7中所有力矩陀螺均正常运行，图5中各轴角速度逐渐减小，图8中姿态四元数逐渐收敛至目标姿态四元数；航天器在第10 s时，图7显示Xb轴力矩陀螺输出T1突然减小至0，姿控系统随即对输出力矩进行再分配。为补偿原Xb轴控制力矩减少的量，冗余陀螺需要增加其在Xb轴上的控制力矩分量，Yb轴与Zb轴陀螺也需要补偿因冗余陀螺输出变化而导致的自身轴方向上控制力矩的变化。Yb轴与Zb轴陀螺均减小输出，冗余陀螺输出增加。最终，实现航天器角速度回0，图9也显示姿态四元数与目标姿态四元数基本吻合，证明该容错姿控系统有效。

在此基础上，进行1 000次蒙特卡洛仿真，最终得到的四元数平均绝对误差，如表5所示。

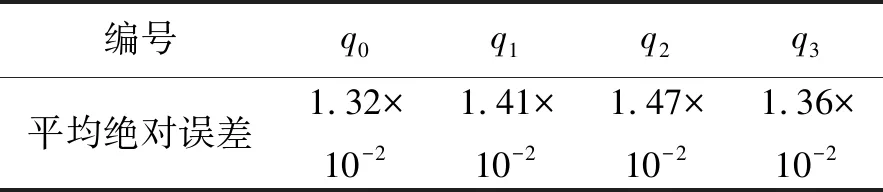
表5 蒙特卡洛仿真四元数平均绝对误差

可以看出1 000次的蒙特卡洛仿真四元数绝对误差值都在10-2量级，该姿控系统能够在单一控制力矩陀螺故障的情况下，令航天器姿态稳定于目标姿态。

场景2：故障场景假定为全部力矩陀螺的其中随机两个力矩陀螺发生空转故障，其余正常运行；仿真时长定为200 s，其他条件与场景1相同。选取其中两次不同的子场景进行仿真分析，其初始角速度、初始姿态四元数和目标姿态四元数均相同，分别为：[0.1,-0.15,0.1](rad/s)、[0.0357, 0.8486, 0.4930, 0.1886]、[0.6787, 0.5565, 0.3561, 0.3207]。仿真1在20 s时，Xb轴与Yb轴力矩陀螺发生空转故障；仿真2在20 s时，Xb轴与Zb轴力矩陀螺发生空转故障。两组仿真中各个力矩陀螺输出与姿态四元数如图10～13所示。

在仿真1中，Xb轴与Yb轴力矩陀螺输出力矩20 s之后归零，但是姿态控制系统仍能够维持航天器姿态稳定，并使姿态四元数接近目标姿态

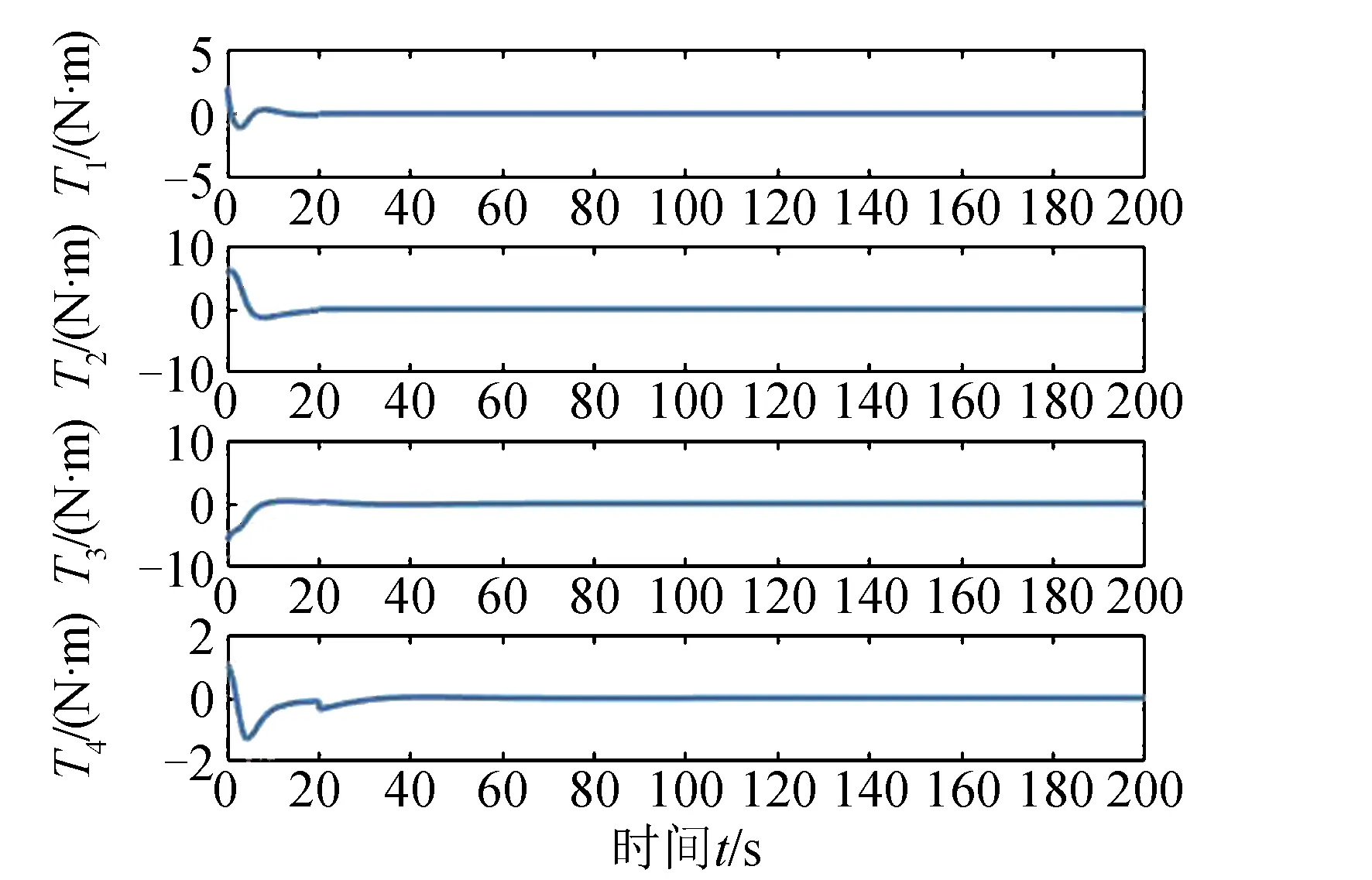
图10 场景2下仿真1各控制力矩陀螺输出力矩Fig.10 Simulation 1 output torque of each reaction wheel under case 2

图11 场景2下仿真1姿态四元数变化情况Fig.11 Simulation 1 attitude quaternion variation under case 2

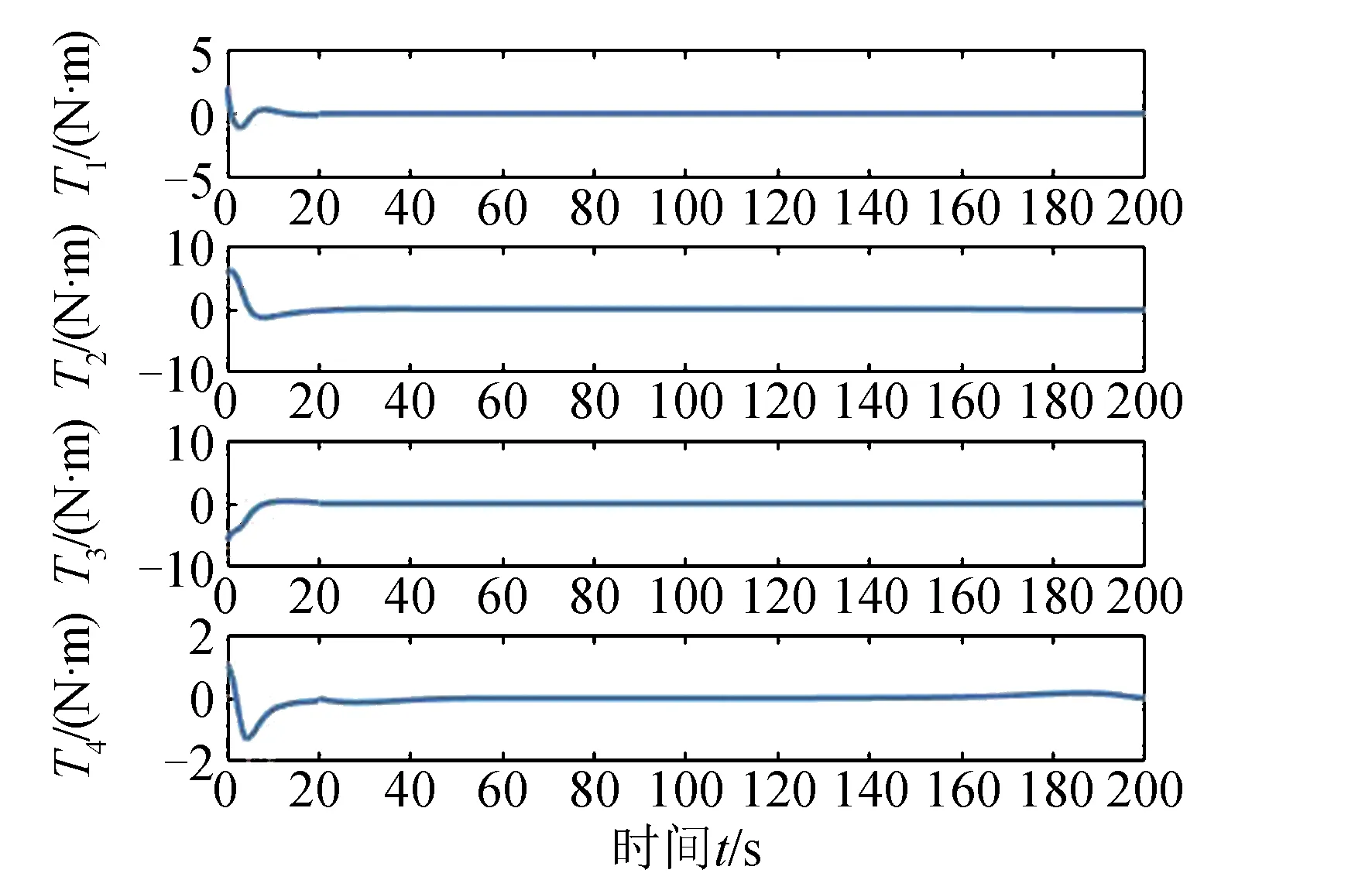
图12 场景2下仿真2各控制力矩陀螺输出力矩Fig.12 Simulation 2 output torque of each reaction wheel under case 2

图13 场景2下仿真2姿态四元数变化情况Fig.13 Simulation 2 attitude quaternion variation under case 2

四元数。而在仿真2中，冗余控制力矩陀螺输出在20 s过后无法稳定，仍保持着小幅度的震荡，姿态四元数因此难以保持稳定、无法收敛于目标姿态四元数。在场景2中，容错姿态控制系统在一定条件下，能够令航天器到达并稳定在目标姿态。但也存在一些情况，航天器无法到达目标姿态，航天器姿态系统已到达其控制能力的极限，控制量自由度小于被控状态自由度。

对于导致仿真1中能控制和仿真2中无法控制两种结果的原因分析如下：仿真1中发生故障前，Xb轴与Yb轴力矩陀螺输出力矩的符号相同，冗余陀螺输出力矩中对应Xb轴与Yb轴的分量符号也相同。发生故障后，经由控制分配网络的分配，由于冗余陀螺也可以在Xb轴与Yb轴输出同号的控制力矩，无故障轴有另一正常陀螺进行控制力矩补偿，故在一定程度上冗余陀螺代替两故障陀螺输出仍可以使得航天器姿态稳定。但在仿真2中，Xb轴与Zb轴力矩陀螺输出力矩符号为异号，冗余陀螺无法同时在两轴上输出异号的控制力矩，被控量因此逐渐发散，最终姿态四元数无法收敛于目标姿态四元数。两仿真在同初始条件下，前20 s的航天器状态完全相同，但因故障类型不同，在该时刻所需的控制力矩补偿也会因情况而异。这对于安装方式已经固定的冗余陀螺来说，只有所需的控制补偿与其输出类型相似(此仿真中为输出的正负号相对应)的情况下，才能使航天器稳定在目标姿态。此外，神经网络输出误差带来的不确定性，也会导致航天器姿态稳定难度增加。

4 结束语

本文基于深度神经网络设计了航天器姿态控制系统故障诊断与容错控制方法。利用多个训练完备的深度神经网络，替换故障诊断、控制器再分配以及姿态控制部分，得到不含任何传统控制器的航天器故障诊断及容错控制器。当单一控制力矩陀螺出现故障时，故障诊断网络利用自身强大的分类能力对故障类型进行识别，姿态控制网络根据当前姿态和目标姿态快速输出相应的控制信号，再利用力矩分配网络对控制力矩再分配，使航天器姿态收敛并稳定在目标姿态附近。最终仿真结果表明，在仅出现单个力矩陀螺空转故障的情况下，本方法能令航天器姿态四元数的差值保持在0.01左右；当在两个力矩陀螺出现空转故障时，本方法仅能够在一定条件下令航天器姿态到达并稳定于目标姿态。各神经网络理论上应该可以学习任意控制律并实现相应的控制效果。当前本文仿真中的系统故障模型较为简单，复杂模型下的故障诊断及容错控制仍待后续进一步研究。