地球同步轨道卫星混合推进转移轨道特性分析

段晓闻，祁瑞，* ，王敏

1. 北京理工大学 宇航学院，北京 100081 2. 中国空间技术研究院，北京 100094

燃料消耗是开展轨道转移任务优化设计的重要约束。相比于传统化学推进，电推进因其比冲高的特性，能够大大降低燃料消耗，为任务提供更大的有效载荷[1-4]。然而，由于推力较小，电推进任务往往要求更长的转移时间。如果将化学推进和电推进两种方式结合，则有可能在减少燃料消耗的同时，加快轨道转移时间，在燃料消耗和转移时间之间达到折中。这种推进方式被称为化学-电混合推进。采用混合推进，不仅拓宽了GEO任务设计的可行空间，也具有燃料消耗低、转移时间短、发射窗口不敏感的优势。在混合推进轨道的设计过程中，全电推进和全化学推进作为混合推进的特殊形式，为任务解算提供了可参考的边界。

到目前为止，已经有学者在化学-电混合推进转移轨道优化设计方面开展了研究，并做出了重要贡献。1962年Edelbaum率先分析了混合推进的设计方法，此方法仅给出了初步的概念，并没有对具体任务开展针对性分析[5]。随后，Oleson等基于NASA Glan开发的SEPSPOT Sachett工具包开展了混合推进转移设计[6]。Mailhe等改进了从近地轨道到地球同步赤道轨道的共面转移方案[7]，整个过程先由电推进推离LEO，后到达某高度采用化学推进进行两次霍曼转移，最后经由电推进注入GEO。文中对整体辐射剂量的影响作了表征，并在系统层面对混合推进航天器任务进行了初步设计。Oh等设计了两阶段系统和三阶段系统，但后续有学者指出其三阶段的设计中没有考虑电推进发动机工作后再施加脉冲推力的冲击影响[8]。Kluever对GEO轨道转移的化学-电混合推进方案进行了分析[9]，并开发了一种可以快速开展大推力和电推进轨道转换权衡的算法[10]，文中将各种LEO-GEO的混合推进轨道转移数据数值化，大大提高了解算速率。然而，该方法由于简化条件太多，只适合轨道的初步设计。杨傅等采用高斯伪谱法对化-电混合推进展开研究，得到了一种快速解算算法[11]。Ceccherini和Topputo等在系列文章中创新地引入二维过渡轨道搜索网格解算混合推进轨道[12-15]，本文的相关研究就以此为基础。

在混合推进轨道优化问题中，过渡轨道的确定是关键，从过渡轨道到目标轨道的小推力转移段的设计优化是难点。本文以从近地轨道到地球同步轨道的混合推进转移任务为背景，以Ceccherini和Topputo等开发的过渡轨道搜索网格算法模型为基础，开展混合推进转移轨道优化和分析。过渡轨道将整个GEO转移轨道分为3部分：化学推进段、过渡轨道段以及电推进段，其中化学推进阶段采用Lambert转移方法解算，电推进阶段采用混合法解算。

1 优化问题描述和模型介绍

在进行优化前，首先需要明确混合推进中化学推进和电推进两者的开机序列。Oberth效应指出，在速度较高的地方进行化学推进轨道机动较为有利，即化学推进在中心天体附近应用效率较高，而电推进则在远离中心天体的位置的应用效率较高[16]。另外，对于混合推进轨道转移，先进行电推进后再进行化学推进会对卫星造成瞬时冲击影响，严重者可能损坏太阳翼[12]。因此，在近地轨道首先开启化学推进发动机，使卫星变轨进入轨道高度较高的过渡轨道，卫星在过渡轨道上进行调整，展开太阳翼，然后开启电推进发动机完成剩余变轨任务。整个混合推进转移轨道分为3段：化学推进转移段、电推进转移段以及连接两者的过渡轨道段，如图1所示。化学推进段的推力大，作用时间短，在本文中取最省燃料解；电推进段的推力小，耗时长，取时间最优解。

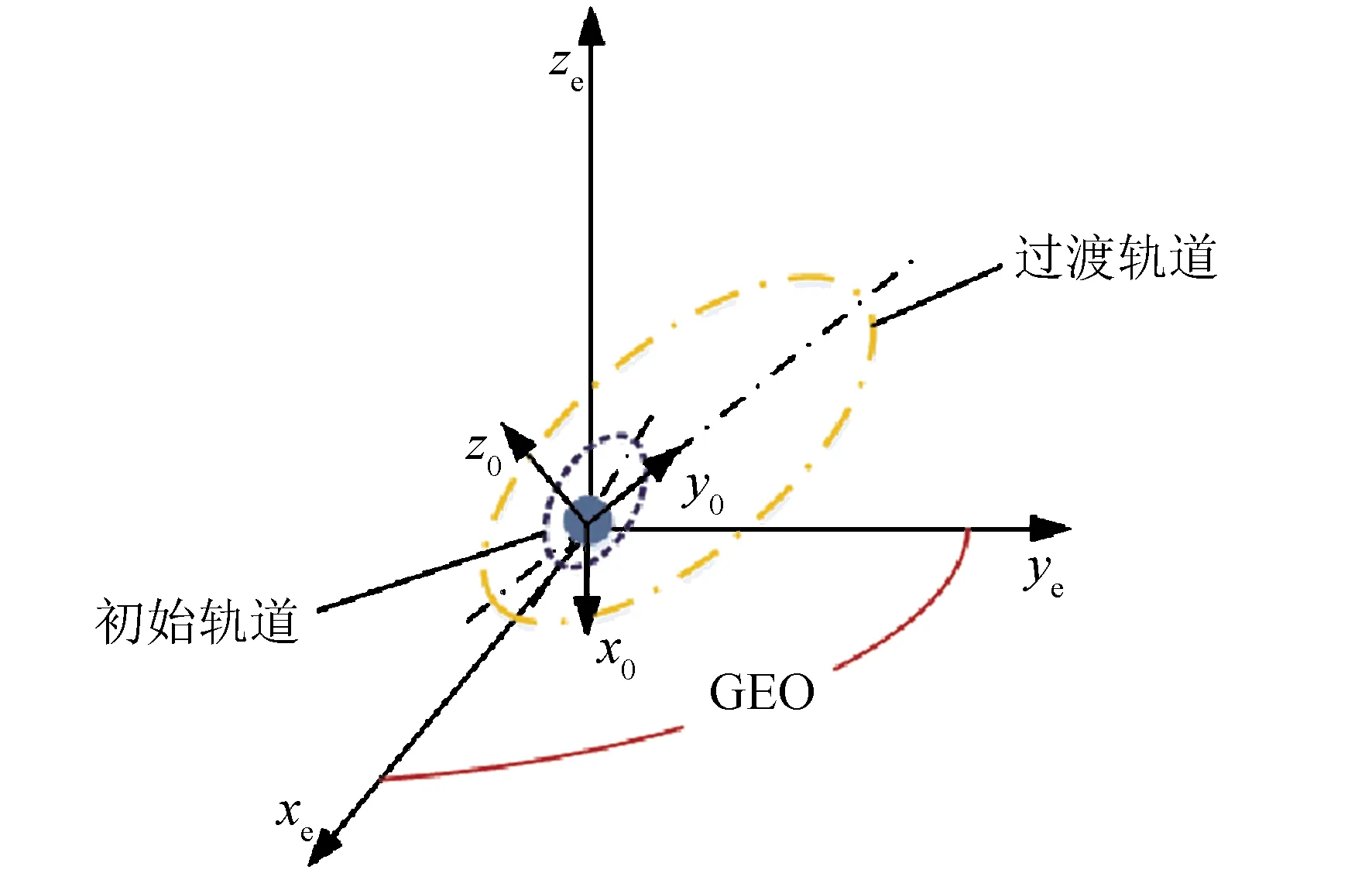
图1 化学-电混合推进轨道示意Fig.1 Schematic diagram of combined chemical-electrical propulsion

在化学推进段，一般采用霍曼转移能够求解同平面共拱线两轨道之间的转移。本文考虑了轨道倾角差，即需求解异面轨道间的转移问题，因此采用Lambert转移方案，解算速度增量时使用Gooding的Lambert问题解[17-18]。给定初始轨道上卫星的位置，遍历初始轨道等待时间和轨道转移时间两个参数，便可寻优得到最优脉冲转移段。

在电推进转移段，由于笛卡尔坐标系描述的卫星状态矢量是快变量，而Kepler轨道六要素可能存在奇异问题，因此本文采用改进的春分点轨道要素(p,ex,ey,hx,hy,L)建立带J2摄动项的电推进段的动力学方程[19]。基于庞特里亚金极大值原理，将最优控制问题转化为两点边值问题，用混合法求解最省时间问题。

矩阵形式的动力学表达式为[20-21]：

(1)

对应的Hamilton函数表示为：

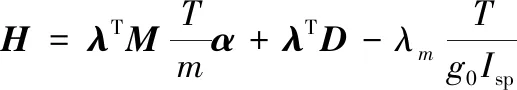
(2)

式中：λ=[λp,λex,λey,λhx,λhy,λL]T，为引入的改进春分点协态变量；λm为质量对应的协态变量。

最省时间问题可表述为如下两点边值问题：

(3)

采用序列二次规划和混合法进行优化解算。

本文中轨道优化任务的初始轨道为倾角28.5°、近地点高度200 km、远地点高度2 000 km的椭圆轨道，默认其他轨道根数为零。目标轨道为GEO轨道。假设卫星的初始质量为1 500 kg，除轨道转移外无质量损失。

2 解算模型

2.1 格点法

如果将过渡轨道参数(近地点距离、远地点距离、轨道倾角)作为优化变量，与电推进段的协态变量一起优化，将导致优化变量多、算法难以收敛的问题。本文采用Ceccherini和Topputo等提出的格点法，将过渡轨道在搜索域内格点化，针对每条过渡轨道开展混合推进转移轨道优化解算，然后在整个解空间中根据任务约束寻求最优解。

以近地点和远地点距离表示的搜索网格如图2所示，横轴表示过渡轨道近地点距离Rp，纵轴表示过渡轨道远地点距离Ra，第一象限内每一个“”符号代表一条过渡轨道。对于是否在网格划分中考虑轨道倾角i和近地点幅角ω等变量，本文第2.3小节将开展讨论。

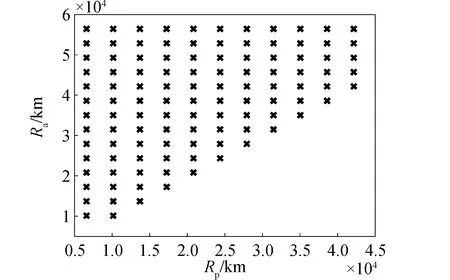
图2 搜索网格示意Fig.2 Search grid diagram

2.2 逻辑构架

搜索网格中的每一个格点对应一条过渡轨道，顺序求解化学推进段与电推进段，最后将结果整合形成完整混合推进转移轨道。重复这一过程，直到遍历采样网格中的所有格点。解算流程如图3所示[12-15]。

2.3 搜索网格简化

第2.1小节的搜索网格示意中仅对近地点距离和远地点距离进行了划分，是否应当引入轨道倾角和近地点幅角这两个维度，还需要进一步的分析讨论。本节将对混合推进轨道优化设计中轨道倾角和近地点幅角变化带来的影响进行分析，用以最终明确搜索网格中的优化变量。

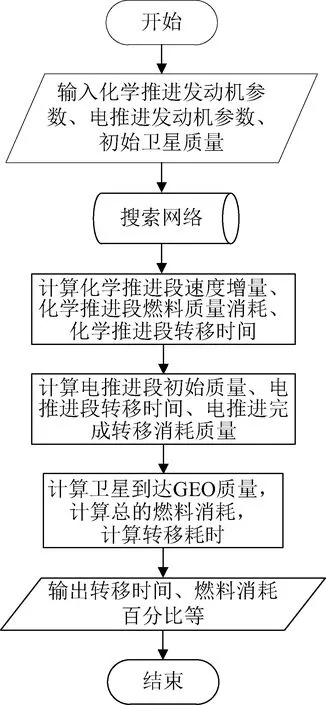
图3 解算流程Fig.3 Solution flow chart

具体使用控制变量的方法，首先保持近地点幅角不变，令搜索网格中过渡轨道倾角变化，观察其对整个混合推进轨道设计结果的影响；然后固定过渡轨道倾角，使近地点幅角变化，同样观察其对混合推进轨道的影响。

(1)轨道倾角变化对转移轨道设计的影响

在下面的仿真中化学推进段取Isp1=300 s；电推进段Isp2=3 000 s，电推进发动机提供的推力为Tmax=0.2N；初始轨道取为近地点高度200 km、远地点高度2 000 km的椭圆轨道，轨道倾角28.5°，近地点幅角取为0°，其他轨道要素皆假设为零。

由于初始轨道倾角为28.5°，目标GEO轨道倾角为0°，因此不同的过渡轨道倾角对应于化学推进段和电推进段对轨道倾角改变的不同贡献。例如，当过渡轨道倾角为28.5°时，在化学推进段不进行轨道倾角调整，倾角调整完全由电推进段完成；当过渡轨道倾角为9.5°时，轨道倾角先由化学推进调整19°，再由电推进调整9.5°。图4～图8中标注的轨道高度为偏心率相同(e=1/11，Ra/Rp=6/5)，近地点半径依次增大至GEO高度的一系列过渡椭圆轨道的近地点高度Rp。例如，x轴上近地点距离为10 000 km的点，表示近地点距离10 000 km，远地点距离12 000 km的椭圆轨道。

由齐奥尔科夫斯基方程Δv=ve×ln(m0/mf)，速度增量与发动机有效排气速度ve和燃料质量消耗m0/mf有关，而有效排气速度可表示为ve=Ispg0。在本文中，脉冲段比冲与电推进段比冲是不同的，所以在燃料消耗问题中仅考察轨道转移的总速度增量不够严谨。本文将速度增量转为始末质量比mGEO/m0能得出更直观的结果，如图4所示。总转移时间Ttol随过渡轨道倾角i和过渡轨道高度的变化曲线，如图5所示。

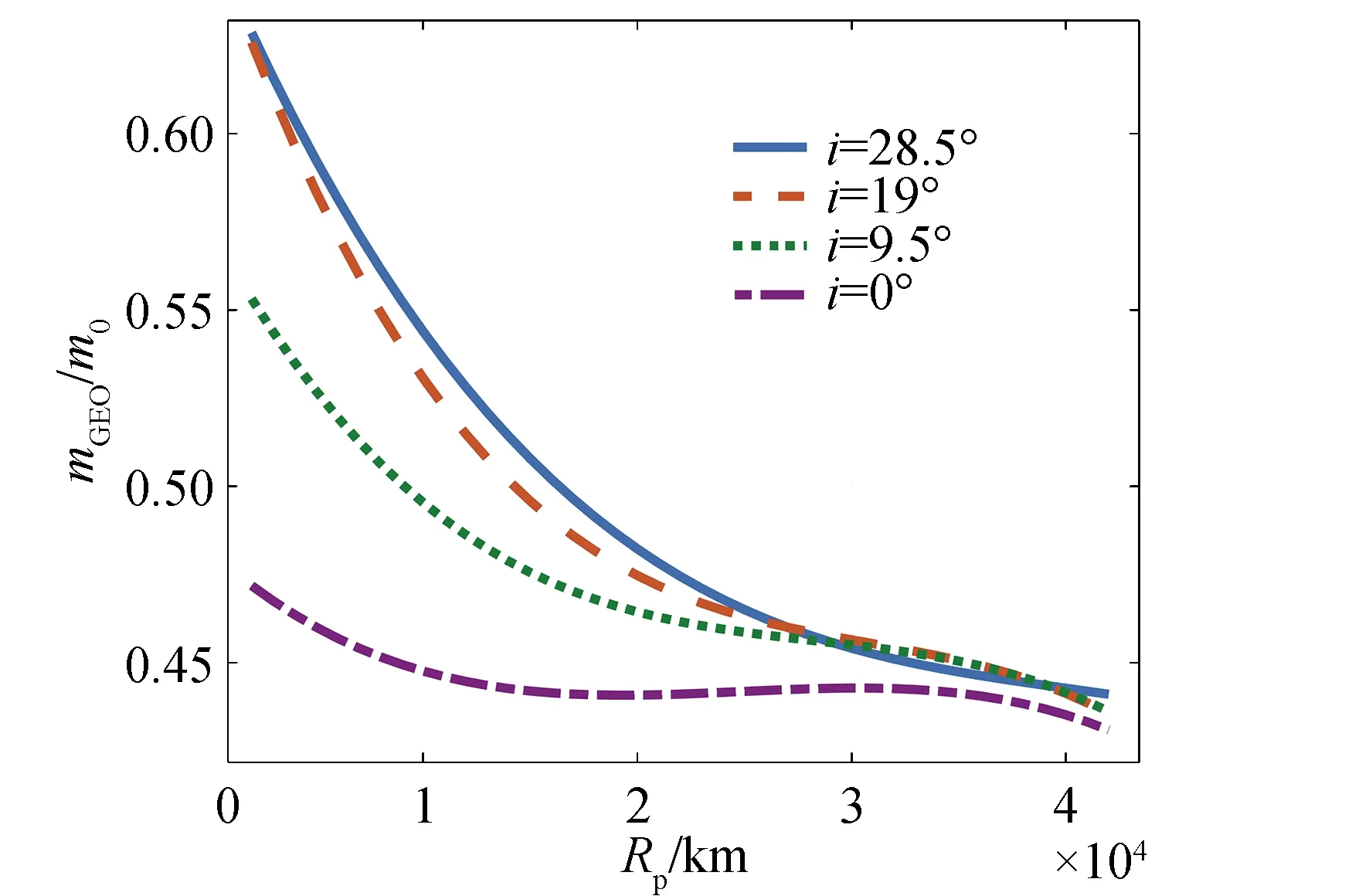
图4 始末质量比值随过渡轨道倾角和 轨道高度的变化曲线Fig.4 The curve of beginning-to-end mass ratio with the inclination and the perigee altitude of searching orbit

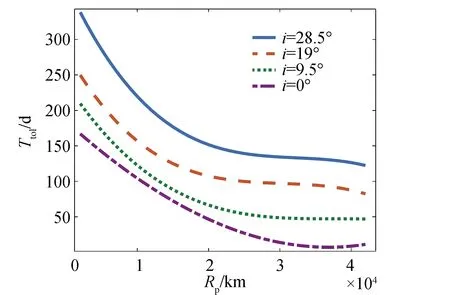
图5 总转移时间随过渡轨道倾角和 轨道高度的变化曲线Fig.5 The curve of transfer time with the inclination and the perigee altitude of searching orbit

图4和图5刻画了过渡轨道高度和轨道倾角改变时卫星的始末质量比值和转移时间的变化规律，其中m0为卫星在初始轨道的质量，mGEO为卫星到达GEO的质量。图4中，纵轴为整个转移过程末质量与初质量比值mGEO/m0。该比值较大时，说明轨道转移消耗的燃料少，传送至GEO的质量多；反之，说明轨道转移消耗的燃料多。由图4可见，实线最左端出现了最高的mGEO/m0值，该点表示卫星从初始轨道至GEO的整个转移过程完全由电推进完成。另外，点划线位于所有曲线最下方，表示仅采用化学推进进行倾角调整时消耗的燃料较多，也就说明采用电推进调整倾角在燃料消耗方面具有优势。图5中当过渡轨道倾角减小，电推进承担的倾角改变量变小时，整个转移过程耗时减小，这说明电推进段进行轨道平面的调整较为耗时。

可以看出，采用化学推进调整轨道倾角时，轨道转移时间较短，但燃料消耗较多；采用电推进调整轨道倾角时，消耗的燃料较小，但转移时间较长。由于过渡轨道倾角的不同取值，对混合推进转移轨道燃料消耗和转移时间的影响较大，故在本文的搜索网格构建中，加入了轨道倾角变量。

(2)近地点幅角变化对转移轨道设计的影响

这里分析近地点幅角变化对转移轨道设计的影响，在仿真中，选取的初始轨道为近地点高度200 km、远地点高度2 000 km、轨道倾角28.5°、近地点幅角为120°的椭圆轨道，取Isp1=390 s；电推进段Isp2=3 000 s，Tmax=0.2 N。设定过渡轨道近远地点距离与轨道倾角变化影响分析中相同。

化学推进段速度增量ΔVCP随过渡轨道近地点幅角ω和过渡轨道高度的变化如图6所示。图6中的近地点幅角为过渡轨道的近地点幅角，由于初始轨道近地点幅角取为120°，因此不同曲线对应于化学推进段和电推进段对近地点幅角调整的不同贡献。例如，当过渡轨道近地点幅角为120°时，在化学推进段不进行近地点幅角调整，其调整完全由电推进段完成；当过渡轨道近地点幅角为80°时，近地点幅角先由化学推进调整40°，再由电推进调整80°。

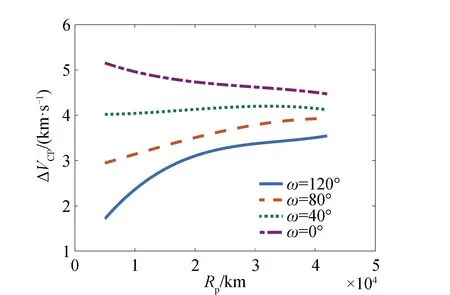
图6 化学推进段速度增量随过渡轨道近地点幅角和 轨道高度的变化曲线Fig.6 The variation of the velocity change in the chemical segment

由图6可知，当轨道高度固定时，过渡轨道的近地点幅角越小，完成轨道转移所需的速度增量越大。这说明，对于近地点幅角的调整，应当由电推进段来承担完成，这样较省燃料。

电推进段转移时间TEP以及速度增量ΔVEP随过渡轨道近地点幅角ω和过渡轨道高度的关系分别如图7和图8所示。

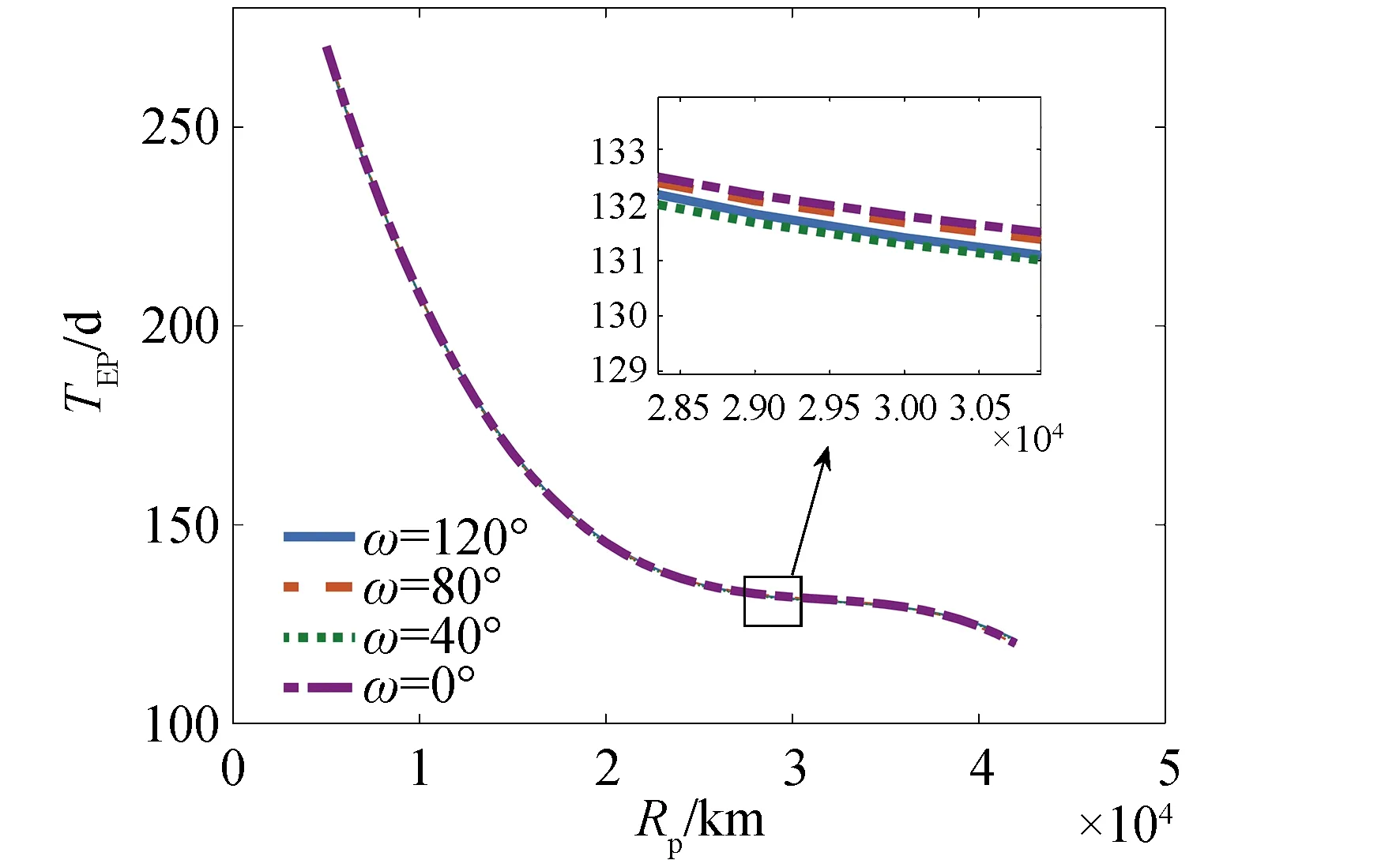
图7 电推进段转移时间随过渡轨道近地点幅角和 轨道高度的变化曲线Fig.7 The variation of transfer time of electric segment

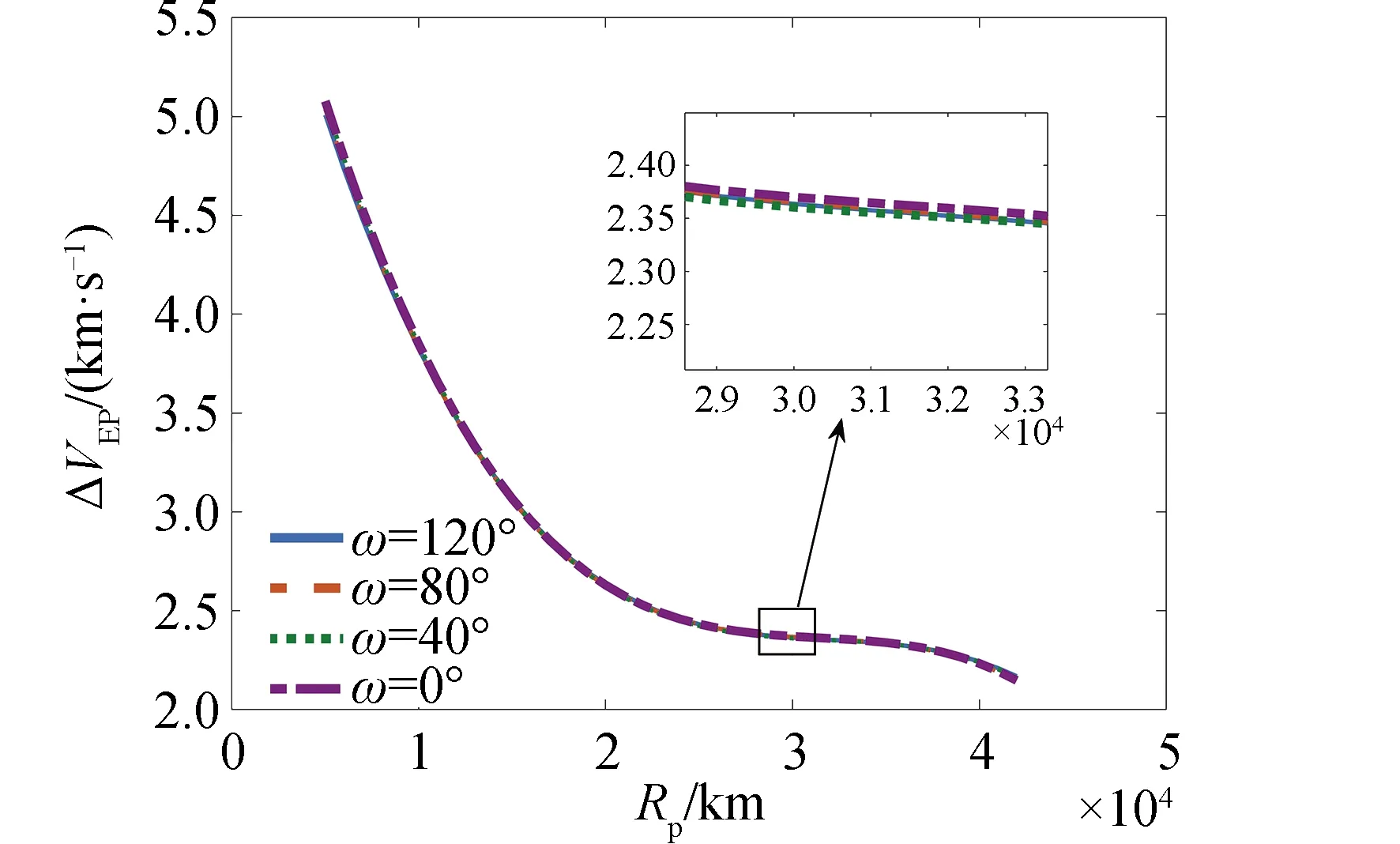
图8 电推进段速度增量随过渡轨道近地点幅角和 轨道高度的变化曲线Fig.8 The variation of velocity change of electric segment

由图7和图8可以看出，对于具有不同近地点幅角的过渡轨道，电推进段轨道转移时间和速度增量的差别不大，说明过渡轨道近地点幅角的变化对电推进转移过程的影响较小。

对图6～图8进行比较可以看出，相比于化学推进，采用电推进进行近地点幅角调整较为有利。因此，本文假定近地点幅角调整全部由电推进完成，故在搜索网格中不设置相应搜索变量。

(3)简化后的搜索网格

最终简化后的搜索网格包含过渡轨道近地点距离、远地点距离和轨道倾角3个维度。以近地点高度Rp为x轴，远地点高度Ra为y轴构建采样网格，其中:

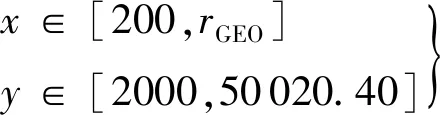
(4)

单位km，且满足x≤y。在此范围内平均取横向格点数11，纵向格点数14，可以得到图2所示的二维网格。在此基础上，增加轨道倾角维度，轨道倾角i的变化范围为：

i∈[0°,9.5°,19°,28.5°]T

(5)

加入了轨道倾角维度之后，搜索网格(见图9)变为三维网格，格点区域覆盖初始轨道至目标轨道之间的整个区域。依照流程(见图3)进行解算，可以得到混合推进轨道在整个搜索域上的优化设计结果。

图9 搜索网格Fig.9 Search grid

3 数值仿真结果

在由搜索网格界定的整个搜索域上，开展混合推进转移轨道优化解算，仿真参数如表1所示。始末质量和转移时间曲面分别如图10和图11所示。

图10中展示了化学-电混合推进转移中始末质量比值在搜索域上的变化规律。可以看到，过渡轨道倾角为28.5°时，对应的曲面位于所有曲面之上，即此时始末质量比值较大。这表示卫星从初始轨道转移至GEO的整个过程中，轨道倾角调整完全由电推进完成，转移的有效载荷最高。相反，过渡轨道倾角为0°的曲面，始终位于所有曲面最下方，说明完全使用化学推进将轨道倾角调整为0°对燃料的消耗最大。值得注意的是，在mGEO/m0比值为0.3～0.4范围内，轨道倾角为9.5°、19°、28.5°三个曲面出现了重合或是相交的部分。结合图11相同转移轨道区域内的转移时间可以看出，在某些情况下，采用化学推进分担部分倾角的调整也是有意义的，能大大减少任务耗时。单就一个曲面而言，可以观察到同一过渡轨道倾角条件下始末质量比值在搜索网格中的变化趋势。可以看出，过渡轨道离初始轨道越远，始末质量比值越小，卫星的质量传送效率越低。

表1 仿真参数

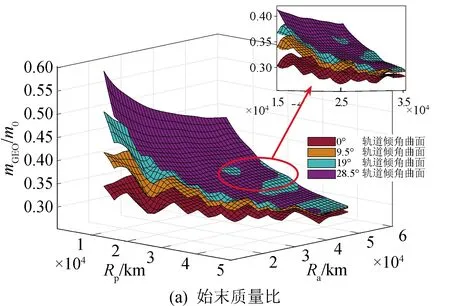
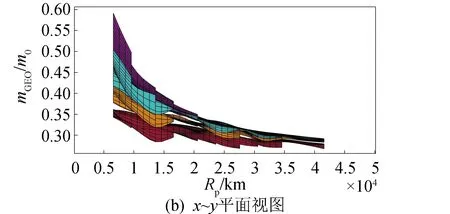
图10 混合推进轨道设计始末质量比值mGEO/m0Fig.10 The beginning-to-end mass ratio mGEO/m0of the hybrid propulsion orbit design

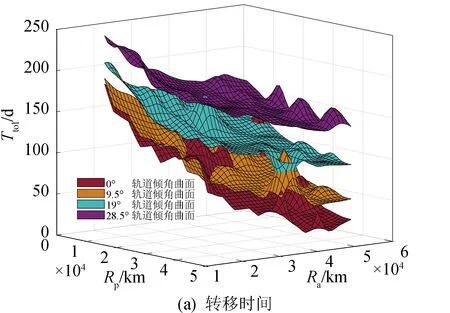
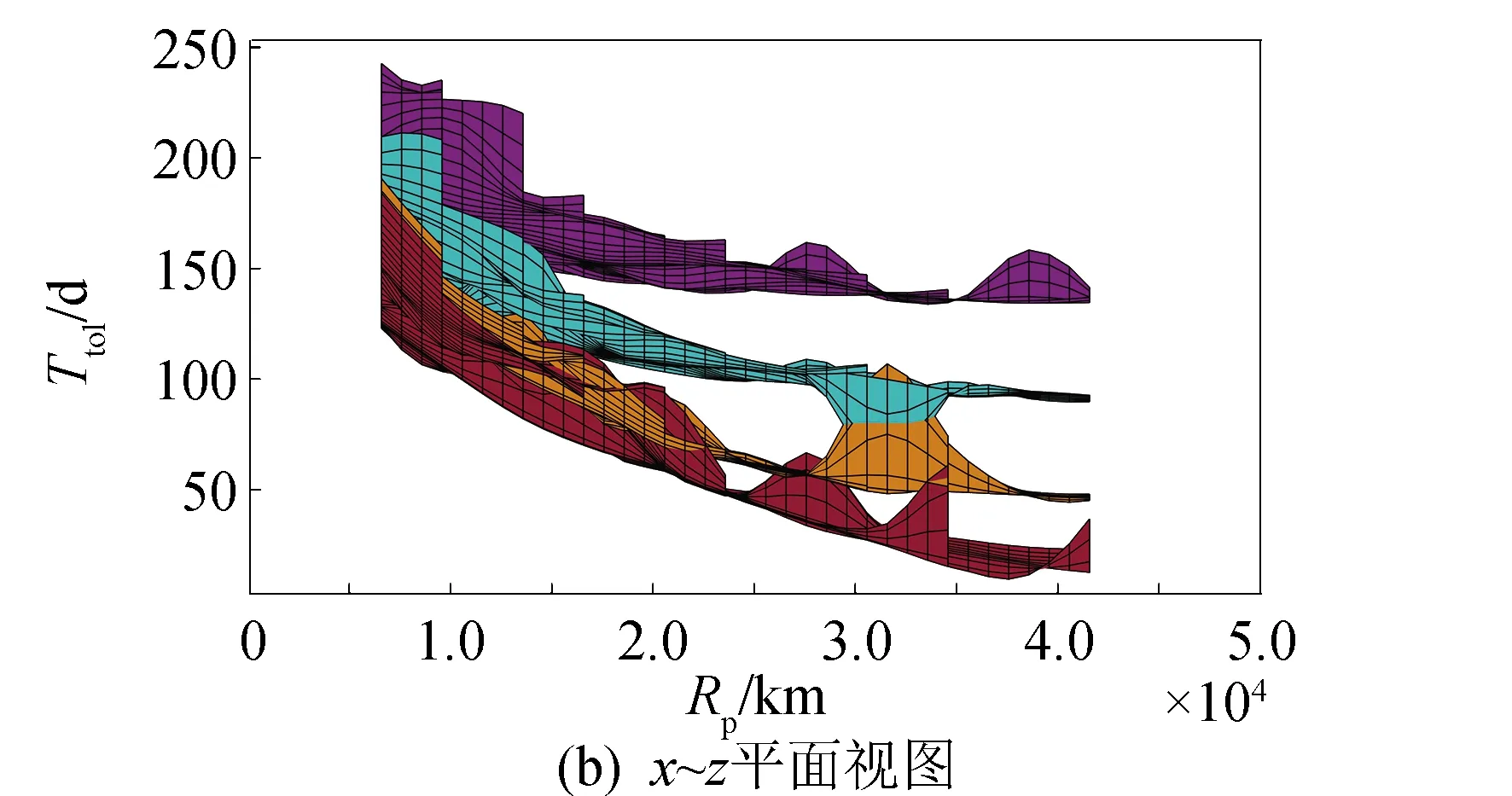
图11 混合推进轨道设计转移时间Fig.11 Transfer time chart of hybrid propulsion trajectory design

图11中展示了混合推进转移时间在整个搜索域内的变化规律。可以看到，过渡轨道倾角为28.5°时，对应的曲面位于所有曲面之上，这说明当轨道倾角完全是由电推进完成时，转移耗时较长。同时也可以看出，若转移完全由化学推进完成，则转移时间最短。值得注意的是，在离初始轨道较近的区域(近地点距离[25 000～40 000]km)范围内，曲面出现了重合或是相交的部分，结合图10中相同区域内的始末质量比，说明可对该区域内的化学推进段做更有效的能耗优化，即在转移时间相同时减少化学推进段对倾角调整的量，达到省燃料的目的。就其中一个曲面可以观察到同一过渡轨道倾角条件下始末质量比值在搜索网格中的变化趋势。值得注意的是，在近地点距离相同时，过渡轨道为大偏心率轨道时的转移时间较小。

图10和图11提供的解算结果，可应用于实际任务轨道的选取。假设任务要求设计一条始末质量比0.55以上、转移时间100～200 d的轨道。由图10可以查出满足始末质量比的过渡轨道范围：倾角9.5°以上，近地点距离10 000 km附近。然后，在图11中相应过渡轨道范围内，选取时间最优解即可。

4 结束语

本文以地球同步轨道卫星化学-电混合推进转移为任务背景，开展轨道优化设计与分析研究，以Ceccherini和Topputo等提出的过渡轨道搜索网格算法模型为基础，增加了过渡轨道倾角维度，以转移始末质量比和转移时间为两个指标，构建起包含化学推进段、过渡轨道段和电推进段的混合推进转移轨道优化和分析方法。借助数值仿真，得出下列结论：

1)本文算法可以提供具有不同燃料消耗和转移时间的混合推进转移解集，相比于全化学推进和全电推进解，拓宽了解空间，方便轨道设计人员根据任务约束灵活选用。

2) 在混合推进轨道的优化中，过渡轨道近地点幅角的取值对电推进段轨道优化结果的影响不大，但对化学推进段的燃料消耗有显著影响。

3)过渡轨道倾角的取值对混合推进转移轨道燃料消耗和转移时间的影响非常显著，应当将其作为搜索网格中的一个维度，开展优化设计。