Walker 星座碰撞检测及碰撞概率分析

吴启星，陈 雨

（1.北京跟踪与通信技术研究所，北京 100094；2.上海微小卫星工程中心，上海 201210）

0 引言

Walker 星座由于其拓扑结构稳定、对地面覆盖均匀等特点，被广泛应用在通信、地面观测及侦察等航天任务中［1-3］，例如GPS、Glonass、北斗等导航卫星，以及铱星、Starlink 等通信卫星系统，均采用了几十乃至上百颗卫星组成的卫星星座。随着星座规模的增大，星座中卫星发生碰撞的风险也越来越大［4］。目前，碰撞检测研究主要针对星座设计时的标准理论构型。文献［5-6］推导得到星座中任意两颗卫星的距离计算公式，通过周期性轮询计算得到整个星座中每两颗卫星的距离情况，从而实现星座中卫星碰撞预估，该方法的缺点是运算量大，且随着星座规模的扩大，运算量会线性增加。文献［7］从概率论的角度出发，认为只要卫星运行到交叉点即有碰撞的可能，通过星座的规模、轨道交点个数，以及每天卫星经过交点的次数，得到该星座发生碰撞的概率。文献［8］根据星座的拓扑构型特点，通过相交轨道面在轨道面交点处的几何关系及相交轨道面卫星间的相位关系，求得星座卫星的最小距离，该方法可准确检测出理论星座构型是否会发生碰撞。

卫星入轨偏差和空间摄动力导致在轨星座构型与理论设计值偏离，需不断进行星座构型维持。因此，星座碰撞检测不仅要考虑理论星座构型下卫星是否会发生碰撞，还要分析当星座中卫星站位发生漂移、实际在轨星座与理论设计星座构型具有偏差时碰撞的可能性。本文设计一种针对Walker 星座的碰撞检测系统模型，能够有效检测设计的理论星座构型是否会发生碰撞，并根据星座实际在轨构型维持策略，在星座构型漂移的情况下给出该星座构型是否具有碰撞风险，计算碰撞概率及安全度系数，实现对星座构型的抗碰撞风险能力评估。

1 Walker 星座构型及维持策略

Walker 星座最早由英国皇家飞行研究中心的沃克提出［9］，其构型用参考码S/P/F表示，其中，S表示星座中卫星的总数目，P表示卫星分布的轨道面数，F为相位因子。Walker 星座中所有卫星轨道高度、倾角、偏心率均相同，且每个轨道面内卫星分布均匀，不同轨道面间卫星的相位（即纬度幅角）保持一定的相对关系，相邻轨道面对应序号卫星的相位差为u=360°⋅F/S，F=0，1，…，P-1。

入轨误差及在轨摄动力的影响导致卫星间的相对相位发生变化，星座构型发散［10］，因此，卫星入轨后需要进行星座构型维持。Walker 星座的构型维持主要为保持星座卫星间的相对位置关系，文献［11］采用了如下基于基准卫星的星座构型维持方法：首先选择基准卫星，以基准卫星为参考建立理论的虚拟参考星座，确定每颗卫星的理论站位；然后根据任务需求，确定相位误差阈值ξu，即星座中每颗卫星的实际位置与理论站位的最大允许相位差，在轨将实际卫星维持在理论站位±ξu范围之内；在相位维持过程中，半长轴的调整具有一定范围约束，需保证半长轴偏差在±ξa之内，如图1 所示。

2 Walker 星座碰撞概率计算

Walker 星座卫星碰撞问题的研究可分为狭义碰撞和广义碰撞［12-13］。

2.1 狭义碰撞

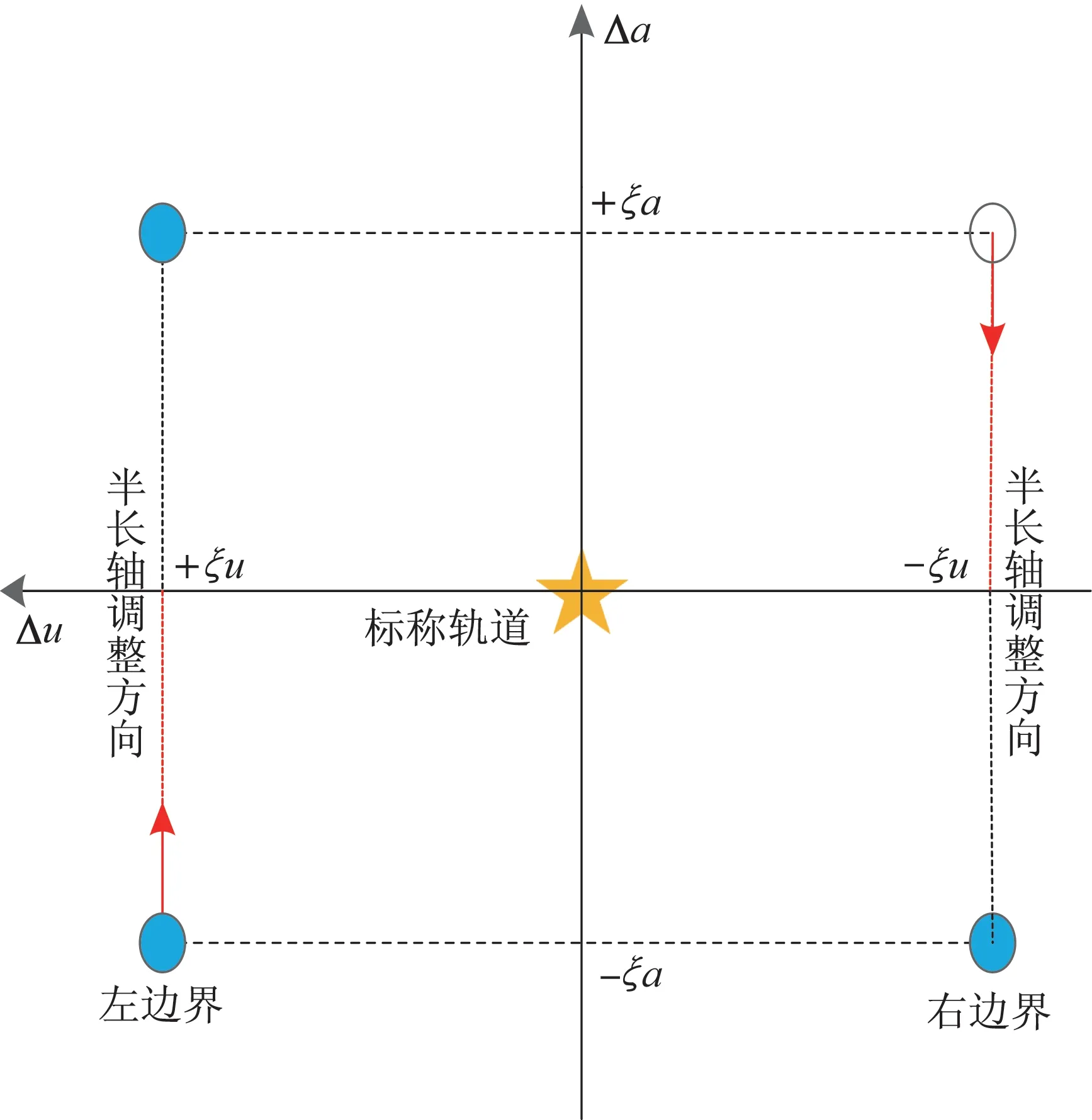
图1 星座构型维持示意图Fig.1 Schematic diagram of constellation configuration maintenance

狭义碰撞将卫星视为一个研究点，只单纯考虑所建立的理论Walker 星座是否会出现某一时刻两颗卫星完全重合的情况。卫星狭义碰撞只发生在轨道交点处，定义相交轨道面上两卫星在过轨道交点时的最小角距为交点卫星角距［7］ξwi：

式中：i=1，2，…，P(P-1)为轨道交点个数；ηi、为轨道交点在两个相交轨道面上的升交角距；同一轨道面相邻相位差Δδ=2πP/S；相交轨道面相对相位Δλk=2πF(k-1)/S，k为相交轨道面序号。

星座发生狭义碰撞的判断依据为

根据式（2），卫星狭义碰撞的条件只与星座构型参数S、P、F以及轨道倾角α有关。若Walker 星座会发生狭义碰撞，则认为此星座的碰撞概率为100%。

2.2 广义碰撞

广义碰撞综合考虑卫星星座实际在轨位置相对于理论站位的偏差范围、实际测定轨误差等，因此，卫星广义碰撞是一种概率碰撞［14］。若在同一时刻星座中的两颗卫星的最小距离小于一定值时，就具有发生碰撞的概率，即会发生广义碰撞。

考虑星座构型维持策略，在轨道半长轴相同的情况下，若两颗卫星发生广义碰撞，必然有某一时刻两颗卫星在轨道交点处存在相位阈值区域相交的情况。假设以卫星i和卫星j的相位阈值区域均进入两轨道交点为开始，到卫星i或卫星j（任意一个）相位阈值区域离开两轨道面交点为结束，此段时间内两星的状态称为相位相交，相交时间段内每颗卫星划过的相位值Δu相同，称为相交相位，如图2 所示。此时，卫星i到达两轨道交点位置，卫星j即将到达轨道交点，两星间相位差为ξw。

图2 两星相位相交示意图Fig.2 Schematic diagram of the phase intersection of two satellites

求得两星相交相位值为

当两星的相交相位为Δu时，不考虑卫星外形尺寸，且将实际卫星相对于理论站位动态运行的区域看作矩形区域，按照10 m 为单位对该区域进行单元格划分（设单个卫星体积直径为5 m），视两颗星同一时刻均落到同一个单元格的情况为两颗星发生碰撞，卫星i实际落入相位相交区域的概率为

在卫星i落入该区域的条件下，卫星j与其碰撞的概率为

另外，考虑两颗卫星半长轴相同的概率为

综上，两卫星碰撞的概率为

式中：R为轨道半长轴；R、ξa单位为km；Δu、ξu单位为弧度。

3 构型维持条件下Walker 星座碰撞检测

3.1 构型维持条件下碰撞检测方法

当卫星星座在不存在狭义碰撞时，仍需保证星座建立后在正常的构型维持策略下卫星发生碰撞的概率尽可能小，即所设计Walker 星座中，不存在两颗卫星在某一时刻出现相位相交的情况，如图3 所示。当两颗卫星的相位阈值区间前后到达两轨道交点的时间差大于图3 所示情况时，两颗星必不相撞，即发生碰撞的概率为0。

图3 相位相交的临界状态示意图Fig.3 Schematic diagram of the critical state of phase intersection

在该临界状态下，两颗星到轨道交点的角距均为ξu，此时为两颗星距离最近的时刻，求得该情况两星的角距为

式中：Ω为Ai、Aj所对应的球面角；r为根据实际星座构型维持相位阈值得到的非碰撞条件下所需的理论最小卫星角距，即临界角距，若星座中最小卫星角距小于此值，则不会发生碰撞。

3.2 星座构型防碰撞性分析

通过检测确定的不会发生广义碰撞的Walker 星座，是建立在构型维持策略正常进行，且构型维持结果符合控制要求基础上的。若考虑构型维持也有产生误差的可能，通过检测不会发生在轨碰撞的Walker 星座也有发生碰撞的风险，如图4 所示。当出现相位维持正偏差时，即图4（a）所示情况，此时出现的相位误差会增大两星的最小距离，不会产生碰撞风险；当出现相位维持负偏差时，即图4（b）所示情况，此时出现的相位误差会减小两星的最小距离，则会引起碰撞风险。

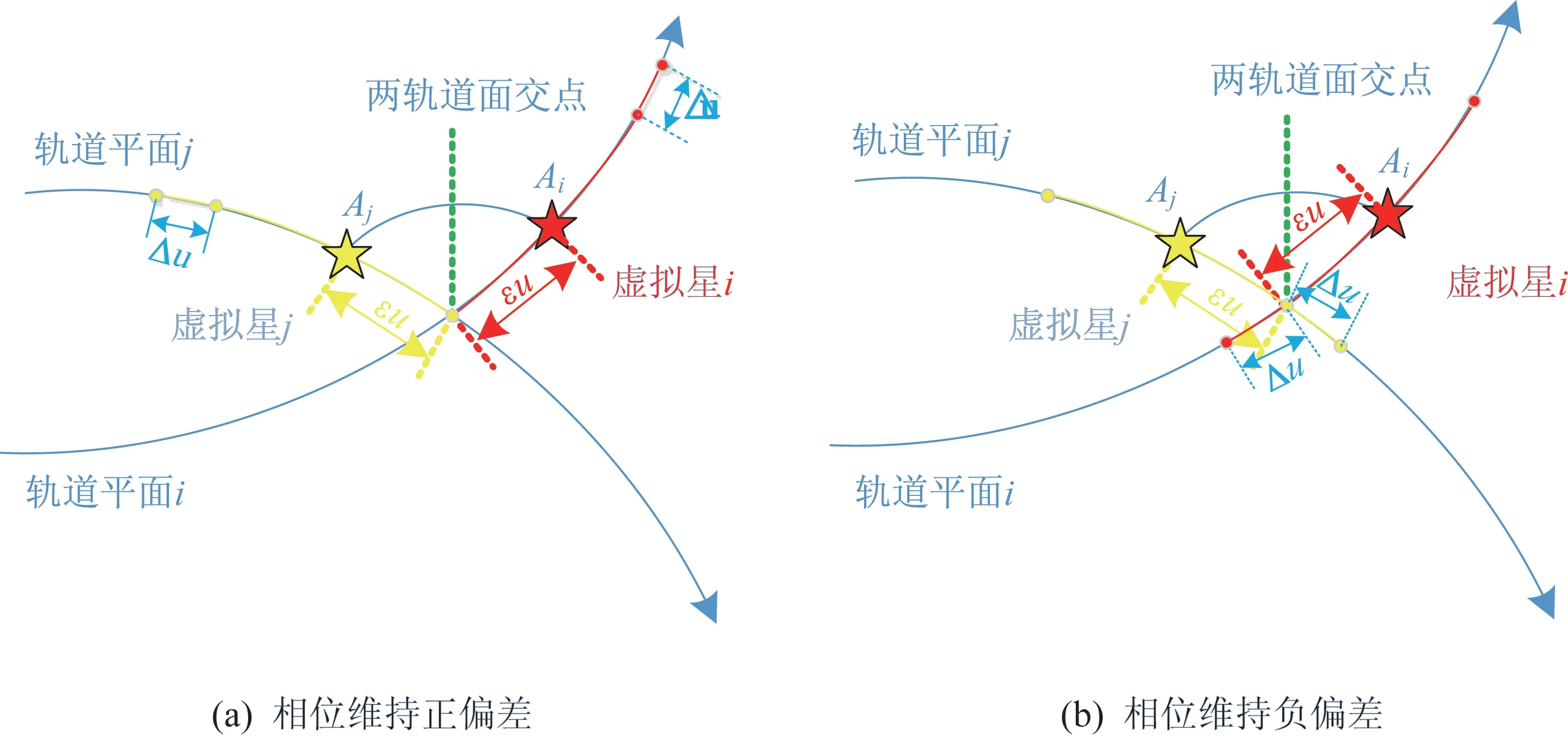
图4 相位维持偏差示意图Fig.4 Schematic diagram of phase maintenance deviation

本节提出了一种表征Walker 星座构型防碰撞性能的安全度系数kr，其表达式如下：

式中：r'为星座最小卫星角距；r为对应的临界角距，

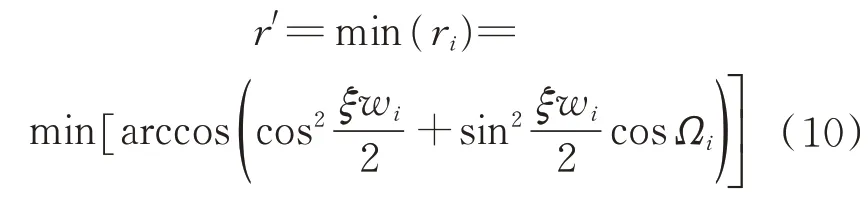
当星座构型通过检测不会发生广义碰撞时，安全度系数kr越大，抗风险能力越好，发生碰撞的可能性越低［15］。在星座其他性能一致的情况下，选取抗风性系数较大的星座构型更有利于星座的稳定性。

4 Walker 星座防碰撞检测系统模型及仿真分析

4.1 Walker 星座防碰撞检测模型

根据Walker 星座构型维持及碰撞特性分析，建立Walker 星座防碰撞检测模型。对于给定的Walker 星座构型及星座在轨控制相位阈值，检测是否存在碰撞风险，输出碰撞概率；对于不存在碰撞风险的Walker 星座，输出安全度系数。该系统数据流图如图5 所示。

图5 星座碰撞检测数据流图Fig.5 Flow chart of constellation collision detection data

具体Walker 星座防碰撞检测模型流程如图6 所示，该Walker 星座碰撞检测系统可检测Walker 星座是否会发生碰撞，并定量给出碰撞概率。对于不存在碰撞风险的Walker 星座构型，给出其安全度系数，用于星座构型的最优选择。

图6 Walker 星座碰撞检测模型Fig 6 Model of Walker constellation collision detection

4.2 仿真算例

本节利用Walker 星座防碰撞检测模型分析星座在轨构型维持条件下的防碰撞性能，实现星座构型择优。以72 颗卫星组成的Walker 星座为例，卫星轨道高度为600 km，倾角60°，偏心率为0，设计星座在轨构型维持相位阈值为±4°，半长轴维持阈值为±50 m。

1）分别仿真轨道面个数为6 和9 时，在不同相位因子条件下，星座的防碰撞特性见表1 和表2。

根据表1 和表2 的仿真结果，由72 颗卫星组成的Walker 星座，当轨道面个数为6：在相位因子F为0、2 和4 时，星座最小卫星角距为0，会发生狭义碰撞；在相位因子为1、3 和5 时，星座会发生广义碰撞，卫星交汇时的碰撞概率分别为1.472×10-9、5.614×10-9和2.653×10-9。当轨道面个数为9：相位因子选取0～8 时，星座均不会发生狭义碰撞；当相位因子选择0、1、2、4、5 和8 时，会发生广义碰撞，碰撞概率分别为5.412×10-10、2.382×10-9、7.503×10-10、4.652×10-9、5.899×10-10和5.899×10-10；相位因子为3、6 或者7 时，星座既不会发生狭义碰撞，也不会发生广义碰撞，此时，计算3种构型的安全度系数分别为0.026、0.106以及0.417，安全度系数越大，则碰撞风险越低，因此，若单考虑碰撞问题，则选取（72，9，7）Walker星座构型可靠性最高。

2）Walker 星座构型选择（72，9，7），仿真星座构型中最小卫星角距和安全度系数随倾角的变化情况如图7 和图8 所示。仿真结果表明，在星座构型一定的情况下，最小卫星间距随倾角变化而变化，倾角在60°附近，最小卫星间距达到较大值。在图8 中，轨道倾角为［38，58］、［64，71］、［75，85］、［87，89］时，安全度系数小于0，表明此星座会发生广义碰撞，当轨道倾角为86°时，安全度系数为1.4，达到最高值，此时星座的防碰撞性能最优。

3）针对目前组网的通信星座卫星数量较多，对480 颗卫星、30 个轨道面组成的大型Walker 星座，仿真星座构型中最小卫星角距和临界角距随相位因子的变化情况（相位阈值为3°，轨道倾角89°）如图9 所示。仿真结果表明，在卫星总数、轨道面个数确定的情况下，不同相位因子的星座碰撞特性不相同。

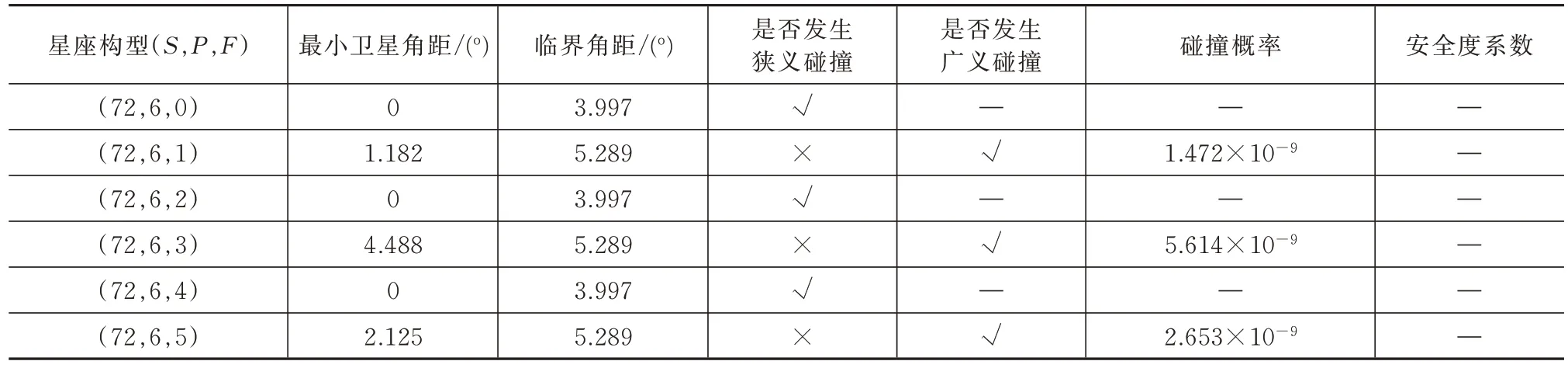
表1 星座防碰撞特性（P=6）Tab.1 Constellation anti-collision characteristics（P=6）

表2 星座防碰撞特性（P=9）Tab.2 Constellation anti-collision characteristics（P=9）

图7 最小卫星角距随卫星倾角变化情况Fig.7 Changes of the minimum angular distance with the satellite inclination

图8 安全度系数随卫星倾角变化情况Fig.8 Changes of the safety factor with the satellite inclination

在图9 中，最小卫星角距为0 的会发生侠义碰撞；最小角距不为0 且小于临界角距的会发生广义碰撞；最小卫星角距大于临界角距的既不会发生侠义碰撞也不会发生广义碰撞，对应相位因子为6、16、18、22。

图9 最小卫星角距/临界角距随星座相位因子变化情况Fig.9 Changes of the minimum/critical angular distance with the constellation phase factor

5 结束语

本文基于Walker 星座狭义碰撞的研究成果，根据卫星星座的在轨维持策略，研究了在构型维持阈值下的Walker 星座广义碰撞的检测模型，对于可能发生广义碰撞的Walker 星座，给出了星座碰撞概率的计算方法，对于正常情况下不会发生广义碰撞的Walker 星座，提出了表征星座防碰撞安全性等级的非碰撞安全度系数。案例仿真分析表明，本文提出的Walker 星座碰撞检测模型可以准确计算星座防碰撞风险能力，解决了在同等条件下的星座构型择优问题，具有很好的工程应用价值。