面向卡塞格伦伞状天线的主副面同步展开机构设计及分析
韩晓童,王晓凯,邢永涛,张树新
(1.西安电子科技大学电子装备结构设计教育部重点实验室,陕西 西安 710071;2.上海宇航系统工程研究所,上海 201109)
0 引言
目前发展较为成熟的星载可展开天线,例如固面式[1]、充气式[2]、构架式[3-4]及周边桁架式[5-7]等,都难以同时满足高收纳比、高精度的要求。而伞状可展开天线[8-11]在收纳比、面密度、展开性能以及在轨热环境下的形面保持等方面,具有突出的优势,受到了众多国际宇航研究机构的高度关注和广泛研究。
伞状天线又称为支撑肋可展开天线,是指柔性反射面由肋支撑,收拢时支撑肋收拢,在轨后支撑肋展开带动柔性反射面展开到工作状态的可展开式天线。伞状天线的分类主要根据支撑肋的不同进行分类,可分为缠绕肋天线[12]、径向刚性肋天线[13]和可收拢肋[14]天线。缠绕肋天线结构简单,收纳比高,可以研制出超过30 m 的单一模块天线,但其刚度、抗振性、反射面精度都比较差。径向肋天线最早由美国TRW 公司研制,具有高精度及高刚度,可收拢肋天线收拢时不仅各条肋可以进行收拢,每条肋也可进行自身的收拢。
美国喷气推进实验室(JPL)Chahat 等[15-16]公开了一种小型伞状可展开天线的原理样机的展开过程,该伞状天线在气体推动的作用下天线开始进行展开,天线主反射面和副反射面主要通过弹簧进行展开,每一根天线肋通过各自的恒力弹簧和弹簧片联合作用完成天线尖肋的展开。该伞状可展开天线具有三次较大冲击,分别是气体推动瞬间、副面完全展开瞬间和天线肋完全展开瞬间,且天线展开同步性较差。
之后Chahat 等[17-18]对展开机构进行改进,将气体推进的展开方式改为以丝杠螺母机构作为推进机构,增加了轮毂底座展开时的稳定性,但是依然存在天线肋展开时同步性较差、存在两次较大冲击等问题。我国发射的“鹊桥”[19-21]伞状可展开天线,采用缓释弹簧分布式驱动展开技术实现天线在轨展开功能,机构内部分为两个模块,分别为动力模块和传动模块。缓释弹簧分布式驱动展开技术采用动力多点布局,展开过程中保证所有动力源输出动力和速度的一致性,最大限度地降低了由于单点失效带来的可靠性下降问题和天线展开速度控制问题。但对于长焦距卡塞格伦式天线,该展开机构收拢后结构不够紧凑。
展开过程是可展天线最容易出现故障的环节之一,天线展开过程不稳定,容易产生过大的冲击,造成展开过程的失败。因此,在设计阶段,对天线的展开过程仿真来预测展开性能是十分重要的。针对长焦距卡塞格伦式天线结构特征,本文提出了一种基于曲柄滑块与绳索机构相结合的伞状天线展开机构,对主副面展开过程进行速度规划和仿真分析,确定最优速度规划,验证展开过程满足稳定的要求。
1 伞状天线展开机构总体设计
1.1 设计依据
星载可展开天线机构设计的目的是使其具有收拢体积小、展开过程稳定等特点。针对长焦距卡塞格伦天线的结构特点,为满足收拢后结构更加紧凑,展开时需要进行副面和主面的两次展开。对于现有副面需要展开的卡塞格伦式伞状可展开天线,为副面与主面每条肋各自进行展开,展开方式为弹簧、扭簧驱动展开,展开过程冲击较大。当要求主面与副面同时展开时,只需要一个驱动,因此,可通过副面的展开来驱动主面的展开。而副面展开时为直线运动,主面展开时为旋转运动,因此,需实现主面展开时直线运动到旋转运动的转换。当曲柄滑块机构以滑块为主动件时,能够实现直线运动到旋转运动的转换。
在类似曲柄滑块机构的作用下,主面单根天线肋的展开过程运动简图如图1 所示。图中:O点表示天线肋转动铰链中心;A点表示连杆与天线肋铰接中心;B点表示连杆与滑块铰接中心;C点表示天线肋顶点。天线展开时,副反射面需向上运动,而滑块需向下移动完成主面的展开,因此,可通过绳索和定滑轮的作用,实现天线展开时副反射面对滑块的反向拉动。

图1 天线单根肋展开过程运动简图Fig.1 Schematic diagram of the antenna single rib deployment process
1.2 展开机构设计
天线完全展开态剖面示意图如图2 所示。天线展开机构主要由底座、天线肋、连杆、滑块、绳索机构和副反射面组成,其中绳索机构包含绳索与定滑轮。天线收拢时,副面高度近似于天线肋高度。天线在展开时,主动件为副反射面。天线的副反射面上升时,通过绳索机构的作用,绳索拉动滑块向下运动,再通过连杆传递力的作用,使天线肋进行展开。副面到达固定位置后,天线完全展开,实现了天线副反射面与主反射面的同步展开。天线副反射面完全展开后,绳索具有一定的弹性,能够实现天线形态的保持。
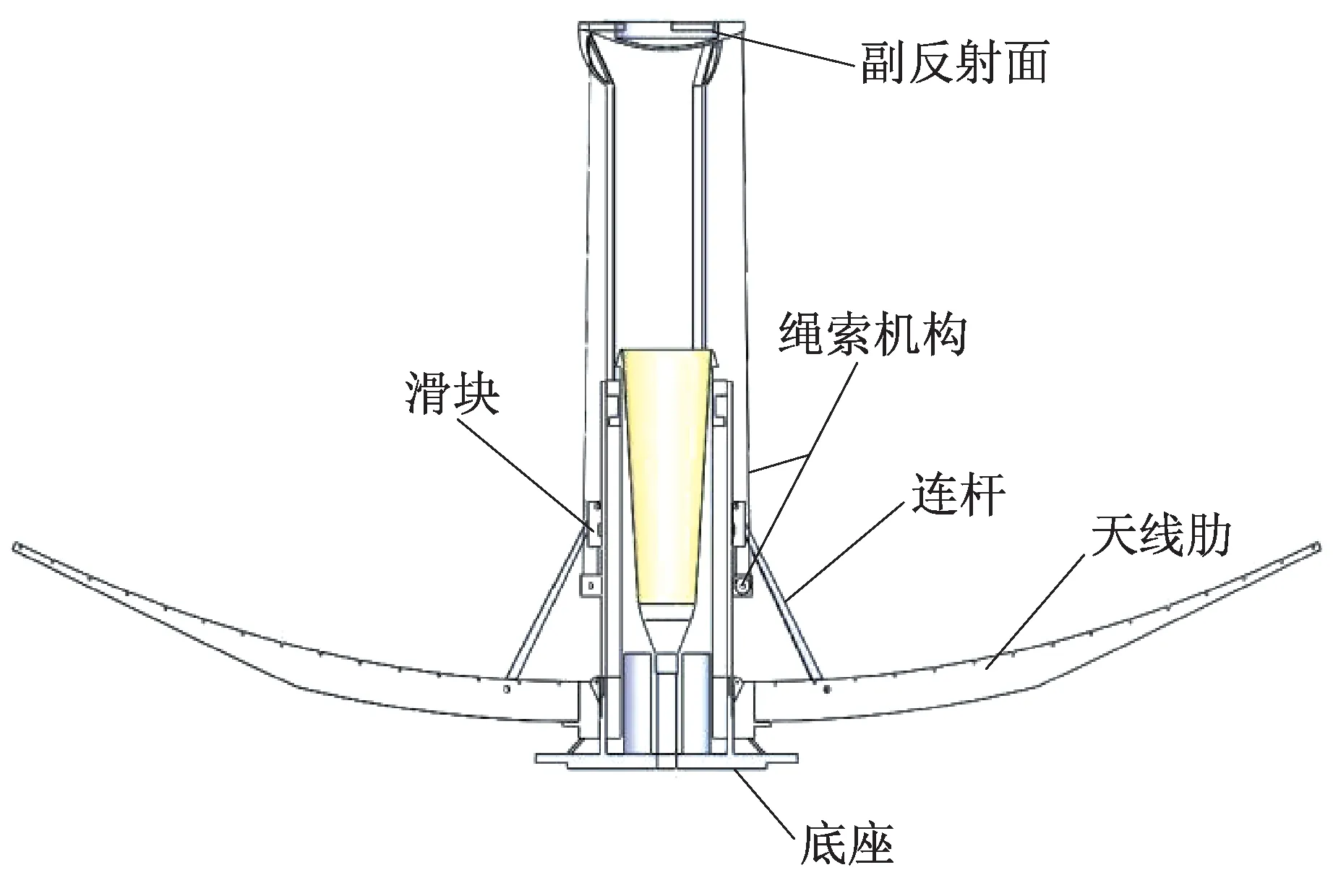
图2 天线完全展开态剖面示意图Fig.2 Profile diagram of the fully deployed antenna
本文设计的展开机构应用于卡塞格伦双反射面天线,得到天线完全展开时的整体三维实体模型图,如图3 所示。

图3 伞状天线完全展开态三维实体模型图Fig.3 Three-dimensional entity model of the fully deployed umbrella-type antenna
2 伞状天线展开过程分析
2.1 位置分析
将天线单根肋的展开过程运动简图在坐标系中表示,天线展开机构各部件间的位置及角度关系如图4 所示。图中:O、A、B、C代表的点与图3 相同;θ表示天线肋展开时角度;β表示AC连接线与OA延长线夹角;r表示滑块运动在y方向位置。

图4 坐标系中单根肋展开机构运动简图Fig.4 Kinematic sketch of the single rib deployment mechanism in the coordinate system
B、C点的坐标为

式中:xB为B点在x方向的坐标;yB为B点在y方向的坐标;xC为C点x方向的坐标;yC为C点 在y方向的坐标;lOA为O、A点连接线的长度;lAC为A、C点连接线的长度;β为定值;滑块的运动为y方向上下滑动;改变θ,可得到天线肋顶点的运动轨迹。
2.2 展开速度和加速度分析
展开角度θ与滑块位置r的关系方程为

式中:lAB为A、B点连接线的长度。
以滑块位置r为自变量,建立展开角度θ与滑块位置r的关系为

式(4)两端同时对时间t求一阶导,得到展开角速度与滑块速度之间的变换方程为

式(5)对时间t求一次导,得到展开角加速度与滑块加速度之间的变换方程为

滑块位置r随时间t的变化函数为
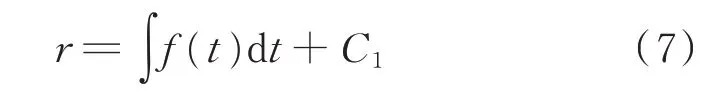
式中:f(t)为规划滑块运动的速度的变化规律;C1为保证函数连续性而待确定的量。
这样就从机构运动学的角度,得出了天线在整个展开过程中天线展开角度θ、角速度、角加速度与每一个展开时刻t的对应关系。
2.3 滑块速度规划
天线展开过程是否平稳,直接影响展开过程是否会出现大的振动。因此,有必要对伞状天线的展开过程进行运动规划。为了使副面展开时更加平稳,对比滑块在不同速度下天线肋展开时的稳定性,为减小最大角速度和角加速度,对滑块分别进行匀速[22]、匀加速匀减速[23]、三次多项式[24]、五次多项式[25]和正弦函数[26]的速度规划。
滑块以匀加速匀减速运动时,滑块速度规划满足如下函数
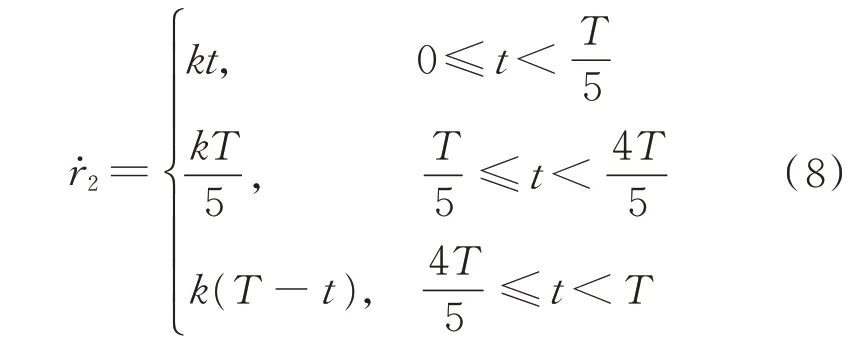
滑块运动满足关系式

式中:H为滑块运动的总行程。
滑块速度以三次多项式变化时,三次多项式函数定义为

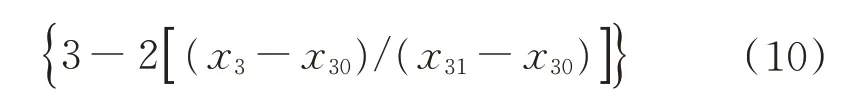
式中:x3为自变量;x30为阶跃函数起点自变量的值;h30为阶跃起点处函数值;x31为阶跃函数终点自变量值;h31为阶跃终点函数值。
滑块以三次多项式规划运动时满足函数
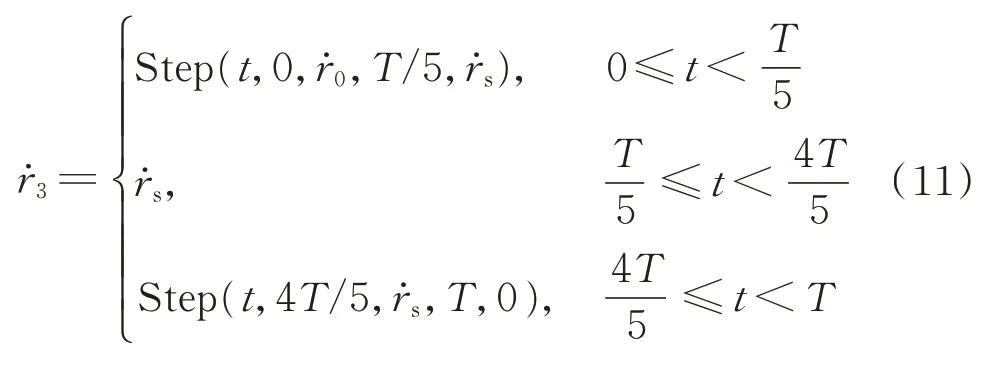
滑块运动总行程H满足关系式
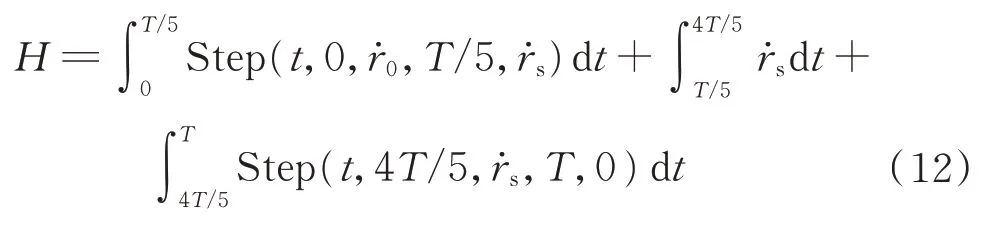
滑块以五次多项式运动时,五次多项式函数定义为
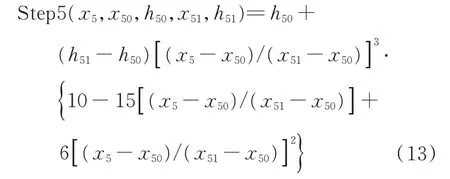
式中:x5为自变量;x50为阶跃函数起点自变量的值;h50为阶跃起点处函数值;x51为阶跃函数终点自变量值;h51为阶跃终点函数值。
滑块以五次多项式规划运动时函数满足

滑块运动总行程H满足关系式

滑块速度以正弦函数规划运动时满足函数
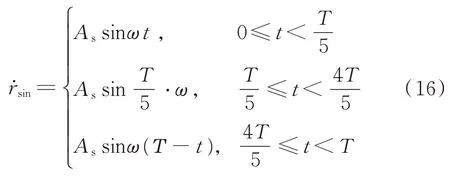
滑块运动总行程H满足关系式
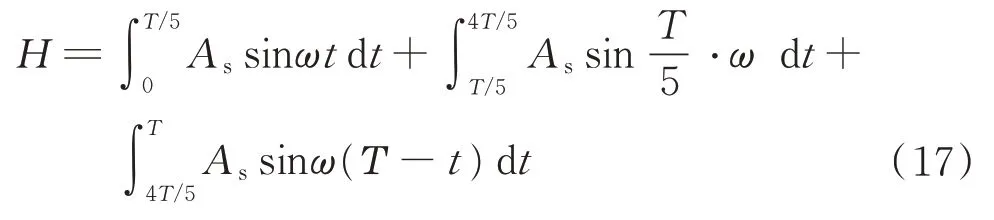
滑块速度分别按照匀速、匀加速匀减速、三次多项式、五次多项式和正弦函数进行速度规划时滑块的速度变化曲线,分别如图5(a)~图5(e)所示。

图5 滑块速度变化曲线Fig.5 Slider velocity curves
3 实例仿真
3.1 运动学仿真
伞状可展开天线为完全对称结构,每一根肋的展开机构完全相同,选取一根肋对其进行运动仿真研究。已知lOA=34.33 mm,lAB=69.38 mm;r0为滑块在初始状态时y方向坐标,值为101.68;设滑块从完全收拢态到完全展开态总行程H为43.7 mm,为初速度,值为0,展开总用时T为10 s。
滑块以匀速运动时滑块行程的变化满足关系式

式中:r1为滑块以匀速运动时行程的变化;为滑块以匀速运动时速度大小;C0为保证函数连续性而待确定的量。代入数据可得,C0=r0=101.67。将式(18)代入到式(5)和式(6),可得到天线肋展开时角速度和角加速度随时间t的变化规律。
滑块以匀加速-匀速-匀减速运动时,代入数据到式(8)和式(9),可得。对式(8)积分可得每个时间段内滑块行程的变化为

式中:r2为滑块以匀加速-匀速-匀减速运动时滑块行程的变化;C1、C2、C3为保证函数连续性而待确定的量,代入数据可得C1=101.67,C2=106.96,C3=194.35。将式(19)代入到式(5)和式(6),可得匀加速匀减速速度规划下,天线肋展开时角速度和角加速度随时间t的变化规律。
滑块以三次多项式的速度规划运动时,代入数据到式(10)~式(12),可得=-43.7/8。对式(11)积分可得每个时间段内滑块行程的变化为
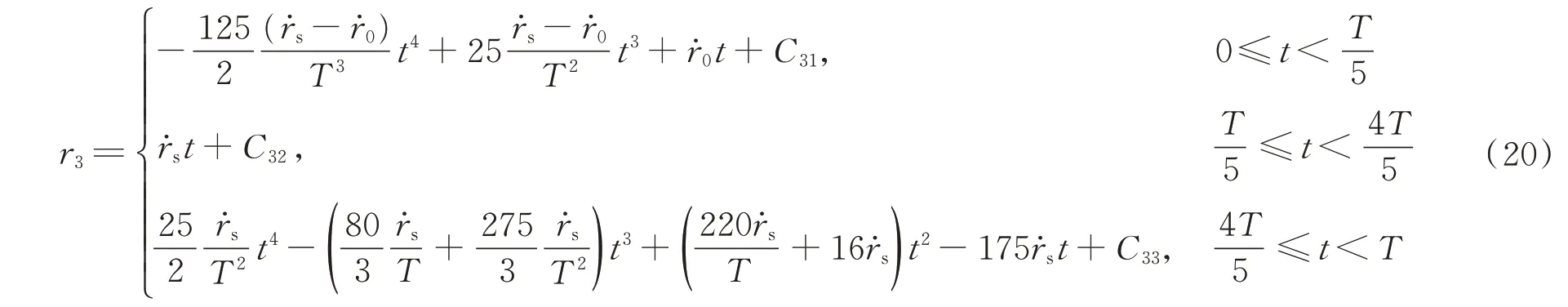
式中:r3为滑块以三次多项式的速度规划运动时滑块行程的变化;C31、C32、C33为保证函数连续性而待确定的量,代入数据可得C31=101.67,C32=107.21,C33=-1 990.50。将式(20)代入到式(5)和式(6),可得三次多项式速度规划下,天线肋展开时角速度和角加速度随时间t的变化规律。
滑块以五次多项式的速度规划运动时,代入数据到式(13)~式(15),可得。对式(14)积分可得每个时间段内滑块行程的变化为
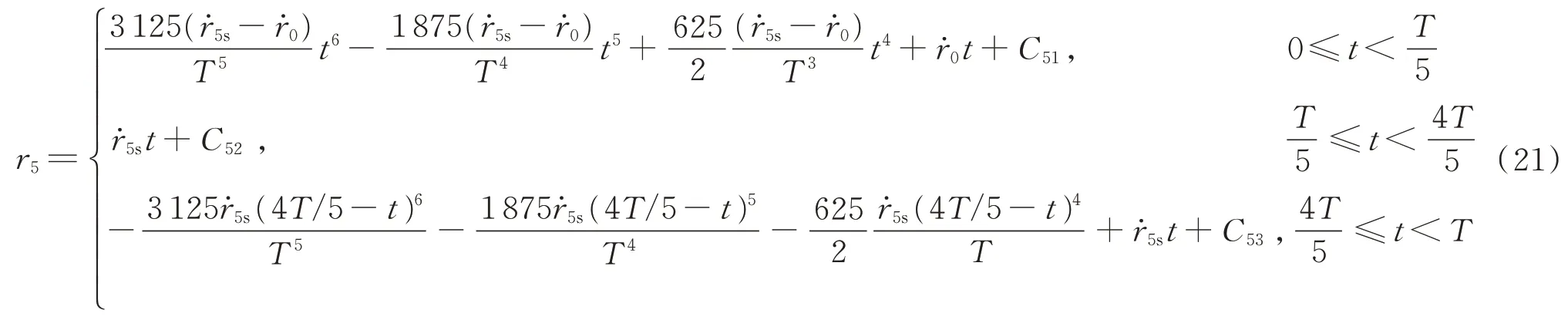
式中:r5为滑块以五次多项式的速度规划运动时滑块行程的变化;C51、C52、C53为保证 函数连续性而待确定的量,代入数据可得C51=101.67,C52=107.13,C53=85 409.50。
将式(21)代入到式(5)和式(6),可得五次多项式速度规划下,天线肋展开时角速度和角加速度随时间t的变化规律。
滑块以正弦函数的速度规划运动时,代入数据到式(16)~式(17),可得。对式(16)积分可得每个时间段内滑块行程的变化为
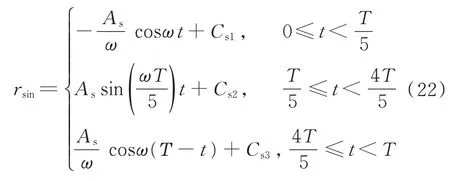
式中:rsin为滑块以正弦函数的速度规划运动时滑块行程的变化;Cs1、Cs2、Cs3为保证函数连续性而待确定的量,代入数据可得Cs1=95.16,Cs2=105.39,Cs3=64.48。将式(22)代入到式(5)和式(6),可得正弦函数速度规划下,天线肋展开时角速度和角加速度随时间t的变化规律。
滑块速度分别按照匀速(uniform velocity)、匀加速匀减速(uniform acceleration)、三次多项式(cubic polynomial)、五次多项式(quantic polynimial)和正弦函数(sine funcation)进行速度规划时,得到的滑块速度变化曲线如图6(a)所示,滑块加速度变化曲线如图6(b)所示。
在不同速度规划下进行天线肋的展开过程仿真,为验证仿真可靠性,对天线肋的展开过程分别进行Matlab 数值仿真与ADAMS 软件仿真。ADAMS 软件仿真时,将简化的三维实体模型导入到多体系统动力学分析软件ADAMS 中,然后根据模型的材料和约束特性设置相应的材料属性和约束。在驱动滑块上设置驱动函数,驱动滑块将按照驱动函数进行运动,从而进行运动学仿真。
设软件仿真设时间为10 s,步数为200。两种方法得到天线展开时肋顶点的运动轨迹如图7 所示。滑块分别在匀速运动速度规划、匀加速匀减速速度规划、三次多项式速度规划、五次多项式速度规划和正弦函数速度规划下运动时,天线肋展开时质心角速度变化曲线,分别如图8(a)~图8(e)所示,天线肋质心角加速度变化曲线分别如图9(a)~图9(e)所示。

图6 不同速度规划下滑块运动变化曲线Fig.6 Velocity curves of the sliding block in different velocity planning
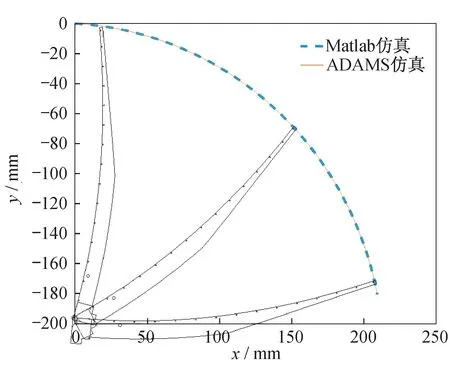
图7 天线展开时肋顶点的运动轨迹Fig.7 Movement track of the rib vertex of the antenna when it is deployed
滑块采用不同的速度规划进行天线肋的展开时,由图6、图8 和图9 可以看出,当天线采用五次多项式速度规划进行展开时,副面与天线肋展开过程的速度加速度连续性更好,为满足天线主副面展开过程的平稳性,滑块采用五次多项式的速度规划进行天线肋的展开较为合理。

图9 天线肋角加速度变化曲线Fig.9 Angular acceleration curves of the antenna when it is deployed
3.2 接触力仿真
在天线肋和底座之间添加接触力,ADAMS 中接触力[27-28]的法向力计算方法有补偿法和基于碰撞函数的接触算法两种。补偿法需要确定两个系数——惩罚系数和补偿系数,而这些数据一般需要通过实验测得。本文选用基于碰撞函数的三维接触力(IMPACT 型接触力)。
IMPACT 函数的格式为
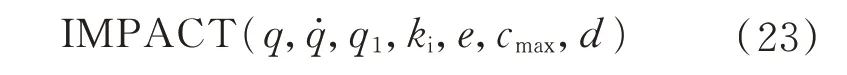
式中:q为距离变量,用来定义两个点之间的距离;为q对时间的导数,通常是速度;q1为IMPACT 的阀值,当q>q1时,IMPACT 为0,当q≤q1时,IMPACT不为0;ki为刚度系数;e为力指数;cmax为最大阻尼系数;d为阻尼达到最大值时的切入量。
对于铝材与铝材接触,以上参数值的选取见表1。

表1 IMPACT 接触力参数Tab.1 IMPACT contact force parameters
IMPACT 函数的返回值如下:
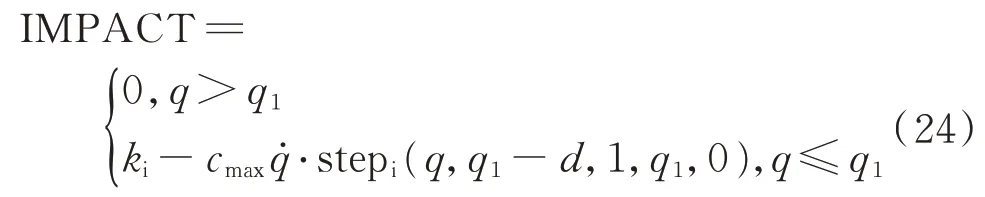
式中:stepi为ADAMS 中的阶跃函数;ki(q1-q)e为弹性力;⋅stepi(q,q1-d,1,q1,0)为阻尼力。当e=1,cmax=0 时,IMPACT 函数相当于只产生压缩的线性弹簧。
滑块采用以上5 种速度规划进行展开时,相应的接触力变化曲线如图10 所示。滑块运动到9.5 s时,天线肋在不同速度规划下开始相继和底座相接触,接触力变化满足式(24),由于天线行程一定,天线完全展开后的预紧力约为104 N。

图10 接触力变化曲线Fig.10 Contact force curves
滑块采用不同的速度规划进行天线肋的展开,由图10 可以看出,当天线采用五次多项式速度规划进行展开时,天线肋与底座的接触力变化曲线更加平稳,天线展开过程中冲击最小。综合天线肋展开过程中角速度与角加速度变化曲线,滑块采用五次多项式速度规划为最优速度规划。
4 结束语
本文针对长焦距卡塞格伦式双反射面伞状天线,提出了一种曲柄滑块机构与绳索机构相结合的展开机构,实现了主副面的同步展开,天线收拢后结构紧凑。建立了天线展开过程的运动分析模型,通过实例仿真,对比不同的速度规划下天线展开时副面的速度、加速度变化与天线肋的角速度、角加速度、接触力变化,确定在五次多项式速度规划下展开最为合理。

