基于输入整形方法的2 自由度机械臂运行过程振动抑制

张美艳，邹怀武，王和庆，唐国安

（1.复旦大学 航空航天系，上海 200433；2.上海宇航系统工程研究所，上海 201109）

0 引言

机械臂因其灵活可变的运行形态，对于不同任务具有较强的适应能力，在空间技术方面有着广泛的用途，如内置载荷释放、目标星捕获、空间垃圾回收、资源补给、舱外设备安装和维修、空间站交会对接、支持航天员出舱活动等［1-4］。

由于空间应用领域对部件设备的自重指标都有较大的限制，面向在轨应用的机械臂强度和刚度设计裕度相对较低。然而，空间机械臂经常需要转运质量、惯量较大的对象，小至航天器的有效载荷，大至卫星整体或舱体整器。机械臂的刚度低，而转运对象的质量大，两者结合后组合体的转运应视为动力学过程，强度校核也应计入动态载荷。

动态载荷一部分是由变速运动加速度引起的，通过优化机械臂的行程（轨迹）可以克服或削弱，是机器人或机械臂动力学与控制研究的主要内容之一。

这方面的研究是从机械臂角度入手，较少考虑转运对象的弹性特征，因此，不同的对象有可能规划出相同的行程。动态载荷的另一部分是因为弹性振动引起的，与被转运结构的惯性和弹性特性有关，相同行程的转运过程也会产生不同的振动响应。这部分振动可考虑用输入整形方法进行抑制。输入整形方法是一种根据结构振动特性（包括固有频率和模态阻尼）对外力函数进行整形，使得经过整形的外力函数激励结构所产生的动态响应比原外力函数激励下的响应更小［5-7］。

从Laplace 变换的角度观察输入形方法，其基本原理就是整形后外力函数所包含的零点恰好就是结构的激励-响应传递函数的极点，理论上结构在这样的外力函数作用下不会激起自由振动响应的。因此，当外力激励停止后结构就不再有残余振动。输入整形方法在机械臂以及航天应用方面都有不少研究［8-12］。

由3 个连杆（其中第1 个连杆可视为航天器本体）、2 个关节的2 自由度机械臂是最简单的机械臂构型。这种机械臂运动关系相对简单，逆运动学可以采用解析方法求得封闭解。本文以此类型机械臂为例，用实验方法验证输入整形方法对弹性体转运过程的振动抑制效果，探讨其在空间机械臂操控中的应用潜力和实施方案，并就相关数学和力学问题进行了梳理，例如阐述了整形器归一化条件能使得整形后的速度函数具有总行程不变的特性。

1 机械臂(逆)运动学和输入整形方法

1.1 2 自由度机械臂的运动学和逆运动学

验证试验使用的2 自由度机械臂，基本构型及参数如图1 所示。机械臂原点位于o1点，双臂长度分别为L1和L2。模拟卫星的重物通过弹性缓冲器安装在末端o2点。2 自由度机械臂的末端只能限制在平面内运动，描述整个系统运动的自由度为2，后臂与水平轴的夹角θ1以及前臂相对于后臂的夹角θ2作为广义坐标。

图1 2 自由度机械臂示意图Fig.1 Schematic diagram of the mechanical arm with two degrees of freedom

根据广义坐标θ1、θ2（肩关节和肘关节的转动角度）计算末端笛卡尔坐标(x，y)，称为机械臂运动学。对于2 自由度机械臂，写出如下笛卡尔坐标与广义坐标的运动学关系：

根据笛卡尔坐标(x，y)计算关节转动角度θ1，θ2，称为逆运动学。一般情况下，逆运动学并不是唯一的。

如图2 所示，机械臂末端位于o2=(x，y)点。记o0与o2之间的距离为d，线段o0o2的极角为θ，后臂、前臂与线段o0o2的夹角分别为α、β。利用余弦定理可求得方程（1）的两组解：

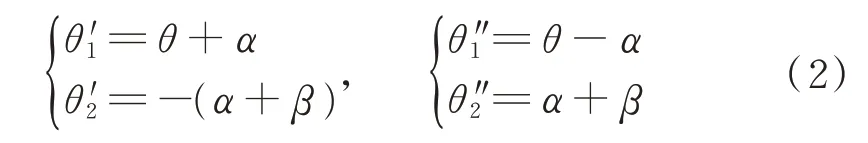
式中：

式（1）的逆运动学求解也可以采用数值求解方法，比如Newton 迭代法［13］。给定笛卡尔坐标(x*，y*)，估计一组广义坐标的初值，Newton的迭代法格式为

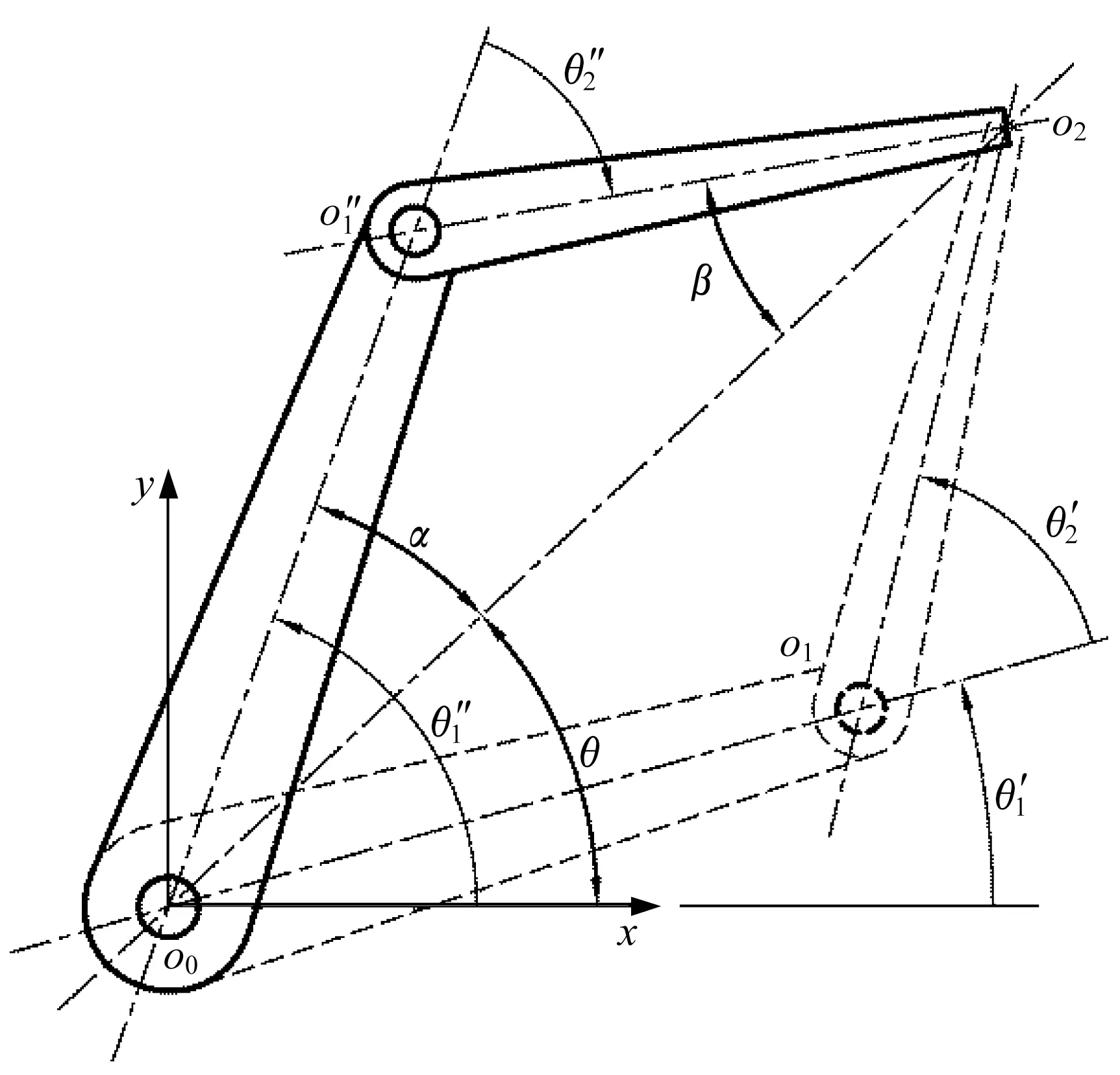
图2 2 自由度机械臂逆运动学的多解性Fig.2 Multiple solutions for the inverse kinematics of the mechanical arm with two degrees of freedom

式中：Jacobi 矩阵

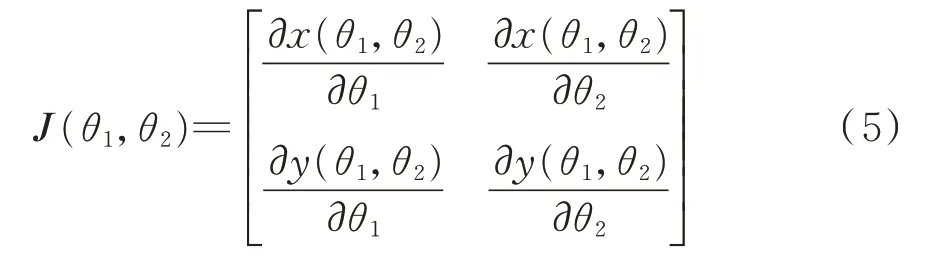
在迭代收敛的情况下有

行程设计要求在T时刻内，将机械臂末端从笛卡尔坐标为p0=(x0，y0)的起点移动到笛卡尔坐标为pn=(xn，yn)的终点上。常用的行程设计有笛卡尔坐标设计方法和关节转角设计方法。

笛卡尔坐标行程设计法选择直线运动实现机械臂末端从p0到pn的运动，期间经历匀加速、匀速和匀减速3 段变速直线运动。在ti时刻（i=0，1，…，n），根据直线运动关系容易算出机械臂末端的位置pi，其中，ti=iT/n。然后再根据逆运动学，依次计算2 个关节的转角θ1i和θ2i。

关节转角行程设计方法相对简单，2 个关节的转角行程可以独立设计。对于关节1，根据逆运动学计算得到起点和终点处的转角θ10和θ1n，再对起始、停止时刻的速度和加速度予以适当的约束，例如令，于是就能确定一段以5 次多项式表示的关节1 的转角函数θ1(t)。关节2转角行程的设计方法完全相同。采用关节转角设计的行程只有在起点和终点处的笛卡尔坐标是可控的，行程中的笛卡尔坐标只能由运动学式（1）计算，通用性不如采用笛卡尔坐标的行程设计方法。本文将要介绍的输入整形验证试验将采用笛卡尔坐标设计的行程。

1.2 机械臂末端行程的输入整形

作者将输入整形方法应用于航天器在调姿、变轨过程中的柔性附件振动抑制［14-15］。所谓输入整形器，就是由弹性结构m对固有频率和模态阻尼所确定的2m个常数a1，a2，…，a2m以及一个延时量ΔT。施加在结构上的外力函数f(t)经过整形后新的形式为

步骤1根据机械臂末端的起点p0和终点pn，将速度函数v(t)选择为典型的匀加速、匀速和匀减速梯形变速过程。

步骤2对函数v(t)进行整形，得到整形后的速度函数。

步骤3用数值求积法，由速度得到经过整形后的机械臂末端的笛卡尔坐标

步骤4用逆运动学方法，由笛卡尔坐标求得两个关 节的转角 函数。

由于被整形的速度函数满足条件

即函数v(t)在区间[0，T]以外都等于零，而且整形器常数还满足关系式（8），那么由整形过程式（7）可得

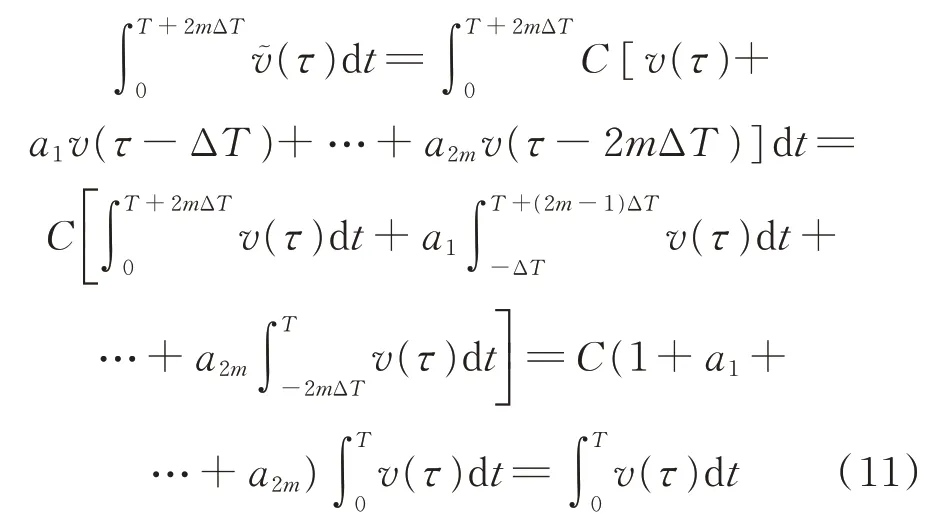
说明对整形后的速度函数进行积分，得到的运行距离与未经整形的结果相同，经过整形后的行程能保证机械臂末端到达相同的终点。

2 机械臂行程及整形设计

2.1 整形器的设计

试验使用的2 自由度机械臂由2 个臂长度分别为0.30 m 和0.25 m 的直杆构成，如图3 所示。后臂通过减速比为18∶1 的转台（肩关节）连接到支座上，前臂通过相同减速比的转台（腕关节）与后臂连接。模拟卫星的重物通过弹性缓冲器安装在前臂的末端，并在重物上安装了低频加速度传感器。

图3 输入整形验证试验的2 自由度机械臂Fig.3 Mechanical arm with two degrees of freedom for input shaping validation test

轻微扰动重物，由加速度传感器测得的自由振动响应信号如图4所示。数据的采集频率为1 000 Hz，采样时间4 s，信号经过上限为6 Hz 的2 阶Butterworth 低通滤波。由于实验的目的在于对比输入整形对机械臂运行振动的抑制效果，因此，在实验中仅测量加速度输出的电压信号v(t)（V），而没有标定加速度的绝对量（g或者m/s2）。

图4 重物受扰动后的自由振动响应Fig.4 Free vibration response of a heavy object after perturbation

对图4 的加速度信号v(t)作快速Fourier 变换（FFT），结果V(ω)如图5 所示（散点×）。

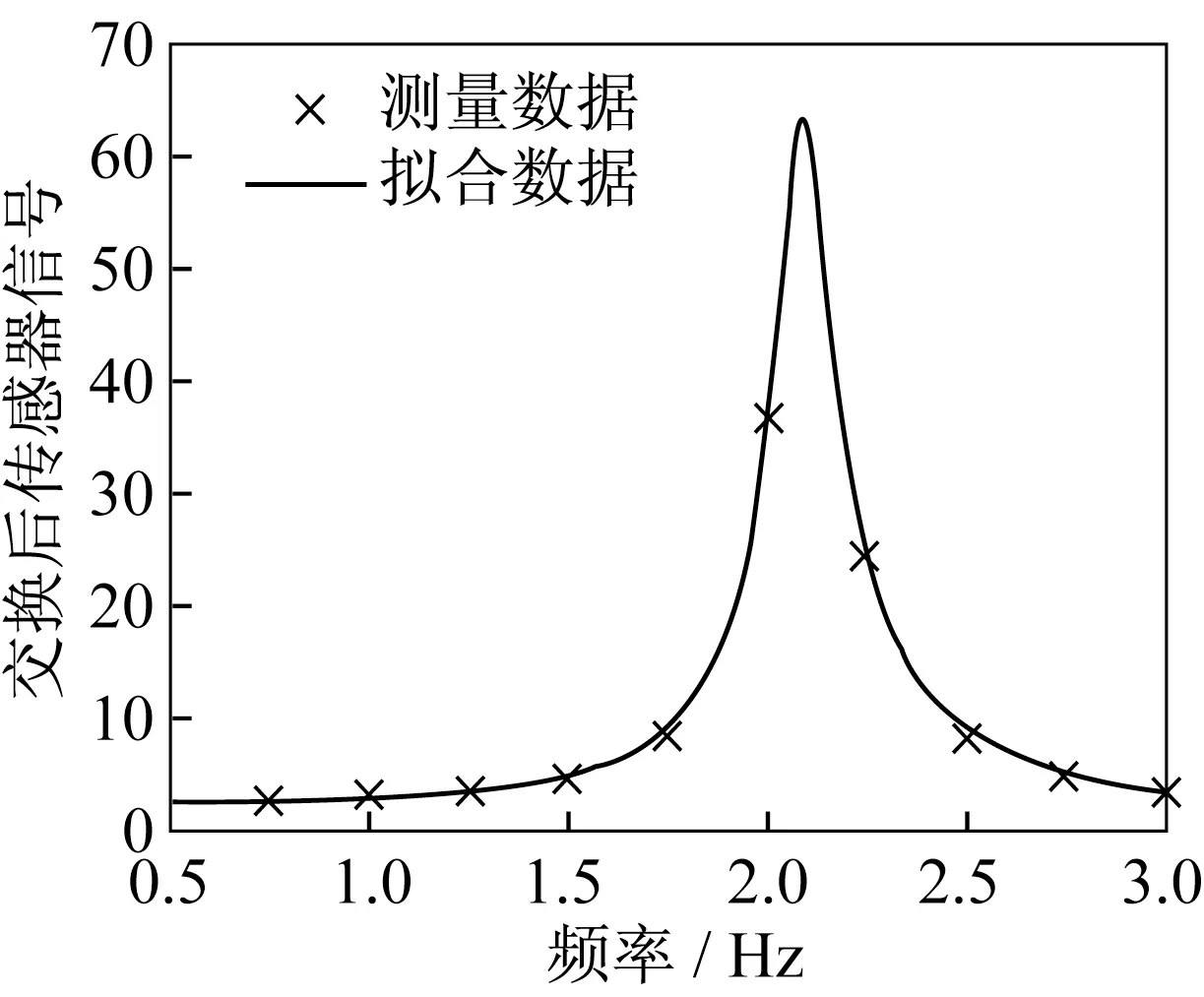
图5 加速度响应的FFT 变换结果Fig.5 FFT results of the acceleration responses

由于A(ω)仅用于分析结构的固有频率和阻尼比，因此，图5 中没有标出纵轴的单位。采用有理多项式逼近方法［16-17］，对函数V(ω)在频率区间[0.5，3.0]Hz 进行拟合，得到

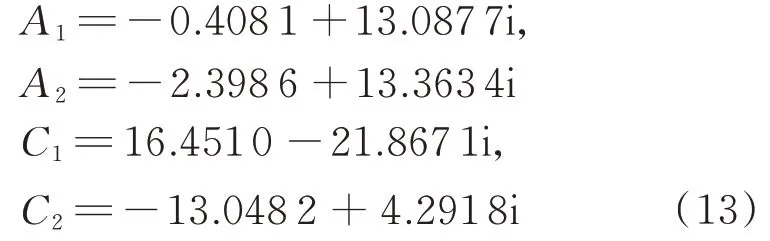
绝对值|V(ω)|的拟合效果如图5 中的粗实线。

由式（12）可见，模拟卫星的重物安装在机械臂后，构成的组合体的固有频率和阻尼比分别是

搜索最小延迟量ΔT的时间增量取为Δt=0.025 s，根据式（14）中的频率和阻尼参数，得到设计结果为

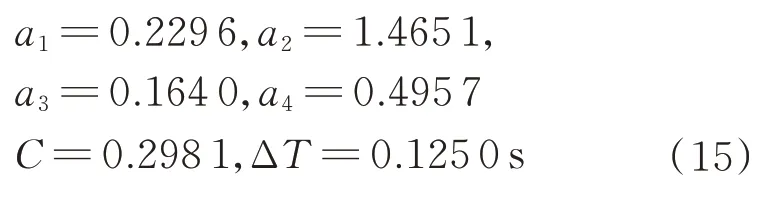
2.2 行程设计和整形

机械臂运行的起点设置在笛卡尔坐标为p0=(384.8，-366.5)mm 的位置上，对应的关节转角广义坐标是(-30°，-30°)。终点位于pn=(384.8，366.5)mm 的位置上，对应的关节转角广义坐标是(57.209°，-30°)。起点与终点之间的距离为733.01 mm，轨迹如图6（点划线）所示。笛卡尔坐标与极坐标的关系不是一一对应的，终点pn的极坐标也可以表示为(30°，30°)，但是在这个极坐标表示下机械臂（粗实线）末端无法从(-30°，-30°)连续运行到(30°，30°)。

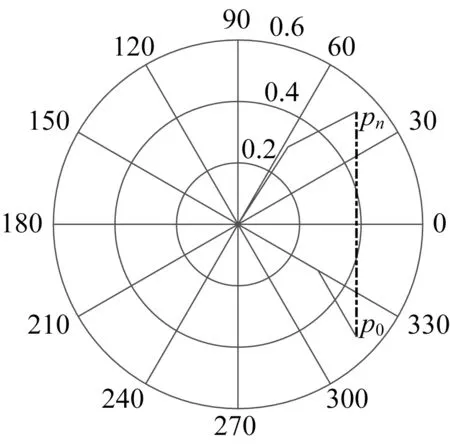
图6 机械臂的运动轨迹Fig.6 Operation route of the mechanical arm

给定起点和终点的坐标后，笛卡尔的行程设计由Matlab 工具箱Robotics Toolbox 完成，结果如图7所示。在图7 的上方，实线表示机械臂末端与起点距离随时间变化的函数，虚线表示机械臂末端运行速度随时间变化的函数。在图7 的下方，实线、虚线分别表示机械臂肩关节和肘关节的转角函数。

图7 行程的笛卡尔坐标设计结果Fig.7 Route design results in Cartesian coordinate

选用整形器式（15）对图7（上方）虚线所示的梯形速度函数进行整形，得到新的速度函数如图8（上方）的虚线所示。再对整形后的速度函数积分，得到的路程函数如图8（上方）的实线所示。通过逆运动学求解，可从笛卡尔坐标下的行程得到关节转角随时间变化的函数，如图8（下方）。这部分工作借助Matlab 工具箱Robotics Toolbox 实现。

图8 整形后的行程和关节的转角函数Fig.8 Functions of routes and rotation angles of joints after input shaping

3 机械臂行程输入整形的振动抑制效果

按照整形前后关节转角的时间函数图7（下方）和图8（下方）驱动2 自由度机械臂，整个运行过程中加速度传感器记录下的响应信号如图9 所示。机械臂行程经过整形后，组合体上加速度传感器所测得的最大响应幅值是0.005 093 V。未加整形行程时的最大响应幅值测量结果是0.013 080 V。输入整形方法将最大响应的幅值抑制到原来的39%。

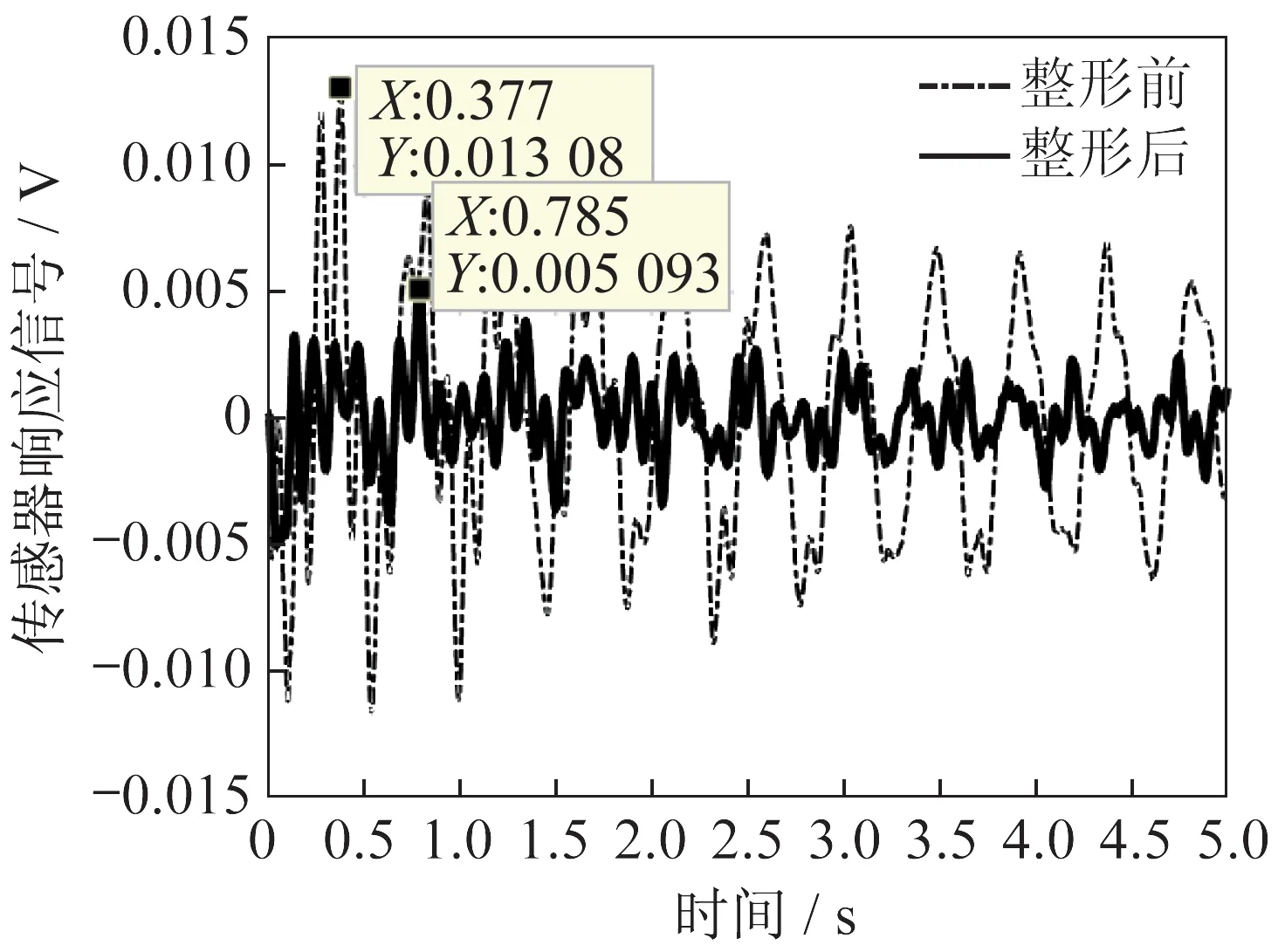
图9 输入整形方法对笛卡尔坐标表示下行程的振动抑制效果Fig.9 Effects of vibration suppression to the routes by the input shaping method in Cartesian coordinates

4 结束语

输入整形技术本质上是对设定的运动历程进行滤波，通过对搬运过程中机械臂的位移-时间历程进行整形，使搬运对象在机械臂的控制下沿整形后的运动历程搬运，将有望达到振动抑制的目的。该技术最大的益处是能完全利用既有的设备，无需增加额外结构或机构的质量。论文以三连杆二关节的2 自由度机械臂为例，进行了行程和输入整形设计，将整形后的动态响应与逆运动学的解析结果比较，发现输入整形方法可以大幅降低机械臂的最大响应幅值，达到了振动抑制的目的，证明了方法的有效性。该方法不仅可以拓展到7 自由度机械臂，而且对空间站大型机械臂末端振动抑制也有直接参考意义，具备空间大型柔性结构基座机器人在轨精细控制的应用前景。