空间伸展臂折展单元运动学分析

（南京航空航天大学 航天学院，江苏 南京 210016）

0 引言

随着航天技术的不断发展，航天事业对星载天线的需求与日俱增，连接天线与卫星本体的伸展臂已成为了航天技术重要研究对象之一。空间伸展臂主要分为杆状伸展臂、盘压杆式伸展臂、铰接桁架式伸展臂、张拉整体式伸展臂等［1］。其中，铰接桁架式伸展臂具有高收纳率、高刚度、高强度、高精度等特点［2］，该类型伸展臂仍是国内外研究重点。其可分为可折叠铰接四边形桁架伸展臂、可折叠铰接三角形桁架伸展臂、剪切式伸展臂、索杆铰接式伸展臂等［1，3］。可折叠铰接三角形桁架伸展臂较其他铰接方式具有结构简单、收展比高、重量轻等更多优点，近年来备受关注［4］。

目前，折叠铰接式伸展臂FASTM 和ADAM 应用最为广泛，美国NANM 的折叠铰接式伸展臂技术已十分成熟，国内对折叠铰接式伸展臂技术在力学分析和结构设计的理论、试验和仿真等方面均有重大突破［5-7］。文献［8］提出了一种三角桁架铰接伸展臂，对其进行力学分析。文献［9］提出一种恒力矩弹簧为驱动源的三角桁架支撑机构，分析伸展臂单元的运动特性，建立等效连续介质模型分析伸展臂动力学特性。文献［10］运用参数化思想建立有限元模型，对三角桁架折展式伸展臂进行结构优化。文献［11］利用螺旋理论分析可展桁架的运动特性，验证了单自由度桁架的正确性。文献［12］应用螺旋理论分析四棱柱型伸展臂运动特性和收展稳定性能。

1 可折展三角桁架式空间伸展臂的简介

可折展三角桁架式空间伸展臂主要由三角板、板间铰链、杆间铰链、折展杆、底板构成。其中，板间铰链和杆间铰链都设有驱动弹簧和锁紧装置。折展单元有3 个支链，每条支链有3 个旋转铰链，由弹簧驱动实现折展单元的展开。初始状态为压紧收拢状态，解锁后开始展开，完全展开后锁定。展开锁定后，形成稳固的刚性伸展臂结构。

图1 可折展三角桁架式空间伸展臂示意图Fig.1 Schematic diagram of the deployable triangular truss space deployable mast

2 空间伸展臂的折展单元的位置分析

伸展臂的折展单元结构原理图如图2 所示，由定三角板、动三角板和三条支链组成。

图2 折展单元的原理图Fig.2 Schematic diagram of the deployable unit

折展单元的完全收拢为θk1=0°，完全展开为θk1=90°，该折展单元有一个自由度，运动平稳。

以折展单元的一个支链为例进行分析，已知动、定三角板是边长m的等边三角形，支链的杆长为l。根据几何关系可以看出，动三角板与定三角板关于平面ABC对称，可以得到如下折展单元的运动约束方程：

每个支链旋转角都满足如下方程：

式中：k=1 为支链A；k=2 为支链B；k=3 为支链C。

同时满足式（1）和式（2），则定三角板与动三角板在运动过程中始终平行，即

货币资金是重要的企业资产，在正常生产经营过程中起关键性的作用，是企业关注的重点资产之一，而正由于货币资金的重要性和流动性，货币资金舞弊现象也常有发生。加强货币资金的内部控制，对于保证资金安全,提高资金运营效率,促进企业持续健康发展起着非常重要的作用。

由式（2）可知，确定支链的θk1即确定了支即链位姿；由式（3）可知，确定了θ11即确定了θ21、θ31，故确定θ11即确定了三角板的位姿。

基于以上折展单元的几何特性以及建立的折展单元运动约束方程，运用D-H 法的齐次变换矩阵对其进行正逆位置，利用螺旋理论对其进行正速度分析。

2.1 正位置分析

对折展单元的正位置分析，即位置角θ11作为输入量，求解动三角板的位姿。为更好描述动三角板的位姿，以中心点的运动代替。

建立如图2 所示的笛卡尔坐标系O（X，Y，Z），以A1B1中点为坐标原点，X轴正方向从原点O指向B1，Z轴正方向从原点O指向C1，Y轴正方向满足右手定则。在转动副上建立当前节点局部动坐标系Oj，下一节点的局部坐标系Oj+1，局部坐标系之间的齐次变换通式为jTj+1，

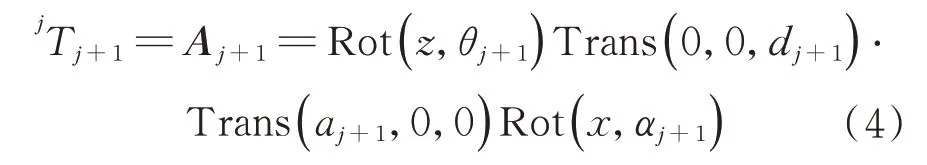
式中，θj+1为Oj+1绕Oj的Z轴的旋转角；dj+1为Oj+1沿Oj的Z轴的平移距离；aj+1为Oj+1绕Oj的X轴的平移距离；αj+1为Oj+1绕Oj的X轴的旋转角。

3 条支链运动平面的关于坐标系O的XOY平面变换矩阵的通式为

式中：βk为支链所在运动平面与坐标系O的XOY面的夹角。

根据折展单元的几何性质可得出A1、B1、C1的坐标，结合平面变换矩阵与齐次变换矩阵，可求得在笛卡尔坐标系下各节点坐标Pk(j+1)，最终确定动三角板O'的位置为

2.2 逆位置的分析

对折展单元的逆位置分析，即O'运动作为输入，求解位置角θ11。坐标系仍采用O（X，Y，Z），在各转动副上建立当前节点局部动坐标系，下一节点的局部坐标系，局部坐标系之间的齐次变换通式为，各支链平面变换通式为=Trk。结合平面变换矩阵与齐次变换矩阵，可求得各节点坐标，进而确定θ11，

2.3 正速度分析

对折展单元的正速度分析将位置角θ11作为输入，求解O'的速度螺旋V=(ω；V0)T。折展单元如图2 所示，将每个支链简化为一个开环运动链，其运动轴线记作单位螺旋，则每个支链的运动螺旋可表示为

则动三角板的速度螺旋与第k支链的3 个瞬时单位螺旋的关系为

式中：ω=(ωx，ωy，ωz)为动三角板相对于定三角板的角速度；V0=(V0x，V0y，V0z)为点O'的线速度。则式（12）可以简化为

由折展单元的运动特性可知同支链上的各运动关节的运动轴线相互平行，即支链上各运动关节的单位螺旋是相互平行的。取一经过原点且与运动螺旋方向平行的螺旋记做，根据两相交或平行螺旋的互易积为0，则与动三角板的速度螺旋V做互易可得到如下公式的3 个方程：

在第B、C支链上取一平行于的螺旋，

取一过点A3方向为A3A2的单位螺旋记为$f3，将螺旋$f3与动三角板的速度螺旋V做互易可得到如下1 个方程：

将式（14）、式（16）、式（18）联立，得到6 个方程，可求解出动三角板的速度螺旋V的6 个未知参数，确定动三角板O'的正速度。

3 仿真试验及结果分析

举例说明上述方法的应用，考虑折展单元的几何特点，取折展杆长n=90 mm，三角板的边长m=100 mm，输入量主动关节驱动角θ11=，折展单元的展开过程如图3 所示。

图3 折展单元的展开过程Fig 3 Deploying process of the deployable unit

将预设的参数代入D-H 法建立的正逆位置解中，借助软件Matlab 的“solve”函数计算出理论结果，得出动三角板中心点O'的位置曲线。为更好说明本文方法的正确性，借助软件ADAMS 仿真计算折展单元的正运动的位置，代入相同预设参数得到ADAMS 仿真模型。将理论计算结果与仿真计算结果进行比较，如图4 所示。图4 中虚线曲线为理论计算结果，实线曲线为ADAMS 仿真计算结果。从图中可以看出，理论计算结果与仿真计算结果重叠，验证位置分析方法的正确性。

将预设的参数代入螺旋理论建立的速度分析正解中，利用软件Matlab 求解动三角板中心点O'的运动速度，得到动平台O'的速度变化曲线。同样，将相同的参数代入ADAMS 软件中进行仿真计算，去验证速度计算结果的正确性。将理论计算结果与仿真计算结果进行比较，如图5 所示。图5 中的虚线曲线为理论计算结果，实线曲线为ADAMS 仿真计算结果，从图中可以看出理论计算结果与仿真计算结果基本一致，本文提出计算动平台O'运动位置的方法可以准确计算出动三角板中心点O'的运动速度。

图4 仿真计算与理论计算位移变化对比图Fig 4 Comparison diagram of the displacement changes obtained by the simulation and theoretical calculations

图5 仿真计算与理论计算速度变化对比图Fig 5 Comparison diagram of the velocity changes obtained by the simulation and theoretical calculations

结合图4 和图5 曲线的变化，可得动三角板中心点O'的运动速度大小与位移变化曲线的曲率正相关，则可通过速度曲线的曲率估算加速度。

4 结束语

本文对可折展三角桁架式空间伸展臂单元进行运动学分析，运用D-H 法分析了折展单元正逆位置，利用螺旋理论对折展单元进行正速度分析。借助ADAMS 对折展单元进行运动学仿真计算，对比仿真计算结果与本文方法的计算结果基本一致，验证了本文方法的正确性。计算结果可看出，折展单元动三角板中心点的位移和速度都只在Y轴方向上有变化，其他方向的运动分量都为0，说明了折展单元运动的单一性，能够满足空间折展机构的功能需求，为空间伸展臂的进一步研究提供参考依据。