数学模型在解三角问题中的应用

◇ 山东 杜海龙

构造是一种重要的数学思维方法，它是创造力的较高表现形式，是高考考查的热点．在解题中应注意依据题目特征类比相关知识，通过构造数学模型来促进问题的解决，从而培养思维的创造性．构造时，需要跳出题外，高屋建瓴，方可遂愿．本文举例说明构造数学模型在求解三角函数问题中的应用．

1 构造对偶模型

例1求值

解析

①＋②，得

①－②，得

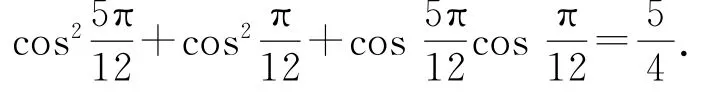
点评

由于所求代数式是二次齐次式且只含余弦函数，而余弦函数和正弦函数一般是成对出现的，因此可考虑构造相应的正弦函数来求解．

例2求的值．

解析

设所求的式子为

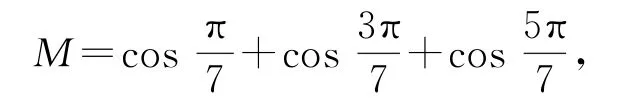
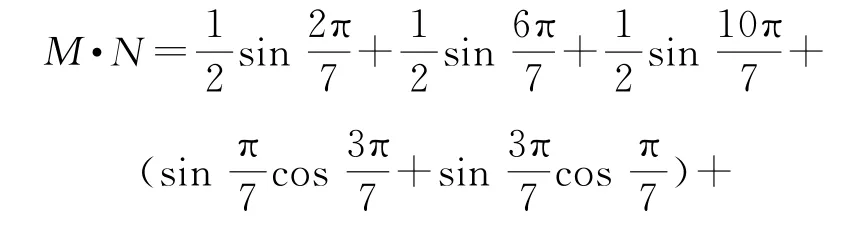
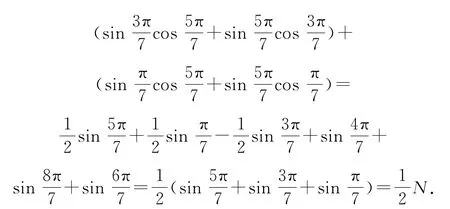
点评

在对偶式的构造上，要注意，有时是互余对偶，有时是和差对偶，有时是互倒对偶……对偶的灵活性与求解的巧妙性构成了一道和谐、美丽的风景．

2 构造函数模型

例3已知α，β为锐角，且，则

下列结论中正确的是（ ）．

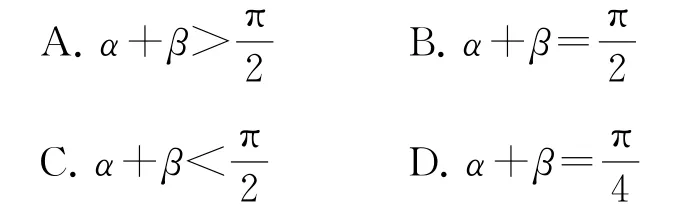
解析

点评

本题通过构造函数，利用函数的单调性将“角”的关系进行转化．

例4已知，且

求cos（x＋2y）的值．

解析

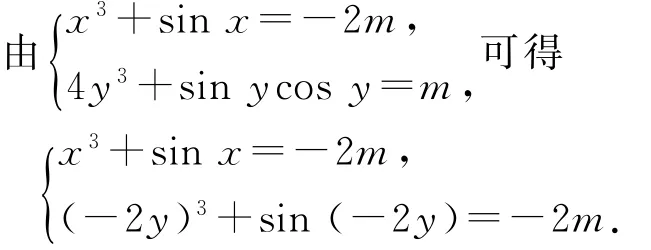
构造函数f（t）＝t3＋sint，易知它是上的单调递增函数．

点评

本题通过构造函数，利用函数的单调性进行求解，很是巧妙．

3 构造向量模型

例5若α，β∈（0，π），求满足等式cosα＋的α和β的值．

解析

原等式可化为（1－cosβ）cosα＋sinβsinα＝

构造向量a＝（1－cosβ，sinβ），b＝（cosα，sinα），则

因为（a·b）2≤|a|2·|b|2，所以

点评

本题将条件等式在变形的基础上构造两个向量，并运用向量的数量积运算和性质求解，体现了向量知识应用的广泛性．

4 构造数列模型

例6证明，其中0，1，2，…，n，λ∈Z．

证明当n＝1时，即证由三角函数的知识可以证明此式成立．由此我们可以构造一个数列递推式

再利用累加法获证．

点评

寻求项与项之间的一般关系，构造数列递推式证明，体现了数学中的以退求进、特殊到一般的思想方法．

5 构造复数模型

例7已知x，y，z∈R，且

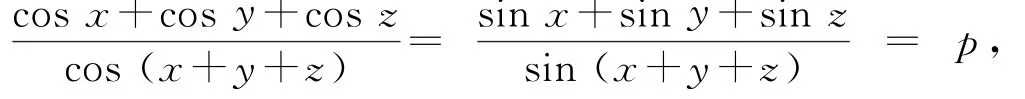
求证:

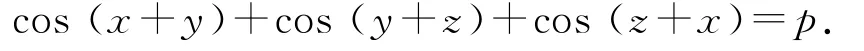
证明设复数α＝cosx＋isinx，β＝cosy＋isiny，γ＝cosz＋isinz，且¯α，¯β，¯γ分别是α，β，γ的共轭复数，则α¯α＝1，β¯β＝1，γ¯γ＝1．

由等比定理，得

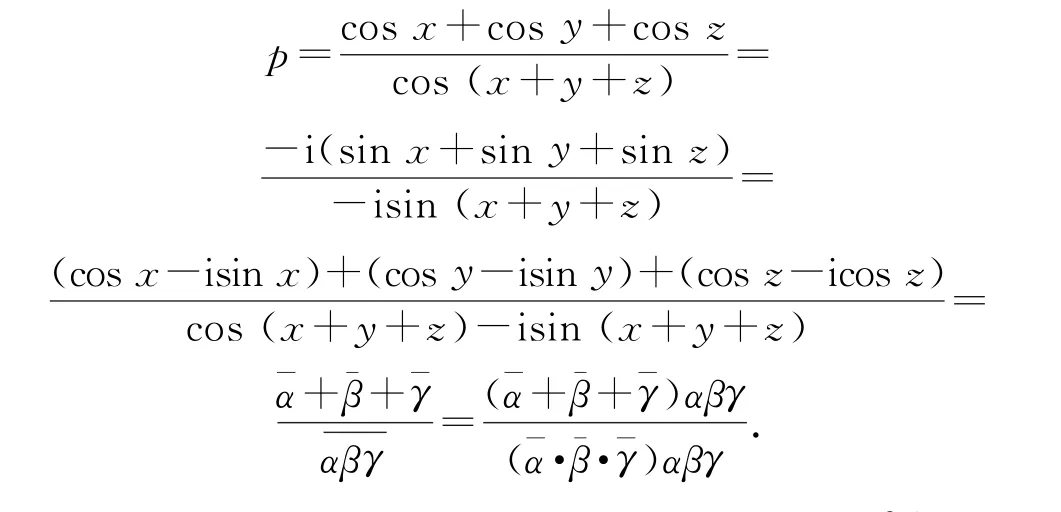
由已知，p显然为实数，所以sin（x＋y）＋sin（y＋z）＋sin（z＋x）＝0．故

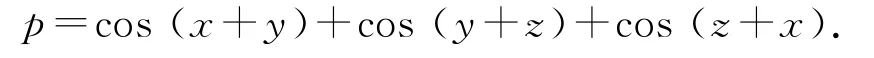
点评

由于复数有三角式，对于具有对偶形式的三角问题，通过构造复数的三角式来求解较为方便有效．

6 构造解析几何模型

例8已知求证:

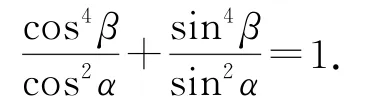
解析

本题初看起来关系式很整齐，但却很难找到条件与结论直接的逻辑关系，但仔细观察可以发现它与椭圆的标准方程很相似，因此可以构造椭圆模型

又在P2处的椭圆的切线方程为x＋y＝1，而点P1也在切线x＋y＝1上，由切点的唯一性知，点P1与P2重合．故cos2α＝cos2β，sin2α＝sin2β，即

点评

构造解析几何模型是实现数形转换的一种方法，它的应用范围较为广泛．本题利用点的坐标、曲线的方程的有关性质巧妙地寻找条件与结论间的逻辑关系进行证明．

7 构造三角模型

例9求函数的最大值和最小值．

解析求解本题最大的困惑就是去掉根号，仔细观察 sinx和可知sin2x＋，由此可以构造三角模型求解．

点评

本题通过构造三角模型，利用三角函数的性

质巧妙地摆脱了根号的困惑，使问题获解．