解答2020年高考向量问题的几种思维方式
◇ 山东 张颖枭
向量是高中数学的重要模块,在各省市的高考试题中主要考查向量的模、夹角、共线、垂直以及数量积等运算,常以客观题的形式出现,题小但思维量不小.向量问题的求解中除了要有扎实的基础以外,还要掌握各类思维方式.本文选取2020年高考中出现的部分向量问题,就问题求解中所用到的思维方式进行分析.
1 平方思维
向量运算中的关系a2=|a|2,实现了向量向数量的转化,因此问题中涉及向量的模的有关条件时可运用平方思维进行转化.
例1(浙江卷)设e1,e2为单位向量,满足,设a,b的夹角为θ,则cos2θ的最小值为________.
解析
设向量e1,e2的夹角为φ,由,平方得
又a·b=(e1+e2)(3e1+e2)=4+4 cosφ,所以
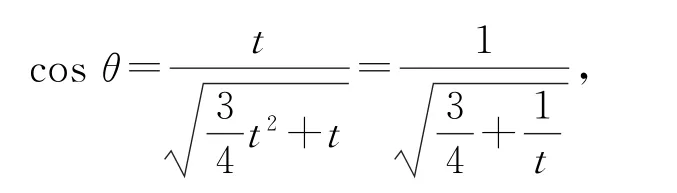
点评
本题求解中多次运用了平方思维,如cosφ,|a|,|b|的求解等.在求cosθ最值时,还运用了换元法及分离常数法.
2 基底思维
平面内不共线的两向量a,b,可表示任意向量c=λ a+μb(λ,μ∈R),则称向量a,b为一组基底.解题中借助基底思维可实现未知向量向已知向量及特殊向量的转化.
例2(江苏卷)在△ABC中,AB=4,AC=3,,点D在边AC上,延长AD至点P,使得AP=9,若(m为常数),则CD的长度是________.
解析

图1
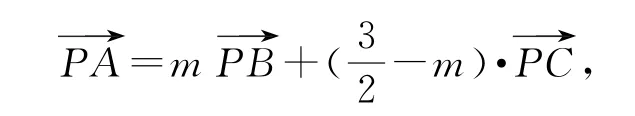
因为B,D,C三点共线,所以,解得.因为|PA|=9,所以|PD|=6,|AD|=3.在,由余弦定理,得|AD|2=|AC|2+|CD|2-2|AC|·|CD|cos∠ACD,即,所以或0,经检验|CD|=0也满足条件,此时点D与C重合.
点评
向量的合成与分解均符合基底的原理.本题的解题思路源于向量三点共线的结论,求解中运用了解三角形的基本理论.
3 坐标思维
向量的坐标运算是向量代数性的重要体现,通过建立平面直角坐标系将几何问题代数化,从而利用函数、方程的性质求解.
例3(山东卷)已_知P是边长为2的正六边形ABCDEF内的一点,则的取值范围是( ).
A.(-2,6)
B.(-6,2)
C.(-2,4)
D.(-4,6)

图2
解析
如图2,以正六边形的中心O为坐标原点,BE所在的直线为x轴建立平面直角坐标系,则
设P(x,y),所以
点评
坐标法是实现向量问题代数化的重要途径,得出关于数量积的二元式,进而可运用线性规划求解最优解的知识得出结论.
4 构图思维
图形是向量几何性质的直观体现,向量的加、减、数量积运算均有其图形解释.某些向量问题的解答过程中,若能结合已知条件巧妙构造相应几何图形,则可有效简化求解过程.
例4(上海卷)已知a1,a2,b1,b2,…,bk(k∈N)是平面内两两互不平行的向量,满足|a1-a2|=1,且|ai-bj|∈{1,2}(其中i=1,2;j=1,2,…,k),则k的最大值为_______.___
解析
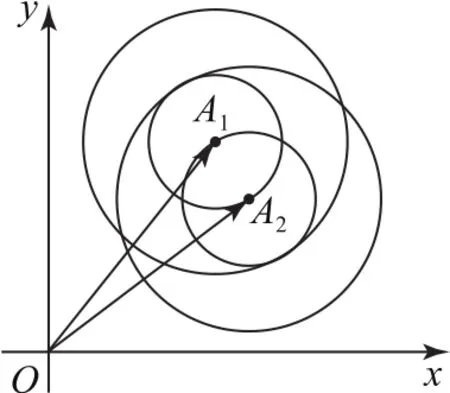
图3
由已知条件|a1-a2|=1,根据向量减法运算的三角形法则,可知点A1在以A2为圆心、1为半径的圆上,或点A2在以A1为圆心、1为半径的圆上,如图3所示.
同理|ai-bj|∈{1,2}可转化为以向量a1,a2的终点A1,A2为圆心,半径分别为1和2的圆,则圆的交点即为满足题意的向量bj的终点,因此,满足条件的点最多有6个,故k的最大值为6.
点评
模为定值的向量,则其终点在以起点为圆心、模为半径的圆上.因此涉及模为定值的问题可构造圆,利用圆的相关性质求解.

