解三角形中的最值与范围问题
◇ 江西 曾 伟
在高考数学中,解三角形中经常有两种题型,一种是三角形基本量的计算,如求角、边、面积等,属于基础常规题;另一种就是求最值或范围问题,相对前者而言,这类问题较难,学生不容易掌握.本文将从以下的例题和练习题中,寻求求解三角形中最值与范围问题的一般策略与方法.
1 解三角形中的最值问题
例1(2020年全国卷Ⅱ)△ABC中,sin2A-sin2B-sin2C=sinBsinC.
(1)求A;
(2)若BC=3,求△ABC周长的最大值.
解析
(1)在△ABC中,设角A,B,C的对边分别为a,b,c,则由正弦定理和已知条件得

由余弦定理,得
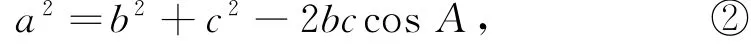
(2)方法1已知a=3,由正弦定理及(1)得

方法2由a=3,a2-b2-c2=bc,得9=b2+c2+bc≥3bc,所以bc≤3,当且仅当b=c时等号成立.又(b+c)2=b2+c2+2bc=9+bc≤12,所以b+c≤.因此△ABC周长的最大值为,当b=c(即)时取得最大值.
点评
此题第(2)问考查△ABC周长的最大值,方法1根据正弦定理结合已知条件将三角形周长表示为关于角B的三角函数,运用辅助角公式,结合角B的范围求得周长的最大值,该方法较为常规,体现了高考试题的基础性与稳定性.方法2运用了基本不等式,因为a已知,所以求三角形周长的最大值即转化为求b+c的最大值,最后转化为求bc的最大值,而bc的最大值可根据已知条件及基本不等式求得,该方法具有一定的技巧性,需要考生结合最终目标进行相应的转化.
例2在△ABC中,则AB+2BC的最大值为________.
解析
方法1因为B=60°,A+B+C=180°,所以A+C=120°,由正弦定理,得
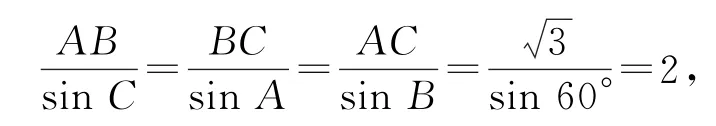
所以AB=2 sinC,BC=2 sinA,所以

方法2设AB=c,AC=b,BC=a,由余弦定理,得,所以a2+c2-ac=b2=3,设c+2a=m,代入上式消去c,得7a2-5am+m2-3=0,由Δ=84-3m2≥0,得,当时,符合题意,因此AB+2BC的最大值为
点评
方法2是值得我们思考的,如果是求AB+BC的最大值,那么可以完全照搬例1中的方法2,可是一旦变成求AB+2BC,我们就需要另寻他法了.
例3(2016年江苏卷)在锐角△ABC中,若sinA=2 sinBsinC,则tanAtanBtanC的最小值是_________.
解析
方法1因为sinA=2 sinBsinC,所以sin(B+C)=2 sinBsinC,两边同时除以cosBcosC,得tanB+tanC=2 tanBtanC,因为
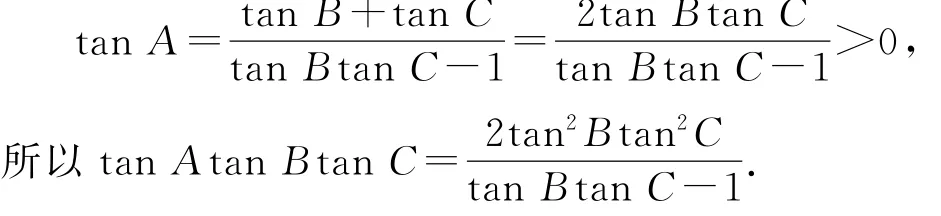
设x=tanBtanC-1>0,

当且仅当x=1(tanA=4)时,等号成立,故tanA·tanB·tanC的最小值是8.
方法2由已知条件得tanB+tanC=2 tanBtanC,则
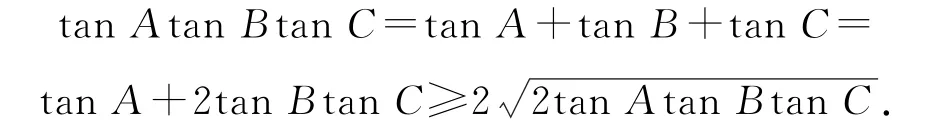
故tanAtanBtanC≥8,即其最小值为8.
点评
本题是2016年江苏卷填空题的压轴题,难度较大.方法1结合正切的诱导公式利用换元法将tanAtanBtanC化为的形式,其最值便一目了然.方法2用到了三角形中的恒等式tanAtanBtanC=tanA+tanB+tanC,再利用基本不等式得到最值,思路清晰,解法简捷.
2 解三角形中的取值范围问题
例4(2020年浙江卷)在锐角△ABC中,角A,B,C的对边分别为a,b,c,且
(1)求角B;
(2)求cosA+cosB+cosC的取值范围.
解析
(2)由A+B+C=π,得,由△ABC是锐角三角形,得由

得
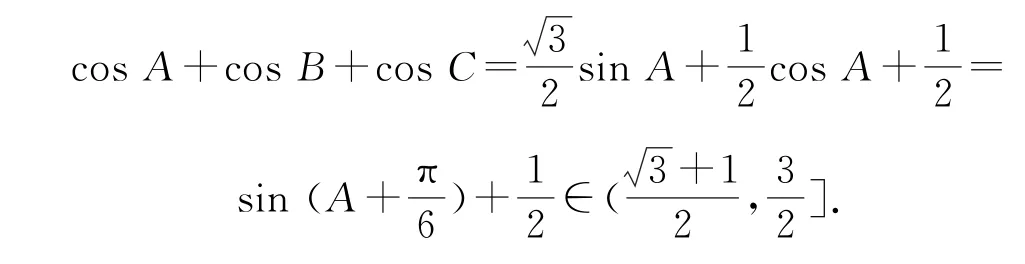
故cosA+cosB+cosC的取值范围为
点评
此题解法与例1解法的方法1相似,需要注意的是△ABC是锐角三角形,则只有角的范围准确才能得到正确取值范围.
例5(2019年全国卷Ⅲ)△ABC的内角A,B,C的对边分别为a,b,c,已知
(1)求B;
(2)若△ABC为锐角三角形,且c=1,求△ABC面积的取值范围.
解析

因为sinA≠0,所以.由A+B+C=π,可得,故
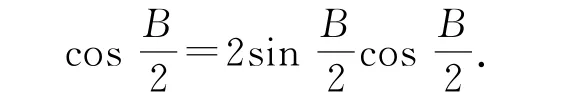
(2)方法1由c=1及,可知△ABC的面积.由正弦定理,得
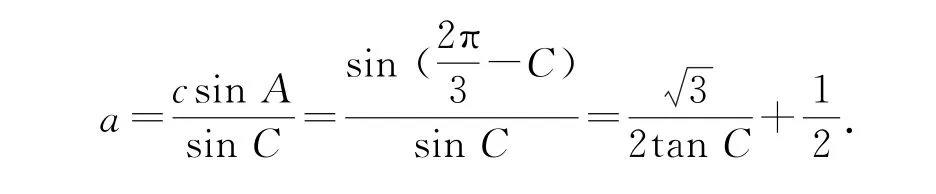
由于△ABC为锐角三角形,故,由,知,所以,故,从而,因此△ABC面积的取值范围是
方法2(极限思想、极端原则)如图1所示,AB=c=1,,若△ABC为锐角三角形,则点C位于DE之内,故a=BC∈(BD,BE),因为,所以

图1
由于△ABC的面积,因此其取值范围是
例6(2015年全国卷Ⅰ)在平面四边形ABCD中,∠A=∠B=∠C=75°,BC=2,则AB的取值范围是________.
解析
方法1如图2所示,连接AC,设∠BAC=α,则 ∠ACB=105°-α.由正弦定理,可得由于α<75°,且105°-α<75°,得α∈(30°,75°),所以故

图2
方法2(极限思想、极端原则)如图3所示,延长BA,CD交于点E,过点C作DA的平行线交AB于点F.平移AD,当点A与点D重合于点E时,AB最长.在△BCE中,由正弦定理,得


图3
平移AD,当点D与点C重合,点A与点F重合时,AB最短.在△BCF中,由正弦定理,得,所以
点评
由例5和例6可知,在三角形中求取值范围时要尽可能地利用已知条件,当要求的式子能用角的三角函数表示时,仅需根据已知条件确定角的范围即可;当能用边长表示时,需要借助正弦定理将边化为角,才可以更好地求取值范围.同时,利用极限的思想、极端原则给该类问题提供了一种新的思路,方法较新颖,值得反思与推敲.
3 训练巩固
以下精选几道习题,供读者练习巩固,希望读者解决该类问题的思路与方法能得到更进一步的升华.
练习1△ABC的三个内角A,B,C的对边分别为a,b,c,若B=2A,cosAcosBcosC>0,则的取值范围是( ).


练习2△ABC的三个内角A,B,C的对边分别为若a+b=4,则c的取值范围为( ).
A.(0,4) B.[2,4)
C.[1,4) D.(2,4]
练习3已知△ABC的内角A,B,C的对边分别为a,b,c,且,若c为最大边,则的取值范围是( ).
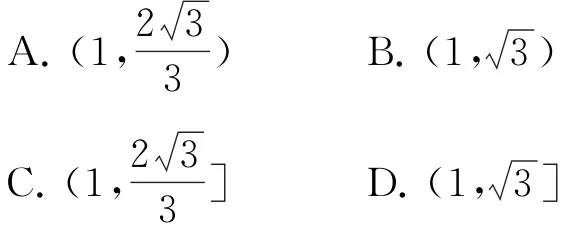
练习4若△ABC的面积为且∠C为钝角,则∠B=________;的取值范围是________.
练习5△ABC的垂心H在其内部,∠BAC=60°,AH=1,则BH+CH的取值范围是________.
练习6在△ABC中,a,b,c分别是角A,B,C所对的边,且2csinB=3atanA.
(2)若a=2,求△ABC面积的最大值.
练习7在△ABC中,角A,B,C的对边分别为a,b,c,△ABC的面积为
(1)若a,b,c成等差数列,试判断△ABC的形状.
(2)求a+c的取值范围.
解三角形中的最值与范围问题是高考数学的一类热点题型,几乎每年必考.通过以上的例题与练习题我们发现,解决该类问题的方法主要有统一化角,将问题转为三角函数值域问题,或是根据已知条件利用基本不等式求得最值.有时也需要用到极限的思想,通过考虑极端位置来确定取值范围.每种方法中都有需要注意的关键点,比如统一化角时一定要清楚角的范围,利用基本不等式时要注意等号成立的条件.通过此文,希望读者对解三角形中的范围与最值问题理解更深刻,思路更开阔,解题更灵敏.

