强基计划实施元年高校校考试题表现
◇ 北京 王慧兴(特级教师)
2020年是强基计划实施元年,笔者研究了北京大学、清华大学、复旦大学、中国科学技术大学、上海交通大学等著名高校强基计划校考试题,发现试题内容涉猎全面,大体上可分为6个层次,且试题突出表现出强基计划校考数学试题传承高校自主招生考试的命题风格,与高考保持鲜明互补.
1 衔接高考,检测基本技能
强基计划校考数学试题中存在与高考试题风格一致的题目,与高考衔接,旨在检测考生基础知识与基本数学技能,但这部分题目占比较小.因此,强基计划校考与高考互补又衔接.

表1
例1(中国科学技术大学校考试题)求所有的a∈R,使得函数f(x)=x3+ax2-x+1-a,满足|f(x)|≥|x|,∀x∈[-1,1].
解析
直接验证,可知x=-1,0,1对a不起限制
作用,则
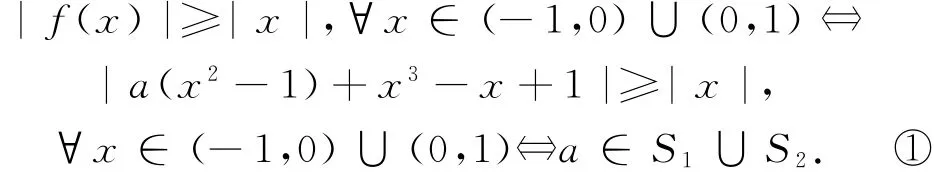
先求S1={a∈R|a(x2-1)+x3-x+1≤-|x|,∀x∈(-1,0)∪(0,1)}.

令正数t→0,得,所以实数a不存在,即S1=∅.
再求S2={a∈R|a(x2-1)+x3-x+1≥|x|,∀x∈(-1,0)∪(0,1)}.
∀x∈(-1,0)∪(0,1),都有a(x2-1)≥|x|-1-(x2-1)x,所以


综上,符合题意的实数a的取值范围是

点评
探究恒成立问题的参数取值范围是高考与强基计划校考的常考题型,但强基计划校考对参数情境设置较复杂,对考生有条理地分类讨论能力有更高要求.
例2(北京大学校考试题)正整数n≥3称为理想数,若存在正整数1≤k≤n-1,使得成等差数列,则不超过2020的理想数个数为( ).
A.40 B.41 C.42 D.前三个都不对
解析

所以n+2=l2(l∈N∗,l≥3)为完全平方数,即n=l2-2(l∈N∗,l≥3).由3≤n=l2-2≤2020,得5≤l2≤2022,则,故3≤l≤44,理想数n=l2-2共有42个.
综上,选C.
点评
本题以高中数学教材内容立意试题,引领考生深入变式探究.
2 开阔视野,拓展思维,增强灵活性
强基计划校考数学命题不会刻意回避陈题,不少题目源于过往的各级各类竞赛题或高校自主招生试题,留有过往试题的痕迹,属于推陈出新.

表2
例3(复旦大学校考试题)设若

则cos(x+2y)=________.
解析
对题设条件进行三角变换,得

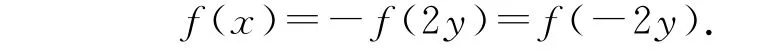

点评
本题是基于早期全国高中数学联赛试题的推陈出新.
例4(上海交通大学校考试题)用同样大小的正n边形平铺整个平面(没有重叠),若要将整个平面铺满,则n的值为________.
解析
题设条件等价于
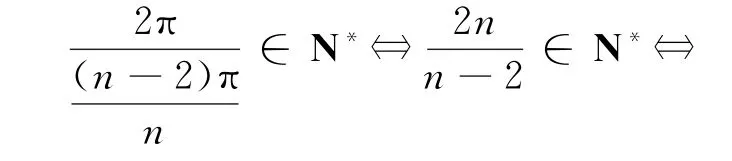
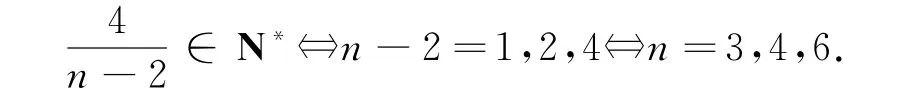
点评
本题源于2019年复旦大学自主招生考试的试题.
3 面向创新,新颖灵巧,检测快速反应能力
强基计划校考数学试题中常出现给出新概念、建立新运算、设置新结构的试题,以检测考生迅速、准确理解与运用的探究能力,题目设计新颖灵巧,突出代数灵活性,检测考生快速反应能力.

表3
例5(北京大学校考试题)函数的最大值是( ).
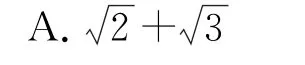

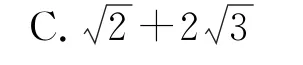
D.前三个答案都不对
解析
调整结构,得
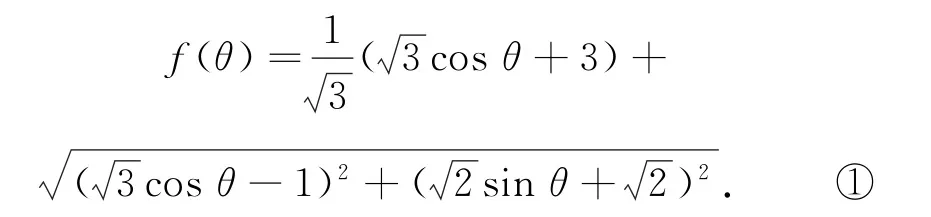

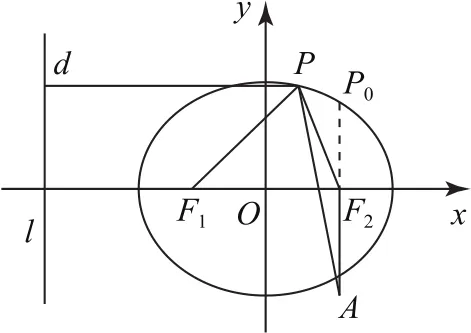
图1
点评
代数式灵活变形广泛地表现在代数式化简、求值、解方程、解不等式、探求最值等多个方面,以检测考生整体把握与快速反应能力.
例6(北京大学校考试题)设x,y,z,w满足x≥y≥w,且x+y≤2(w+z),求的最小值.
解析由题设条件将目标变量适度放缩,寻求下界,即

其中等号成立的条件是

点评强基计划校考试题继承自主招生的命题风格,对代数式灵活变形有较高要求.
4 突出高考弱化的或长期不考的内容
从强基计划实施元年高校的校考试题看,高校校考十分重视考生全面把握数学知识的学习能力,校考不像高考那样有明确界定不考的内容,而是全面检测考生数学素养与关键能力.强基计划校考注重在高考弱化处立意试题,以检测学生数学学习能力.

表4
例7(北京大学校考试题)对一切x,y>0,都有,则实数a的最小值是( ).
A.8 B.9 C.10 D.前三个答案都不对
解析
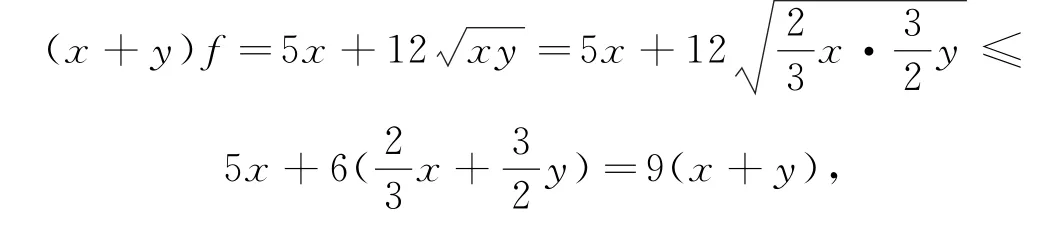
所以,f≤9,其中等号在时取到,故amin=9,选B.
点评
多元最值在高考中常以选考题的形式出现,通常用于检测二元、三元均值不等式或三维柯西不等式的简单应用,不需要平衡系数.但这些知识在强基计划校考中灵活性较强、难度较大.譬如,本题需要平衡系数,需要参数调控,引入a>0,
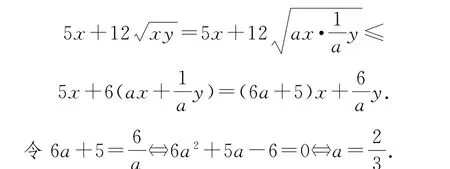
例8(中国科学技术大学校考试题)曲线f(x)=的离心率为________.
解析
所以,曲线C的方程为
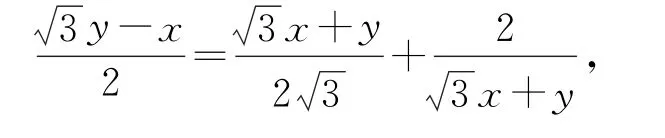
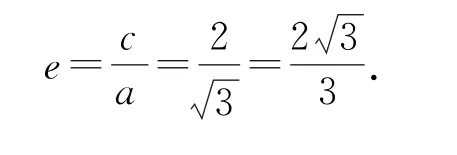

图2
点评
如果已经知道这个函数图象是双曲线,就不必再进行旋转了,直接按照公式计算,即

例9(北京大学校考试题)从☉O:x2+y2=4上一点作椭圆的切点弦,求切点弦围成的面积.
解析
如图3所示,过☉O:x2+y2=4上一点P(2 cost,2 sint)作椭圆的切线PA,PB(A,B为切点),则直线AB的方程为xcost+2ysint=1,这个直线系的包络线是一个椭圆,直线xcost+2ysint=1又是椭圆E′在点R(acost,bsint)处的切线,即,所以a=1,,故题设切点弦围成的包络线是椭圆E′:x2+4y2=1,其面积为
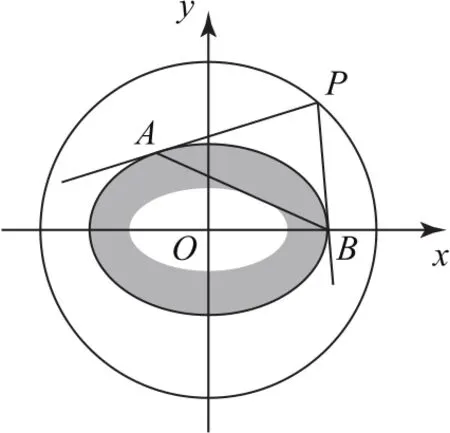
图3
点评
与圆锥曲线有关的动点轨迹早已是高考的弱化考点,但其在强基计划校考中常常出现,本题主要考查直线系的包络线——椭圆的面积计算.
例10(中国科学技术大学校考试题)已知

证明取,并且
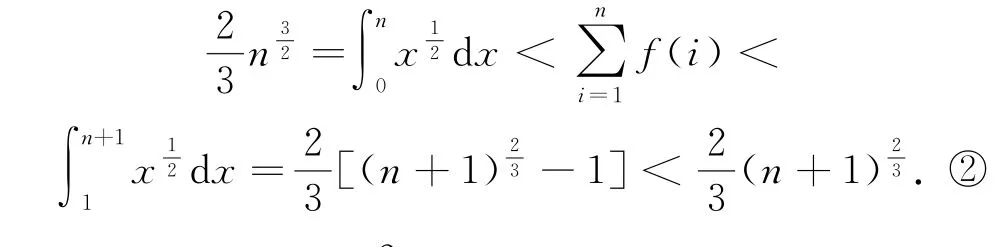

从而存在n∈N∗,满足

对这样的正整数n,题设不等式不成立.
综上,命题得证.
点评
高考检测了考生导数的应用能力,但极限、连续性与积分都不是高考内容.极限与连续性是微积分的基础,导数与定积分都是以极限定义的,也离不开连续性,尤其是定积分的根本算法——微积分基本定理,它是17世纪最伟大的数学成就.因此对极限与定积分,强基计划校考命题会持续关注.
例11(清华大学校考试题)sin(arctan1+
解析

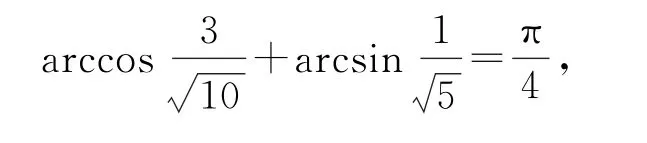
故得
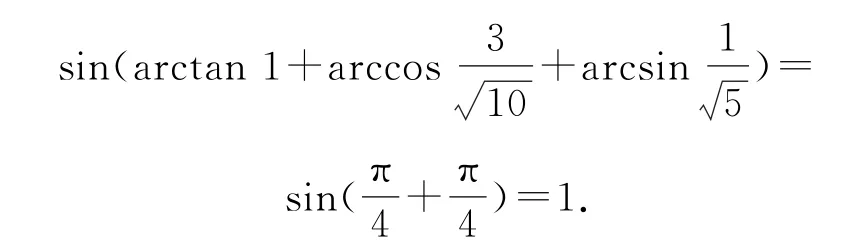
点评
现行高中数学教材中只提及了反三角函数的概念,因此,反三角函数的性质及其运算高考已长期不考,但反三角函数求值在强基计划校考中常常出现.
例12(北京大学校考试题)设a,b,c,d是方程x4+2x3+3x2+4x+5=0的4个复根,则的值是( ).


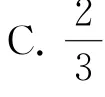
D.前三个答案都不对
解析
按题意,a+b+c+d=-2,ab+ac+ad+bc+bd+cd=3,abc+abd+acd+bcd=-4,abcd=5,所以
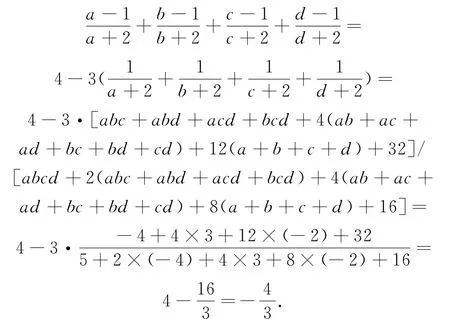
故选A.
点评复数是高考长期弱化的内容,在高考中,复数的考查仅停留在四则运算与模和共轭概念的层面.但强基计划校考对复数的检测力度比较大,譬如共轭与模的性质、复数与方程、复数与三角、复数与几何、复数与多项式、单位根性质等都会出现.
例13(上海交通大学校考试题)从2个红球、3个黑球、5个白球中任意取出6个,有________种不同取法.
解析同色球之间无区分,分类十分复杂,因此可用母函数构建计数方法,取球的方法数就是以下多项式中6次项系数和,即
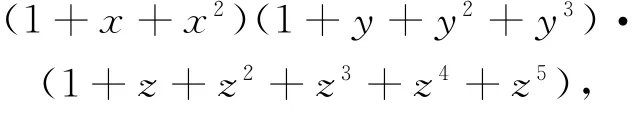
再简化一下,就是以下单变量多项式中x6的系数和,即

其中x6的系数为
点评如果同色球之间也有区别,则应分11类计数,即.高考中组合计数考查难度较低,课标反复强调不要搞“基于组合计数的概率计算”,但强基计划校考试题考查内容与之互补,组合计数与概率是高频考点,而且难度较大,对分类能力要求较高,对计数转化方法要求也较多,仅靠列举法不能满足计数要求.
5 突出高考根本不考的内容
这些内容突出表现在几何计算、组合计数、推理、极值与构造、整数分析等方面,也包括思维方式上的差异,题目立意精巧,对阅读理解与快速反应能力要求高.

表5
例14(中国科学技术大学校考试题)给定整数n>1,在(1,2,…,n)的全排列(a1,a2,…,an)中,称ai<aj(1≤i<j≤n)为一个顺序对,则一个全排列(a1,a2,…,an)中顺序对个数X是一个随机变量,则E(X)=________.
解析
(1,2,…,n)的全排列(a1,a2,…,an)共有n!个,每一个(a1,a2,…,an)出现的概率都是,所以

点评
配对与分组是典型的组合思维方法,高考中很少涉及组合分析能力.
例15(复旦大学校考试题)方程3x+4y+12z=2020的非负整数解个数是( ).

解析
因为3x+4y+12z=2020,所以4|x,记x=4x1(x1∈N),方程化为3x1+y+3z=505;模3,得y=1(mod3),记y=3y1+1(y1∈N),方程化为x1+y1+z=168.所以原方程的非负整数解(x,y,z)的个数等于非负整数组(x1,y1,z)的个数,即,选C.
点评关于不定方程正整数解或非负整数解的个数,有一个典型结论:方程x1+x2+…+xn=m(m,n∈N∗)有个非负整数解(x1,x2,…,xn);当m≤n时,有个正整数解(x1,x2,…,xn).基于这一结论的组合计数问题是强基计划校考的常考题型.
例16(复旦大学校考试题)已知m,n∈Z,0≤n≤11,满足22020+32021=12m+n,则n=________.
解析
由22020+32021≡1(mod3),得22020+32021=3x+1(x∈N∗);再由22020+32021≡3(mod4),得3x+1≡3(mod4)⇒3x≡2(mod4)⇒x≡2(mod4)⇒x=4y+2(y∈N∗)⇒22020+32021=3(4y+2)+1=12y+7(y∈N∗)⇒(m,n)=(y,7),故n=7.
点评上面是基于带余除法的余数分析,也可由中国剩余定理进行快捷求解.因为22020+32021≡1(mod3)以及22020+32021≡3(mod4),由(3,4)=1,根据中国剩余定理,得22020+32021≡7(mod12),故n=7.
例17在数列{an}中,a1=1,a2=4,且-an-1an+1=2n-1(n≥2,n∈N∗),求a2020的个位数.
解析
把数列递推关系线性化,再对数列{an}作模10分析即可得解.
先证an≠0(n∈N∗),可加强证明an+1=4an-2an-1,an+1>an>0(n≥2).
由初始条件,得 0<a1<a2<a3,且a3=4a2-2a1.
假设已有ai+1=4ai-2ai-1(i=2,3,…,n),且

由已知递推公式,得
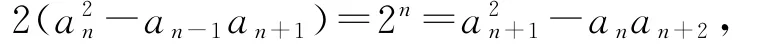

故得ai+1=4ai-2ai-1(i=2,3,…,n+1),且0<a1<a2<…<an<an+1<an+2,所以an+2=4an+1-2an(n∈N∗).
如下取模,找各项个位数字的周期性:{an}(mod10):1,4,4,8,4,0,2,8,8,6,8,0,4,6,6,2,6,0,8,2,2,4,2,0,6,4,4,8,4,0,…,所以从第2项开始呈现周期性,周期T=24;取bn=an+1(n∈N∗),得{bn}是一个周期为T=24的模10数列,故a2020=b2019=b84×24+3≡b3=a4≡8(mod10).
综上,故a2020的个位数是8.
点评
例18凸五边形ABCDE的对角线CE分别与对角线BD,AD交于点F,G,已知BF∶FD=5∶4,AG∶GD=1∶1,CF∶FG∶GE=2∶2∶3,则△CFD,△ABE的面积比S△C F D∶S△A B E=( ).
A.8∶15 B.2∶3
C.11∶23 D.前三个答案都不对
解析
如图4,记S△C F D=s,则S△D F G=s,
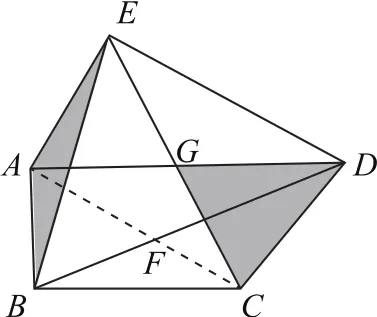
图4
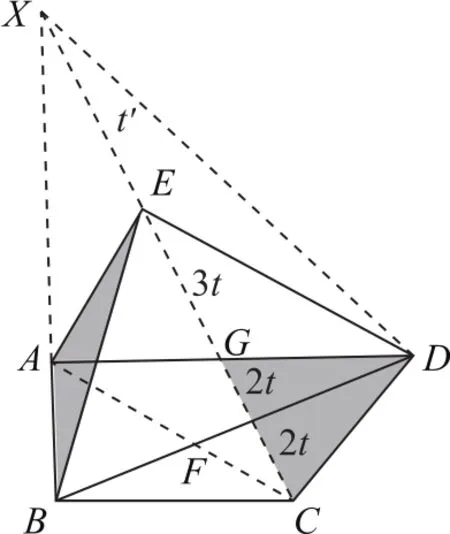
图5
如图5,延长BA交CE于X,记CF=FG=2t,则GE=3t;记EX=t′,由直线BX截△DGF,应用梅涅劳斯定理,得

所以

因为

所以
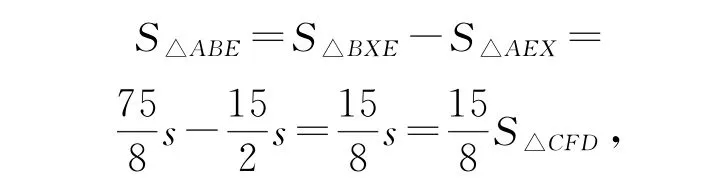
故S△C F D∶S△A B E=8∶15,选 A.
点评
高考已不再出现单纯的平面几何题目,但强基计划校考中注重检测平面几何的推证与计算,从强基计划实施元年试题看,各校注重的是与比例有关的推证与计算,求解也涉及梅涅劳斯定理、塞瓦定理等.
例19(上海交通大学校考试题)函数f(x)=|x2-a|(x∈[-1,1])的最大值记作M(a),则M(a)的最小值是________.
解析
按题意,一方面,有
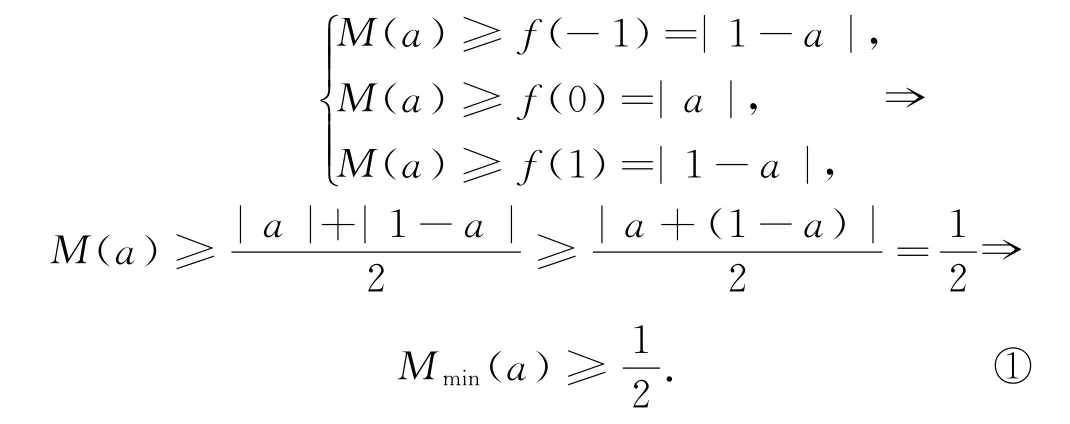
另一方面,取
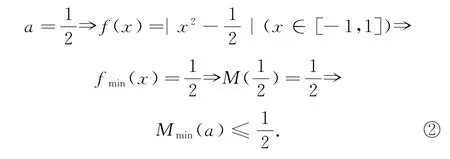
点评
通常解题时会先求出M(a)的表达式,将函数化成单变量函数求最值.这里应用插值法建立最值下界,再用极端性思想探求最值上界,上下界挤夹求得复合最值.复合最值是有挑战性的一类问题,在强基计划校考中属于高频考点.
6 大学先修课程

表6
例20(复旦大学校考试题)已知P为直线
解析
点评
强基计划校考数学试题要求考生掌握低阶行列式展开计算.
例21(北京大学校考试题)若函数f(x)=x5+px+q有有理根,并且正整数p,q≤100,求满足条件的有序数对(p,q)的个数.
解析
由p,q是正整数,所以整系数多项式f(x)无正根,也没有零根,记其有理根,其中(u,v)=1,不妨设v<0,u>0.
情形1v=-1,1+p=q∈{1,2,3,…,100},从而q∈{2,3,…,100},故这样的有序数组(p,q)=(q-1,q)共计99个.
情形2v=-2,2p+32=q≤100,从而p∈{1,2,…,34},故这样的有序数组(p,q)=(p,2p+32)共计34个.
综上,由分类加法原理,易得满足题意的有序数组(p,q)的个数为99+34=133个.
点评
本题虽然是组合计数,但要了解整系数高次方程有理根的判别方法.

