绳子突然拉紧问题的解法探究

◇ 山东 姚桂元

在高考备考过程中，我们经常会遇到绳子突然拉紧的问题．由于作用是在瞬间完成的，绳子的形变不明显，物体的动量变化与能量变化往往不会引起学生的足够重视，从而导致解题出现错误．本文从2019年4月浙江省新高考物理选考13题的解析出发，对教学中经常出现的几例绳子突然拉紧的问题进行分类研究，根据各类问题的特点，总结出解决问题的基本方法，以期对课堂教学提供帮助．

1 绳子一端固定的情形

例1（2019年4月浙江新高考物理选考，13题）用长为1.4m的轻质柔软绝缘细绳，拴一质量为1.0×10－2kg、电荷量为2.0×10－8C的小球，细绳的上端固定于O点．现加一水平向右的匀强电场，平衡时细绳与铅垂线成37°，如图1．现向左拉小球使细绳水平且拉直，静止释放，则（sin37°＝0.6）（ ）．

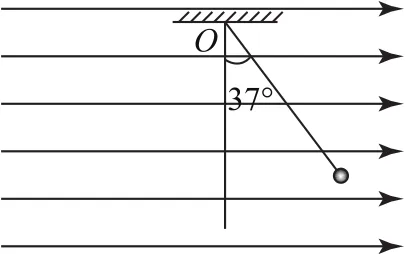
图1

A．该匀强电场的场强为3.75×107N·C－1

B．平衡时细绳的拉力为0.17N

C．经过0.5s，小球的速度大小为6.25m·s－1

D．小球第一次通过O点正下方时，速度为7m·s－1

解析

平衡时，对小球进行受力分析如图2所示，由平衡条件知FTcosθ＝mg，FTsinθ＝q E，解得E＝3.75×106N·C－1，FT＝0.125N，故选项A、B错误．现向左拉小球使细绳水平且拉直，静止释放瞬间，对小球受力分析如图2所示，由牛顿第二定律得，解得a＝12.5m·s－2．

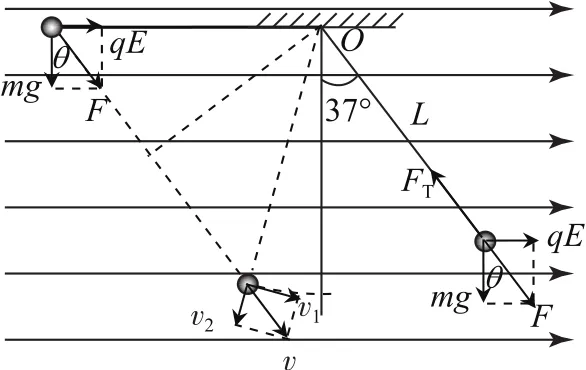
图2

因此，小球沿着与铅垂线成37°角的方向做初速度为零的匀加速直线运动，直到细绳再次被拉直时匀加速直线运动结束．设小球做匀加速直线运动的时间和末速度分别为t、v．由运动学公式可得2Lsinθ＝，得

经过0.5s，小球的速度大小为v′＝at′＝6.25m·s－1，故选项C正确．

在绳子拉紧瞬间，小球沿绳方向的速度v2瞬间变为零，垂直于绳方向的速度v1不变．

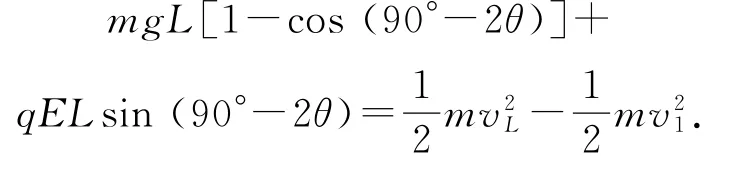
解得vL≈5.8m·s－1，故选项D错误．

【解法总结】在绳子拉紧瞬间，绳子的拉力对小球产生较大的冲量作用．绳子一端固定，沿绳方向的速度在绳子冲量的作用下瞬间变为零，而垂直于绳方向的速度不变．因此，小球的动量发生了变化，能量也发生了变化．

例2（题源追溯）如图3所示，质量为m的小球与一不可伸长的长为L的轻绳连接，绳的另一端固定于O点，现将小球拉到与水平方向成30°角的上方（绳恰伸直），然后将小球自由释放，求小球到达最低点时受到绳的拉力大小．

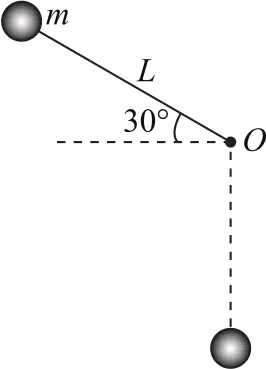
图3

解析

小球自由释放瞬间，对小球受力分析如图4所示．小球只受重力，因此小球释放后先做自由落体运动，当运动到O点斜下方与水平方向成30°角时，绳被拉直，自由落体运动结束．

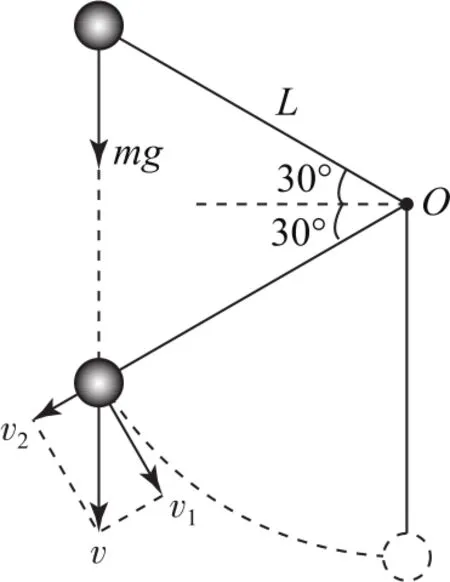
图4

例3（真题改编）用长为1.4m的轻质柔软绝缘细绳，拴一质量为1.0×10－2kg、电荷量为2.0×10－8C的小球，细绳的上端固定于O点．现加一水平向右的匀强电场，电场强度为3.75×106N·C－1，如图5所示．现向左拉小球使细绳水平且拉直，由静止释放，则（ ）．

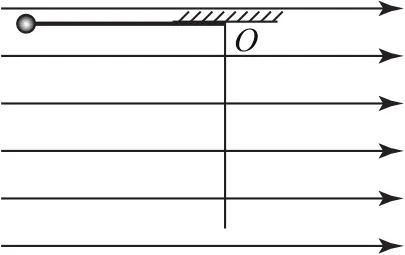
图5

A．小球从释放到运动到最低点的过程中机械能与电势能之和保持不变

B．小球第一次通过O点正下方时，细绳的拉力为0.45N

C．小球先做初速度为零的匀加速直线运动，再做圆周运动

D．经过0.5s，小球的加速度大小为12.5m·s－2

解析

现向左拉小球使细绳水平且拉直，由静止释放的瞬间，对小球受力分析如图6所示，由几何关系得，解得θ＝37°．由牛顿第二定律得，解得a＝12.5m·s－2．

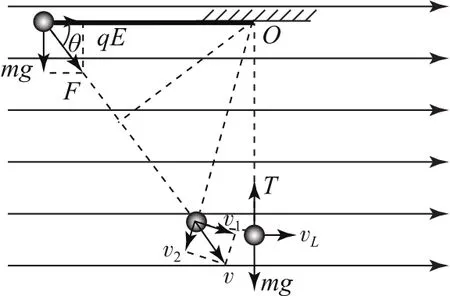
图6

因此，小球沿着与铅垂线成37°角的方向做初速度为零的匀加速直线运动，直到细绳再次被拉直时匀加速直线运动结束．设小球做匀加速直线运动的时间和末速度分别为t、v．由运动学公式得

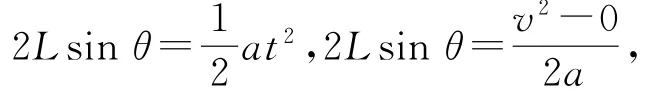
故经过0.5s，小球的加速度大小为12.5m·s－2，故选项D正确．

在绳子拉紧瞬间，小球沿绳方向的速度v2瞬间变为零，垂直于绳方向的速度v1不变．由运动分解可得

由于小球的速度由v突然减小为v1，则绳子拉紧时小球的机械能有损失，因此小球从释放到运动到最低点的过程中机械能与电势能之和变小，故选项A错误．

绳子拉紧之后，小球继续下摆做圆周运动．故小球先做初速度为零的匀加速直线运动，再做圆周运动，选项C正确．

设小球第一次通过O点正下方时，速度大小为vL，由动能定理得mg L[1－cos（90°－2θ）]＋q EL·

2 绳子两端自由的情形

例4如图7所示，可看成质点的质量均为m的两个小球A、B，由长为L的不可伸长的轻绳连接，小球B被限制在水平面上的光滑直槽内，A、B垂直于槽且相距为L/2，若小球A以速度v在光滑桌面上沿平行于槽的方向运动，求小球B开始运动时的速度大小，及此时小球A的速度大小．

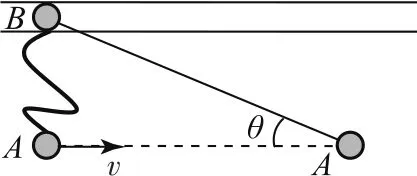
图7

解析

方法1（隔离法） 如图8所示，当轻绳刚拉直时，对小球A，由运动分解得

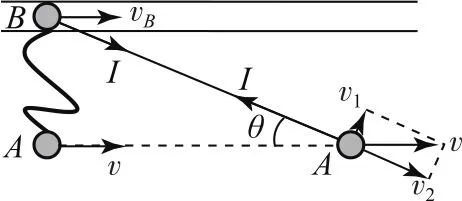
图8

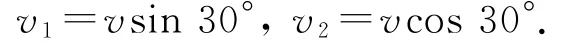
绳子拉紧瞬间，小球A沿绳方向的速度v2变为v′2，垂直于绳方向的速度v1不变．在绳子拉紧过程中，设绳子对小球的冲量为I，由动量定理得

对小球B:Icos30°＝mvB－0，

对小球A:－I＝mv′2－mv2．

绳子不可伸长，沿绳方向速度相等，有v′2＝vBcos30°，解得．故小球A的速度为

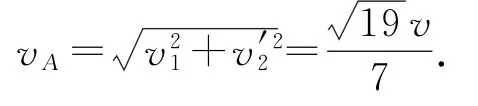
方法2（整体法） 如图8所示，绳子拉紧瞬间，小球A沿绳方向的速度v2变为v′2，垂直于绳方向的速度v1不变．在绳子拉紧的过程中，对A、B组成的系统，沿槽方向，由动量守恒定律得

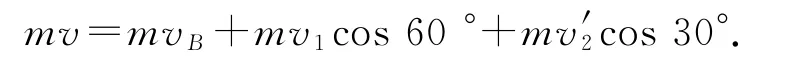
绳子不可伸长，沿绳方向速度相等，有v′2＝vB·cos30°，解得．所以小球A的速度为

【解法总结】在绳子拉紧瞬间，绳子的拉力对两小球产生较大的冲量作用．绳子两端自由，沿绳方向两小球的速度发生变化，而垂直于绳方向的速度不变．因此，两小球的动量发生变化，能量也发生变化．由于绳子不可伸长，故沿绳方向速度相等．若采用整体法，绳子对小球的作用属于内部作用，不用考虑，因此解决此类问题采用整体法会比较简洁．

例5质量分别为mA、mB和mC的三个质点A、B、C位于光滑的水平桌面上，用已拉直的不可伸长的柔软轻绳AB和BC连接，∠ABC为π－α，α为一锐角，如图9所示，今有一冲量为I的冲击力沿BC方向作用于质点C，求质点A开始运动时的速度．

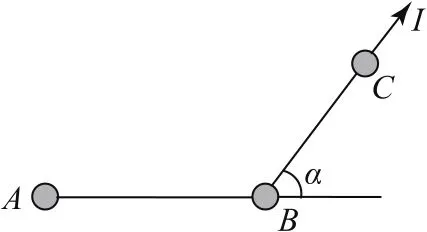
图9

解析

这道题我们采用整体法来解答．建立如图10所示的直角坐标系，设质点A、B、C的速度分别为vA、vB、vC，其中vB与x轴的夹角为θ，以质点A、B、C组成的系统为研究对象．

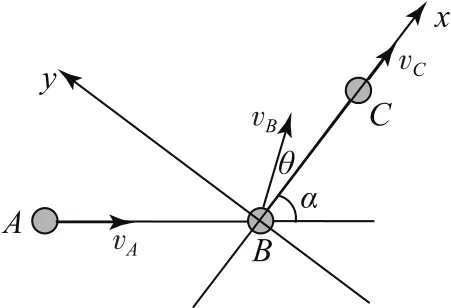
图10

在x方向，由动量定理得

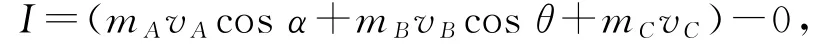
在y方向，由动量守恒定律得

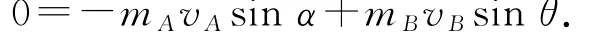
绳子不可伸长，沿绳方向速度相等，有

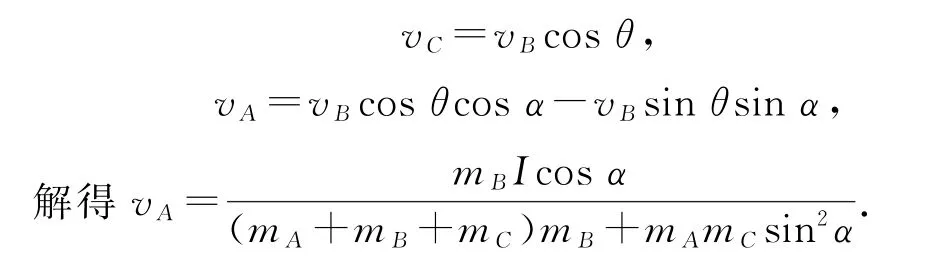
绳子突然拉紧时的问题在全国中学生物理竞赛试题中也经常出现，我们不妨再来研究一道竞赛真题，体会一下解决此类问题的基本方法．

例6（2007年第24届全国中学生物理竞赛决赛试题）A、B、C三个刚性小球静止在光滑水平面上，它们的质量皆为m，用不可伸长的长度皆为l的柔软轻绳相连，AB的延长线与BC的夹角为，如图11所示．在此平面内取正交坐标系x Oy，原点O与B球所在处重合，x轴正方向和y轴正方向如图．另一质量也是m的刚性小球D位于y轴上，沿y轴负方向以速度v0（如图）与B球发生弹性正碰，碰撞时间极短，设刚碰完后，连接A、B、C的连线都立即断了（不计绳断消耗的机械能）．求碰后经过多长时间，D球距A、B、C三球系统的质心最近．

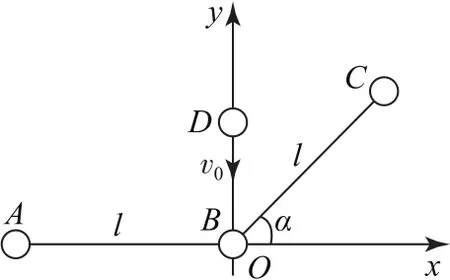
图11

解析碰撞之后各小球的速度如图12所示，对A、B、C、D组成的系统，由动量守恒定律得

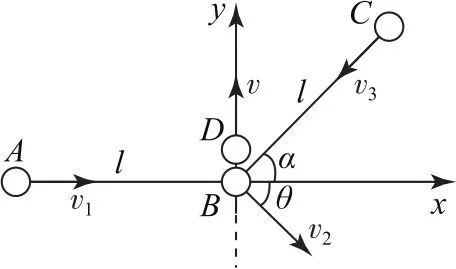
图12

x方向:

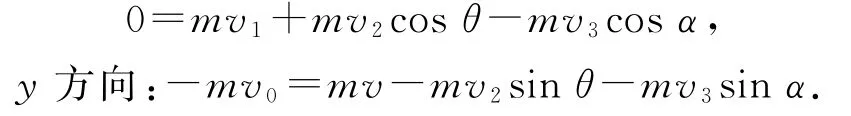
由机械能守恒定律得

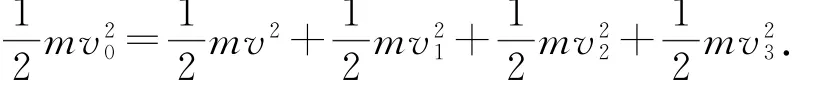
沿绳方向速度相等，有

设碰前A、B、C三球质心位置为（xC，yC），碰后质心速度为（vCx，vCy）．由质心运动方程得

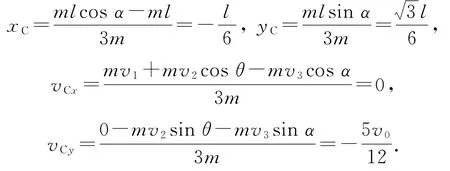
设碰后经过t时间，D球距A、B、C三球系统的质心最近，由几何知识得vt＝yC＋vCyt，解得