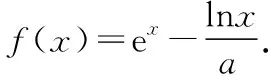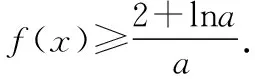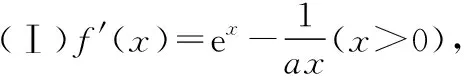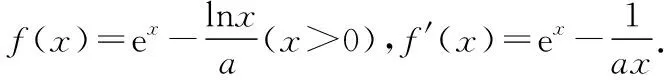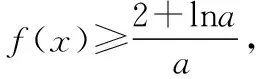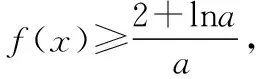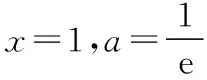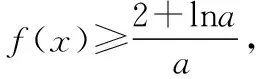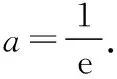函数诚可贵,联系价更高
——以导数中的六个函数为例
宁夏 陈熙春
导数是高中数学的重要内容,同时导数也是研究函数问题的重要工具,在导数的学习中有六个非常重要的函数模型是高考的热点和难点,熟练掌握它们的性质、图象等,对于解决含有指数式、对数式等复合函数的最值、极值、零点个数、求参数范围等问题非常重要,在解题过程中要以这六个函数为基本模型,把复杂的问题通过联想转化为熟悉的基本模型来解决,有利于快速找到解题思路,达到事半功倍的解题效果.
一、导数中的六个重要函数模型
1.六个重要函数模型
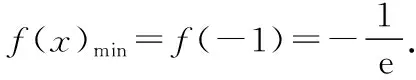
2.六个基本函数的联系
以f(x)=x·ex为母函数的“联系函数”.

(5)y=xlnx=elnxlnx=f(lnx).
可以看出,这六个函数有着密切的联系,根据解题的需要,可以进行相互转化.“根深才能叶茂”,只有熟练掌握它们的联系,才能在解题中灵活运用,下面从五个方面谈谈六个函数在解题中的应用.
二、构造函数判断函数的单调性
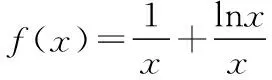
( )
A.(-∞,1) B.(0,1)
C.(0,e) D.(1,+∞)


三、构造函数求参数的取值范围
1.直接利用基本函数
类型1:含有指数式
例2.若函数f(x)=ex-ax2在区间(0,+∞)上有两个极值点x1,x2(0 ( ) 类型2:含有对数式 例3.函数f(x)=xlnx-mx2有两个极值点,则实数m的取值范围是 ( ) C.(0,1) D.(0,+∞) 评析:可以看出,含有指数式和含有对数式的解题思路完全相同.只不过本题还需要联系基本函数进行变形,再进行构造基本函数.教学中要善于把学生从陌生的情境中引到熟悉的情境中,以激发学生的思考. 2.变形两次,构造基本函数 类型1:乘积型aea≥blnb 例4.已知不等式λeλx≥lnx,x∈(e2,+∞),求λ的取值范围. 评析:解法1构造基本函数是以左边的函数为目标,构造函数g(x)=xex,解法2构造基本函数是以右边的函数为目标,构造函数g(x)=xlnx,解法3是两边取自然对数构造基本函数,显然解法3最简单,因为构造出的函数的单调性非常明显,所以在遇到乘积型aea≥blnb时,两边取对数是最有效的方法.以上三种方法都用到了联系的观点,殊途同归,真可谓“千淘万漉虽辛苦,吹尽狂沙始到金”. (Ⅰ)讨论函数f(x)的单调性; (Ⅱ)求证:(ex-1)ln(x+1)>x2. 解析:(Ⅰ)对已知函数求导,得 评析:本题是指对转换构造函数证明不等式问题.从构造方法入手,证法1把x变形为ln(ex-1+1)是解题的重要环节,证法2把x变形为eln(x+1)-1,使不等式左右两边具有相同的结构,运用了整体思维优化解题策略,起到了“山重水复疑无路,柳暗花明又一村”的功效. 类型3:加减型ea±a≥b±lnb 例6.已知函数f(x)=x-ln(x+1),g(x)=ex-x-1.若g(x)≥kf(x)对∀x∈[0,+∞)恒成立,求实数k的取值范围. 解析:由题意得ex-x-1≥k[x-ln(x+1)],右边式子凑1得ex-x-1≥k[x+1-ln(x+1)-1],即ex-x-1≥k[eln(x+1)-ln(x+1)-1],因为x≥0,所以x≥ln(x+1)≥0,构造函数y=ex-x-1.又因为y=ex-x-1在[0,+∞)单调递增,且当x=0时y=0,所以不等式恒成立满足k≤1即可. 评析:运用联系的观点构造函数模型y=ex-x-1是解决此题的关键.从而启发我们在解题过程中要想构造出适合的数学模型,做题必须做到“工夫在诗外”,博观而约取,厚积才能薄发. 1.换元构造基本函数 例7.已知函数f(x)=xex-a(x+lnx)(x>0).讨论函数f(x)的零点个数. 评析:利用换元法构造基本函数,把函数f(x)的零点个数问题转化为基本函数的图象交点个数问题. 2.变形构造基本函数 例8.已知函数f(x)=ex-1-alnx,0≤a≤e,求证:f(x)无零点. 评析:从观察联想入手,通过构造两个基本函数,分别求出它们的最值,问题就迎刃而解了,这样精彩的解法,真是“晴空一鹤排云上,便引诗情到碧霄”. 1.转化为重要函数证明不等式 评析:本题通过简单的变形,就可以转化为基本函数的最值问题. 2.指对分离,构造函数证明不等式 (Ⅰ)求a,b; (Ⅱ)证明:f(x)>1. 由题意可得f(1)=2,f′(1)=e,故a=1,b=2. (Ⅱ)分析:常规方法证明 评析:在要证明的不等式中如果同时含有指数式和对数式,则在证明过程中要进行指、对分离,“改头换面”,把指数式和对数式分别放在不等式的两边,采用“分而治之”的策略,分别求出不等式两边的基本函数的最值. 导函数的零点,根据其数值计算上的差异,可以分为两类:(1)数值上能够精确求解的,称为显零点.(2)能够判断其存在但是无法直接表示的,称为隐零点. 对于隐零点问题,由于涉及灵活的代数变形技巧、抽象缜密的逻辑判断和巧妙的不等式应用,对学生的综合能力要求比较高,是导数综合问题中的一个难点. (Ⅰ)若f(x)在[1,2]上是减函数,求实数a的最大值; (Ⅱ)证法1:常规解法(虚设零点——隐零点代换) 证法2:构造函数法,分而治之 证法3:构造函数法 又g(lnx)=elnx-lnx-1=x-lnx-1≥0,② 证法4:指、对放缩法 利用上面的方法可以顺利地解决2015年全国卷Ⅰ文科第21题节选,请读者尝试. 评析:(1)隐性零点代换实际上是一种“明修栈道,暗度陈仓”的策略,也是数学中“设而不求”思想的体现.导函数零点虽然隐形,但只要抓住其特征(零点方程),判断其范围,最后整体代入即可. (2)对两个重要不等式ex≥x+1,x-1≥lnx的应用要高度重视,如证法4巧妙地运用这两个重要不等式进行连续放缩证明,使解题过程简洁,运算速度快,正确率高. (3)“秀枝一株,嫁接成林”,四种证明方法各有千秋,分别从不同的视角切入,真是“横看成岭侧成峰,远近高低各不同”,体现了思维的灵活性.





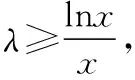
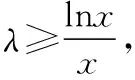




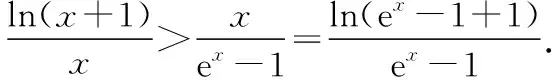


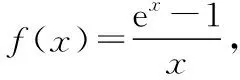
四、构造函数判断零点个数



五、构造函数证明不等式

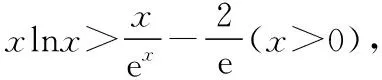







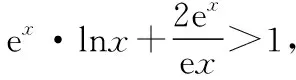

六、导数的隐零点问题