横看成岭侧成峰，远近高低各不同——2020年新高考Ⅰ卷(供山东省使用)第20题的解法探讨

山东 李 斌 耿晓红

2020年新高考数学试题在命制的过程中重视难度和思维的层次性，给广大学生提供更广阔的思考空间，更多的思考角度，以及基于自己认知水平的发现和探索解题方法的不同平台.例如第20题具有多种解法，体现了解题方法的多样性，给不同层次的考生提供了多种分析问题和解决问题的途径.

一、试题再现

(2020·新高考Ⅰ卷(供山东省使用)·20)如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.

(Ⅰ)证明：l⊥平面PDC；

(Ⅱ)已知PD=AD=1,Q为l上的点，求PB与平面QCD所成角的正弦值的最大值.

【分析】该题考查的是有关立体几何的问题，涉及的知识点有线面平行的判定和性质，线面垂直的判定和性质，利用空间向量求线面角，利用基本不等式求最值，属于中档题目.第一问就难倒不少学生，找不到交线l在哪里，不能将l⊥平面PDC转化成其他直线垂直于平面PDC，当然也就无从证明,得分率较低.第二问失分点一是点Q的坐标不会设，找不到合理的变量，无法表示线面角的正弦值；失分点二是建立函数关系后，不会合理求最值，下面我们一起来看看该题在不同视角下的解法探究.

二、解法探究

1.第一问之探究视角

视角一：利用线面平行性质定理找l的平行线

解法一：∵PD⊥底面ABCD，∴PD⊥AD.∵底面ABCD是正方形，∴AD⊥DC，又PD∩DC=D,∴AD⊥平面PDC.

∵AD∥BC,AD⊄平面PBC,BC⊂平面PBC,∴AD∥平面PBC.

∵平面PAD∩平面PBC=l,AD⊂平面PAD,∴l∥AD.∴l⊥平面PDC.

【评析】该解法为常规证明，构造线面平行的条件，证明l∥AD.

视角二：利用面面平行性质定理找l的平行线

解法二：思路1：过A作AG∥BP，∵AD∥BC，∴平面ADG∥平面BCP，∵平面PAD分别交平面ADG和平面PBC于AD和l，∴l∥AD.

∵PD⊥底面ABCD，∴PD⊥AD.∵底面ABCD是正方形，∴AD⊥DC，又PD∩DC=D,∴AD⊥平面PDC.∴l⊥平面PDC.

思路2：分别取AB，DC，PD，PA的中点E，F，G，H，易证得平面EFGH∥平面PBC.平面PAD分别交平面EFGH和平面PBC于GH和l，∴l∥GH.∵GH∥AD,∴AD∥l.

∵PD⊥底面ABCD，∴PD⊥AD.∵底面ABCD是正方形，∴AD⊥DC，又PD∩DC=D,∴AD⊥平面PDC.∴l⊥平面PDC.

【评析】构造两个平行平面，与第三个平面PAD相交，得到AD∥l，利用的是面面平行性质定理.

视角三：补空间几何体找交线l

解法三：思路1：∵四棱锥P-ABCD的底面是正方形，PD⊥底面ABCD,

∴DP，DA，DC两两垂直，以DP，DA，DC为三条棱作长方体ABCD-EFGP.

∴EP∥AD∥BC，∴EP⊂平面PAD,EP⊂平面PBC，EP就是l.

因为在长方体中，所以l⊥平面PDC.

思路2：∵四棱锥P-ABCD的底面是正方形，PD⊥底面ABCD，

∴DP，DA，DC两两垂直，作AE∥DP，PE∥AD，AE∩EP=E，以PE，DA，BC为棱作直三棱柱ABE-DCP.

∴EP∥AD∥BC，∴EP⊂平面PAD,EP⊂平面PBC，EP就是l.

∵在直三棱柱中，∴l⊥平面PDC.

【评析】交线l在原图中没有显现出来，我们可以通过构造长方体或直三棱柱，利用几何体的结构特征,将交线在几何体中表现出来，进而更容易判断.

视角四：利用线线平行作交线l

解法四：∵PD⊥底面ABCD，∴PD⊥AD.∵底面ABCD是正方形，∴AD⊥DC，又PD∩DC=D,∴AD⊥平面PDC.

思路1：过P作PE∥AD，∵AD∥BC，∴PE∥BC，∴PE就是l.∴l⊥平面PDC.

思路2：过A作AE∥DP，且AE=DP，则四边形ADPE是平行四边形，∴AD∥EP.∵AD∥BC，∴EP∥BC，∴PE就是l.∴l⊥平面PDC.

思路3：过A作AE⊥平面ABCD且AE=DP，∵PD⊥底面ABCD，∴AE∥DP，则四边形ADPE是平行四边形，∴AD∥EP.∵AD∥BC，∴EP∥BC，∴PE就是l.∴l⊥平面PDC.

【评析】通过视角四，或构造平行四边形证明线线平行，也是几何证明中的常见方法.

视角五：利用线面垂直的关系找与l垂直的相交直线

解法五：∵PD⊥底面ABCD，BC⊂平面ABCD，∴PD⊥BC.

∵底面ABCD是正方形，∴BC⊥DC，

又PD∩DC=D,∴BC⊥平面PCD.

过D作DN⊥PC，垂足为N，DN⊂平面PDC,∴BC⊥DN，

PC∩BC=C,PC,BC⊂平面PBC,∴DN⊥平面PBC,∵l⊂平面PBC，∴DN⊥l.

∵PD⊥底面ABCD，DC⊂平面ABCD，∴PD⊥DC.

∵底面ABCD是正方形，∴AD⊥DC.

∵AD∩PD=D,AD,PD⊂平面PAD,∴DC⊥平面PAD.∵l⊂平面PAD,∴DC⊥l.

∵DC∩DN=D,DC,DN⊂平面PDC,∴l⊥平面PDC.

【评析】直接在平面PDC内找两条与l垂直的相交直线，利用线面垂直的判定定理证明.

视角六：利用面面垂直关系找交线l

解法六：∵PD⊥底面ABCD，AD⊂平面ABCD，∴PD⊥AD.

∵底面ABCD是正方形，∴AD⊥DC，

又PD∩DC=D,∴AD⊥平面PDC,∵AD⊂平面PAD，∴平面PAD⊥平面PDC.

∵PD⊥底面ABCD，BC⊂平面ABCD，∴PD⊥BC.

∵底面ABCD是正方形，∴BC⊥DC，

又PD∩DC=D,∴BC⊥平面PDC,∵BC⊂平面PBC，∴平面PBC⊥平面PDC.

∵平面PBC∩平面PAD=l.∴l⊥平面PDC.

【评析】若垂直于同一平面的两个平面相交，则交线也垂直于该平面.因为平面PBC∩平面PAD=l，只需证明平面PAD⊥平面PDC，平面PBC⊥平面PDC即可.

视角七：利用坐标法证明线面垂直

解法七：分别以DA，DC，DP所在直线为x轴、y轴、z轴建立如图所示的空间直角坐标系.

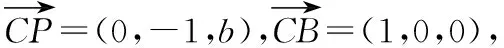
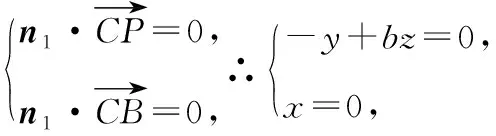
平面PAD的一个法向量是n2=(0,1,0),

【评析】根据视角七，求出平面PBC和平面PAD的法向量，再求交线l的方向向量，与平面PAD的法向量平行即可.

2.第二问之探究视角

问题1：如何找到PB与平面QCD所成角？

视角一：几何法

解法一：设PQ=a，连接QC，QD,QC∩PB=O，作PH⊥QD,垂足为H，连接OH.∵CD⊥平面PAD,∴CD⊥PH，∵CD∩QD=D,CD,QD⊂平面QCD，∴PH⊥平面QCD，所以∠POH就是直线PB与平面QCD所成角，

【评析】利用线面角的定义，找到PB在平面QCD内的射影OH，即可找到线面角∠POH，解直角三角形POH就行.

视角二：坐标法

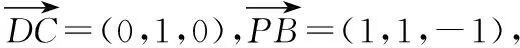
【评析】建立空间直角坐标系，利用空间向量求角的正弦值，是最为常见的解题方法.

问题2：如何求PB与平面QCD所成角的正弦值的最值？

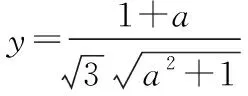
视角一：重要不等式法

视角二：基本不等式法

当且仅当a=1时等号成立.

视角三：换元法

设1+a=t，

视角四：导数法

当00，y是增函数，当a>1时，y′<0，y是减函数，

视角五：判别式法

∴(3y2-1)a2-2a+3y2-1=0有实数解，

【评析】近几年，立体几何中动态问题一度成为热点内容，其中和函数模型有关的最值问题大多为二次函数、分式函数、三次多项式函数的最值，所以熟练掌握一些常见函数模型的最值问题的求解方法是十分必要的.

三、教学思考

1.立体几何问题在形成空间观念、培养空间想象能力和巩固逻辑思维能力方面有着独特的作用，在几何体中找到图形的特征，找到几何元素间的关系，建立未知量与已知量间的关系进行证明.

2.对于一道数学题，由于着眼点和角度的不同，会有许多不同的解题方法，对已解决的典型题目，应指导学生再回首从多角度、多方位去思考，寻求更简捷巧妙的解法，反思解题的规律，发现知识间的联系，挖掘数学思想与方法，提升数学核心素养和解题能力.