结合2020年新高考Ⅰ卷(供山东省使用)高考试题——浅谈对一题多选试题的几点思考

江苏 张路民

期盼已久的2020年高考已悄然结束，作为第二批启动新高考的省份，山东和海南的高考试题备受关注.之前一直盛传的“一题多选”终于得到验证，为之后参加新高考改革省份的数学教学明确了方向.这也是几十年高考以来的一次重大突破.“一题多选”这样设置的数学题有考试分值小、考查容量大、解题思路广、蕴含数学思想丰富、对学生多层次考查、区分度大等特点，更容易考查学生的基础知识以及综合能力，使数学在高考中的选拔作用更为突出.当然对于广大考生包括教师来说都是一项全新的课题，需要进一步研究与开发.下面笔者结合2020年新高考Ⅰ卷(供山东省使用)谈谈对“一题多选”试题的理解及思考.

首先来回顾一下这次山东的多选试题：

四道多选试题分别考查了圆锥曲线、三角函数、不等式和概率与统计，知识点基本较分散，有几何，有代数，有概念辨析也有纯计算验证.试题难度相对适中，有梯度.进一步思考能发现试题其实也渗透着许多细节，值得推敲与研究，便于在后续的教学中有所帮助.

1.多选题的引入增加了学生的答题时间

如果是单选题，那么只要确定一个满足题意的选项就行，即使原来江苏卷的纯填空题也只要能做出答案就行.但是对于多选题，每一个选项都可能是满足题意的，所以需要逐一地计算审核，这无疑增加了学生的答题时间.

( )

A.若n=1，则H(X)=0

B.若n=2，则H(X)随着p1的增大而增大

D.若n=2m，随机变量Y所有可能的取值为1,2,…,m，且P(Y=j)=pj+p2m+1-j(j=1,2,…,m)，则H(X)≤H(Y)

【答案】AC.

【点评】这里的四个选项每一个都要进行计算验证.其中选项A,C比较容易验证，这两个选项只要能理解题意，计算量相对较小.但对于选项B,D而言难度就提升了不少，对于选项B:H(X)=-[p1log2p1+(1-p1)log2(1-p1)]，接下来的处理是个难点,多数学生较难联想到通过导数来解决.对于选项D要更加复杂了，相当于以前江苏卷中填空题的压轴题，需要一定的思维和运算功底.H(X)=-(p1log2p1+…+p2mlog2p2m),H(Y)=-[(p1+p2m)log2(p1+p2m)+…+(pm+pm+1)log2(pm+pm+1)],找到两者的联系与作差化简都是难点.纵观本题(其他几题也有类似的情况)可以看出多选题要想完全做好所花的时间是远远多于以前的单选题和填空题的.

2.考查容量大，知识点掌握要全面

多选题的第二个特点是对知识考查的容量较大、知识面广，学生在平时的学习过程中对概念定义要理解透彻.

【例2】(2020·新高考Ⅰ卷(供山东省使用)·9)已知曲线C:mx2+ny2=1.

( )

A.若m>n>0，则C是椭圆，其焦点在y轴上

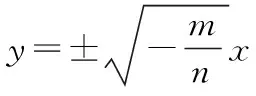
D.若m=0，n>0，则C是两条直线

【答案】ACD.

【点评】这道题本身难度不大，但需要学生对圆锥曲线的方程形式非常熟悉，否则很容易漏选或者错选.在新授课的教学中相信所有教师都是重点强调且不断地进行对比巩固的，因此，在今后的教学中，类似此类的概念辨析需要更加重视.

3.解题思路广、蕴含数学思想丰富

在多选题的题型中，一题多解必然也是出题者会涉及的类型，这就需要学生解题思路要广，理解数学本质，充分运用好所掌握的数学思想方法，能够触类旁通，举一反三.

【例3】(2020·新高考Ⅰ卷(供山东省使用)·10)如图是函数y=sin(ωx+φ)的部分图像，则sin(ωx+φ)=

( )

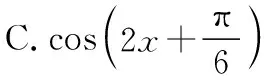
【答案】BC.

【点评】这道题难度也不大.需要学生从两个角度，即根据题设看成正弦函数图象和突破条件所限看成余弦函数图象，就很容易找到答案，而且这道题漏选的可能性较小，就相当于做两道填空题，因此在后期的教学中也需要提醒学生将此类多选题直接看成填空题进行处理，基础好点的学生算出一个答案利用诱导公式也能较轻易地获得另一个答案，能够提高解题效率.

4.考查点细致，关注相关数学结论

在整个高中数学学习过程中有许多细节和数学结论需要学生关注，部分学生只注重解题不重视细节，对课本基础知识不够重视，这对于解决数学多选题将会产生一定的影响.

【例4】(2020·新高考Ⅰ卷(供山东省使用)·11)已知a>0，b>0，且a+b=1，则

( )

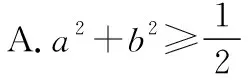
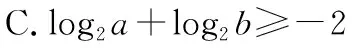
【答案】ABD.

【几点思考】

今年的山东高考卷已经基本为新高考试题定下了基调：“一题多选”试题已经正式进入高考的舞台.这对考生、教师甚至是命题专家而言都是一个全新的挑战，如何能在高考中让多选题少丢分甚至不丢分，今后必将会引起广大数学教育工作者们的积极探讨与研究.由于目前可参考的样本还比较少，笔者在此只能就自己的理解谈几点思考：

1.一题多选会考查哪些知识点？

哪些知识点更容易出现在一题多选中？目前来看很难有一个定论，结合今年的山东高考卷及几次模拟卷笔者觉得至少有以下几个特点：(1)作为高考题为了考查知识点的全面性，多选题跟前面的单选题考查的知识点不重合.(2)基本上会将代数与几何题相结合.(3)代数部分相对而言函数，尤其三角函数、数列、不等式、向量考查的可能性更大，几何部分圆锥曲线的定义与性质、立体几何的线面关系、距离角度和体积等都较容易命制一题多选.另外我们前面比较淡化的概率与统计等也会在一题多选中占据一席之位.当然单纯从出题角度来讲任何章节都可以有多选题，但考虑到试卷的整体性及实际考查的需要，以上内容考查到的可能性会更加突出一些.

2.一题多选的形式会有哪些？

多选题不是把单选简单变为多选，更不是对现有的单选题直接进行否定而得到.多选题应该是同一情境下多个结论的判断，而不是把一些知识点凑在一起、把几个不相关的真命题和假命题放在一起类似拼盘式的大杂烩.这四个选项到底如何设置，以什么形式出现，也将会是出题者们需要研究的课题.其实在2019年全国卷Ⅰ第11题和全国卷Ⅲ第12题均出现了组合型选择题，这应该也是为了接轨新高考的一题多选.当时给出的题基本都是我们平常较熟悉的一个题设下的多个结论.结合今年的高考试题以及参考其他学科，笔者总结了以下几个数学多选题的命制类型：

(3)同条件多结论.如，设等差数列{an}的前n项和为Sn，公差为d，且满足a1>0，S11=S18，则对Sn描述正确的有( )A.S14是唯一最大值；B.S15是最大值；C.S29=0；D.S1是最小值.一个问题产生多个结论应该在多选题中占据比较大的比重，这类题要求考生对知识的掌握要全面，理解要到位.

(4)一个条件下的结论，以不同的形式出现.如2020年新高考Ⅰ卷(供山东省使用)的第10题，用不同的形式去表示同一个结论，这类选项相对要容易一些，因为选项之间有一定的关联.

(5)条件提供信息，结论需要探索延伸.这种类型一般会作为该题型的压轴题，其中个别选项会稍有难度，以达到一定的区分度.如2020年新高考Ⅰ卷(供山东省使用)的第12题.

3.一题多选的难度到底会怎样？

多选题的得分肯定会比单选题的得分要困难一些，为了平衡由于多选带来的难度，所以在选项上势必会降低难度，这一点在今年的高考试题中已经得到验证，仔细研究每一个选项，尤其是前三题，基本没有特别难以判断的，比以前单选题的最后几题难度要稍简单一些.更重视对基础知识和基本方法的考查.当然个别题肯定还是会设置一定的难度，但对于基础较好，学习能力较强的考生来讲难度还是比较适中的.

4.一题多选题有没有解题技巧？

多选题型的解题技巧需要在平常的学习过程中不断总结反思，学无定法，贵在得法.要想在高考中确保多选题少丢分，笔者认为需要注意以下几点：

(1)务必要夯实基础.多选题型虽然是新高考背景下命题形式上的创新，但此类题型对中学数学主干知识的考查不变，中学数学传统意义上的主干知识是构筑中学数学这座大厦的根基，无论高考改革到什么程度，这些主干知识的考查一定不会冷落.因此，在日常的教学中，教师务必要更加重视夯实基础和对概念教学的精准把握,让学生知其然还要知其所以然.

(2)要善于挖掘数学问题的本质.数学本质就是体现和渗透在问题中的知识、方法、规律及数学思想方法乃至数学核心素养，将本质性的东西深刻挖掘了、弄熟吃透了，即使是呈现在大家面前的新问题，可能就是在原问题基础上进行某种程度的改头换面，只要能看透变式后的本质，那么问题无论如何变，解决起来都会游刃有余了.

(3)要学会取舍,善于对比.在解决多选题的过程中对每个选项要仔细斟酌,善于比较,对于部分选项也可以采用单选题的解题策略，如,特殊值法、排除法等,像2020年新高考Ⅰ卷(供山东省使用)的第10题就可以根据周期排除选项A,再比较选项C,D可以得出二选一,基本结合选项B就能得到答案.

(4)要善于利用得分规则.题目规则是有选错的得0分,部分选对的得3分,这一点很重要,一旦出现拿捏不准的选项,还是要采用保守策略,选自己最有把握的选项,选择一个即可,以免扣分.当然能解决的题尤其是前三题还是需要尽量选完整,少丢分的前提还是尽量不丢分.