学会归类与整理,突破函数不等式

甘肃 张建文

函数类不等式的证明是导数压轴题中非常重要的一类不等式,这类不等式在高考题和模拟题中是经常见到的.不同于其他类型的不等式,函数类不等式的证明基本上是通过对不等式进行等价变形、构造相应的函数、求解函数最值来实现的.不等式的变形与函数构造因不等式结构的不同而有所区别.本文通过研究函数类不等式的组成元素和处理方法，归纳整理知识之间的逻辑关系,得到证明函数类不等式的通性通法.下面笔者就不同类型的函数类不等式的变形方法和函数构造原则进行简单论述.

一、常见函数类不等式证明方法

1.直接法求解函数最值

当x∈I时,证明:不等式f(x)≥g(x)成立.

思路1:f(x)≥g(x)⟺f(x)-g(x)≥0,令h(x)=f(x)-g(x),只需求出x∈I时,hmin或h(x)的下确界即可.

思路2:f(x)≥g(x)⟺g(x)-f(x)≤0,令h(x)=g(x)-f(x),只需求出x∈I时,hmax或h(x)的上确界即可.

2.寻找充分条件,确定中间参考值

当x∈I时,证明:不等式f(x)≥g(x)成立.

不等式f(x)≥g(x)成立的一个充分不必要条件是f(x)min≥g(x)max,进而构造函数y=f(x)和y=g(x).求解y=f(x)的最小值或下界,y=g(x)的最大值或上界.这种证明方法只适用于某一类特殊不等式,一般需要我们计算出两函数对应的最值.

3.放缩法

放缩法是证明不等式的一种重要的手段，因其思维量大，构造性强，需要有较高的放缩技巧，能够全面综合地考查学生的学习能力，因而经常成为高考压轴题的命题素材.这类问题的解决通常是通过多角度观察式子结构,深入剖析其中的特征,抓住其规律进行恰当地放缩,从而使问题得以解决.

4.分析综合法

分析法的思路是逆向思维,用分析法证明必须从结论出发,倒着分析,寻找命题成立的充分条件.应用分析法证明问题时要严格按照分析法的语言表述,下一步是上一步的充分条件.用综合法证明时,必须首先找到正确的出发点,多角度联想已知条件,层层推进,从而由已知推出结论.分析综合法是分析法和综合法的结合,证明思路一般是运用分析法对结论进行推导,找到成立的充分条件,再利用综合法从已知条件出发推出此条件成立,从而命题得以证明.

二、特殊不等式化简原则

1.只含有lnx的不等式化简原则

若不等式f(x)≥g(x)中只含有xlnx和x的整式表达式,此时我们首先考虑直接法构造函数求解,若无法求解则转而要考虑f(x)≥g(x)的结构特点,比如有xlnx时考虑将lnx与x分离进行思考,这样可以在导函数中避免出现lnx,简化运算过程.

2.只含有ex的不等式化简原则

不等式f(x)≥g(x)中只含有ex和x的整式表达式.对于这类不等式,通常对不等式进行等价变形,构造恰当的函数来求解最值.等价变形是按照简化运算的原则进行:

①尝试构造函数h(x)=f(x)-g(x),求解h(x)的最小值或下界;

②若①无法实现,则考虑将ex与其他表达式整合,变形为exh(x)≥1或exh(x)≤1,构造函数y=exh(x),求解相应的最值或边界值.

3.同时含有ex和lnx的不等式化简原则

若不等式f(x)≥g(x)中含有lnx与ex,通常需要将lnx与ex分离在不等号的两侧,再观察不等式的特点,必要的时候需要在不等式的两边同除以或乘以x进行变形,最后构造函数求解最值证明.

三、典例赏析

1.直接法证明函数类不等式

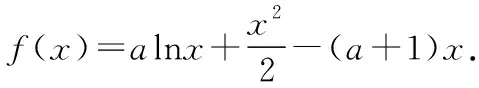
(1)当a>0时,求函数f(x)的单调区间;

解析:(1)当01时，f(x)在(0，1)，(a,+∞)上单调递增，在(1，a)上单调递减.

所以当x∈(0,1)时,f′(x)<0,f(x)单调递减;当x∈(1,+∞)时,f′(x)>0,f(x)单调递增.

点评:直接法是易于理解、便于操作的证明方法,对于难度不大的证明题通常选用这种方法证明.此题只需判断清楚函数单调性就能求出最值,证明结论.在解答完成后需要教师引导学生进行归类总结,获得通性通法.

2.寻找充分条件,确定中间参考值

【例2】已知函数f(x)=1-lnx+a2x2-ax(a∈R).

(1)讨论函数f(x)的单调性；

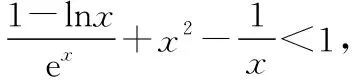
当x∈(0,1)时,令g(x)=x(1-lnx),下面求解g(x)的最大值或上界.

由g′(x)=-lnx>0,g(x)在(0,1)上单调递增,所以g(x)

令h(x)=(1+x-x3)ex,下面求解h(x)的最小值或下界.

h′(x)=(2+x-3x2-x3)ex,令p(x)=2+x-3x2-x3,则p′(x)=1-6x-3x2.

由于y=p′(x)在(0,1)上单调递减,p′(0)=1,且p′(1)=-8,所以p′(x)有一个零点,记为x0.

当x∈(0,x0)时,p′(x)>0,p(x)单调递增；当x∈(x0,1)时,p′(x)<0,p(x)单调递减.

当x∈(0,x0)时,p(x0)>p(0)=2,当x∈(x0,1)时,p(x0)p(1)<0.所以p(x)在x∈(x0,1)存在唯一零点,记为x1.

当x∈(0,x1)时,p(x)>0,h′(x)>0,h(x)单调递增;当x∈(x1,1)时,p(x)<0,h′(x)<0,h(x)单调递减.所以h(x)>min{h(0),h(1)}=min{1,e}=1.

故而(1+x-x3)ex>1,x(1-lnx)<1,即x(1-lnx)<(1+x-x3)ex,原式成立.

点评:此题的证明思路在于将lnx与ex分离在不等号的两侧,运用分析法寻找不等式成立的充分条件，构造两个函数分别求取最值.此题对学生的观察能力要求极高,不仅需要敏锐地观察出式子的结构特点,对不等式进行恰当变形,而且还需要构造双函数解答.

3.放缩法证明不等式

(1)求曲线y=f(x)在点(0,-1)处的切线方程;

(2)证明:当a≥1时,f(x)+e≥0.

解析:(1)2x-y-1=0.

令g(x)=x2+x-1+ex+1,g′(x)=2x+1+ex+1,显然g′(x)在R上单调递增,且g′(-1)=0.

当x∈(-∞,-1)时,g′(x)<0,g(x)单调递减;当x∈(-1,+∞)时,g′(x)>0,g(x)单调递增.

所以当x=-1时,gmin=g(-1)=0,即g(x)≥0,所以f(x)+e≥0，原式得证.

点评:此题利用放缩法对不等式进行放缩,将不等式中的a处理掉,转化为不含参数的不等式,再通过构造函数求解最值进行解答.能否应用放缩法关键要看不等式的结构是否满足放缩条件,教师要引导学生多角度多层次观察,从最常规的解法开始思考,尝试各种可能性,寻求满足本题目的最优解法.

4.分析综合法

【例4】已知函数f(x)=xlnx,g(x)=-x2+mx-2.

(1)若函数y=f(x)-g(x)有且仅有一个零点,求实数m的值;

(2)已知函数h(x)=f(x)-kx2-x,a,b为h(x)的两个极值点(ae2.

解析:(1)m=3.

(2)h(x)=xlnx-kx2-x,x∈(0,+∞),h′(x)=lnx-2kx.由于a,b为h(x)的两个极值点,

所以有F(a)=F(b),0

点评:此题属于极值点偏移问题,需要对结论按照分析法寻找成立的充分条件.此题不仅仅对结论进行等价变形,而且还利用函数单调性进行化简.在构造G(x)后求导过程需要用复合函数的求导法则,先求导后代入,这样可以极大地简化运算过程.

5.只含有lnx的不等式

【例5】已知f(x)=x(lnx+ax+1)-ax+1.

(1)若f(x)在[1,+∞)上是减函数,求实数a的取值范围;

(2)若实数a=-2,证明:f(x)的最大值为2.

解析:(1)a≤-2.

(2)当a=-2时,f(x)=x(lnx-2x+1)+2x+1,欲证f(x)的最大值为2,

当x∈(0,1)时,g′(x)>0,g(x)单调递增;当x∈(1,+∞)时,g′(x)<0,g(x)单调递减.

所以当x=1时,g(x)max=g(1)=0,即g(x)≤0,原式成立.

点评:此题的证明关键在于对不等式xlnx-2x2+3x-1≤0的处理,不等式含有xlnx,需要出现单独的lnx,这样能极大地简化运算过程.若是直接构造函数y=xlnx-2x2+3x-1,最大值的求解是相当烦琐的,对于绝大多数学生来说是求不出来的.因此教师要引导学生观察式子结构,构造恰当的函数进行运算.

6.只含有ex的不等式

【例6】(2018·全国卷Ⅱ理·21)已知函数f(x)=ex-ax2.

(1)若a=1,证明:当x≥0时,f(x)≥1;

(2)若f(x)在(0,+∞)只有一个零点,求a.

当x=0时,g(x)max=g(0)=1,即g(x)≤1.原式得证.

【例7】已知函数f(x)=ex-x2+x-1，x∈[0,+∞).证明:f(x)≥0.

当x∈[0,1)和(2,+∞)时,g′(x)<0,g(x)单调递减;当x∈(1,2)时,g′(x)>0,g(x)单调递增.

所以g(x)max=max{g(0),g(2)}=g(0)=1,即g(x)≤1.原式得证.

点评:例6和例7中的不等式都含有ex和x的整式表达式,按照思路2进行变形.数学解答的思路通常“看”出来的,教师要引导学生学会观察,教会学生“看”的方法.例7中的函数最大值求解需要借助于函数的简单图象,在训练推理论证能力的同时可以培养学生的直观想象素养.

7.同时含有ex和lnx的不等式

(1)讨论函数f(x)的单调性;

当x∈(0,1)时,h′(x)<0,h(x)单调递减;当x∈(1,+∞)时,h′(x)>0,h(x)单调递增.

所以当x=1时,h(x)min=h(1)=e,即h(x)≥e,当且仅当x=1时,等号成立.

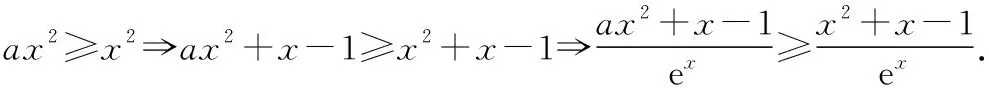
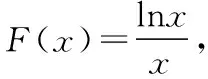
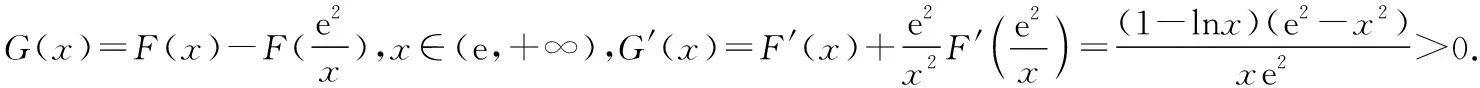
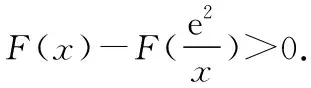
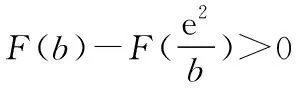
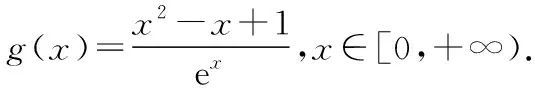
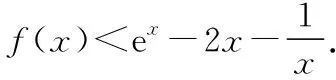
四、总结与展望