改进惯性权重的粒子群优化算法

樊伟萍 李秦

（兰州交通大学数理学院，甘肃 兰州 730070）

1 引言

粒子群优化算法（PSO）是由Kennedy和Eberhart于1995年通过观察鸟群寻找栖息地的行为而简化出的群体智能优化算法［1］，具有设置参数少、易于实现、收敛速度快等优点而备受学者的青睐，但是PSO算法易陷入局部最优值.为了改善这一问题，学者们先后提出了各种应对策略，张迅等［2］人根据高斯函数分布特征设置惯性权重变化策略，文献［3］基于文献［2］提出了惯性权重对数递减的粒子群算法，并引入对数调整因子α ，有助于粒子跳出局部极值，提高了算法的全局收敛性.Clerc 提出了带有收缩因子的PSO算法［4］，整体上具有比标准PSO算法更加高效地收敛性能，但在算法后期的精度比标准PSO算法性能差.总结来说，针对粒子群算法的改进大体上分为参数设置的改进［5-9］和算法融合改进［10-13］，这些策略一定程度上优化了算法性能，提高了PSO 算法的寻优效率，但时间和空间消耗比较高，且无法避免粒子易陷入局部最优，易早熟的问题.本文在Shi和Eberhart提出的粒子群优化算法［2］惯性权重线性递减的基础上，添加了随迭代次数线性递增的调节因子p，使算法在局部搜索能力和全局搜索能力之间得到更好的平衡，同时针对粒子群算法搜索后期易陷入局部最优，影响算法优化性能的问题，在每次迭代时，对种群中的粒子进行突变操作，从而增强粒子跳出局部最优的能力，最后对测试函数进行寻优操作来验证改进后粒子群优化算法（XWPSO）的有效性.

2 粒子群算法

粒子群算法的主要思想是将需要寻优的问题的解想象成一只鸟，称为一个“粒子”，然后让所有粒子在D 维的搜索空间进行搜索，粒子位置的好坏由定义的适应度函数评价，并且给每个粒子赋予记忆功能，能够记忆粒子搜索过程中寻到的最佳位置，同时，各个粒子之间也可以进行信息共享，通过粒子自身经验和同伴的经验来动态调整粒子位置.

粒子群算法中，粒子之间是相互合作，信息互通的，速度更新公式（1）由三部分组成，第一部分是粒子先前的速度，代表粒子的状态；第二部分是粒子的“自我认知”部分，体现粒子的自我思考；第三部分是“社会”部分，体现粒子之间信息共享合作.

3 改进粒子群优化算法

Shi 和Eberhart 提出了粒子群优化算法［14］惯性权重线性递减的策略，对粒子群算法进行了修改，引入了惯性权重w.速度公式更改如下：

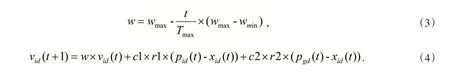
一定程度上优化了文献［1］粒子的寻优性能，但线性递减的惯性权重并不能如实的反映粒子复杂的搜索过程，寻到的最优解精度也不高，为了更进一步优化算法性能，文献［15］在文献［2］的基础上将惯性权重w 修改为

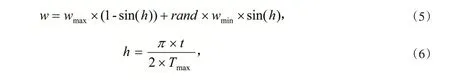
考虑了正弦函数的周期性，又添加了rand（0～1之间）随机数，来增加粒子搜索过程的随机性，但时间损耗较大.

为了进一步提高算法的寻优性能和收敛精度，将惯性权重w 调整为

4 实验与结果分析

4.1 测试函数

（1）Rastrigin函数：具有大量极值的多峰函数，其全局最优解和最优位置分别为

（2）Griewank函数：多峰函数，且其局部极小值均匀分布，全局最优解和最优位置分别为

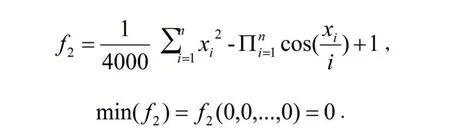
（3）Ackley函数：复杂的多峰函数，有无数个极小值点，其全局最优解和最优位置分别为

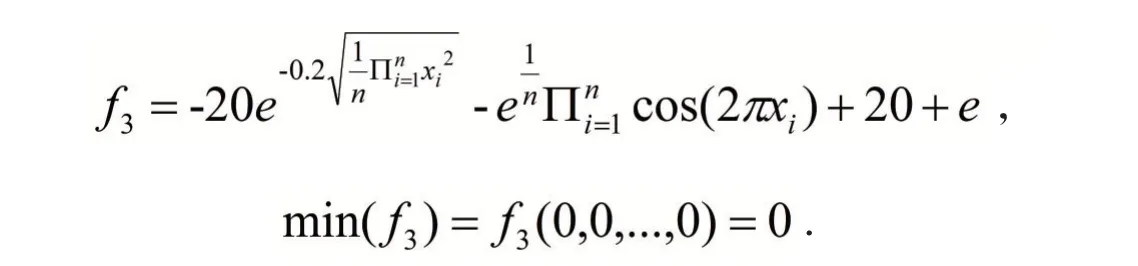
4.2 实验结果及分析

为了验证本文提出的XWPSO算法的有效性，采用XWPSO、PSO［1］、LPSO［14］、NXPSO［15］四种优化算法分别对Rastrigin、Griewank、Ackley三种经典函数进行优化，其中在PSO、LPSO、NXPSO优化算法中，2=2=1 cc，而在XWPSO 优化算法中05.2=2=1 cc，四种算法维度2=D，粒子数目40=N，搜索范围［-5，5］，惯性权重w 的变化范围［0.4，0.9］， 1r ， 2r 在［0，1］之间服从均匀分布的随机数，在Matble2016a环境中运行20次，实验结果如表1所示

表1 寻优结果对比

由表1可以看出，在对Rastrigin函数优化时，基本粒子群算法PSO最优值8.0912e-04，平均值为0.036055456；LPSO算法最优值1.9263e-05，平均值为0.038160856；NXPSO算法最优值1.4231e-05，平均值为8.0043445e-04.而改变惯性权重的XWPSO算法最优值6.6352e-07，平均值为2.52246296e-04，在Rastrigin函数极值的优化方面明显优于其他三种算法，更贴近函数最优解0，所以改进的粒子群优化算法较其他三种方法更优.同时对多峰函数Griewank、Ackley 的优化结果可以看到，从得到的最优值结果的平均值上来看，XWPSO算法也是明显优于其他算法的，从而验证了算法的有效性.

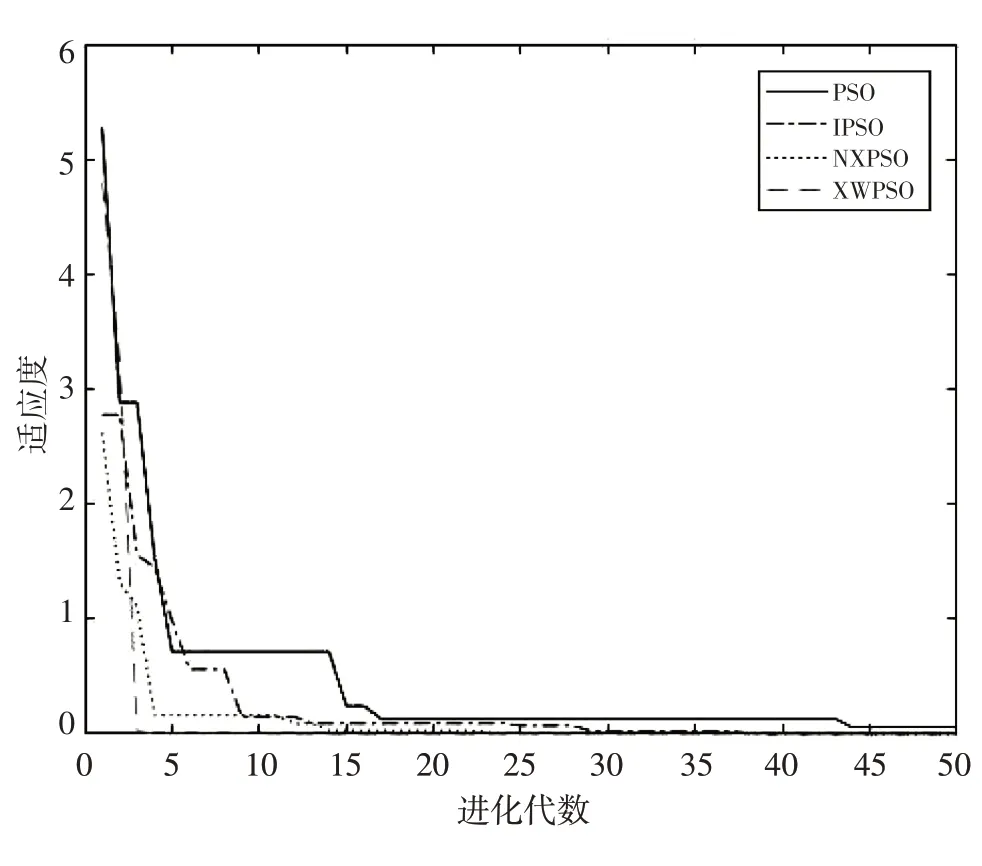
图1 Rastrigin函数在优化算法下的适应度曲线

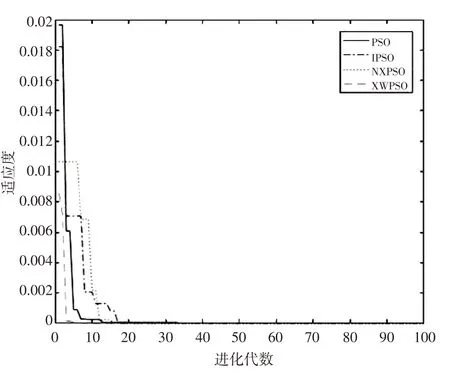
图2 Griewank函数在优化算法下的适应度曲线

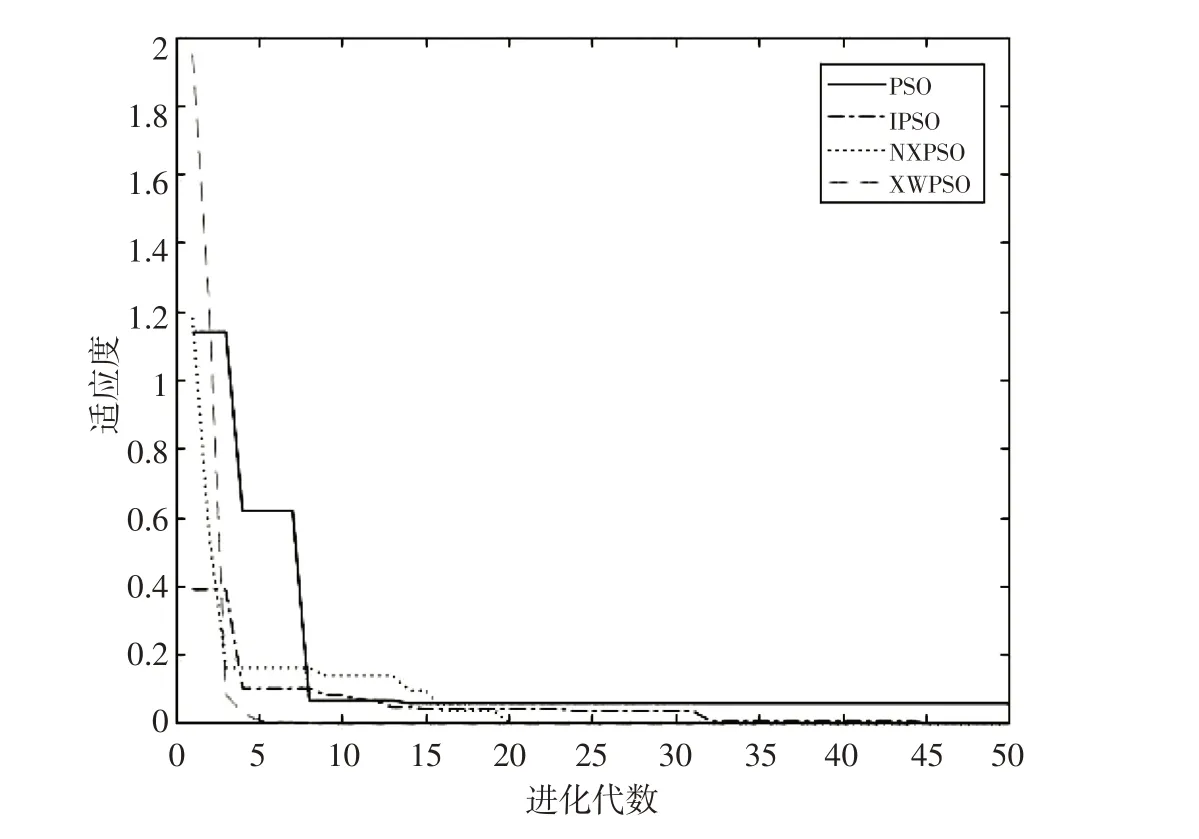
图3 Ackley函数在优化算法下的适应度曲线

Rastrigin、Griewank、Ackley 函数在PSO、LPSO、NXPSO、XWPSO 优化算法下的适应度曲线图如图1～3所示，XWPSO算法的适应度函数选用的是测试函数表达式本身，所以算法寻找到的适应度值就是要寻找的测试函数极值，从图中可看出，改进的粒子群算法较其他三种优化算法更早地收敛于函数的最优值，并且收敛精度也更高.在Rastrigin函数优化时，PSO算法在第17次迭代时趋于测试函数最优值，LPSO算法在第10次迭代时趋于测试函数最优值，NXPSO算法在第4次迭代时趋于测试函数最优值，XWPSO算法在第3次迭代时就趋于测试函数最优值；在Griewank函数优化时，PSO算法在第12次迭代时趋于测试函数最优值，LPSO算法在第18次迭代时趋于测试函数最优值，NXPSO算法在第11次迭代时趋于测试函数最优值，XWPSO算法在第3次迭代时趋于测试函数最优值；在Ackley函数优化时，PSO算法在第8次迭代时趋于测试函数最优值，LPSO算法在第4次迭代时趋于测试函数最优值，NXPSO 算法在第16 次迭代时趋于测试函数最优值，XWPSO 算法在第5次迭代时趋于测试函数最优值.

从实验结果可知，改进的粒子群优化算法XWPSO较其他几种优化算法具有较强的收敛性和收敛精度，尤其在Rastrigin、Ackley函数的优化效果更明显，从而也验证了XWPSO算法的有效性.

5 结语

本文应用的改进粒子群惯性权重的XWPSO在Shi和Eberhart提出的惯性权重线性递减的基础上添加了随迭代次数线性递增的调节因子p，使得改进之后的XWPSO在寻优能力和收敛精度上都有所提高，同时将XWPSO 算法与经典的PSO、LPSO、NXPSO 算法进行比较，该算法具有更快跳出局部极值，且收敛点更贴近函数最优解，与传统的PSO、LPSO、NXPSO算法相比较，XWPSO算法在测试函数维度2=n时寻优能力和收敛精度更高.